1. Introduction
Many authors have used the likelihood ratio to study the change-point problem (see [1] [2] ). Worsley, K.J. [3] gave exact approximate bounds for the null distributions of likelihood ratio statistics in two case of known and unknown variance. Simulation study results indicated that the approximation of his upper bound is very good for the small sample size, but the study does not support the case of large one. Koul and H.L, Qian. L. [4] studied the change-point by the maximum likelihood and random design. In the case of known variance, Jaruskova, D. [5] derived an asymptotic distribution of log-likelihood type ratio to detect a change-point from a known (or unknown) constant state to a trend state. Aue A., Horvath, L., Huskova, M. and Kokoszka, P. [1] studied the limit distribution of the trimmed version of the likelihood ratio, from which they received the test statistic to detect a change-point for the polynomial regressions. Researchers have used to take simulation studies on the various scenarios of the parameters of alternative hypothesis to find the power of a test. They have found that it depends on the sample size, variance of error and the behavior of the model function under alternative. For two phases’ regression, Lehmann, E.L. and Romano, J.P. [6] gave a formula to calculate the power of change-point through the noncentral F-distribution.
In this paper, the behavior of the model function under alternative is quantified by the roughness that is used to calculate the power of tests. The present paper is organized in the following way. In Section 2, we give a definition of the roughness of the model function and show some its properties; it is possible to take the limit of the roughness when the sequence of designs converges weakly to a limit design as well as designs are random. In Section 3, we present an explicit formula to calculate the noncentrality parameter of F-test in [6] through the roughness, and then the power of change-point test and some of its limits are considered.
2. The Roughness of the Model Function
To approximate the function 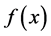 by a given system of functions
by a given system of functions 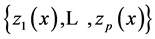 at the given points
at the given points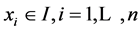 , we consider the model
, we consider the model
 (1)
(1)
 . (2)
. (2)
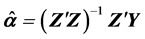 (3)
(3)
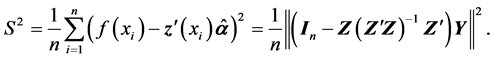 (4)
(4)
We call this value the roughness of the function 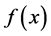 to the system of functions
to the system of functions 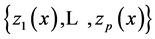 based on the design
based on the design 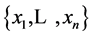 and denote it by
and denote it by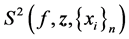 . In the case of a linear trend where
. In the case of a linear trend where 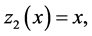
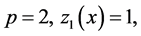
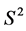 shows the nonlinearity of the curve
shows the nonlinearity of the curve 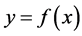 based on observations at
based on observations at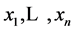 .
.
To study limits cases as well as other purposes, we call a distribution function ![]() whose support belongs to
whose support belongs to ![]() a (generalized) design on
a (generalized) design on![]() . A design
. A design ![]() is called to be adapted to a system of functions
is called to be adapted to a system of functions
![]() if its support belongs to
if its support belongs to ![]() so that the matrix
so that the matrix ![]() is invertible. In this paper, the used designs are assumed to be adapted to the system
is invertible. In this paper, the used designs are assumed to be adapted to the system ![]()
To continue, we will establish some assumptions:
(A2) Trend functions ![]() are linearly independent and continuous.
are linearly independent and continuous.
Now suppose that (A1) and (A2) hold, we approximate the function ![]() to
to ![]() in the equation:
in the equation:
![]() (5)
(5)
The estimate for the parameter vector ![]() that minimizes the weighted mean square error
that minimizes the weighted mean square error ![]() is
is
![]() (6)
(6)
where![]() . Hence, the estimate for the error of the model (5) is
. Hence, the estimate for the error of the model (5) is
![]() . (7)
. (7)
We also call this value the roughness of the function ![]() to the system of trend functions
to the system of trend functions ![]() based on the design
based on the design ![]() and denote it by
and denote it by ![]() It is easily seen that each discrete design is a generalized design, thus (3), (4) is a special case of (6), (7), respectively.
It is easily seen that each discrete design is a generalized design, thus (3), (4) is a special case of (6), (7), respectively.
According to [2] , to evaluate the roughness of the model function based on polynomial trend functions
![]() , by using the linear transformation of independent variables, instead of observing on the arbitrary
, by using the linear transformation of independent variables, instead of observing on the arbitrary
interval ![]() one can observe on the standard interval [0, 1]. Then, from now on, the model functions defined on [0, 1] are considered only.
one can observe on the standard interval [0, 1]. Then, from now on, the model functions defined on [0, 1] are considered only.
The following theorem in [7] shows the conditions for occurring the convergence of the estimated parameters and the roughness.
1) ![]()
2) ![]()
Now, we consider the model (1) where the observations ![]() are i.i.d. with the distribution function
are i.i.d. with the distribution function ![]() having support on
having support on ![]() The roughness of
The roughness of ![]() is calculated by (4), in which
is calculated by (4), in which ![]() is replaced by
is replaced by ![]()
![]() (8)
(8)
where
![]()
![]()
Theorem 2. Suppose that (A1) and (A2) hold for ![]() and
and
1) ![]() are independent random variables with the common distribution function
are independent random variables with the common distribution function ![]() having support on
having support on![]() ,
,
2) ![]()
3) The roughness ![]() is defined by (8).
is defined by (8).
Then
![]()
![]()
Let ![]() be the least-square estimate of
be the least-square estimate of ![]() bases on
bases on ![]() observations, we get
observations, we get
![]()
![]()
Because ![]() is a sequence of i.i.d. variables which have finite variance then by the strong law of large numbers,
is a sequence of i.i.d. variables which have finite variance then by the strong law of large numbers,
![]()
Then, according to the assumption 2),
![]()
which follows that elements of the matrix ![]() converge (a.s) to corresponding elements of the matrix
converge (a.s) to corresponding elements of the matrix ![]()
Similar arguments yield
![]()
Consequently, we obtain the limit
![]() (9)
(9)
Note that ![]() is not random and the roughness can be expressed by
is not random and the roughness can be expressed by
![]()
where
![]()
![]()
Because ![]() are i.i.d. and bounded then according to the central limit theorem,
are i.i.d. and bounded then according to the central limit theorem,
![]() (10)
(10)
Inasmuch as ![]() satisfies (9), it can be calculated by (6). Hence, the right side of (10) is
satisfies (9), it can be calculated by (6). Hence, the right side of (10) is ![]()
Again, according to the central limit theorem and (9),
![]()
Combining the above with the fact that ![]() we obtain
we obtain
![]()
This completes the proof of the theorem. ![]()
3. Applications to the Change-Point Test
Suppose that the model function is defined as:
![]() (11)
(11)
where ![]() are known functions,
are known functions, ![]() are unknown parameters. Observations
are unknown parameters. Observations ![]() belong to the closed interval
belong to the closed interval ![]() without the loss of generality, we can assume
without the loss of generality, we can assume ![]() some
some ![]() can be identical. Suppose that a change-point happened at a some time
can be identical. Suppose that a change-point happened at a some time ![]() the model is written:
the model is written:
![]() (12)
(12)
where ![]() is a sequence of i.i.d. variables
is a sequence of i.i.d. variables ![]() with the unknown common variance
with the unknown common variance![]() .
.
Let
![]()
Using matrix notations, the Equation (12) is written as
![]() (13)
(13)
We are interested in testing the hypothesis of structural stability against the alternative of a regime switch at a sometime ![]() that is
that is
![]() (14)
(14)
Let ![]() be known as it was studied in Bischoff and Miller [8] . In addition, we assume that the matrices
be known as it was studied in Bischoff and Miller [8] . In addition, we assume that the matrices ![]() have full rank:
have full rank: ![]() thence
thence ![]() From that, vector
From that, vector ![]() belongs to a
belongs to a ![]() -dimensional linear subspace
-dimensional linear subspace ![]() and the null hypothesis
and the null hypothesis ![]() to test that
to test that ![]() lies in a
lies in a ![]() dimensional subspace
dimensional subspace ![]() of
of ![]()
The least-squares estimate of ![]() under
under ![]() and
and ![]() under
under ![]() are
are![]() ,
,![]() and
and![]() , respectively. Let
, respectively. Let ![]() are the orthogonal projections of
are the orthogonal projections of ![]() onto
onto ![]() and
and ![]() then
then ![]() and
and ![]()
We already know that (see Lehmann, E.L. and Romano, J.P. [6] ): Under ![]() the statistics
the statistics
![]() (15)
(15)
will be distributed ![]() Thus, the test rejects the null hypothesis at level
Thus, the test rejects the null hypothesis at level ![]() if
if
![]() (16)
(16)
where ![]() is the
is the ![]() -critical value for
-critical value for ![]() a
a ![]() -distributed random variable with
-distributed random variable with ![]()
and ![]() degrees of freedom. According to [6] , by denoting
degrees of freedom. According to [6] , by denoting ![]() where
where ![]()
are orthogonal projections of ![]() onto
onto ![]() and
and ![]() respectively, then under
respectively, then under![]() , the statistic
, the statistic ![]() defined by (15) will be noncentral
defined by (15) will be noncentral ![]() -distribution with
-distribution with ![]() degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter
![]()
We note that ![]() and
and ![]() which implies that
which implies that
![]()
Now, we call ![]() and
and ![]() the signal-to-noise of the model (11) based on the design
the signal-to-noise of the model (11) based on the design ![]() and
and ![]() respectively.
respectively.
Theorem 3. If assumptions (A2), (A3) hold then the power of test (16) is defined by
![]() (17)
(17)
Remark. Theorem 3 shows an explicit formula of the power of change-point test. In the case of ![]() and
and![]() , if the model function
, if the model function ![]() is continuous segment, the shift of the slope between the first segment and the last one is
is continuous segment, the shift of the slope between the first segment and the last one is ![]() by Theorem 1 in [7] , the maximum roughness is obtained if the change-point
by Theorem 1 in [7] , the maximum roughness is obtained if the change-point ![]() is the midpoint of the observations. With the given common variance
is the midpoint of the observations. With the given common variance ![]() of the model, the maximum signal- to-noise
of the model, the maximum signal- to-noise ![]() is obtained at this change-point, thence from Theorem 3, the power is maximum. This fits results of simulation studies in [1] .
is obtained at this change-point, thence from Theorem 3, the power is maximum. This fits results of simulation studies in [1] .
To increase signal-to-noise ratio, we can decrease the noise or increase the roughness of the model function. When the variance ![]() is small, we can assert that if the model function has a change-point then this test will find it surely. On the other hand, if the variance is large, the test is poorly.
is small, we can assert that if the model function has a change-point then this test will find it surely. On the other hand, if the variance is large, the test is poorly.
With the sample size ![]() and design
and design ![]() if the variance
if the variance ![]() decreases to 0 then
decreases to 0 then ![]() increases to
increases to ![]() and if
and if ![]() increases to
increases to ![]() then
then ![]() decreases to 0. We have the following corollaries that show the relationship between power and the common variance and the roughness.
decreases to 0. We have the following corollaries that show the relationship between power and the common variance and the roughness.
Corollary 1. If the assumptions in Theorem 3 are satisfied then the following limits hold:
1) ![]()
2) ![]()
Limits of the powers are obtained by the following corollary.
Corollary 2. 1) With the same conditions as in Theorem 3, assume that ![]() for every
for every ![]() and some
and some ![]() then
then ![]()
2) Furthermore, if the model function ![]() and a sequence of designs
and a sequence of designs ![]() satisfies the conditions of Theorem 1, then
satisfies the conditions of Theorem 1, then ![]() as long as
as long as ![]()
Proof. First of all, it is easy to see that
![]()
where![]() ,
, ![]() are independent.
are independent.
Because ![]() then
then ![]()
Moreover, ![]() and
and ![]() then the last probability converges to 1 that yields 1).
then the last probability converges to 1 that yields 1).
Now, according to Theorem 1,
![]()
then 2) is implied straight from 1). ![]()