New Applications of the Noise Spectroscopy for Hydrogen Sensors ()
1. Introduction
For monitoring of the environment medium and controlling of the some technological processes producing noxious gases, selective and sensitive gas sensors are needed. Intensive search of new materials and new techniques for increasing semiconductor based gas sensors sensitivity is of great interest. It has been proposed as a main of extracting a more selective response from resistive gas sensors [1] [2] . It is well known that noise spectroscopy could be a useful tool for extracting information on the nature of the detected gas. As it is shown noise spectroscopy gives uncial possibility to analyze the composition of a number of different gases using only one sensor [1] . Potential peculiarities of the noise spectroscopy are analyzed in detail in [3] -[7] . Significant parameter to be considered for sensor development is the internal noise, because it is always a limiting factor for high-sensitivity applications. Therefore, noise spectroscopy and current fluctuation studies are usually employed in order to investigate the main noise sources as well as the overall noise behavior in different type sensors. A decrease of the feature thickness of sensitive layer t leads to an increase in the normalized 1/f noise density proportional to t−3 (see [8] [9] ). High sensitivity of spectral dependence of noise to carbon monoxide and ethyl alcohol vapors concentration of the sensors made on metal-porous Si-crystalline Si-metal sensors are observed [5] . It also observed the growth of the frequency index γ of the 1/f-noise Hooge formula: 0.5 in air, 0.85 for the air mixed with ethyl alcohol vapors; 1 for the air mixed 0.1% H2, and 1.3 for the air mixed with 0.4% CO [5] [10] . For describing noise fluctuation in gas sensors, several models are proposed: a model of adsorption-desorption noise in metal-oxide gas sensors using Langmuir’s and Wolkenstein theories [11] [12] , “Correlated number-mobility fluctuation model” [10] . For the bio-chemical sensors, we also have proposed trapping-detraping (adsorption-desorp- tion) and charge fluctuation models [13] [14] . Some new techniques of flicker noise spectroscopy that might improve the selectivity of thin layer semiconductor gas sensors are presented in [7] [15] . Static and noise characteristics of nanosized, porous and nanocomposite materials based hydrogen, alcohol and acetone gas sensors are analyzed in [16] -[18] .
In this paper, the results of the measured dependencies, theoretical simulation of the low-frequency noises behavior and influence of the sensitive layer thickness of the MgFeO4:Ti n-type porous semiconductor based hydrogen gas sensor are presented.
2. Samples Manufacturing
Corresponding raw materials (MgFe2O3 and Ti powders) are weighed according MgFe2O3 + 1 at.% Ti composition and mixed during 10 hours. Then we have thermal processing this composite at the temperature 800˚C - 1100˚C. The thermal processing sets free the humidity of the metal oxide raw material that facilitates uniformity of the powders mixture. Then, received composite is pressed under pressure 2000 N/cm2 as pallets with diameter 0.5 cm and the final thermal processing is carried out. Temperature and duration of the final thermal processing are chosen with a glance of composition for making solid phase ceramic medium. For avoiding mechanical tensions and flaws the temperature lowering is done very slowly (100˚C - 140˚C/hour). Thermal processing was executed using program-controlled vacuum furnace “Nabertherm HT 04/16”. For elimination of the surface defects finally processing samples are exposed to mechanical treatment, washed in turn in boiling toluol, alcohol and distilled water. From pallets, gas-sensitive samples with surface area 1 × 1 cm2 and several thicknesses are manufactured. Samples have n-type semiconductor conductivity. Then, sensitive layers are covered by the palladium catalytic nanosize particles using ion-plasmous deposition. After manufacturing of the gold inter-digital ohmic contacts, samples are fixed on the polycore substrate.
3. Experimental Setup and Measurements
Experimental arrangement for static and noise measurements is presented in Figure 1. Voltage from battery “ℇ”
![]()
Figure 1. Experimental arrangement for static characteristics and noise measurements.
is applied to sensor across load resistance R. By the low-noise amplifier (LNA) “SR 560” signal is amplified. Then Fourier analyze in the frequency range 2 - 300 Hz is done using dynamic signal analyzer “Handiscope 3”. Spectrum averaging number is equal to 200. Sensor, battery, gas cell and heating system are located in shielding box to protect from external electromagnetic influences. Noise spectral density (NSD) measured in air and in air + 0.5% hydrogen medium at the working temperature 300˚C and for the several thicknesses of the gas sensitive layer (SL) are presented in Figure 2 and Figure 3. NSD is measured in the frequency range up to 300 Hz as in the case the sensor working temperature ~300˚C flicker noise is effectively screening by the adsorption- desorption noise and high values of the thermal noise. In Figure 2 and Figure 3 t is the thickness of SL. For the optimal working regime sensor is heated using special heating system.
4. Results and Discussion
It is well known that MgFeO4 n-type porous semiconductor manufacturing process is accompanied by the intensive penetration of the oxygen molecules in the surface and subsurface region. Response of the metal oxide semiconductor based gas sensors is the result of the reactions carrying out in the surface and subsurface of SL. Having high value of electronegativity, at the normal conditions oxygen molecules are chemisorbed on the semiconductor surface interacted with the free electrons of n-type semiconductor and partially transformed to ,
, 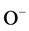 ,
, 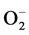 -ions. As noted in [19] , in the temperature range 150˚C - 400˚C the main part of those ions are
-ions. As noted in [19] , in the temperature range 150˚C - 400˚C the main part of those ions are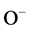 . As a result the depletion layer in the surface is formed. Gas molecules trigger a reaction with these oxygen ions according to following reaction:
. As a result the depletion layer in the surface is formed. Gas molecules trigger a reaction with these oxygen ions according to following reaction:
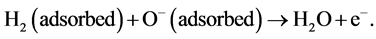 (1)
(1)
The additional electrons returned to semiconductor decrease resistivity of the SL.
It is well known that catalytic palladium granules has successful role for the gas sensitivity process. Especially ion-plasmous deposited catalytic palladium nanosize granules create active regions near their location and make simpler dissociation of the gas molecules. Palladium catalytic granules aid both leave of the electrons from
![]()
Figure 2. NSD measured in air at the several thicknesses of the gas sensitive layer: 1 - t = 37 nm, 2 - t = 41 nm, 3 - t = 45 nm.
![]()
Figure 3. NSD measured in air + 0.5% hydrogen at the several thicknesses of the gas sensitive layer: 1 - t = 37 nm, 2 - t = 41 nm, 3 - t = 45 nm.
the semiconductor volume region to the surface, deepen the depletion layer and more intensive transformation of the oxygen atoms to ions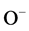 .
.
In the result, reaction (1) will take place more effectively and will increase concentration of the injected electrons in the semiconductor conduction band and therefore will deepen the modulation of the semiconductor resistivity.
For explaining and understanding the physical processes taking place in the sensor and responsible for the formation of low-frequency noise, the schematic picture and redox processes taking place in n-type semiconductor surface and subsurface SL are presented in Figure 4. As a result generated water molecules evaporate from sensitive surface. Part of the hydrogen molecules can also pass subsurface layer and plunge into volume part. Restored electrons from oxygen ions O− increase concentration of the free electrons (decrease resistance R) in the SL. In the other hand at the high working temperature (300˚C) mobility of the free electrons in the SL decreases. Modulation of the resistivity of SL conditioned by the fluctuation of the free electrons concentration and its mobility has random character and generated low-frequency noise. As the time constants involved in the detection of the H2 molecules via oxygenation with oxygen ions of the SL are relatively large it is expected that low-frequency noise is more critical than other types of noises.
For modeling of the noise spectral density  Hooge’s universal formula for macroscopically homogeneous materials and structures barely will be useful [20] :
Hooge’s universal formula for macroscopically homogeneous materials and structures barely will be useful [20] :
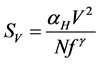 . (2)
. (2)
Here 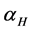 is the Hooge’s empirical parameter, V is the applied voltage, N is the number of the free carriers, f is the frequency, exponent
is the Hooge’s empirical parameter, V is the applied voltage, N is the number of the free carriers, f is the frequency, exponent 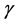 close to 1. At high temperatures (300˚C) only phonon scattering contributes to flicker noise and the other scattering mechanisms are reduced. Then the observed value of
close to 1. At high temperatures (300˚C) only phonon scattering contributes to flicker noise and the other scattering mechanisms are reduced. Then the observed value of 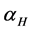 is as follows:
is as follows:
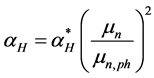 , (3)
, (3)
![]()
Figure 4. Electrochemical processes take place in the sensor. H2 molecules oxygenates with surface and subsurface oxygen ions O− (point line arrow) that gives back the initially accepted electrons to the metal oxide (full line arrow).
where ![]() is the true Hooge parameter,
is the true Hooge parameter, ![]() is the mobility if only phonon scattering exists [21] [22] . Note that at the electron lattice scattering on the acoustic phonons
is the mobility if only phonon scattering exists [21] [22] . Note that at the electron lattice scattering on the acoustic phonons ![]() and the mobility decreases at the high temperature and promotes to increase of NSD.
and the mobility decreases at the high temperature and promotes to increase of NSD.
As compared with clean air medium in the air + hydrogen medium NSD increases nearly in two orders. At the same time NSD decreases with the growth of the thicknesses of SL (see Figure 2 and Figure 3). Such behavior is conditioned by the reduction of the resistivity of SL and electron mobility. Number of the free carriers N depends on the thickness of sensitive layer t, mobility of electrons ![]() and resistivity R of the SL is as follows:
and resistivity R of the SL is as follows:
![]() , (4)
, (4)
where n is the concentration of free electrons, w and l are the width and length, ![]() is the specific resistance and
is the specific resistance and ![]() is the volume of SL. Then
is the volume of SL. Then
![]() . (5)
. (5)
It is interesting that NSD exponent ![]() is linearly decreasing depending on SL thickness (see Figure 5). It can thereby assume that Hooge parameter
is linearly decreasing depending on SL thickness (see Figure 5). It can thereby assume that Hooge parameter ![]() does not depend on SL thickness we receive that NSD inversely depend from t2. Note that such dependence of the NSD from structure thickness is also given in Langmuir theory [7] . In the other hand for the processes connected with the surface effects the Hooge parameter can increase with decreasing of the SL thickness
does not depend on SL thickness we receive that NSD inversely depend from t2. Note that such dependence of the NSD from structure thickness is also given in Langmuir theory [7] . In the other hand for the processes connected with the surface effects the Hooge parameter can increase with decreasing of the SL thickness ![]() [23] . Taking account this fact we can rewrite expression (5) in the form predicted in [8] [9] :
[23] . Taking account this fact we can rewrite expression (5) in the form predicted in [8] [9] :
![]() . (6)
. (6)
conditioned by the intensive influence of the Lorentzian component in the noise spectrum which is typical to adsorption-desorption noise [2] . Increasing of the thickness of SL brings to growth of the number of H2 molecules which pass surface and penetrate to the subsurface layer. Therefore adsorption-desorption process in the surface goes down. As thermal noise level decreases at the growth of the thickness it can have weak influence on the behavior of the exponent![]() .
.
Sensitivity of the sensor in air + 0.5% H2 increases with increasing of the thickness of SL. Sensitivity G calculated by the noise method ![]() several tenth times is higher, than by the resistive method
several tenth times is higher, than by the resistive method ![]() (
(![]() and
and![]() ,
, ![]() and
and ![]() are NSD and resistivities of the SL in the clean air and air + 0.5% H2 mediums, correspondingly, Figure 6). It gives successful possibilities for applications of the noise spectroscopy for detecting very small concentration of the hydrogen molecules. Estimation of the sensitivity by the noise method is considerably effective. Note that sensitivity of the hydrogen sensors made on crystalline silicon covered by the porous silicon layer (porosity 57%, air + 0.1% H2) with palladium contacts also gives high values of
are NSD and resistivities of the SL in the clean air and air + 0.5% H2 mediums, correspondingly, Figure 6). It gives successful possibilities for applications of the noise spectroscopy for detecting very small concentration of the hydrogen molecules. Estimation of the sensitivity by the noise method is considerably effective. Note that sensitivity of the hydrogen sensors made on crystalline silicon covered by the porous silicon layer (porosity 57%, air + 0.1% H2) with palladium contacts also gives high values of ![]() (~150) [16] . Comparison of the normalized NSD dependencies from SL thickness is presented in Figure 7. Theoretical curves are calculated using expression (5), (6) and experimental curve is plotted according to the data from Figure 3. Curves are very close. This fact proves accuracy usage of the Hooge’s formula (2) for describing gas sensors based on the porous MgFeO4:Ti metal oxide semiconductor. Note that experimental curve is more similar to dependence t−2. This fact hints that in the formation of the low-frequency noise together with surface effects subsurface (or volume) effects occur too.
(~150) [16] . Comparison of the normalized NSD dependencies from SL thickness is presented in Figure 7. Theoretical curves are calculated using expression (5), (6) and experimental curve is plotted according to the data from Figure 3. Curves are very close. This fact proves accuracy usage of the Hooge’s formula (2) for describing gas sensors based on the porous MgFeO4:Ti metal oxide semiconductor. Note that experimental curve is more similar to dependence t−2. This fact hints that in the formation of the low-frequency noise together with surface effects subsurface (or volume) effects occur too.
Finally, note that besides of the well-known applications, noise spectroscopy gives also the following additional possibilities:
· Definition of the unknown thickness of the sensitive layer (see, Equation (5));
![]()
Figure 5. Dependences of the noise parameter γ vs SL thickness in the air and air + 0.5% H2.
![]()
Figure 6. Dependences of G measured by the resistive and noise methods vs SL thickness.
![]()
Figure 7. Dependency of relative NSD vs SL thickness in the air + 0.5% H2, at T = 300˚C.
· Definition of the subsurface (or volume) role in the formation of the low-frequency noises by the shift of the dependency of NSD from sensitive layer thickness from t−3 law;
· Definition of the intensity of trapping-detrapping processes of the gas molecules by the change of noise exponent ![]() that is the result of the influence of Lorentzian spectrum on the NSD.
that is the result of the influence of Lorentzian spectrum on the NSD.