An Exact Formula for Estimation of Age-Specific Sensitivity for Screening Tests ()
1. Introduction
Screening of asymptomatic individuals for chronic diseases is a rapidly growing public health initiative. Early detection programs are aimed at detecting the disease in the stage when a disease is present without symptoms. For example, in breast cancer, there had been eight randomized screening trials demonstrating that mammography screening is beneficial in finding breast cancer at an earlier stage and consequently leads to a decrease in mortality among women of 50 - 65 years of age ([1] -[7] ).
One key element of these programs is a screening test. An important measure for the effectiveness of a screening test is sensitivity (b), the conditional probability of getting a positive screening test result given that one has the disease. Ideally it should be evaluated in the setting of natural history of disease model ([8] -[11] ). Often parameters like the sojourn time distribution in early stage of disease (pre-clinical state), transition probability from no disease state to early-stage disease state are needed to estimate the sensitivity.
These parameters are not directly observable and add to the complexity of the problem formulation and numerical computation of the sensitivity. Furthermore, the sensitivity can be age-dependent. For example in breast cancer the mammogram sensitivity in younger women is lower than that in older women [12] . The formulation for estimating age-dependent sensitivity becomes complex and does not always guarantee a numerical solution.
In this paper, we derive a formula that expresses age-dependent sensitivity in terms of probabilities that are directly observable in screening trials/programs and discuss the characteristics and generalization of this formula. We apply the formula to breast cancer screening trial (Health Insurance Plan) data to estimate the mammography sensitivity [1] .
2. Method: An Exact Expression for Age-Dependent Sensitivity 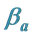
Consider the following health states in the natural history of disease progression:
· 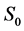 , the disease-free state, when the disease cannot be detected by any current early detection program;
, the disease-free state, when the disease cannot be detected by any current early detection program;
·  , the pre-clinical state, when the disease is detectable by an early detection program, but no symptoms are shown; and
, the pre-clinical state, when the disease is detectable by an early detection program, but no symptoms are shown; and
· 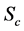 , the clinical state, when symptoms show.
, the clinical state, when symptoms show.
A progressive disease model assumes that the disease progresses in the direction  unless it is interrupted by a medical intervention. In the case of chronic progressive diseases, the goal of screening program in detecting the disease in
unless it is interrupted by a medical intervention. In the case of chronic progressive diseases, the goal of screening program in detecting the disease in . The age is denoted by a. Let
. The age is denoted by a. Let
·  be the sensitivity of the screening exam (i.e., the conditional probability that a disease is detected by the screening exam given disease is present) if the exam is taken at age a;
be the sensitivity of the screening exam (i.e., the conditional probability that a disease is detected by the screening exam given disease is present) if the exam is taken at age a;
· 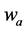 be the transition rate from
be the transition rate from 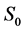 to
to 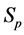 at age a;
at age a;
· 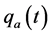 be the sojourn time distribution in
be the sojourn time distribution in 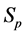 if the transition
if the transition  happens at age a; and
happens at age a; and
· 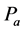 be the probability for case being in the pre-clinical state
be the probability for case being in the pre-clinical state 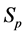 at age a, i.e. the proportion of people in
at age a, i.e. the proportion of people in 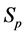 at age a in absence of screening examinations.
at age a in absence of screening examinations.
Note that![]() ,
, ![]() ,
, ![]() and
and ![]() are functions of age a, but to simplify notations, we use a in the subscripts. We also do this in part because our method will give estimates of
are functions of age a, but to simplify notations, we use a in the subscripts. We also do this in part because our method will give estimates of ![]() for discrete values of age a.
for discrete values of age a.
We now introduce two important probabilities that all the subsequent derivations are based upon. Suppose there are no screening examinations before age a, and a series of examinations are scheduled (but not necessarily taken) at times ![]() at ages
at ages![]() , with no examinations at other times. Consider a person of age a at time 0, taking
, with no examinations at other times. Consider a person of age a at time 0, taking ![]() examinations, at times
examinations, at times![]() . Let
. Let
· ![]() be the probability of entering
be the probability of entering ![]() before a, and still be in
before a, and still be in ![]() at age
at age ![]() if there has been no screening examinations; and
if there has been no screening examinations; and
· ![]() be the probability for a case undetected by the first
be the probability for a case undetected by the first ![]() exams and being detected in the pre-clinical state at the last examination at time
exams and being detected in the pre-clinical state at the last examination at time![]() .
.
The importance of ![]() is obvious as it is the probability that can be estimated directly from screening programs by taking proportions. The notion of
is obvious as it is the probability that can be estimated directly from screening programs by taking proportions. The notion of ![]() is more subtle, but it will facilitate derivations which will be shown later, especially when determining
is more subtle, but it will facilitate derivations which will be shown later, especially when determining ![]() and
and![]() .
.
Note that it is implied in the definition of T and X that by the time of the last examination, one would either be in ![]() or
or![]() , but not
, but not![]() . Thus if we were to use such definitions, we need to limit the cohort to only those who will still be in
. Thus if we were to use such definitions, we need to limit the cohort to only those who will still be in ![]() or
or ![]() by the last examination taken. In fact, the last examination would be at the same time when multiple
by the last examination taken. In fact, the last examination would be at the same time when multiple![]() ’s and
’s and![]() ’s appear in an equation together in all our derivations. Also note that
’s appear in an equation together in all our derivations. Also note that![]() .
.
We derive a formula for ![]() via a recursion based on the number of examinations. Consider a cohort of age
via a recursion based on the number of examinations. Consider a cohort of age ![]() at time 0, with examinations scheduled at times
at time 0, with examinations scheduled at times![]() . We have
. We have ![]() for
for![]() . n
. n![]() , or the probability of a case undetected at examination at time 0 but at
, or the probability of a case undetected at examination at time 0 but at![]() , involves the probability to enter
, involves the probability to enter ![]()
· before time 0 (or age a), go undetected at time 0, and stay in ![]() until getting detected
until getting detected![]() , which is
, which is![]() ; and
; and
· between time 0 and![]() , and stay in
, and stay in ![]() until at least
until at least![]() . This can be thought of as the difference between probability to be in
. This can be thought of as the difference between probability to be in ![]() at age
at age ![]() if there are no exams, or
if there are no exams, or![]() , and the probability to enter
, and the probability to enter ![]() before age a and stay in it until age
before age a and stay in it until age![]() , or
, or![]() . To be detected at
. To be detected at![]() , just multiply by
, just multiply by![]() , which gives
, which gives![]() .
.
Therefore,
![]()
Or,
![]() (1)
(1)
Similarly, for![]() , we need three terms, involving the probability to enter
, we need three terms, involving the probability to enter ![]() during the following times and stay in
during the following times and stay in ![]() until being detected at
until being detected at![]() :
:
· before age a and go undetected at times 0 and![]() , which is
, which is![]() ;
;
· between ages a and ![]() and go undetected at age
and go undetected at age![]() , which is
, which is![]() ; and
; and
· between ages ![]() and
and![]() , which is
, which is![]() .
.
Therefore,
![]()
From (1), we have ![]() and
and![]() , substituting both to the above formulation, we get
, substituting both to the above formulation, we get
![]()
which gives
![]() (2)
(2)
Observing (1) and (2), we arrive at our main result in this section:
Theorem 2.1.
![]() (3)
(3)
Therefore by writing out a few recursions, we are able to eliminate all ![]() terms and express the age- dependent
terms and express the age- dependent ![]() as a simple expression of the
as a simple expression of the ![]() terms, which are directly observable. A special case for application of Theorem 2.1 is when
terms, which are directly observable. A special case for application of Theorem 2.1 is when![]() . This implies a situation where repeated tests are performed on the same individual to measuring the sensitivity. For example, assume up to three repeated tests with the same sensitivity are performed at the same time, at three testing centers with same equipment. We label the testing centers as Center 1, Center 2 and Center 3.
. This implies a situation where repeated tests are performed on the same individual to measuring the sensitivity. For example, assume up to three repeated tests with the same sensitivity are performed at the same time, at three testing centers with same equipment. We label the testing centers as Center 1, Center 2 and Center 3.
Let ![]() be the probability of being detected at Center 1, regardless of what the results from Centers 2 and 3. Let
be the probability of being detected at Center 1, regardless of what the results from Centers 2 and 3. Let ![]() be the probability of being detected by Center 2, but not Center 1, regardless of the result from Center 3. This is equivalent to the probability of being detected by Center 3, but not Center 2, regardless of the result from Center 1. Lastly, let
be the probability of being detected by Center 2, but not Center 1, regardless of the result from Center 3. This is equivalent to the probability of being detected by Center 3, but not Center 2, regardless of the result from Center 1. Lastly, let ![]() be probability of being detected by Center 3, but not Center 1 or 2. The subtlety here is that
be probability of being detected by Center 3, but not Center 1 or 2. The subtlety here is that ![]() is not the probability of being detected by one center out the three, but just 1/3 of it, because we have ordered the centers beforehand. Then we have
is not the probability of being detected by one center out the three, but just 1/3 of it, because we have ordered the centers beforehand. Then we have
Corollary 2.2. When at least three repeated tests with the same sensitivity ![]() can be performed at the same time, we have
can be performed at the same time, we have
![]()
The result is achieved by simply taking limits ![]() and
and ![]() in the derivation for Theorem 2.1.
in the derivation for Theorem 2.1.
Theorem 2.1 is far from being intuitive, but corollary is easily verified, when we realize that when ![]() and
and![]() , there is
, there is![]() ,
, ![]() , and
, and![]() .
.
Advantage of Theorem 2.1. One main advantage of Theorem 2.1 is that it enables us to ignore the consideration for transition rate ![]() and sojourn time distribution
and sojourn time distribution ![]() in our set-up, which, even in the simplest cases, creates a complicated relationship. For example, consider the cohort of age 50, all getting their first screening exam. The probability of being detected, if we write it all out as an integral [13] , is
in our set-up, which, even in the simplest cases, creates a complicated relationship. For example, consider the cohort of age 50, all getting their first screening exam. The probability of being detected, if we write it all out as an integral [13] , is
![]()
where ![]() is the transition probability from
is the transition probability from ![]() to
to ![]() at age
at age ![]() and
and ![]() is the sojourn time distribution if the transition
is the sojourn time distribution if the transition ![]() happens at age
happens at age![]() . The interpretation of this expression is straight-forward: to be detected at age 50, the transition
. The interpretation of this expression is straight-forward: to be detected at age 50, the transition ![]() needs to happen at some age
needs to happen at some age ![]() before 50, therefore the first integral; and
before 50, therefore the first integral; and ![]() needs to last from age
needs to last from age ![]() to at least age 50, therefore the second integral.
to at least age 50, therefore the second integral.
Thus in just this one term, all the![]() ’s and
’s and![]() ’s for
’s for ![]() less than age 50 are involved, when we do not even know what type of distribution
less than age 50 are involved, when we do not even know what type of distribution ![]() is, which may vary for different
is, which may vary for different![]() ’s. This is just the simplest case—when there are multiple exams involved, the expressions for the probability of detection will involve several double integrals. One of the more rigorous approaches by Shen and Zelen ([10] ) uses such expressions to form likelihood function to find estimates for
’s. This is just the simplest case—when there are multiple exams involved, the expressions for the probability of detection will involve several double integrals. One of the more rigorous approaches by Shen and Zelen ([10] ) uses such expressions to form likelihood function to find estimates for![]() ,
, ![]() and
and![]() . But due to the complexity of such expressions, even when age-dependency is ignored, and
. But due to the complexity of such expressions, even when age-dependency is ignored, and ![]() is assumed to be exponential (so there are only three parameters to determine:
is assumed to be exponential (so there are only three parameters to determine:![]() ,
, ![]() and the parameter for the exponential
and the parameter for the exponential![]() ), there is no guarantee that a global maximum exists, or can be determined [11] .
), there is no guarantee that a global maximum exists, or can be determined [11] .
However Theorem 2.1 allows us to bypass ![]() and
and ![]() and find an expression for
and find an expression for ![]() in as an exact expression of
in as an exact expression of![]() ’s. This, of course, does not mean that the effects of
’s. This, of course, does not mean that the effects of ![]() on detection can be isolated from that of
on detection can be isolated from that of ![]() and
and![]() , but that the information of
, but that the information of ![]() and
and ![]() are already incorporated in the
are already incorporated in the![]() ’s. We also want to point out that the
’s. We also want to point out that the![]() ’s involved in Theorem 2.1 are naturally observable probabilities in the case of breast cancer screening (which is the main area of study for the authors): it is recommended that women to be screened either once every year, which gives terms
’s involved in Theorem 2.1 are naturally observable probabilities in the case of breast cancer screening (which is the main area of study for the authors): it is recommended that women to be screened either once every year, which gives terms![]() ,
, ![]() , or once every other year, which gives term
, or once every other year, which gives term![]() .
.
Another important advantage of Theorem 2.1 is that once (age-dependent) ![]() is determined, we will be able to determine age-dependent w and q with various approaches in a more exact manner. This we will explore in another paper.
is determined, we will be able to determine age-dependent w and q with various approaches in a more exact manner. This we will explore in another paper.
One limitation of the Theorem 2.1 is that it does not provide a way to apply the “interval cases”, or the cases that enter clinical stages between two scheduled screening exams. These cases, however, can be used later on to determine w and ![]() once
once ![]() is determined.
is determined.
3. Symmetry between X and T
An interesting mathematical result involves certain symmetry between X and T. We use the same setup as in the last section: suppose there are no examinations before age a, and a series of exams are scheduled (but not necessarily taken) at times ![]()
![]() at ages
at ages![]() , with no examinations at other times. Consider a person of age a at time
, with no examinations at other times. Consider a person of age a at time![]() , taking m examinations at times
, taking m examinations at times![]() . Recall that we let
. Recall that we let ![]() be the probability for the person to be undetected by all of the first
be the probability for the person to be undetected by all of the first ![]() exams and only detected to be in the pre-clinical stage at the last exam at time
exams and only detected to be in the pre-clinical stage at the last exam at time![]() .
.
Under the same set up, we introduce the new notation:
![]() (4)
(4)
where ![]() is the probability for someone to enter
is the probability for someone to enter ![]() before age
before age ![]() and still being in
and still being in ![]() at age
at age![]() , if there has not been any medical intervention. Thus
, if there has not been any medical intervention. Thus ![]() is the probability for such a patient being detected at examinations taken at times
is the probability for such a patient being detected at examinations taken at times![]() . This is a hypothetical probability that will facilitate our derivation.
. This is a hypothetical probability that will facilitate our derivation.
We also recall how we have defined![]() : let
: let ![]() be the probability for the person to be undetected by all of the first
be the probability for the person to be undetected by all of the first ![]() exams and only detected to be in the pre-clinical stage at the last examination at time
exams and only detected to be in the pre-clinical stage at the last examination at time![]() . So the onset of
. So the onset of ![]() can happen anytime before
can happen anytime before![]() , as compared to in the definition of
, as compared to in the definition of ![]() (and therefore
(and therefore![]() ), where the onset of
), where the onset of ![]() occurs before age
occurs before age![]() .
.
Recall we derived the following expressions in the last section (notice that![]() ):
):
![]()
or, after some reorganizing of the terms, and recognizing that![]() , we have
, we have
![]()
Therefore it is clear that there is a symmetric relationship between the T terms and the corresponding Y terms, in the case of 1, 2 and 3 examinations. The pattern of these expressions becomes more obvious in case of 4 examinations: (which will be proved along with the general case) to make it more obvious:
![]()
In the expression of ![]() in terms of the Y terms (and vice versa), the subscripts of Y terms go though all the eight subsets of
in terms of the Y terms (and vice versa), the subscripts of Y terms go though all the eight subsets of ![]() union 3, and the sign in front of the Y terms alternate according to the size of the subset. These facts turn out to be universal. We have:
union 3, and the sign in front of the Y terms alternate according to the size of the subset. These facts turn out to be universal. We have:
Theorem 3.1. For any![]() , there is
, there is
![]()
and
![]()
where S goes over all subsets of![]() , including the empty set, and
, including the empty set, and ![]() is the size of S.
is the size of S.
Proof. Because we will be applying the inclusion-exclusion principle later, to make the corresponding arguments, we revise the definition of the![]() ’s slightly. Assume a series of examinations are scheduled at times
’s slightly. Assume a series of examinations are scheduled at times ![]()
![]() at ages
at ages![]() ,
, ![]() ,
, ![]() , with no examinations at other times. However, assume that all the examinations are taken (again it is implied that one is still in either
, with no examinations at other times. However, assume that all the examinations are taken (again it is implied that one is still in either ![]() or
or ![]() by the time
by the time![]() , i.e., we limit to the cohort of such), and not all results are taken into consideration. Therefore even if
, i.e., we limit to the cohort of such), and not all results are taken into consideration. Therefore even if ![]() has been detected at time
has been detected at time ![]()
![]() , all the subsequent examinations will still be taken. Let
, all the subsequent examinations will still be taken. Let ![]() be the probability for the person be the probability for an individual undetected by the examinations at times
be the probability for the person be the probability for an individual undetected by the examinations at times![]() , and detected in
, and detected in ![]() at exam
at exam![]() , regardless of what happens at other examinations. Although the definition for
, regardless of what happens at other examinations. Although the definition for![]() ’s has changed, the numerical expression of
’s has changed, the numerical expression of![]() ’s are the same as before.
’s are the same as before.
Let
· ![]()
![]() be the event of being detected at
be the event of being detected at ![]() but undetected at
but undetected at![]() ;
;
· ![]() be the event of being detected at
be the event of being detected at![]() ;
;
· ![]() be the event of being detected at all exams at
be the event of being detected at all exams at![]() .
.
Therefore we have
![]()
and ![]() (which is also equal to
(which is also equal to![]() ), while the size of the right-hand-side would be
), while the size of the right-hand-side would be
![]() , since A and each Ci are mutually exclusive events. We also have
, since A and each Ci are mutually exclusive events. We also have![]() .
.
By inclusion-exclusion principle [14] ,
![]()
But ![]() is simply
is simply![]() , therefore we have
, therefore we have
![]()
Or,![]() .
.
The second expression can be proved in a similar manner. With the same set up as the above, let
· ![]()
![]() be the event of being detected by two examinations at
be the event of being detected by two examinations at ![]() and at
and at![]() ;
;
· ![]() be the event of being undetected by every examination taken at
be the event of being undetected by every examination taken at![]() , but detected at
, but detected at![]() .
.
Recall that ![]() is the subset of all those detected at
is the subset of all those detected at![]() , then
, then
![]()
and![]() . While this time the size of the right-hand-size is
. While this time the size of the right-hand-size is![]() , since B and each
, since B and each ![]() are mutually exclusive events. We also have
are mutually exclusive events. We also have![]() .
.
Again by inclusion-exclusion principle,
![]()
However ![]() is simply
is simply![]() , therefore we have
, therefore we have
![]()
Or,![]() .
.
Corollary 3.2. There are infinitely many expressions of age-specificity in terms of![]() .
.
Proof. This is because each ![]()
![]() can be expressed as
can be expressed as
![]()
where ![]() is any subset of
is any subset of ![]() that contains
that contains![]() , and
, and ![]() means
means ![]() without
without![]() . For example,
. For example,
we saw in the last section that![]() , and it is also equal to
, and it is also equal to![]() , etc.
, etc.
Each ![]() can be expressed in terms of
can be expressed in terms of![]() ’s.
’s. ![]()
Given expressions like Theorem 3.1, the proof for Theorem 2.1 is not as straightforward. However the purpose of that proof was to relate some of the traditional considerations and reasoning’s to our new notions. This will be useful when evaluating important parameters such as age-dependent disease transition probabilities and sojourn time distribution.
4. An Example
We illustrate the proposed method using the data from the Health Insurance Plan Project, or HIP data [1] . HIP is a randomized screening trial of mammography screening vs. no screening for the women who did not have previous mammography. Even though HIP is a large-scale screening trial, because breast cancer incidence rate is relatively low, we do not have sufficient number of screen-detected and interval cases to readily estimate age-specific![]() . Thus for an illustration of the Theorem 2.1, we group all the women together as one age group, and assume that all patients had the same age at the initial examination. Because the cohort is required to have annual check-ups, we set
. Thus for an illustration of the Theorem 2.1, we group all the women together as one age group, and assume that all patients had the same age at the initial examination. Because the cohort is required to have annual check-ups, we set ![]() and
and ![]() in the Theorem 2.1, and get
in the Theorem 2.1, and get
![]()
To calculate, saying![]() , we simply use the ratio between the number of cases detected at the first annual examination after the initial examination and all the cases who had taken both examinations. Using the HIP data, we get
, we simply use the ratio between the number of cases detected at the first annual examination after the initial examination and all the cases who had taken both examinations. Using the HIP data, we get
![]()
Note that this estimate is essentially identical to Shen and Zelen’s published estimate of 0.7 ([10] [11] ) based on the maximum likelihood method, but is computationally trivial.
Acknowledgements
This work was supported by grants 1RC CA 146496-01 and 1R01 CA16430 from the National Cancer Institute/National Institute of Health.
NOTES
*Corresponding author.