1. Introduction
Above the Curie temperature TC, colossal magnetoresistance (CMR) perovskite manganites behave paramagnetic insulating state. As the temperature is decreased below TC, they become ferromagnetic metals. It is shown that the ferromagnetic clusters are formed and extracted as decreasing temperature below TC. The existence of ferromagnetic clusters above TC [1] as well as inhomogeneity and phase separation [2] suggests that ferro-magnetic long-range order may be established by percolation of ferromagnetic regions as the temperature is lowered. Such magnetic inhomogeneities in the spin systems may be a result in a reduced local effective topological dimensionality [3] , thereby leading to different critical behaviors. Hence, the critical properties of the paramagnetic-fer- romagnetic (PM-FM) phase transitions in manganites pose an important fundamental problem. On the other hand, the vast variability of competing mechanisms, which may influence the magnetic ordering, may also yield other types of paramagnetic-ferromagnetic transitions for different systems in this class of materials. Experimental studies [4] -[6] of critical behavior of manganites near the PM-FM phase transition by using a variety of techniques have yielded a wide range of values for the critical exponent of b. The values range from about 0.3 - 0.5, which embrace mean-field (b = 0.5), three-dimensional (3D) isotropic nearest-neighbor Heisenberg (b = 0.365) and 3D Ising (b = 0.325) estimates. Static dc-magnetization measurements [4] -[7] , in addition to b, also yield the critical parameters g and d for initial susceptibility c(T) and critical isotherm M(T, H), respectively. However, they may fail to determine a unique universality class for the phase transition of these manganites. The very low values of b = 0.095 for LaMnO3 [5] and 0.147 for La0.7Ca0.3MnO3 [6] obtained from static magnetization measurements suggest that the PM-FM transition in these compounds is first-order transition. Further, a first-order PM-FM phase transition has been reported [8] for La0.7Ca0.3MnO3 based on the sign of the slope of the isotherm plots, (H/M)1/g vs. M1/b (g = 1 and b = 0.5 or g = 1.336 and b = 0.365). Interestingly, a continuous transition has been reported [7] for La0.8Ca0.2MnO3. Recently, a critical point has been identified [9] in the La1-xCaxMnO3 phase diagram at x = 0.4, thus marking a boundary between first- and second-order phase transitions. La0.7Sr0.3MnO3, a typical perovskite, has generated much interest in recent work. It has a ferromagnetic transition near 360 K [10] , which is the highest TC among perovskite manganites having the same Mn3+/Mn4+ ratio of 7/3. The critical parameters of maganites materials have been reported in a number of publications. It is interesting that the temperature can be shifted to room temperature for applications.
According to the Curie-Weiss law for ferromagnetism, the large magnetic entropy change, ΔSM(T,H), is expected at the Curie temperature TC and has high values for materials having large effective magnetic moment [11] . Since 1996, there have been numerous reports of exceptionally large magnetocaloric effects in perovskite manganese oxides [12] -[16] . In this paper, we report the critical parameters b, g and d determined from the Arrott plots, Arrott plots modified and magnetocaloric effects of the La5/8Ca3/8Mn0.975Pd0.025O3 compound by analyzing the magnetization curves.
2. Experiments
The sample was fabricated by the sol-gel method. The original chemical substance are La(NO3)2, Ca(NO3)2, Mn(NO3)2 and PdCl2 with the pure of more than 99.99%. The sample had been heated at 980˚C for 3 hours. After that it had been sintered at 1050˚C for 4 hours in air. Sample was checked and confirmed by X-ray diffraction. The results show that the sample was quality with structure of orthorhombic. The magnetic measurements were carried out on the PPMS-6000.
3. Results and Discussion
Figure 1 shows the temperature dependence of magnetisation of the sample measured in the applied field of 100 Oe using zero field cooled and field cooled mode. The ferro-paramagnetic transition temperature is TC = 252.7 K, defined from derivative the M(T) curve as temperature. The sample behaves the second-order-phase transition. It also behaves a large of the range of temperature. This is a typical behavior of the samples fabricated by sol-gel
![]()
Figure 1. The temperature dependence of the magnetisation of the La5/8Ca3/8Mn0.975Pd0.025O3 sample.
method. The range of the wide of transition as well the difference between the zero-field cooled and filed cooled in the range of low temperature does not seems to reflect the chemical disorder but seems due to the disorder in magnetism. It may be in a result of phase separation phenomenal [15] .
Figure 2 shows the magnetic field dependence of magnetization at different temperatures. It can be seen that at low temperatures, far from TC, the value of magnetisation of the sample is not saturated. To understand clearly the interaction between the samples, we have built the Arrot plots. The transition temperature, of cause, is not shown from the shape of the curves event thought near the phase transition. So we have had to build the Arot plots modified by using the critical exponents.
In the range of the ferro-paramagnetic transition temperature, the scaling law was used for the saturate magnetisation and susceptibility and given by [16] [17] . The critical parameters β and γ, are inferred by using
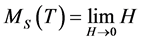 in the temperatures of T < TC. The susceptibility is defined by the equation
in the temperatures of T < TC. The susceptibility is defined by the equation  in
in
the range of temperatures T > TC. At the ferro-magnetic transition temperature, the applied field dependence of
the susceptibility is given by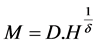 , where the critical parameter δ = 1 + γ/β. The value of δ can be found
, where the critical parameter δ = 1 + γ/β. The value of δ can be found
from the log(M) curves versus log(H) at TC. By the extrapolating the Arot plots, we have gained the saturate magnetisasion and susceptibility as shown in the Figure 3. The critical parameters of the sample are defined of b = 0.48633, g = 1.1826 and δ = 3.431682. This implies that both mean-field and Heisenberg model are not applied for those samples. As mentioned above, the samples are complicated phase in physic so this term can be
![]()
Figure 2. The isotherm curves of the La5/8Ca3/8Mn0.975 Pd0.025O3 sample at different temperatures.
![]()
Figure 3. The temperature dependence of the saturate magnetisation and susceptibility of the La5/8Ca3/8Mn0.975 Pd0.025O3 sample.
explained by a point of view of phase separation. The critical parameters defined are between the mean-filed and Heisenberg model. This suggests that the sample seems not to be single phase but at least two phases, which should obey mean-field and Heisenberg model.
The thermo-magnetisation measurements show the transition temperature TC = 252.7 K. However, it is relative based on the derivative of the curve M(T) as T. This value was defined at the peak of the derivative curve. At this temperature, the variety of magnetisation as temperature is the strongest. Base on the obtained results, we have calculated and defined the ferro-magnetic transition temperature of the sample TC = 247.79 K. This is mean value after calculating both temperature regions above and below TC. It is much different to the value defined by the magnetisation curve. However, this value is more exactly because it is defined in the region of phase transition. It behaves the nature of the transition process in the sample.
The Arot plots modified were built using the critical parameters. The result is shown in the Figure 4. The Arot plots modified show the difference above the shape of the between two regions, above and below TC, which was defined to be TC = 247.79 K by analyzing the data of saturate magnetisation and susceptibility. This shows that there is a strongest change of magnetic order of the sample at 247.9 K.
The magnetocaloric phenomena was investigated using the applied field dependence of the magnerisation, M(H), at different temperatures. The result is displayed in the Figure 5. The magnetocaloric curves calculated for the applied fields of 0.5 T up to 6.0 T. As can be seen from Figure 5, the peaks of those curves shift to the higher temperature in higher applied field. In the low field, magnetocaloric shift to the ferro-paramagnetic transition temperature, TC = 247.79 K. This can be understood that the magnetocaloric phenomenon is strongest at
![]()
Figure 4. The Arrot modified of La5/8Ca3/8Mn0.975Pd0.025O3.
![]()
Figure 5. The CME in the La5/8Ca3/8Mn0.975Pd0.025O3 sample in the difference applied fields.
the phase transition temperature related to the applied field for the thermo-magnetisation measurements. The shifting of the peaks due to the transition phase temperature is shifted to higher in high applied field. Approximate of 5 J/Kg∙K is the maximum value of magnetocaloric gained in the applied field of 6 T. Despite of small but it is close to room temperature. It is interesting that the magnetocaloric phenomenon broad over temperature region. It reduces sharply as increasing temperature higher TC whereas it reduces more slowly in the temperature lowers TC. This can be explained that in the temperature higher TC, the materials is paramagnetic and it is ferromagnetic in the lowers TC.
Phase separation of the materials can affect the positive effects at TC such as magnetoresistance or magnetocaloric. For the magnetoresistance, phase separation plays a role in the temperature region. It enhances the low- field magnetoresistance especially in low temperatures, far from TC. However, the magnetocaloric is not enhanced in low temperatures. This is a challenge for application.
4. Conclusion
The critical parameters have been studied. The results show b = 0.48633, g = 1.1826 and δ = 3.431682. This means that the transition model of the sample is between the mean-field and the Heisenberg mode. The thermomagnetic properties were investigated. The results show that Pd substituted for Mn in the materials reduces the ferro-paramagnetic transition temperature as well as magnetocaloric. However, the region of temperature having magnetocaloric is broadened to the lower transition temperature.
Acknowledgements
This work was supported by the National Foundation for Science & Technology Developments (NAFOSTED), Vietnam, project code: 103.02-2010.28. We thank Dr. Dao Nguyen Hoai Nam working for Institute of Materials Science of his measurements as well as his comments.