Methodology for Evaluating and Monitoring of Waterworks Performance Efficiency—Part 2: Test of Filterability ()
1. Introduction
One of the main objectives of the mathematical models of filtration is to calculate the length of the filtration cycle. This is based on the selected design parameters of the filter and its operational condition. The aim is that the calculated length of filtration cycle corresponds to the results obtained from constructed filters. The duration of the filtration cycle depends on both the concentration of pollutants in the filtrate and also the pressure head loss generated by the filtration process.
The deep-bed filtration process is considerably more complex than other separation processes. This is because deep-bed filtration is a cyclic process whereas gravity separation process such as sedimentation is a continuous process. Therefore, filter beds must be regularly regenerated. This means that filtration efficiency is a time dependent variable.
The equipment forming part of the filtration plant does not depend on the expected length of the filtration cycle. The waterworks operation is adjusted to accommodate different lengths of the filtration cycles. Depending on whichever is achieved first the length of the filtration cycle is governed by
Ø penetration of the cation of destabilisation agent into the filtrate,
Ø maximum design head loss,
Ø maximum permissible sub-atmospheric pressure in the filter bed,
Ø recommended maximum length of the filtration cycle (usually 72 hours).
When the expected length of the filtration cycle is not achieved the waterworks production capacity is usually not affected. However, this detrimentally affects the economy of the waterworks operation due to increased consumption in energy and water.
The deep-bed filtration efficiency is derived in a quantifiable manner from the properties of the filtration media and properties of the suspension to be filtered. These properties cannot act in isolation of each other. In addition, filtration is influenced by its operational conditions, i.e. by the filtration velocity, operating pressure conditions and filter backwashing. The properties of flocculent suspension which make it particularly suitable for separation by sedimentation are not necessarily those which make the suspension suitable for deep-bed filtration. Unsuitable properties of suspension result in shortened filtration cycles. One of the common challenges in waterworks operation is to establish operational interventions which are required to extend the filtration cycle. This challenge results from not knowing the physical-chemical properties of the suspension with respect to filtration, i.e. the filterability of suspension.
Filterability of suspension is defined as the capability of suspension to be intercepted in a layer of filtration media. The term filterability covers the whole complex of properties of suspension which enables its interception in the filter bed. It is considered to be synonymous with efficiency of filtration. The efficiency of filtration is not expressed only by the quality of the filtrate. In contrast to sedimentation, the efficiency of filtration is not the only parameter by which the filtration process is evaluated. Other parameters which must also be considered are filtration velocity and pressure loss generated during filtration. Both represent an economic criterion of filtration. Other variables influenced by filtration velocity are [1] [2] :
Ø the rate at which suspension is intercepted in the filter bed,
Ø the total quantity of intercepted suspension,
Ø the total volume of filtrate produced,
Ø the length of the filtration cycle,
Ø the rate of increase in pressure loss.
The properties of suspension are the governing factors which provide data for filter design. Filter design should be such that all factors affecting the length of the filtration cycle should reach their limits at the same time. This means that for different properties of suspension different design parameters are required with respect to:
Ø granularity of the filter bed,
Ø height of filter bed,
Ø head loss,
Ø filtration velocity.
The efficiency of filtration is not constant. It is determined by the initial conditions of filtration i.e. granularity of filtration media, porosity of filter bed, filtration velocity, physical-chemical properties of water and suspension to be filtered and also by the specific volume of retained suspension. An important design constraint of filtration is the development of sub-atmospheric pressure in the filter bed. When this condition develops in the filter bed, the gas dissolved in the water is liberated and accumulated in the voids of the filter bed. The accumulation of gas reduces the sludge holding capacity of the bed and increases the rate of pressure loss. In addition, the air bubbles which escape from the filter bed increase the penetration of suspension into the filtrate.
The course of filtration is not only influenced by the design parameters of filtration but also by the properties of the water and the suspension being filtered. The commencing operational conditions of the filter are very significant. The quantity of suspension which was intercepted and not removed from the filter bed during backwashing is a major factor. This implies that the geometry of filters, backwashing procedures and the velocity of both air scour and backwash water influence the efficiency of backwashing and hence affect the filtration efficiency most significantly.
The properties of flocculent suspension with respect to filtration efficiency are determined by the test of filterability. The proposed test of filterability is carried out with a flow through a thin filtration layer. The principles of the test of filterability are based on the concept of the mechanistic model of filtration [1] [3] - [5] . The results obtained are evaluated by the mathematical model of this concept which is reviewed in this paper.
The equations in most of the models of filtration are derived from measured data especially from those linked to the influence of filtration velocity and grain size (granularity of media) [6] - [10] . In these models it is difficult to distinguish the influence of the quality water being filtered from the design parameters. In contrast, the equations in the mathematical model of mechanistic conception of filtration are derived from the basic theory of filtration. This permits to distinguish the influence of water quality from other influences.
Even though the mechanistic model of filtration was developed a long time ago it was not published in an English journal and therefore remains unknown to most of the water purification design engineers worldwide. This paper aims to rectify this shortcoming.
2. Mathematical Formulation of the Mechanistic Model of Filtration
The basic equations for the deep-bed filtration were developed by Iwasaki’s [11]
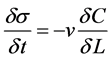 (1)
(1)
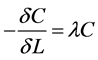 (2)
(2)
where: l: coefficient of filtration efficiency,
C: volumetric concentration of suspension,
L: height of filter bed,
v: filtration velocity,
t: time,
σ: specific volume of intercepted suspension.
The first equation (Equation (1)) shows that the decrease in the volume of suspended matter caused by the flow of water through an elementary filtration layer equals the increment by which the volume of intercepted matters increases in that layer over the same time. The second equation (Equation (2)) is based on the assumption that the decrease in the volumetric concentration of suspended matter caused by the flow through an elementary filtration layer is proportional to its instantaneous concentration prior to entering the layer. The application of the second equation is not as unquestionable as the first equation. This is not the only method of expressing the sought dependencies even though it is the most often used.
Determination of dependence λ = f(σ) is one of the most difficult to derive in any mathematical models of the filtration process.
The mathematical model of the mechanistic conception of filtration is developed from Equation (1). It incorporates a system of equations used to calculate the input data needed for calculating the coefficient of filtration efficiency λ. Furthermore, this system of equations permits development of a computer programme for the determination of the filtration efficiency, i.e. the filterability of suspension.
The mechanistic model of filtration is based on the assumption that the instantaneous value of the coefficient λ is dependent on the resultant of the adhesion and the hydrodynamic forces, the magnitude of which is dependent on the specific volume of intercepted suspension [2] [3] [5] . The adhesion forces enable interception of suspension on the surface of media grains and then on the surface of already retained suspension. They are proportional to the free surface area of grains covered with intercepted suspension. The hydrodynamic forces prevent interception of suspension and are proportional to the shear stress. These assumptions are expressed by the following equation
 (3)
(3)
where: a: specific surface area of grains as increased by the cover formed by the intercepted aggregates,
s: specific volume of intercepted suspension,
t: shear stress,
f1, f2: functions of specific volume of retained suspension.
The first function is expressed by the following relationship
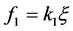 (3a)
(3a)
where: k1: coefficient expressing properties of suspension being filtered and filtration media,
ξ: coefficient determining increase of grain surface by intercepted suspension ξ = f(s).
The following relationship was developed for ξ
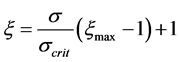 (3b)
(3b)
where: scrit: the value at which media grain is covered with a layer of suspension the thickness of which equals the characteristic dimension of intercepted aggregates dA. The scrit is defined as the value of s at which coefficient λ reaches its maximum value. The value scrit corresponds to the value lmax.
ξmax: for s ³ scrit is ξ = ξmax.
At scrit the charge ratio changes when further suspension is retained. Up to scrit the suspension is retained on the surface of media grain and at the higher s values suspension is retained on the layer of aggregates already retained on the grain.
The second function is obtained by substituting shear stress with hydraulic gradient and hydraulic radius and introducing boundary conditions
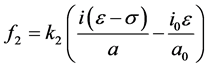 (3c)
(3c)
where: k2: coefficient expressing properties of suspension being filtered,
ε: porosity of clean filter media,
i: hydraulic gradient,
index 0: initial conditions.
By combining Equations (3) to (3c) the basic equation for the coefficient of filtration efficiency λ becomes
 (4)
(4)
As already mentioned in the foregoing the coefficient of filtration efficiency l is not constant. It is assumed that its instantaneous value depends on the resultant of adhesive and hydrodynamic forces.
The specific surface area of grains covered by a layer of intercepted suspension having a thickness of Δd/2 is expressed as follows
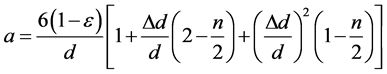 (5)
(5)
where a: specific surface area of grains covered by a layer of intercepted suspension,
d: diameter of the grain of the filtration media,
Dd: enlargement of media grain diameter covered with a layer of intercepted aggregates,
n: number of contacts of a grain with neighbouring grains which depends on the porosity of the filtration layer.
For the calculation of the above equation it is necessary to know the relationship between the enlargement of media grain d by a layer of aggregates Dd and the specific volume of intercepted suspension (s)
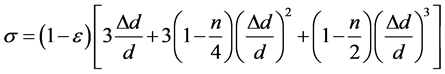 (6a)
(6a)
The scrit is defined as the value of s at which coefficient l has maximum value. It is calculated as follows
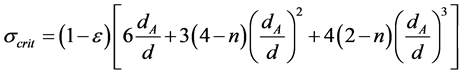 (6b)
(6b)
where dA: characteristic dimension of the aggregates.
Equation (6a) is based on the assumption that covering of media grains takes place in a layer of equidistant surfaces.
Deb [12] derived the following relationship for the number of contacts n between spherical grains and porosity of a clean filter bed
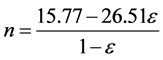 (7)
(7)
In the above equations the surface area of media grains a and the hydraulic gradient i are relatively complicated functions of s. However, these functions do not include coefficients which would express properties of aggregates.
For the calculation of hydraulic gradient i it is useful to calculate the ratio of the hydraulic gradient at a condition of clogging and a hydraulic gradient at the same flow velocity of water through a clean bed i0. For the equidistant coverage of media grain the following equation can be derived
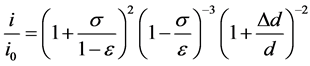 (8)
(8)
The hydraulic gradient at a flow velocity of clean water through a clean filter bed is calculated according to the modified Kozeny’s equation [13]
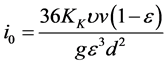 (9)
(9)
where: i: hydraulic gradient at the flow of water through the filter bed under the attained conditions of clogging,
i0: hydraulic gradient at the flow of water through a clean filter bed,
KK: Kozeny’s constant (for sand KK = 5),
v: flow velocity,
n: viscosity of water,
g: gravity constant.
For the simplification of calculations the cubed item in Equation (6a) can be eliminated and after solving the equation and substituting it into Equation (5), the combined Equations (5) and (6) become
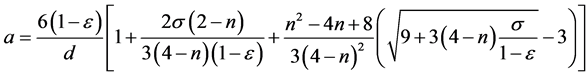 (10)
(10)
Based on the range of s values the difference in the results varies between 0% - 6%.
Equation (8) can be simplified by using its version developed by Mintz [14] who replaced the exponent-3 with a general exponent and calculated its value by adjusting the computation based on a condition that the sum of the squared errors against combined Equations (6a) and (8) is minimal. The Equation (8) as modified by Mintz [14] is
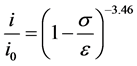 (11)
(11)
The intercepted suspension is compressed during the filtration cycle. Dependence of its volume on time of deposition in the filter bed is expressed by the following relationship
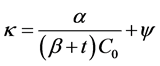 (12)
(12)
where: t: time,
C0: mass concentration of water entering the filter,
α, β, ψ: further coefficients defining properties of aggregates.
Generally, the properties of the aggregates are characterised by the following parameters: k1, k2, xmax, dA, α, β, ψ. Their values define their influence in the basic equations and consequently also on the assumed properties of the aggregates.
Parameters dA is derived from Equation 6(b) for the calculation of the value scrit which is dependent on the thickness of a layer of retained aggregates and the diameter of the media grain. The value of dA equals the thickness of a layer at which the highest efficiency of filtration is achieved. The corresponding s value is marked scrit. The value of scrit can be established from the function l = f(s) and by solving Equation (6b) to calculate the value of dA. Should the only influence determining the efficiency of the detainment of the aggregates be the surface area of media grains then the highest efficiency of detainment would occur at the beginning of the filtration cycle and decrease with the progressing duration of the filtration cycle. This action has no peak. The same applies to the action of tangential forces. During the filtration cycle the s value increases, the porosity decreases and consequently the tangential forces increase. However, improving efficiency of filtration at the beginning of the filtration cycle has been ascribed to enlargement of the specific surface area of media grains ξ by retained aggregates. Such enlargement ends when the surface area of the media grains is covered with a layer the thickness of which equals the diameter of a single layer of aggregates. Under these assumptions the dA value should express the diameter of the aggregates. It cannot be expected that the mechanisms of detainment will occur in accordance with these assumptions. Therefore, dA is defined as the magnitude characterising the dimension of aggregates forming the layer. The larger the aggregate dimensions the greater is dA and vice versa.
The Equation 3(b) is valid for s < scrit and for s ≥ scrit, ξ = ξmax. It expresses the changes in ξ from ξ = 1 to the value of ξmax which occurs when the media grain is covered by a layer of aggregates. Since the dimension of aggregates is several orders smaller than that of the media grain and assuming that aggregates are spherical then the ξmax can be established as the ratio of the surface area of the formed hemisphere to its projection, i.e. ξmax = 2. This would apply when based on the assumption that the affinity of the system aggregate-grain is the same as that of the system aggregate-aggregate. For the spherical aggregates it should apply that when ξmax < 2 the affinity of the aggregate-aggregate is smaller than the affinity of the aggregate-grain and it is vice versa for ξmax = 2.
When s > scrit, ξ = ξmax = constant, the product k1 ξ becomes the only constant in the range of s > scrit. The coefficient k1 is associated with adhesion forces. Because of this and because the surface of grains covered with the intercepted aggregates the most profound influence occurs at the beginning of the cycle when the function f(t) = 0 for s = 0 and then it starts increasing very slowly at first and its rate gradually increases. This occurs under the twin actions of adhesive forces and increasing coverage of grains. From this it can be presumed that when the value of the coefficient k1 increases the affinity of the system aggregate-grain improves. Taking the above into consideration it can be concluded that with increasing value of the coefficient k1 the affinity of the system aggregate-aggregate is also improving. Coefficient k1 expresses the common properties of media grain and flocculent aggregates. In this case, the properties of a grain refers to its surface activity only.
The f(t) increases starting from the zero to its maximum which occurs when the media capability to retain aggregates (l = 0) is exhausted. Therefore, the influence of coefficient k2 is manifested only at the time when the media layer is already covered by retained aggregates. From the above it can be concluded that when the coefficient k2 increases the affinity of the aggregate-aggregate system deteriorates. Consequently, the aggregates are less readily retained on one another and penetrate deeper into the bed. This coefficient is independent of the properties of media grains.
3. Test of Filterability
The effectiveness of deep-bed filtration with respect to suspension formed during the preceding processes is evaluated by the test of filterability [2] [4] [5] . The properties and concentration of the suspension entering the filter are affected by the efficiency of the preceding aggregation and separation processes. They are affected by the changes in the conditions of suspension formation, transport of suspension between the unit operations as well as by external influences. Therefore, the test of filterability becomes an indispensable tool for evaluating all the influences that may affect the filtration properties of a suspension.
Optimization of the properties of suspension with respect to filterability during its formation is of exceptional significance for the efficiency of filtration. Due to the influence of a broad spectrum of factors, filterability cannot be determined directly by a simple test. Nor can it be defined by a single parameter characterizing the properties of suspension such as, for example, sedimentation velocity for settleability of suspension.
The filterability of suspension should be determined preferably in a filtration pilot plant installed in the larger capacity waterworks. The pilot filtration plant permits various process arrangements which are not possible to verify in waterworks operation. When the installation of a pilot filtration plant is not possible and there is a need to establish filterability of suspension entering the filtration plant then filterability of such suspension should be determined by using the filtration element of a thin layer of filter media.
3.1. Filtration Pilot Plant
The filtration pilot plant consists of facilities for dosing of chemicals, flash mixer(s) for dispersion of dosed agent(s), flocculation plant with adjustable intensity of agitation and retention time and filtration plant (Figure 1). The filtration plant should be made of transparent PVC pipe of a diameter preferably greater than 200 mm. It should have the full height of the filter bed plus adequate pressure head corresponding at least to the filter bed height. A provision is needed for taking pressure readings and water samples in elementary distances say every 50 to max 100 mm throughout filter bed height. The cost of this pilot plant is negligible in comparison to that of the works and in any case it will be very quickly offset by benefits it provides for the works operation.
3.2. Filtration Element
The method of determining filterability, the design of the filtration element and the processing of the results obtained are based on the mechanistic model of filtration [1] - [4] [15] .
The properties of the suspension which is to be intercepted by deep-bed filtration cannot be determined with respect to any media other than a layer of a granular material. Therefore, the test of filterability is carried out in a filtration element with a thin layer of granular media. The filtration element must be charged with media having precisely defined properties of granularity, porosity and height. The filter element must also be equipped with facilities for measuring head-loss and flow rate. It must also be provided with water sampling points. These fa-
![]()
Figure 1. Filtration pilot plant arrangement. A—Flocculation chamber; B—single medium filtration column; C—dual media filtration column; B1—silica sand; C1—Hydro-anthrasit; C2—silica sand; 1—raw water inlet; 2—valve; 3—T-piece; 4—valve, 5—connecting pipe; 6—stirrer; 7—stirrer drive; 8—inlet connection to filtration column; 9—drain overflow; 10— false floor; 11—side taps; 12—tube type pressure gauge; 13—filtrate discharge; 14—gear pump; 15—coagulant dosing tank; 16—dosing pump.
cilities should not influence or interfere with the course of the filtration process. Furthermore, the filter element must be of such dimensions that it can be easily installed in all key places in the plant for direct determination of the filterability of the suspension formed upstream of such points. A filtration element of a suitable design with an elementary layer of granular media should satisfy all of these requirements.
The filtration element shown in Figure 2 is constructed out of perspex tubing of ID = 124 mm and is provided with fittings for connections to a pump and a differential pressure gauge. Usually it is charged with sand of grains carefully sieved to a size d = 1.00 - 1.20 mm to a height of 50 mm [2] . Water is pumped out from the filtration element with a positive displacement pump and flowrate is measured by a rotameter.
The installation arrangement of the filtration element is shown in Figure 3. The pressure indicator is mounted on a supporting structure. The flow through the filtration element is controlled by means of a gear pump fitted to a variable speed drive to ensure that the required constant rate of flow is maintained during the entire testing time. Flowrate is measured by a rotameter. The top of the media in the filtration element is accurately levelled.
![]()
Figure 2. Arrangement of a thin layer filtration element.
![]()
Figure 3. Plant arrangement for determination of filterability of suspension. 1—filtration element; 2—rotameter; 3—gear pump; 4—loss of head gauge.
Preparation of the filtration element for testing requires special attention. Filter sand of a mono-grain size must be used and the mass of the sand for the selected porosity must be calculated. The element should be provided with a circular gauge line 50 mm above the bottom plate to which sand is tapped down to produce the required porosity of the layer.
The filtration element should be installed at strategic places of the works where the filterability of suspension can be affected and is of importance. Usually it is placed at the outlet of the first separation stage or in the inlet flume to open rapid gravity filters, with the aim of evaluating the filterability of suspension leaving the first separation stage and entering the filters. The filterability of the suspension should also be determined at the end of the rapid and slow agitation units operation for comparison purposes. The direct influence of intensity of agitation and changes in the properties of suspension are evident from the shape of the curves indicating concentration of the selected determinant(s) in the filtrate plotted against head-loss measured across the filtration element.
The filtration element is submerged below the water level to ensure that the characteristics of the suspension to be filtered are representative. The following parameters are monitored at time intervals according to a preselected time schedule, namely, content of cation (Me) of the destabilisation agent used, rate of flow and loss of head and at the inlet and the outlet of the element.
From the filterability point of view the most important parameters are [2] :
Ø dimension of aggregates,
Ø magnitude of adhesion forces mutually binding the destabilised particles in the aggregates formed,
Ø magnitude of attraction force acting outside of the aggregates,
Ø character and magnitude of changes in the structure of aggregates which occur when it is subjected to the influence of shear stress.
The basic data for the calculation of a filtration cycle are obtained from the testing cycle with water containing the suspension the filterability of which is to be determined. The input data are obtained from filtration on a filtration element. The height of the filtration layer is the lowest possible and is so designed that pressure losses at the beginning of the filtration cycle are measurable with high accuracy. The layer height depends on grain size of the media and is designed to produce a pressure loss in the range between 5 and 10 mm at the flow of pure water through the layer. The pressure head above the filter layer which is required to overcome the resistance of the layer generated during filtration must be adequate to prevent development of sub-atmospheric pressure in the filter layer.
4. Computer Programme
The following initial data are the inputs to the computer model:
Ø Diameter of grains of a mono-grain filtration layer,
Ø Shape coefficient of grains,
Ø Height of layer,
Ø Porosity of clean layer,
Ø Area of filtration element,
Ø Kinetic viscosity of flowing water.
Further computer data are the group of values of the following five parameters monitored in each selected time interval:
Ø Time from the beginning of filtration,
Ø Concentration of the cation of destabilisation agent at the inlet into the element,
Ø Concentration of the cation of destabilisation agent at the outlet from the element,
Ø Head loss,
Ø Flowrate through the element.
The outputs of the computer model processing the above data are the values of k1, k2, xmax, dA, α, β, ψ and relative standard deviation for the assessment of accuracy of balanced values.
The mathematical formulations for the computer programme for the calculations of filterability of suspension are based on Equations (1) to (12). The method for determining filterability by means of filtration through a thin layer of granular media is based on comparing the performance data throughout the filtration cycles taking place under a maximum of identical conditions and a minimum of variables and ideally one variable only. This can only be achieved when testing is carried out in parallel to waterworks operation because under normal operation of the waterworks many operationally insignificant changes take place that can profoundly affect the results of the filterability tests.
5. Mechanistic Model of Filtration in Engineering Practice
Dependence of the coefficient of filtration efficiency and the specific volume of intercepted suspensions on a property of suspension formed with hydrolysing destabilisation agent at different localities, media grain size and filtration velocity is shown in Figures 4-6 [1] . Figure 7 [16] compares the head loss curves generated by two entirely different kinds of suspension, namely one produced by a mineral destabilisation agent and another one by a polymeric coagulant.
Figure 4 shows inter-dependence of the efficiency of filtration and the volume of intercepted suspension determined for the same filtration velocity (v = 5 m/h), the same grain size (d = 1 mm) and its shape coefficient (s = 0.885) on different properties of suspension. These curves indicate what grain size would be the most suitable for various water qualities. The larger the area covered by a curve the coarser the grain size should be. The reason is that the suspensions covering large areas are intercepted too easily and when grains of a small size are used the head loss would be generated too fast thus preventing the bottom layers of the bed from actively participating in filtration.
The effect of different grain sizes on the efficiency of filtration when the same suspension at the same filtration velocity is filtered is shown in Figure 5. As can be seen, the filtration efficiency of larger grains is smaller than that of smaller grains. Therefore, for two filters of different grain size to have the same filtration efficiency the one with a coarser grain must have a deeper bed.
![]()
Figure 4. Influence of water quality on filtration efficiency.
![]()
Figure 5. Influence of grain size on filtration efficiency.
![]()
Figure 6. Influence of filtration velocity on filtration efficiency.
![]()
Figure 7. Clogging of filter bed with different kinds of suspension-Michau pressure diagram.
The effect of different filtration velocities on the efficiency of filtration when the same water through the same filter bed is filtered is shown in Figure 6. As can be seen, higher filtration efficiency is achieved and more suspension is intercepted at a lower filtration velocity.
The effect of clogging of the filter bed when different kinds of suspension through the same filter bed at the same filtration velocity are filtered, is shown in Figure 7. Curve 1 shows deep penetration of suspension formed by the hydrolysing destabilisation agent (ferric chloride) into the filter bed utilising even its lowest layers of filter bed for filtration. Furthermore, the filter is operated under the positive pressure conditions in filter bed throughout the filtration cycle. The filtration cycle was 65.5 hours long. In contrast, Curve 2 shows that the suspension formed by polymeric coagulant builds-up head loss very rapidly and utilises only the upper-most layers of filter bed. Practically this means that deep-bed filtration is changed to surface straining. Furthermore, the filter has operated under the sub-atmospheric conditions in the filter bed for a great part of the filtration cycle as is evident from this curve. This is a very undesirable condition of operation. The filtration cycle was only 39 hours long.
6. Conclusions
1) The equations in the mathematical model of the mechanistic conception of filtration are derived from the basic theory of filtration. This enables the influence of water quality to be distinguished from other influences.
2) The mechanistic conception of filtration is based on the assumption that the instantaneous value of the coefficient of filtration efficiency λ is dependent on the magnitude of the resultant of adhesion and hydrodynamic forces acting in the filter bed. The adhesion forces enable interception of suspension on the surface of media grains or to the surface of already retained suspension. These forces are proportional to the surface of grains covered with intercepted suspension. The hydrodynamic forces prevent interception of suspension and are proportional to the shear stress.
3) The filtration cycle of the mechanistic model of filtration can only be calculated using a computer programme.
4) The properties of suspension which are best suited for separation by sedimentation or dissolved air flotation may not be best suited for separation by deep-bed filtration. The suitability of suspension produced by the preceding purification processes for deep-bed filtration is determined by the test of filterability. The test of filterability is an indispensable tool for evaluating the filtration properties of a suspension.
5) The proposed test of filterability is based on the mechanistic model of filtration. It is designed to assess the effect of variations in the chemical-physical conditions under which flocculent suspension is formed on filtration efficiency. The results obtained from the test of filterability also provide data for the optimization of such conditions in order to improve the overall efficiency of filtration. In addition, the test of filterability is designed to inform how various chemical agents affect filtration efficiency and performance of the filtration plant with respect to the length of the filtration cycle and the rate of increase in head loss. The test of filterability is also suitable for determination of the effects of external influences on the filterability of the suspension.
6) The inter-dependence of the coefficient of filtration efficiency and the specific volume of intercepted suspen- sion on
Ø The properties of different suspensions formed from waters of different quality with a hydrolysing destabilisation agent at different localities show that under the same operating conditions (filtration velocity, media grain size and water temperature) different filtration efficiency and different specific volume of intercepted suspension are obtained. In the evaluation diagrams the larger area covered by the filtration efficiency curves indicates a coarser media is more suitable.
Ø The media grain size shows that the coefficient of filtration efficiency of larger grains is lower than that of smaller grains. Therefore, to obtain the same filtration efficiency filter with a coarser media requires a deeper bed.
Ø The filtration velocity shows that a lower filtration velocity results in a higher coefficient of filtration efficiency and a higher specific volume of intercepted suspension than a higher filtration velocity.
7) The comparison of the effect of different kinds of suspensions on the generated head loss and the length of the filtration cycle shows that:
Ø A suspension formed by a mineral destabilisation agent penetrates deep into the filter bed utilising even its lowest layers for filtration. When adequate height of water above the filter bed is provided then the filter operates under positive pressure conditions throughout the filtration cycle.
Ø In contrast, a suspension formed by a polymeric coagulant builds up a head loss very rapidly and utilises only the upper-most layers for filtration. As a result, then the filter even when an adequate height of water above the filter bed is provided, operates under sub-atmospheric conditions for the greater part of the filtration cycle.
Ø The length of the filtration cycle attained with ferric chloride formed suspension was 65.5 hours whereas with polymeric coagulant formed suspension it was only 39.0 hours.
8) The mathematical model of the mechanistic conception of filtration permits the calculation of the course of the filtration cycle for various design parameters of a filter for a specific suspension.
NOTES
*Corresponding author.