1. Introduction
In the previous paper [1] , we laid the groundwork for what was referred to as Computational Intelligence (CI). In this paper we will further this discussion and offer some new insights. We discussed how intelligence could be thought of as an entropy minimizing process. This entropy minimization process, however comes at a cost.
Recall from [1] [2] that whenever a system is taken from a state of higher entropy to a state of lower entropy, there is always some amount of energy involved in this transition, and an increase in the entropy of the rest of the environment greater than or equal to that of the entropy loss [2] . The negative change in entropy will require some amounts of work,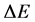 .
.
The central concept of this paper concerns how smaller concepts aggregate together into larger and more complex structures. This process is a function of the complexity of each element, and the energy available to the system. The complexity of the components will delegate the degrees of freedom available to associate with parts of other constituents. The amount of energy available must be enough to supply the constituents with energy necessary to fulfill this task. We call this association between participating degrees of freedom a bond, and assert that the degrees of freedom that form the bond are covariant and thus have minimal entropy than that of the other degrees of freedom, respectively.
Though we will primarily be concerning ourselves with numerical data, it should be stressed that these concepts are applied to a panoply of possibilities including everything from subatomic particles, to atoms, to social groups, to politics. Here, the concept of energy is taken in the computational sense. That is, computational energy refers to the amount of computational work required to form bonds.
2. Creating Structure
In virtually all facets of nature, more complicated structures are formed by less complicated structures, after the addition of some amount of energy. Suppose the set 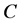 contains
contains 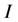 constituents, each with a certain quantity of degrees of freedom J as expressed in notation:
constituents, each with a certain quantity of degrees of freedom J as expressed in notation: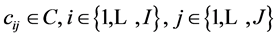 . For example, a carbon atom has four valence electrons available for use in forming bonds. Note that the
. For example, a carbon atom has four valence electrons available for use in forming bonds. Note that the 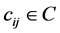 need not be homogeneous, as (continuing with our example from Chemistry) a carbon atom is free to form bonds with other elements and molecules. We shall call the aggregation of these constituents a meme, a term coined by Richard Dawkins in the Selfish Gene [3] .
need not be homogeneous, as (continuing with our example from Chemistry) a carbon atom is free to form bonds with other elements and molecules. We shall call the aggregation of these constituents a meme, a term coined by Richard Dawkins in the Selfish Gene [3] .
Let us further suppose that with each of these degrees of freedom, 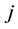 , there is a certain amount of energy required to participate in the formation of a more complicated structure, and all degrees of freedom participate. This relationship may not be linear. Let
, there is a certain amount of energy required to participate in the formation of a more complicated structure, and all degrees of freedom participate. This relationship may not be linear. Let 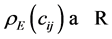 denote the energy for each respective
denote the energy for each respective . Then the total energy,
. Then the total energy,  , required to form a more complex structure, or activation energy, from
, required to form a more complex structure, or activation energy, from  is therefore
is therefore
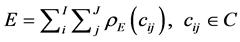 . (1)
. (1)
Again, it is worth noting that although the term “energy” derives from physics, we can take it in this particular context to have a more general meaning, in terms of the computational effort required to establish the bond between degrees of freedom.
Applications to Data Mining
We can begin to draw immediate relevance to data mining. To make sense of a data set, we must determine the elements that are correlated and thus have minimal entropy with respect to the others. Some of these degrees of freedom will participate; others will not bear any relevance. Further, some elements may not contain any information at all, as is the case with sparse data sets.
It is an active area of research to sieve out data with more information content for use in classification or clustering. Processes such as PCA or Cholesky transformation are used to reduce the amount of feature vectors for classification and find a transformation to a basis. This has a clearly defined interpretation in Linear Algebra, though we argue that information content may be another potential approach.
It is not uncommon to deal with data sets where each element is characterized by thousands or hundreds of thousands or feature vectors or more [4] . Computationally intensive techniques like PCA or the Cholesky transformation may prove intractable for data sets of this magnitude.
Under our framework here, using entropic self-organization [1] the entropy contribution of redundant data would be very small, and that of random datavery large. In such a context, meaningful data would be seen as a comparable deviation between these two extremes.
All the notions of this section assume, of course, that the data has been properly preprocessed. After all, treating all data in an unfiltered topological sense would fail for such data sets as the iris data set, and in natural language processing.
3. Meme Amplitude
Now that we have determined the total energy necessary for a meme to reach the next state, let’s talk about the transition from one state to another. In this case let , or the difference between the activation energy and the resting energy, or the energy required to sustain the elements unadulterated. Using
, or the difference between the activation energy and the resting energy, or the energy required to sustain the elements unadulterated. Using , we can speak of the relative energy,
, we can speak of the relative energy, 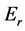 or the initial energy less
or the initial energy less . Let us further suppose that this
. Let us further suppose that this 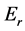 can be described at some time
can be described at some time ![]() by some function,
by some function, ![]() that we may also refer to as the meme amplitude.
that we may also refer to as the meme amplitude.
Let us take into account some considerations for![]() . The rate of change in
. The rate of change in ![]() is almost certainly proportional to
is almost certainly proportional to ![]() itself, as the rate of change in the energy of the system should be proportional to that which it already has. If we include a constant of proportionality which we will call affinity
itself, as the rate of change in the energy of the system should be proportional to that which it already has. If we include a constant of proportionality which we will call affinity ![]() then we have the familiar
then we have the familiar![]() , but taking into account the fact that
, but taking into account the fact that ![]() is a boundary for
is a boundary for![]() , we have the familiar logistic equation
, we have the familiar logistic equation
![]() (2)
(2)
onto which we impose the following boundary conditions
1) At![]() ,we start at our initial state,
,we start at our initial state, ![]()
2) As![]() .
.
The latter implies that after some time, the transition to ![]() should be final, or that
should be final, or that ![]() should come arbitrarily close to
should come arbitrarily close to ![]() as time progresses.
as time progresses.
3.1. Solutions
Equation (2) has been well studied, and its solutions fall into a broad class of functions known as sigmoid functions known for their characteristic “S” shape [5] , and who’s applications range from their use as cumulative distribution functions in probability and statistics to activation functions in artificial neural networks. Due to the first boundary condition, we restrict the solution to![]() , which cuts off the left hand side of this “S” shape, or translates the entire curve such that the lower asymptote is suitably close to
, which cuts off the left hand side of this “S” shape, or translates the entire curve such that the lower asymptote is suitably close to![]() .
.
3.1.1. Growth Rate
Some comments should be made on the growth rate A. This constant will determine the rate of change in the sigmoid curve. With increasing A, the curve gets steeper and the time to reach the meme amplitude decreases. We will use the term aggressive to refer to large A. For drastically large A, the sigmoid curve approaches a step function. A will also depend on the energy applied to the system, ![]() , and will itself have its own boundary conditions, as the dynamics described by 2 will often break down for
, and will itself have its own boundary conditions, as the dynamics described by 2 will often break down for![]() »
»![]() . For example Carbon forms graphite at (relatively) low energies, but for higher energies, it forms diamonds. This is a function of the amount of valence electrons used in the bonding process (3 and 4 for graphite and diamond, respectively). A similar analogy may be made for data and the computational effort we are willing to put into the entropic self-organization algorithm.
. For example Carbon forms graphite at (relatively) low energies, but for higher energies, it forms diamonds. This is a function of the amount of valence electrons used in the bonding process (3 and 4 for graphite and diamond, respectively). A similar analogy may be made for data and the computational effort we are willing to put into the entropic self-organization algorithm.
3.1.2. Amplitude
The meme amplitude is certainly not restricted to a single meme amplitude, at least not in the general case. Once the transition ![]() has been, we are free to apply the logic successively to determine the next successive meme amplitude and so forth. We will call the repeated demonstration of meme amplitude growth via 2 the hierarchical aggregation paradigm.
has been, we are free to apply the logic successively to determine the next successive meme amplitude and so forth. We will call the repeated demonstration of meme amplitude growth via 2 the hierarchical aggregation paradigm.
3.1.3. Extrema
Although the solutions to 2 are monotonically increasing, some subtle nuances in its curvature provide useful insights. Consider the second derivative, which is may be easily obtained from Equation (2),
![]() . (3)
. (3)
The second rate of change happens at the roots of this equation, which are![]() . The first and last
. The first and last
are clearly the asymptotes, when the energy levels off. It is the middle root that is of interest. After all, if sus-
tainable growth is to occur, there must be a transition in the sign of the growth rate. This happens at![]() .
.
3.2. Stability and Sustainability
The reality of the dynamics described by 2 is not always so clement and predicable in reality. Although often the affinity may be treated as constant to make calculations and estimations easier, in reality it may be a function of the applied energy, and valid in some kind of threshold. If the applied energy level is outside of this threshold, the model will break down.
Further, once the affinity has been determined it can be used as an indicator of the stability that the transition to the next energy level will occur. By observing the disparities between the model 2, and observed data, we can gain an idea as to if this transition will occur, or if the model will return to its previous energy state, or even one below.
If we remove the bounded-ness condition, Equation (2) simply becomes
![]() , (4)
, (4)
whose solutions are exponential for positive A. However unbounded growth is unsustainable and leads to unpredictable behavior. If we observe the behavior described in 4 as opposed to 2, we may have an indicator of collapse. Additionally, if the rate of growth is not commensurate with the particular value of A, the stability of the energy level transition may be suspect.
Once the transition to the next energy level has been made, there is a certain amount of energy necessary to sustain it. If this energy gets outside of the threshold, the model will not be able to maintain this energy level. Thus the new energy level is not guaranteed to indefinitely stable.
The calculation of A, its threshold, and energy to sustain it is always contingent upon underlying factors unique to the system. These must be taken into account, which may not be tractable, but perhaps at least estimable.
3.3. Bubbles
Our discussion in Section 3.2 has many applications and is of great importance especially to society as of the past five years. We can draw examples in real estate, financial markets, and population growth. Indeed this mathematics may be used to identify sustainable growth, or bubbles, periods of extraordinary inflationary growth followed by abject collapse.
For example, consider the well-studied behavior exhibited in the growth of bacterial colonies. There is an initial lag phase as the RNA of the bacteria start to copy, followed by an explosion of exponential growth called the growth phase, followed by a brief period of stability before the bacteria exhaust their resources resulting in an expedient decay.
3.3.1. Determining Bubbles
It may be difficult to determine whether a given data set is a bubble in the making or the initial stages of a stable transition, though we may gain insight by the application of two observations discussed in this paper.
First, if we are able to calculate the affinity constant, and activation energy, and we notice a disparity in the dynamics the system is exhibiting and that which was forecasted using these constants, then we may have reason to believe a bubble may be forming. Bubbles are caused by disproportionately excessive growth or extraneous factors distorting the dynamics of the system. But such factors are not perpetual and eventually the true dynamics of the system will take over. At this point, the system will fall to its natural energy state, commensurate with our calculations and what the system is able to support.
Second, consider the rate of change. After all, we may not be privy to the subtle inner workings of the system so as to calculate the necessary parameters. This may be especially true in very large and complicated systems, where subtle factors may contribute greatly to the outcome of the calculation. We can fall back on our discussions in Section 3.1.3. After all, if the system is exhibiting extraordinary growth, in order to fit model 2, there must be a point at which rate of change of the growth rate reaches zero as given in Section 3. We may not be able to determine this a priori, but we might be able to hypothesize whether the activation energy inferred from a given point is fungible or not.
3.3.2. Remarks
The difficulty of calculating the activation energy of large and complicated systems should be stressed. After all, there may be a panoply of factors that will influence the overall dynamics of the model, and they can be highly nonlinear.
4. Outliers
In the previous section, we considered the amplitude of only single meme. Now we will consider meme amplitude in the presence of other memes. In order to repeat the logic of Section 3, we must introduce the interaction matrix![]() , which represents the effect meme i has on meme j. The underlying mechanics behind these
, which represents the effect meme i has on meme j. The underlying mechanics behind these![]() ’s include resource allocation, and direct competition. Thus, in the presence of
’s include resource allocation, and direct competition. Thus, in the presence of ![]() memes, Equation (2) becomes
memes, Equation (2) becomes
![]() (5)
(5)
where the constant ![]() can be absorbed into the interaction matrix,
can be absorbed into the interaction matrix, ![]() withouta functional effect on the resulting solutions [6] . Therefore Equation (5) becomes
withouta functional effect on the resulting solutions [6] . Therefore Equation (5) becomes
![]() (6)
(6)
This is recognized as a Lotka-Volterra equation commonly referred to as the competition equation. This is another very well studied class of differential equations for which results can be found in [6] - [12] just to name a few.
5. Conclusions
In this paper, we discussed some ramifications of the original principal detailed in [1] . In essence, the subject of this paper could be summarized as how data aggregates together to form more complex memes, how this is effected by the presence of multiple memes, and the conditions under which this transition may or may not be stable. We also looked at some practical examples of these principals in source code.
There is still a great deal of room for future improvements. First, we can improve our understanding of the affinity parameter A and how to better calculate it. We can also apply this knowledge to more areas of study so as to be able to effectively calculate predictable amplitude transitions, burgeoning growth or bubbles.
Additionally, we also wish to study the most basal layers of meme aggregation and creation including the fundamental constituents, how they emerge to form systems, and how these systems can aggregate hierarchically as meme amplitude growth describes. We will also look at how this process is perpetuated in computational processes, as opposed to information in static elements and datasets.