1. Introduction
Refrigeration and air conditioning consume an enormous amount of energy. Solar-powered plants allow the saving of an important amount of energy compared to electric driven ones. Heat driven absorption refrigeration has get more and more attention. Unlike vapor compression refrigerator, absorption refrigerator could be driven by various energy sources. The system uses thermal energy to produce cooling, and thus waste heat and other forms of low grade heat can be employed, especially solar energy. Absolute low noise is also one of their prevailed advantages. Moreover, they cause zero or minimum ozone depletion because they do not use any CFC or HFCs refrigerant as working fluid [1] . From these points of view, the solar-assisted absorption refrigeration shows a very promising future. Usually, the maximum demand for cooling coincides with the maximum availability of solar radiation, whereas conventional electric driven systems have the problem of providing their minimum capacity in the hottest day hours [2] . In addition, the use of solar energy in refrigeration can be very useful to limit the growth of the electric energy demand in summer and for sustaining the development of technologies based on renewable sources of energy. Several authors presented studies of solar refrigeration systems in [3] - [6] .
In the theory of classical thermodynamics, the cyclical model of an absorption refrigerator is treated in [7] as reversible four-heat-sources cycle, which consists of four reversible adiabatic and four reversible isothermal processes. In order to achieve the coefficient of performance (COP) of reversible four-heat-source refrigeration cycles, the isothermal parts of the cycle have to be carried out infinitely slow because of the presence of the thermal resistances. The cooling rate of the resulting refrigerates or trends to zero because an infinite time is taken to draw a finite amount of heat from the cooled space. Real absorption refrigerators are designed to deliver a certain amount of cooling load. It is usually too rough to predict the coefficient of performance of real absorption refrigerators so that it is necessary to develop a new theory for absorption refrigeration cycles. Finite time thermodynamics (FTT) has emerged during the last three decades as a distinct subfield in heat transfer [8] . The method consists of the simultaneous application of heat transfer and thermodynamic principles in the pursuit of realistic models of heat transfer processes, devices, and installations, i.e., models that account for the inherent irreversibility of heat, mass, and fluid flow processes. The original objective of the finite time thermodynamics appears to reduce the differences between the predictions of classical thermodynamics and the results of real practice. The results obtained for varying thermodynamic cycle analyses by using FTT are closer to real device performance than those using classical thermodynamics [9] . In literature, several researches have been focusing on the performance optimization of refrigerators, based on endoreversible models in [10] - [12] and on irreversible models in [13] [14] .
Steady-state models are useful under several conditions, although under strongly dynamic conditions that are often seen in real-life operation, these models are unacceptably and inaccurate [15] . However, steady state models do not provide time dependent information on the thermal behavior of absorption refrigerators and are therefore not suitable for transient system simulations. In order to predict the performance of these chillers under all aspects of operation, dynamic simulations must be developed. Vargas et al. in [16] conducted a simulation of a solar collector driven water heating and absorption cooling plant using the three-heat-reservoir cycles via multi objective optimization. They concluded that the minimum pull-down and pull-up times, and maximum of the second law efficiencies found with respect to the optimized operating parameters are important. Recently, Hamed et al. in [17] presented a thermodynamic transient regime simulation of a solar driven absorption refrigerator. An endoreversible model has been analyzed numerically to find the optimal conditions of a solar driven absorption refrigerator. Based on the latest reference, the main focus of this study is concentrated on the simulation of the transient behavior of the endoreversible model of a three heat reservoirs absorption heat transformer, with Newton’s heat transfer law with a detailed solar energy process. For a practical set of cold source temperatures 8˚C, 0˚C and −8˚C, the purpose of this paper is to investigate the effect of solar collector stagnation temperature and cold temperature on time set point temperature, entropy generated inside the cycle and finally evaporator heat.
Solar collectors are broadly classified as, non-concentrating and concentrating type collectors. Flat-plate collectors are the most widely used kind of collectors in the world [18] . In this analysis, the collector adopted is a flat-plate collector. Flat-plate solar collectors are commonly used in solar space heating. It is economically adopted when the same collector is used for both heating and cooling spaces. However, regarding the relatively low temperatures attainable, only a few practical applications are available in flat-plate solar operated cooling processes.
2. Mathematical Model
The solar driven absorption refrigeration cycle and its equivalent model are shown in Figure 1(a) and Figure 1(b). The cycle is considered to be endoreversible, i.e. internally reversible and externally irreversible. Internal irreversibilities are assumed negligible in presence of the heat exchange irreversibilities due to finite temperature differences. Internal irreversibilities due to heat transfer, throttling, mixing and internal dissipation of the working fluid, which are responsible for the entropy generation are always present in a real heat driven refrigerator [4] .
Also, it is assumed that there is no heat loss between the solar collector and the generator and no work exchange occurs between the refrigerator and its environment. The work input required by the solution pump is negligible regarding the energy input to the generator.
The heat transfers between the working fluid in the heat exchangers and the external heat reservoirs are car-
![]() (a) (b)
(a) (b)
Figure 1. (a) Schematic of a solar driven adsorption refrigeration system; (b) Equivalent endoreversible model.
ried out under a finite temperature difference and obey the linear heat-transfer law “Newton’s heat transfer law’’. Therefore, the steady-state heat transfer equations for the three heat exchangers can be expressed as:
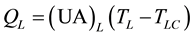 (1)
(1)
 (2)
(2)
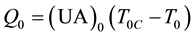 (3)
(3)
From the first law of thermodynamic:
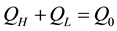 (4)
(4)
According to the second law of thermodynamic and the endoreversible property of the cycle, we have:
 (5)
(5)
The generator heat input 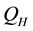 could be estimated by the following expression:
could be estimated by the following expression:
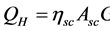 (6)
(6)
where 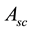 represents the collector area,
represents the collector area,  is the irradiance at the collector surface and
is the irradiance at the collector surface and  stands for the collector efficiency. The efficiency of a flat plate collector can be calculated, according to [3] and [5] as:
stands for the collector efficiency. The efficiency of a flat plate collector can be calculated, according to [3] and [5] as:
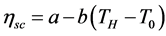 (7)
(7)
where 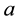 and
and 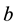 are two constants.
are two constants.
Equation (7) can be rewritten by introducing the collector stagnation temperature 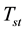 as follows:
as follows:
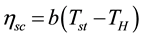 (8)
(8)
where ![]() (for which
(for which![]() ) is given by:
) is given by:
![]() (9)
(9)
The equation for heat input ![]() can be rewritten by combining Equations (6) and (8) as follows:
can be rewritten by combining Equations (6) and (8) as follows:
![]() (10)
(10)
The thermal inertia of the refrigerated space is large enough such that the transient operation of the refrigerator can be neglected when compared to the time evolution of the temperature inside the refrigerated space. The transient regime of cooling is accounted for by writing the first law of thermodynamics, as follows:
![]() (11)
(11)
where ![]() is the rate of heat gain from the walls of the refrigerated space and
is the rate of heat gain from the walls of the refrigerated space and ![]() is the load of heat generated inside the refrigerated space.
is the load of heat generated inside the refrigerated space.
The factors![]() ,
,![]() and
and ![]() represent the overall thermal conductances of the heat exchangers. The overall thermal conductance of the walls of the refrigerated space is given by
represent the overall thermal conductances of the heat exchangers. The overall thermal conductance of the walls of the refrigerated space is given by![]() . Since
. Since![]() ,
,![]() and
and ![]() are not known, the following constraint is introduced at this stage:
are not known, the following constraint is introduced at this stage:
![]() (12)
(12)
According to the cycle model mentioned above, the rate of entropy generated by the cycle is described quantitatively by the second law as:
![]() (13)
(13)
To provide the model more general, a dimensionless form of the set of equations is preferred, using different reference parameters (as described below). Therefore, it is convenient to search for an alternative formulation that eliminates the physical dimensions of the problem. In a dimensionless model all variables are directly proportional to the dimensional ones presented in Equations (1) to (13).
The complete set of no dimensional equations for the model, including the absorption refrigerator steady state equations is:
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
where the following non-dimensional transformations are imposed:
![]() (22)
(22)
here, ![]() is the parameter which describes the size of the collector relative to the cumulative size of the heat exchangers, and
is the parameter which describes the size of the collector relative to the cumulative size of the heat exchangers, and![]() ,
, ![]() and
and ![]() are the conductance allocation ratios, defined by:
are the conductance allocation ratios, defined by:
![]() (23)
(23)
According to the constraint property of thermal conductance UA in Equation (12), the thermal conductance distribution ratio for the condenser can be written as,
![]() (24)
(24)
3. Simulation Results and Analysis
Using the models presented above, numerical simulations are conducted. The initial conditions are the heat generated inside the refrigerated space![]() , conductance allocation
, conductance allocation ![]() and the desired temperature in the refrigerated space. The system behavior is mainly determined by the driven hot temperature and cooling temperature.
and the desired temperature in the refrigerated space. The system behavior is mainly determined by the driven hot temperature and cooling temperature.
The principle main cooling applications are deep freezing (![]() to −20˚C), ice making (
to −20˚C), ice making (![]() to 0˚C) and chilling (
to 0˚C) and chilling (![]() to 15˚C). The refrigerated space temperature to be achieved take three values 8˚C, 0˚C and −8˚C, in dimensionless parameters they are
to 15˚C). The refrigerated space temperature to be achieved take three values 8˚C, 0˚C and −8˚C, in dimensionless parameters they are![]() ,
, ![]() and
and![]() . For these three cases, the numerical results are shown in Figure 2 to Figure 8. The validated system model can be used to predict system performance at different operating states. The results of computations based on this analysis are various and significant. They point out different operational regimes of the system, namely maximum power output or minimum dissipation (entropy generation) dependently on the studied case. Also, they show the limits of the variation range for the model variables, as well as reasons to choose the best solution between the physical ones.
. For these three cases, the numerical results are shown in Figure 2 to Figure 8. The validated system model can be used to predict system performance at different operating states. The results of computations based on this analysis are various and significant. They point out different operational regimes of the system, namely maximum power output or minimum dissipation (entropy generation) dependently on the studied case. Also, they show the limits of the variation range for the model variables, as well as reasons to choose the best solution between the physical ones.
Time is an important factor in the cooling system for particular cooling period. Hence, at constant heat source temperature ![]() and for different values of the collector stagnation temperature
and for different values of the collector stagnation temperature ![]() the variation of the time set point temperature with the collector size is calculated (Figure 2).
the variation of the time set point temperature with the collector size is calculated (Figure 2).
The time set point temperature decreases gradually according to the collector size parameter until reaching a minimum time then it increases in each case of imposed collector stagnation temperature and refrigerated space temperature. The existence of an optimum for the thermal energy input ![]() is not due to the endoreversible model aspects. However, an optimal thermal energy input
is not due to the endoreversible model aspects. However, an optimal thermal energy input ![]() results when the endoreversible equations are constrained by the recognized total external conductance inventory, UA in Equation (12), which is finite, and the generator operating temperature
results when the endoreversible equations are constrained by the recognized total external conductance inventory, UA in Equation (12), which is finite, and the generator operating temperature![]() . These constraints are the physical reasons for the existence of the optimum point. The minimum time to achieve prescribed temperature is the same for different values of the stagnation temperature
. These constraints are the physical reasons for the existence of the optimum point. The minimum time to achieve prescribed temperature is the same for different values of the stagnation temperature![]() . Then, for each imposed value of the stagnation temperature, the dimensionless collector size parameter has a specific variation range decreasing continuously as the collector stagnation temperature increases. For example, at
. Then, for each imposed value of the stagnation temperature, the dimensionless collector size parameter has a specific variation range decreasing continuously as the collector stagnation temperature increases. For example, at ![]() and
and![]() , B can vary between 0.337 and 1.126, while at
, B can vary between 0.337 and 1.126, while at![]() , it varies from 0.034 to 0.111.
, it varies from 0.034 to 0.111.
The results plotted in Figures 3-5 illustrate the minimum time ![]() to reach the desired set point temperature in the refrigerated space and the optimal parameter
to reach the desired set point temperature in the refrigerated space and the optimal parameter ![]() respectively against the stagnation temperature
respectively against the stagnation temperature![]() , thermal load inside the cold space
, thermal load inside the cold space ![]() and conductance fraction v.
and conductance fraction v.
It can be observed from Figure 3 that the minimum time to achieve the prescribed temperature is independent of the collector stagnation temperature. This is due to the heat absorbed by the generator that is quite constant regarding the stagnation temperature variation [17] . If the generator heat input is constant, the dimensionless collector size B in Equation (17) will decrease with higher collector stagnation temperature and the temperature of the generator Equation (15) is also constant. The time set point temperature decreases with the increase of the refrigerated space temperature. For instance, at cold source temperature ![]() equal to 0.943, 0.916 and 0.889 the set point temperature
equal to 0.943, 0.916 and 0.889 the set point temperature ![]() values are respectively 6.83, 7.85 and 9.45.
values are respectively 6.83, 7.85 and 9.45.
This is due to the fact that the temperature of the evaporator starts to decrease linearly then it decreases. Here, the reaction of the evaporator is strongly affected by the generator behavior. Its temperature starts rising linearly, then it becomes stable. As the temperature of the generator is higher more heat is absorbed in the evaporator. While, the temperature of the evaporator decreases slowly, the temperature of the generator is maintained quit constantly, indicating that the equilibrium state has reached. As a result, the optimal dimensionless collector size B decreases monotonically as ![]() increases. Also, one can see that the stagnation temperature
increases. Also, one can see that the stagnation temperature ![]() is limited, its value of 1.8 for the first case
is limited, its value of 1.8 for the first case![]() , 2.2 for the second case
, 2.2 for the second case ![]() and 3 for the third case
and 3 for the third case ![]() being impossible because of the above mentioned condition regarding the refrigerated space temperature
being impossible because of the above mentioned condition regarding the refrigerated space temperature ![]() desired which is not achieved.
desired which is not achieved.
From the curves of Figure 4, as the stagnation temperature ![]() and the heat source temperature
and the heat source temperature ![]() are constant, there is a clear proportionality between the minimum time set point temperature and the thermal load in the refrigerated space. The minimum time
are constant, there is a clear proportionality between the minimum time set point temperature and the thermal load in the refrigerated space. The minimum time ![]() increases respectively when the thermal load
increases respectively when the thermal load ![]() increases and the cold temperature
increases and the cold temperature ![]() decreases. This implies that the minimum time is strongly influenced by the thermal load and the cold temperature. As the load of heat generated inside the cold space is higher, less heat
decreases. This implies that the minimum time is strongly influenced by the thermal load and the cold temperature. As the load of heat generated inside the cold space is higher, less heat
is absorbed at the evaporator, causing a decrease of the temperature of the evaporator. Also the cold temperature decreases with time. Figure 4 reveals that the thermal load inside the cold space has an almost negligible effect on optimal dimensionless collector size, whereas a decrease in the ![]() leads to a decrease in
leads to a decrease in![]() .
.
Similar characteristics were obtained concerning the behaviors of the set point temperature and the optimal collector size according to conductance allocation ratios, as shown in Figure 5.
The total entropy generated inside the cycle function up to θset given in Equation (21) can be plotted with respect to the dimensionless collector size B for various stagnation temperature parameters Γst and cold temperature and at constant heat source temperature as shown in Figure 6.
A specific B value exists that minimizes the entropy function for given Γst and ΓL values. The curves show
clearly a reverse proportionality between the internal entropy generation and the stagnation temperature. Then, for each imposed value of the stagnation temperature, the dimensionless collector size has a specific variation range (imposed by the condition S > 0) continuously decreases as the efficiency increases.
The optimization with respect to the stagnation temperature is pursued in Figure 7 for minimum total entropy generated up to set point temperature and optimal dimensionless collector size. It is observed that ![]() is independent of Γst, whereas a decrease in the cold temperature leads to an increase in
is independent of Γst, whereas a decrease in the cold temperature leads to an increase in![]() . For instance, at a cold source temperature
. For instance, at a cold source temperature ![]() equal to 0.943, 0.916 and 0.889 the minimum total entropy generated values are respectively 0.018, 0.118 and 0.229. The cold temperature decreases with time. The total entropy inside the cycle
equal to 0.943, 0.916 and 0.889 the minimum total entropy generated values are respectively 0.018, 0.118 and 0.229. The cold temperature decreases with time. The total entropy inside the cycle
is strongly affected by the time. It rises with the increase of time. On the basis of the second law of thermodynamics, the entropy production is always positive for an externally irreversible cycle.
From Figure 7, when the stagnation temperature increases then the collector optimal size decreases. This result brings to light the need for delivering towards the greatest values of Γst to approach the real refrigerator. However, the stagnation temperature Γst is limited.
In this final section, the solar absorption refrigerator is considered to operate according to a closed cycle at steady state. Figure 8 reveals clearly the relationship between the evaporator heat with dimensionless collector size at constant heat source temperature and for three different values respectively of the collector stagnation temperature and the cold source temperature. It can be identified from the results that the cooling capacity increases from the startup of the refrigeration system. This phenomenon is typical of the system start-upworking
regime when there is a refrigerant hot flow inside the evaporator that would heat the interior while the refrigeration system cooling capacity increases. When the steady state conditions are attained in the refrigerator the evaporator heat transfer reaches a maximum. The maximum cooling capacity obtained for the tested refrigerator remains constant with the stagnation temperature. Then, for each imposed value of![]() , QL has a specific variation range continuously decreasing while B increases. The maximum evaporator heat transfer variation shown by the curves increases when the cold temperature decreases, as is demonstrated with the result for
, QL has a specific variation range continuously decreasing while B increases. The maximum evaporator heat transfer variation shown by the curves increases when the cold temperature decreases, as is demonstrated with the result for![]() ,
, ![]() ,
, ![]() ,
, ![]() and finally
and finally![]() ,
,![]() . It may be concluded that
. It may be concluded that ![]() is more affected by
is more affected by ![]() than by
than by![]() .
.
4. Conclusions
In this paper a dynamic model of a solar driven absorption refrigerator has been presented. An externally irreversible but internally reversible model has been employed to analyze the optimum conditions for which the maximum refrigeration effect can be achieved.
The cycle analysis has been studied under standard and variable working conditions. The results also supplied the initial conditions of the simulation of absorption performances. The existence of a collector optimal size for minimum time to reach a specified temperature in the refrigerated space, minimum entropy generation inside the cycle and maximum refrigeration rate was demonstrated. Appropriate dimensionless groups were identified and the generalized results reported in dimensionless charts.
The following conclusions could be derived:
・ The minimum time to reach the prescribed temperature in the refrigerated space depends strongly on the cold temperature and the thermal load on the cold space but remains constant with the stagnation temperature variation.
・ The minimum time set point temperature and collector optimal dimensionless size are influenced analogously by the thermal load in the refrigerated space and by the thermal conductance of the walls.
・ ![]() is independent of
is independent of![]() , whereas a decrease in
, whereas a decrease in ![]() leads to an increase in
leads to an increase in![]() .
.
・ The maximum evaporator heat transfer increases when the cold temperature decreases, but remains constant as the stagnation temperature increases.