Bohr’s Spectrum of Quantum States in the Atomic Hydrogen Deduced from the Uncertainty Principle for Energy and Time ()
1. Introduction
The Bohr model of the hydrogen atom [1] assumed circular trajectories for electrons circulating about the atomic nucleus and the motion along these trajectories has been quantized. In effect definite radii of the orbits
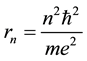 (1)
(1)
and electron velocities on these orbits
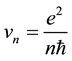 (2)
(2)
could be calculated. From the balance of the electron energy
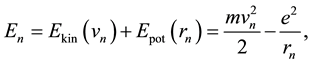 (3)
(3)
in which 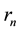 and
and 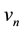 are substituted from (1) and (2), a well-known quantum formula
are substituted from (1) and (2), a well-known quantum formula
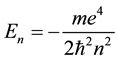 (4)
(4)
could be obtained. Later it became possible to derive the same 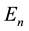 formula on the basis of a quantum- mechanical approach [2] .
formula on the basis of a quantum- mechanical approach [2] .
The classical Bohr model stimulated several questions concerning its validity, the main of which was perhaps how the electron―in course of its transition to another orbit―can choose that orbit and become limited in its further motion to it [3] [4] . In other words the problem was concerning not so much separate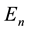 , but their differences
, but their differences
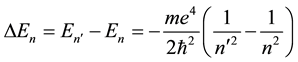 (5)
(5)
for some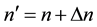 , and the way how (5) can define the atomic spectrum.
, and the way how (5) can define the atomic spectrum.
The present paper tends to meet this question in case when an approach to the energy spectrum is done on the basis of the uncertainty principle, the essence of which are the energy differences 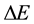 applied together with the time intervals
applied together with the time intervals
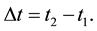 (6)
(6)
In fact the principle expressed in the form given by Heisenberg [5]
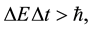 (7)
(7)
where  is a difference of energy met in the quantum process, and has been next objected on many occasions [6] - [8] . The effect of that numerous textbooks on physics or quantum mechanics do not even mention the validity; see e.g. [9] . Nevertheless a modification of (7) into a new formula
is a difference of energy met in the quantum process, and has been next objected on many occasions [6] - [8] . The effect of that numerous textbooks on physics or quantum mechanics do not even mention the validity; see e.g. [9] . Nevertheless a modification of (7) into a new formula
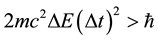 (8)
(8)
could be performed [10] - [12] and we show below that this transformation makes the uncertainty principle suitable in obtainig the atomic spectrum; the Formula (7) is fully ineffective at that point.
But before the spectrum is demonstrated, our aim is to point out that (8) can give also the lower bounds of the space intervals, say that along the Cartesian coordinate 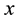 which is
which is
![]() (9)
(9)
This result can give a similar lower bound of the time intervals (6) met in the quantum processes.
2. Lower Bounds of the Position and Time Intervals Derived from the Uncertainty Principle for Energy and Time
Heisenberg [5] has coupled the observables which are the intervals of the position coordinate and that of momentum in the uncertainty relations similar to that given in (7) for the energy and time. Mathematically this is expressed by the formula
![]() (10)
(10)
on condition that only the ![]() -coordinates of the particle momentum and position are taken into account. Though the observables of a pair in (10) enter the formalism on an approximately equal footing, their experimental background can be much different. For example the momentum of a particle is usually much more accurately defined than its position. A similar property concerns the energy intervals which are easier accessible than those of time, but―contrary to (7)―the mutual position of
-coordinates of the particle momentum and position are taken into account. Though the observables of a pair in (10) enter the formalism on an approximately equal footing, their experimental background can be much different. For example the momentum of a particle is usually much more accurately defined than its position. A similar property concerns the energy intervals which are easier accessible than those of time, but―contrary to (7)―the mutual position of ![]() and
and ![]() in (8) is evidently different.
in (8) is evidently different.
The Relations (10) and (7) imply no limits for![]() ,
, ![]() , as well as
, as well as ![]() and
and![]() , excepting for their sign. This property comes out from the Formula [13]
, excepting for their sign. This property comes out from the Formula [13]
![]() (11)
(11)
![]() (12)
(12)
in which the particle velocity ![]() is directed along the axis
is directed along the axis![]() . Both
. Both ![]() and
and ![]() can rise up unlimitedly with an increase of
can rise up unlimitedly with an increase of
![]() (13)
(13)
towards its limit of the light velocity![]() . In effect, in order to satisfy (10) and (7) for arbitrarily large
. In effect, in order to satisfy (10) and (7) for arbitrarily large ![]() and
and![]() , the intervals
, the intervals
![]() (14)
(14)
and
![]() (15)
(15)
entering the (10) and (7) should tend to zero.
But this property has been objected already very soon after the the birth of the Heisenberg uncertainty relations [5] . The objections denying the arbitrary small ![]() and
and ![]() have been raised on both the experimen- tal and theoretical footing [14] - [17] . In fact these references proposed that there exists a minimal
have been raised on both the experimen- tal and theoretical footing [14] - [17] . In fact these references proposed that there exists a minimal ![]() equal to
equal to
![]() (16)
(16)
and a minimal ![]() equal to
equal to
![]() (17)
(17)
where ![]() is the rest mass of a particle.
is the rest mass of a particle.
In order to derive (16) from (8) let us assume that ![]() is the excitation energy of a free particle from the level at
is the excitation energy of a free particle from the level at ![]() to the level of
to the level of![]() . In this case
. In this case
![]() (18)
(18)
where ![]() is the electron momentum.
is the electron momentum.
On the other hand we have
![]() (19)
(19)
which is the effect of one of the Hamilton equations:
![]() (20)
(20)
A transformation of (19) gives
![]() (19a)
(19a)
This formula, substituted together with (18) into (8), gives:
![]() (21)
(21)
or
![]() (21a)
(21a)
Therefore we obtain a condition for the smallest ![]() equal to
equal to
![]() (22)
(22)
This expression differs from (16) solely by a factor of![]() . The smallest
. The smallest![]() , labelled by
, labelled by![]() , is obtained from (22) by requirement that the distance
, is obtained from (22) by requirement that the distance ![]() is travelled with a maximal speed close to
is travelled with a maximal speed close to![]() . Therefore
. Therefore
![]() (23)
(23)
The result in (23) differs from that in (17) solely by the factor of![]() .
.
It can be noted that ![]() in (23) is only a half of the time interval
in (23) is only a half of the time interval
![]() (24)
(24)
required to transform the kinetic energy of a particle motion into the energy of the electromagnetic radiation [18] .
3. Discussion
The lower bounds of ![]() and
and ![]() obtained in (22) and (23) can lead―respectively with the aid of (10) and (8) to the upper bounds of the intervals
obtained in (22) and (23) can lead―respectively with the aid of (10) and (8) to the upper bounds of the intervals ![]() and
and![]() . In particular from (10) and (22) we obtain
. In particular from (10) and (22) we obtain
![]() (25)
(25)
and from (8) and (23):
![]() (26)
(26)
If instead of (8) the Heisenberg uncertainty relation (7) together with (23) is applied, the result for the upper bound of ![]() is
is
![]() (27)
(27)
We see that the Formulae (25)-(27) for the upper bounds of the intervals of momentum and energy approach the relations which are well known from the classical relativistic mechanics. In the present case, however, they are an effect of the quantum-mechanical uncertainty formulae.
If the limiting values ![]() and
and ![]() [see (23) and (26)] are substituted into (8), the uncer-
[see (23) and (26)] are substituted into (8), the uncer-
tainty Relation (8)―in order to be satisfied--should attain its certitude in the form
![]() (8a)
(8a)
for in this case holds the relation
![]() (28)
(28)
If the energy change ![]() is a radiation transfer of energy, so
is a radiation transfer of energy, so
![]() (29)
(29)
there should exist the formula
![]() (30)
(30)
defining a maximal frequency![]() .
.
For ![]() equal to the electron mass
equal to the electron mass ![]() we obtain from (30):
we obtain from (30):
![]() (31)
(31)
Roughly a similar result for ![]() in a metal has been obtained in [10] .
in a metal has been obtained in [10] .
Moreover, for ![]() we have
we have ![]() from (22) and
from (22) and ![]() from (23). The lower limits for the free-electron path and electron transition time in metals calculated before [19] fit the
from (23). The lower limits for the free-electron path and electron transition time in metals calculated before [19] fit the ![]() and
and ![]() quoted above.
quoted above.
If the orbital radii of a hydrogen-like atom having the nucleus of charge ![]() are considered instead of charge
are considered instead of charge ![]() alone, the orbital radii become [20] [21]
alone, the orbital radii become [20] [21]
![]() (32)
(32)
giving the smallest radius ![]()
![]() (32a)
(32a)
According to the result obtained in (22) the smallest possible radius (32) should satisfy the relation
![]() (33)
(33)
This gives a limiting condition for the atomic number
![]() (33a)
(33a)
A similar condition can be obtained by considering the shortest time period ![]() acceptable for the orbit
acceptable for the orbit![]() . In this case from [20] and the result in (22) it should be satisfied
. In this case from [20] and the result in (22) it should be satisfied
![]() (34)
(34)
By applying next the Formula (33a) in (34) we obtain the relation
![]() (35)
(35)
from which, by multiplying the both sides of the last equation in (35) by ![]() and taking into account (32a), we have
and taking into account (32a), we have
![]() (35a)
(35a)
The sense of (35a) is that in order to obtain from (35a) the same limiting ![]() as in (33a) we should assume
as in (33a) we should assume ![]() instead of
instead of ![]() in (32a) as a smallest acceptable distance. This is an expected result if we note that the time formula for
in (32a) as a smallest acceptable distance. This is an expected result if we note that the time formula for ![]() involves necessarily the orbit length
involves necessarily the orbit length ![]() in calculations and not
in calculations and not ![]() alone.
alone.
4. The Uncertainty Relation (8) Referred to the Energy Spectrum of the Hydrogen Atom
Till the present point the electron motion on the orbits has been mainly taken into account. But in calculating the electron transitions between orbits the electron velocity normal to the orbital trajectories has to be considered. Let the electron which is on a circular orbit labelled by![]() , so its radius is defined in (1), be promoted to another orbit, for example
, so its radius is defined in (1), be promoted to another orbit, for example![]() . An effect of this transition is a change of the orbit radius by the amount
. An effect of this transition is a change of the orbit radius by the amount
![]() (36)
(36)
on condition we assume that
![]() (37)
(37)
so the term ![]() can be henceforth neglected. In course of the electron transition we assume that radiation of velocity
can be henceforth neglected. In course of the electron transition we assume that radiation of velocity ![]() is emitted or absorbed. Roughly the time of transition from
is emitted or absorbed. Roughly the time of transition from ![]() to
to ![]() can be estimated by the absolute value of the expression
can be estimated by the absolute value of the expression
![]() (38)
(38)
The property that the time interval ![]() satisfies (38) can be derived from the uncertainty principle (8). In a limiting case of (8) the Formula (8a) is valid from which
satisfies (38) can be derived from the uncertainty principle (8). In a limiting case of (8) the Formula (8a) is valid from which
![]() (39)
(39)
In course of the transition process the electron energy on the orbit is changed by an absolute amount equal to [see (5)]:
![]() (40)
(40)
If we put
![]() (41)
(41)
we obtain from (39) and (40) the formula
![]() (42)
(42)
For large ![]() the time interval
the time interval ![]() is found to be a short amount of the electron circulation time period
is found to be a short amount of the electron circulation time period
![]() (43)
(43)
on the orbit ![]() [20] ;
[20] ;![]() . For from (43) and (42) we have:
. For from (43) and (42) we have:
![]() (44)
(44)
where the factor of 137 is coming from the constant expression (33a).
A characteristic point is that a substitution of ![]() and
and ![]() from (36) and (42), respectively, to the expression of velocity roughly estimated in (38) gives
from (36) and (42), respectively, to the expression of velocity roughly estimated in (38) gives
![]() (45)
(45)
For ![]() and
and ![]() we obtain
we obtain
![]() (45a)
(45a)
The largest velocity (45) coming from ![]() and
and ![]() is
is![]() .
.
If an approximate time interval
![]() (46)
(46)
is substituted in place of ![]() into the Formula (8a) we obtain
into the Formula (8a) we obtain
![]() (47)
(47)
from which
![]() (48)
(48)
This expression becomes equal to that obtained from the Bohr theory in (40) on condition
![]() (49)
(49)
or
![]() (50)
(50)
are satisfied.
In effect a proper choice of ![]() for a given
for a given ![]() provides us with the relation
provides us with the relation
![]() (51)
(51)
Certainly, the ![]() can approach an integer number only at a special
can approach an integer number only at a special![]() .
.
5. The Momentary Force Acting on an Electron in Case of Its Transition between the Orbits
A stationary force acting on the electron of the hydrogen atom is a well-known electrostatic force of the electron attraction by the nucleus. This force is assumed by Bohr to be compensated by the centrifugal force of the electron orbital motion, so on an orbit having the index ![]() the electron is submitted to the force
the electron is submitted to the force
![]() (52)
(52)
Evidently this force is of a stationary character. Our aim is to approach a momentary force acting in course of the electron transition between the orbits.
Since the electron velocity of transition is close to ![]() [see (45)], the electron momentum associated with transition is a product equal approximately to
[see (45)], the electron momentum associated with transition is a product equal approximately to![]() , where
, where ![]() is the electron mass. The momentary force active in a transition from the orbit
is the electron mass. The momentary force active in a transition from the orbit ![]() to another orbit
to another orbit ![]() is
is
![]() (53)
(53)
where the transition time![]() ―assumed to be the time of the action of the force due to the momentum
―assumed to be the time of the action of the force due to the momentum ![]() possessed approximately by the electron―is that calculated in (42). The force obtained in (53) is much larger than (52) because of the ratio
possessed approximately by the electron―is that calculated in (42). The force obtained in (53) is much larger than (52) because of the ratio
![]() (54)
(54)
When the energy relations instead of the forces are taken into account, the force given in (53) is multiplied by the distance ![]() travelled upon it, so the energy of transition is
travelled upon it, so the energy of transition is
![]() (55)
(55)
on condition the velocity property presented in (38) is unchanged. In this case the energy ![]() in (55) is much larger than
in (55) is much larger than ![]() associated with any transition between the electron orbits.
associated with any transition between the electron orbits.
6. Summary
In the first step we have demonstrated on the basis of a modified uncertainty relation between the intervals of energy and time that both an interval of the particle position and that of time can attain some minimal values different than zero. These interval limits differ solely by a factor of ![]() from those predicted a long time ago on both the experimental and theoretical footing [5] -[7] . When applied to the hydrogen-like atom, the lower bounds of the intervals for the position interval and interval of time lead to an upper bound for the atomic number
from those predicted a long time ago on both the experimental and theoretical footing [5] -[7] . When applied to the hydrogen-like atom, the lower bounds of the intervals for the position interval and interval of time lead to an upper bound for the atomic number ![]() equal to 137. On the other hand the upper bounds of the intervals of momentum and energy, obtained from the lower bounds of
equal to 137. On the other hand the upper bounds of the intervals of momentum and energy, obtained from the lower bounds of ![]() and
and![]() , approach the relations which are well known from the classical relativistic mechanics.
, approach the relations which are well known from the classical relativistic mechanics.
A separate attention has been attached to the velocity calculation for the electron transitions between the orbits. First, with the aid of the uncertainty principle, it has been demonstrated that―for the atomic levels having index ![]() equal to about 10―this velocity is very close to the light speed
equal to about 10―this velocity is very close to the light speed![]() . Moreover, the energy changes
. Moreover, the energy changes ![]() which accompany the electron transitions become close to those known from the Bohr’s atomic theory. Such result cannot be obtained from the uncertainty Formula (7).
which accompany the electron transitions become close to those known from the Bohr’s atomic theory. Such result cannot be obtained from the uncertainty Formula (7).
The ratio of the stationary electrostatic force acting on the atomic electron to a momentary force active only in course of the electron transition between the orbits has been estimated in (54).