1. Introduction
In this paper we study a semilinear problem in a fractal domain with semilinear dynamical boundary conditions.
The model problem, we consider can be formally stated as follows:
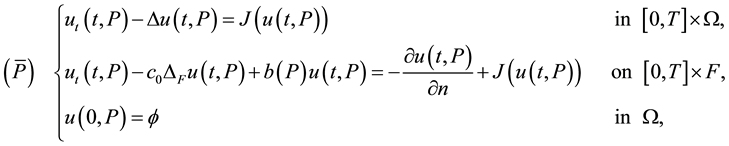
where 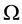 is the (open) snowflake domain and
is the (open) snowflake domain and 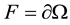 is the union of three Koch curves (see Section 2).
is the union of three Koch curves (see Section 2). 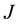 is a non linear function from a subset of
is a non linear function from a subset of 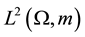 into
into ; m is the sum of the 2-dimensional Lebesgue measure and of the Hausdorff measure of
; m is the sum of the 2-dimensional Lebesgue measure and of the Hausdorff measure of 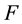 (see Section 2.1).
(see Section 2.1). 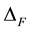 denotes the Laplace operator defined on
denotes the Laplace operator defined on 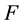 (see (3.4) in Section 3),
(see (3.4) in Section 3), 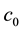 is a positive constant,
is a positive constant, 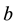 is a strictly positive continuous function
is a strictly positive continuous function
in 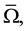
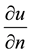 is the normal derivative across
is the normal derivative across 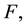 intended in a suitable sense.
intended in a suitable sense.
More precisely, we assume that 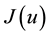 is a non linear mapping from
is a non linear mapping from  to
to ![]() for any fixed
for any fixed ![]() locally Lipschitz i.e. Lipschitz on bounded sets in
locally Lipschitz i.e. Lipschitz on bounded sets in ![]() with Lipschitz constant
with Lipschitz constant ![]() restricted to
restricted to ![]() satisfying a suitable growth condition (see condition (g)) in Section 4). Examples of this type of non linearity include e.g.
satisfying a suitable growth condition (see condition (g)) in Section 4). Examples of this type of non linearity include e.g. ![]() which occurrs in combustion theory (see [1] ) and in the Navier Stokes system (see [2] ).
which occurrs in combustion theory (see [1] ) and in the Navier Stokes system (see [2] ).
Problem ![]() presents a non linear dynamical boundary condition (known also as Venttsel’ boundary condition [3] ). Problem
presents a non linear dynamical boundary condition (known also as Venttsel’ boundary condition [3] ). Problem ![]() models a fluid diffusion within a semipermeable membrane and heat flow subject to non linear cooling on the boundary (see [4] [5] ). The literature on boundary value problems with dynamical conditions is huge, we refer to [6] for a derivation of such boundary conditions and to [7] and the references listed in. All these papers deal with smooth domains. The case of irregular domains is studied in [8] - [12] .
models a fluid diffusion within a semipermeable membrane and heat flow subject to non linear cooling on the boundary (see [4] [5] ). The literature on boundary value problems with dynamical conditions is huge, we refer to [6] for a derivation of such boundary conditions and to [7] and the references listed in. All these papers deal with smooth domains. The case of irregular domains is studied in [8] - [12] .
In the present case we consider the case in which the non linearity appears both in bulk and on the boundary. We study the problem by a semigroup approach. More precisely we consider the corresponding abstract Cauchy problem:
![]() (1.1)
(1.1)
where ![]() is the generator associated to the energy form
is the generator associated to the energy form ![]() introduced in (3.8),
introduced in (3.8), ![]() is a fixed positive real number,
is a fixed positive real number, ![]() is a given function in
is a given function in![]() . We assume that
. We assume that ![]() is a mapping from
is a mapping from ![]() locally Lipschitz i.e. Lipschitz on bounded sets in
locally Lipschitz i.e. Lipschitz on bounded sets in![]() ; we let
; we let ![]() denote the Lipschitz constant of
denote the Lipschitz constant of![]() :
:
![]() (1.2)
(1.2)
whenever![]() .
.
A is the generator of the analytic contraction positivity preserving semigroup ![]() from
from ![]() into
into ![]() associated to
associated to![]() . We study problem
. We study problem ![]() via the corresponding integral equation
via the corresponding integral equation
![]() (1.3)
(1.3)
In order to prove the existence of the solutions to (1.3) the usual way is to use a contraction argument in suitable Banach spaces see e.g. [13] . Usually the functional setting is that of an interpolation space between the domain of the generator ![]() and
and ![]() or the domain of a fractional power of
or the domain of a fractional power of![]() , we refer the reader to [13] - [17] . In our fractal case we do not know the domain of
, we refer the reader to [13] - [17] . In our fractal case we do not know the domain of ![]() We stress the fact that it is not neither known a characterization of the domain of the fractal Laplacian
We stress the fact that it is not neither known a characterization of the domain of the fractal Laplacian ![]() To overcome this difficulty we adapt the abstract approach in [18] to prove local existence and uniqueness results for the mild solution. The key tool in [18] is an assumption on the estimate of the semigroup
To overcome this difficulty we adapt the abstract approach in [18] to prove local existence and uniqueness results for the mild solution. The key tool in [18] is an assumption on the estimate of the semigroup ![]() as a bounded operator from
as a bounded operator from ![]() to
to ![]() (see (2.1) in [18] ). In the present case we take into account that our problem has a probabilistic interpretation [19] ; this, in turn, allows us to deduce an analogue estimate of
(see (2.1) in [18] ). In the present case we take into account that our problem has a probabilistic interpretation [19] ; this, in turn, allows us to deduce an analogue estimate of ![]() as a bounded map from
as a bounded map from ![]() to
to ![]() see (3.15). We then deal with the strong formulation of the B.V.P. satisfied by the mild solution, which is of course of great interest in the applications, actually we prove that the solution of problem
see (3.15). We then deal with the strong formulation of the B.V.P. satisfied by the mild solution, which is of course of great interest in the applications, actually we prove that the solution of problem ![]() solves in a suitable sense Problem
solves in a suitable sense Problem ![]() see Theorems 5.1 and 5.2.
see Theorems 5.1 and 5.2.
The layout of the paper is the following in Section 2 we recall the preliminaries on the geometry and the functional spaces. In Section 3 we consider the energy forms and the associated semigroups. In Section 4 we consider the abstract Cauchy problem ![]() and we prove local and global existence results. Finally in Section 5 we prove that the solution of the abstract Cauchy problem
and we prove local and global existence results. Finally in Section 5 we prove that the solution of the abstract Cauchy problem ![]() solves problem
solves problem ![]() in a suitable sense.
in a suitable sense.
2. Preliminaries
2.1. Geometry
In the paper we denote by ![]() points in
points in![]() , by
, by ![]() the Euclidean distance and by
the Euclidean distance and by ![]() the Euclidean balls. By the Koch snowflake F, we will denote the union of three coplanar Koch curves (see [20] )
the Euclidean balls. By the Koch snowflake F, we will denote the union of three coplanar Koch curves (see [20] )![]() ,
, ![]() and
and ![]() as shown in Figure 1. We assume that the junction points
as shown in Figure 1. We assume that the junction points![]() ,
, ![]() and
and ![]() are the vertices of a regular triangle with unit side length, i.e.
are the vertices of a regular triangle with unit side length, i.e.![]() . From now on we assume that a clockwise orientation is given on
. From now on we assume that a clockwise orientation is given on![]() .
.
The Hausdorff dimension of the Koch snowflake is given by![]() . This fractal is no longer self-similar
. This fractal is no longer self-similar
(and hence, not nested).
One can define, in a natural way, a finite Borel measure ![]() supported on
supported on ![]() by
by
![]() (2.1)
(2.1)
where ![]() denotes the normalized
denotes the normalized ![]() -dimensional Hausdorff measure, restricted to
-dimensional Hausdorff measure, restricted to![]() ,
,![]() .
.
The measure ![]() has the property that there exist two positive constants
has the property that there exist two positive constants![]() ,
, ![]() such that
such that
![]() (2.2)
(2.2)
where ![]() and where
and where ![]() denotes the Euclidean ball in
denotes the Euclidean ball in![]() . As
. As ![]() is supported on
is supported on![]() , it
, it
is not ambiguous to write in (2.2) ![]() in place of
in place of![]() . In the terminology of the following section we say that
. In the terminology of the following section we say that ![]() is a d-set with
is a d-set with ![]() according to [21] .
according to [21] .
Remark 2.1. The Koch snowflake can be also regarded as a fractal manifold (see [22] ).
We denote by ![]() the (open) snowflake domain.
the (open) snowflake domain.
2.2. Functional Spaces
By ![]() we denote the Lebesgue space with respect to the Lebesgue measure
we denote the Lebesgue space with respect to the Lebesgue measure ![]() on subsets of
on subsets of![]() , which will be left to the context whenever that does not create ambiguity. By
, which will be left to the context whenever that does not create ambiguity. By ![]() we denote the Hilbert space of square summable functions on
we denote the Hilbert space of square summable functions on ![]() with respect to the invariant measure
with respect to the invariant measure ![]() Let
Let ![]() be a closed set of
be a closed set of![]() , by
, by ![]() we denote the space of continuous functions on
we denote the space of continuous functions on![]() , by
, by ![]() we denote the space of continuous functions vanishing on
we denote the space of continuous functions vanishing on![]() . Let
. Let ![]() be an open set of
be an open set of![]() , by
, by![]() , where
, where ![]() we denote the usual (possibly fractional) Sobolev spaces (see [23] );
we denote the usual (possibly fractional) Sobolev spaces (see [23] ); ![]() is the closure of
is the closure of![]() , (the infinitely differentiable functions with compact support on
, (the infinitely differentiable functions with compact support on![]() ), with respect to the
), with respect to the ![]() -norm.
-norm.
We now recall a trace theorem.
For ![]() in
in![]() , we put
, we put
![]() (2.3)
(2.3)
at every point ![]() where the limit exists. It is known that the limit (2.3) exists at quasi every
where the limit exists. It is known that the limit (2.3) exists at quasi every ![]() with respect to the
with respect to the ![]() -capacity [24] .
-capacity [24] .
Definition 2.2. Let ![]() be a closed non-empty subset. It is a d-set
be a closed non-empty subset. It is a d-set ![]() if there exists a Borel
if there exists a Borel
measure ![]() with
with ![]() such that for some constants
such that for some constants ![]() and
and ![]()
![]() (2.4)
(2.4)
Such a ![]() is called a d-measure on
is called a d-measure on![]() .
.
Proposition 2.3. The set ![]() is a d-set with
is a d-set with![]() . The measure
. The measure ![]() is a d-measure.
is a d-measure.
See [22] and [25] .
Throughout the paper ![]() will denote possibly different constants.
will denote possibly different constants.
We now come to the definition of the Besov spaces.
Actually there are many equivalent definitions of these spaces see for instance [21] and [26] . We recall here the one which best fits our aims and we will restrict ourselves to the case![]() ,
,![]() ; the general setting being much more involved see [18] . By
; the general setting being much more involved see [18] . By ![]() we denote the space of functions
we denote the space of functions
![]()
where
![]()
Theorem 2.4. Let ![]() then
then ![]() is the trace space to F of
is the trace space to F of ![]() in the following sense:
in the following sense:
1) ![]() is a continuous linear operator from
is a continuous linear operator from ![]() to
to![]() ,
,
2) there is a continuous linear operator ![]() from
from ![]() to
to ![]() such that
such that ![]() is the identity operator in
is the identity operator in![]() .
.
For the proof we refer to Theorem 1 of Chapter VII in [21] , see also [26] .
From now on we denote ![]() by
by![]() .
.
3. Energy Forms and Semigroups Associated
3.1. The Energy Form E
In Definition 4.5 of [22] a Lagrangian measure ![]() on
on ![]() and the corresponding energy form
and the corresponding energy form ![]() as
as
![]() (3.1)
(3.1)
with domain ![]() have been introduced. The domain
have been introduced. The domain![]() , which is a Hilbert space with norm
, which is a Hilbert space with norm
![]() (3.2)
(3.2)
has been characterized in terms of the domains of the energy forms on ![]() (see [22] Theorem 4.6).
(see [22] Theorem 4.6).
In the following we will omit the subscript![]() , the Lagrangian measure will be simply denoted by
, the Lagrangian measure will be simply denoted by ![]() and we will set
and we will set![]() , an analogous notation will be adopted for the energies.
, an analogous notation will be adopted for the energies.
In the following we shall also use the form ![]() which is obtained from
which is obtained from ![]() by the polarization identity:
by the polarization identity:
![]() (3.3)
(3.3)
It can be proved as in Proposition 3.1 of [22] , that:
Proposition 3.1. In the previous notations and assumptions the form ![]() with domain
with domain ![]() is a regular Dirichlet form in
is a regular Dirichlet form in ![]() and the space
and the space ![]() is a Hilbert space under the intrinsic norm (3.2).
is a Hilbert space under the intrinsic norm (3.2).
For the definition and properties of regular Dirichlet forms we refer to [27] . We now define the Laplace operator on![]() . As
. As ![]() is a regular Dirichlet form on
is a regular Dirichlet form on![]() , with domain
, with domain ![]() dense in
dense in![]() , there exists (see Chap. 6, Theorem 2.1 in [28] ) a unique self-adjoint, non positive operator
, there exists (see Chap. 6, Theorem 2.1 in [28] ) a unique self-adjoint, non positive operator ![]() on
on![]() ―with domain
―with domain ![]() dense in
dense in![]() ―such that
―such that
![]() (3.4)
(3.4)
Let ![]() denote the dual of the space
denote the dual of the space![]() . We now introduce the Laplace operator on the fractal
. We now introduce the Laplace operator on the fractal ![]() as a variational operator from
as a variational operator from ![]() by
by
![]() (3.5)
(3.5)
for ![]() and for all
and for all ![]() where
where ![]() is the duality pairing between
is the duality pairing between ![]() and
and![]() . We use the same symbol
. We use the same symbol ![]() to define the Laplace operator both as a self-adjoint operator in (3.4) and as a variational operator in (3.5). It will be clear from the context to which case we refer.
to define the Laplace operator both as a self-adjoint operator in (3.4) and as a variational operator in (3.5). It will be clear from the context to which case we refer.
In the following we denote by
![]() (3.6)
(3.6)
defined in ![]() where
where ![]() denotes a strictly positive continuous function in
denotes a strictly positive continuous function in ![]()
![]() is also a Dirichlet form in
is also a Dirichlet form in ![]()
Consider now the space of functions ![]()
![]() (3.7)
(3.7)
The space ![]() is non trivial. We now introduce the energy form
is non trivial. We now introduce the energy form
![]() (3.8)
(3.8)
defined on the domain![]() . In the following we denote by
. In the following we denote by ![]() the Lesbegue space with respect to the measure
the Lesbegue space with respect to the measure ![]() with
with
![]() (3.9)
(3.9)
By![]() , we will denote the corresponding bilinear form
, we will denote the corresponding bilinear form
![]() (3.10)
(3.10)
defined on![]() .
.
Proposition 3.2. The form ![]() defined in (3.8) is a Dirichlet form in
defined in (3.8) is a Dirichlet form in ![]() and the space
and the space ![]() is a Hilbert space equipped with the scalar product
is a Hilbert space equipped with the scalar product
![]() (3.11)
(3.11)
We denote by ![]() the norm in
the norm in ![]() associated with (3.11) , that is
associated with (3.11) , that is
![]() (3.12)
(3.12)
Resolvents and Semigroups Associated to Energy Forms
As ![]() is a closed bilinear form on
is a closed bilinear form on![]() , with domain
, with domain ![]() dense in
dense in![]() , there exists (see chap. 6 Theorem 2.1 in [28] ) a unique self-adjoint non positive operator
, there exists (see chap. 6 Theorem 2.1 in [28] ) a unique self-adjoint non positive operator ![]() on
on![]() , with domain
, with domain ![]() dense in
dense in![]() , such that
, such that
![]() (3.13)
(3.13)
Moreover in Theorem 13.1 of [27] it is proved that to each closed symmetric form ![]() a family of linear operators
a family of linear operators ![]() can be associated with the property
can be associated with the property
![]()
and this family is a strongly continuous resolvent with generator A, which also generates a strongly continuous semigroup ![]()
With similar arguments it can be proved that there exists a nonnegative self-adjoint operator ![]() with
with
domain ![]() such that
such that ![]()
![]() we denote by
we denote by ![]() the
the
strongly continuous semigroup associated to ![]() on
on ![]()
Proposition 3.3. Let ![]() and
and ![]() be the semigroups generated by the operator A and
be the semigroups generated by the operator A and ![]() respectively, associated to the energy form in (3.13) and in (3.6). Then
respectively, associated to the energy form in (3.13) and in (3.6). Then ![]() and
and ![]() are analytic contraction positive preserving semigroups in
are analytic contraction positive preserving semigroups in ![]() and
and ![]() respectively.
respectively.
Proof. The contraction property follows from Lumer Phillips Theorem on dissipative operators (Chapter 1 Theorem 4.3 in [16] ). In order to prove the analyticity it will be enough to prove that there exists a positive ![]()
such that ![]() (see Proposition 3 Section 6 in Chapter XVII in [29] ). Moreover since
(see Proposition 3 Section 6 in Chapter XVII in [29] ). Moreover since
the semigroup is Markovian it is positive preserving. □
Remark 3.4. It is well known that the symmetric and contraction analytic semigroup ![]() uniquely determines analytic semigroups on the space
uniquely determines analytic semigroups on the space ![]() see (Theorem 1.4.1 [30] ) which we still denote by
see (Theorem 1.4.1 [30] ) which we still denote by ![]() and by
and by ![]() its infinitesimal generator.
its infinitesimal generator.
Let ![]() denote the spectral dimension of
denote the spectral dimension of ![]() [31] [32] . By Theorem B3.7 in [33] one can prove
[31] [32] . By Theorem B3.7 in [33] one can prove
Proposition 3.5. For any ![]()
![]() is a bounded operator and
is a bounded operator and
![]() (3.14)
(3.14)
Proof. The result follows by using the equivalence between (3.14) and Nash inequality. Actually it holds that for any ![]()
![]()
(see [34] ). □
From Theorem 2.11 in [19] the following estimate on the decay of the heat semigroup holds.
Proposition 3.6. There exists a positive constant ![]() such that
such that
![]()
We will consider the case ![]() and
and![]() .
.
We remark that this property is called supercontractivity ( see e.g. [30] ).
From now on we set ![]() for
for ![]()
We recall that for every ![]()
![]() , and
, and
![]()
From interpolation result theory (see e.g. [35] ), it can be proved that for every ![]()
![]()
with
![]() (3.15)
(3.15)
where ![]() and
and ![]()
In particular we will often use that ![]() is bounded from
is bounded from ![]() with
with
![]()
with ![]() and
and ![]()
Taking into account 2.6 and ![]() we obtain
we obtain
![]()
We study the solvability of the Cauchy problem:
![]() (4.1)
(4.1)
where ![]() is the generator associated to the energy form
is the generator associated to the energy form ![]() introduced in (3.8),
introduced in (3.8), ![]() is a fixed positive real number,
is a fixed positive real number, ![]() is a given function in
is a given function in![]() . We assume that
. We assume that ![]() is a mapping from
is a mapping from ![]() locally Lipschitz i.e. Lipschitz on bounded sets in
locally Lipschitz i.e. Lipschitz on bounded sets in![]() ; we let
; we let ![]() denote the Lipschitz constant of
denote the Lipschitz constant of![]() :
:
![]() (4.2)
(4.2)
whenever![]() . We also assume that
. We also assume that![]() . This assumption is not necessary in all that follows but it simplifies the calculations (see [18] ). In order to prove the local existence theorem we make the following assumption on the growth of
. This assumption is not necessary in all that follows but it simplifies the calculations (see [18] ). In order to prove the local existence theorem we make the following assumption on the growth of ![]() when
when ![]()
![]()
we note that ![]() for
for ![]() and
and ![]()
Let![]() . Following the approach in Theorem 2 in [18] and adapting the proof of Theorem 5.1 in [8] we have:
. Following the approach in Theorem 2 in [18] and adapting the proof of Theorem 5.1 in [8] we have:
Theorem 4.1. Let condition (g) hold. Let ![]() be sufficiently small, if
be sufficiently small, if ![]() and
and
![]() (4.3)
(4.3)
There is a ![]() and a unique
and a unique
![]()
with ![]() and
and ![]() satisfying for every
satisfying for every![]() :
:
![]() (4.4)
(4.4)
with the integral being both an ![]() -valued and
-valued and ![]() -valued Bochner integral.
-valued Bochner integral.
The claim of the Theorem is proved by a contraction mapping argument on suitable spaces of continuous functions with values in Banach spaces. We adapt the proof of Theorem 5.1 in [8] to the new functional setting and for the reader’s convenience we recall it.
Proof. Let ![]() be the complete metric space defined as follows
be the complete metric space defined as follows
![]() (4.5)
(4.5)
equipped with the metric
![]()
Since condition (g) holds we choose ![]() such that
such that ![]() for
for ![]()
For![]() , let
, let![]() . By using arguments similar to those used in the proof of Lemma 2.1 of [36] we can prove that
. By using arguments similar to those used in the proof of Lemma 2.1 of [36] we can prove that ![]() and of course
and of course ![]() . We now prove that
. We now prove that
![]() (4.6)
(4.6)
Taking into account (4.3) there exists ![]() such that
such that ![]() for all
for all![]() .
.
![]()
from (4.5) we have that
![]()
where ![]() thus choosing
thus choosing ![]() (4.6) is proved. It remains to prove
(4.6) is proved. It remains to prove
that, for a suitable choice of ![]()
![]() is a contraction.
is a contraction.
![]()
Therefore we have
![]()
We consider now ![]() It holds
It holds
![]()
![]()
In order to prove that it is a contraction it’s enough to choose ![]() such that
such that ![]() and
and
![]() . □
. □
Remark 4.2. If ![]() then
then ![]() Thus condition (g) is satisfied for
Thus condition (g) is satisfied for ![]()
with![]() .
.
Since ![]() is an analytic semigroup on both
is an analytic semigroup on both ![]() and
and ![]() from Corollary 2.1 in [18] , the following regularity result holds (see also Theorem 5.3 in [8] ).
from Corollary 2.1 in [18] , the following regularity result holds (see also Theorem 5.3 in [8] ).
Theorem 4.3. Under the assumptions of Theorem 4.1 we have.
a) The solution ![]() can be continuously extended to a maximal interval
can be continuously extended to a maximal interval ![]() as a solution of (4.4), until
as a solution of (4.4), until![]() .
.
b)
![]()
and satisfies
![]()
i.e. it is a classical solution.
Proof. As to the proof of condition a), we follow Theorem 4.2 in [18] . From the proof of Theorem 4.1 it turns out that the minimum existence time for the solution to the integral equation is as long as ![]() (see also Corollary 2.1. in [18] ).
(see also Corollary 2.1. in [18] ).
To prove that the mild solution is classical we use the classical regularity results for linear equations (see e.g. Theorem 4.3.4. in [13] ) by proving that ![]() is Hölder continuous on
is Hölder continuous on ![]() into
into ![]() for any fixed
for any fixed ![]() Taking into account the local Lipschitz continuity of
Taking into account the local Lipschitz continuity of ![]() it is enough to show that
it is enough to show that ![]() is H
is H![]() continuous on
continuous on ![]() into
into![]() . Let
. Let ![]() we set
we set ![]() if we prove that
if we prove that
![]()
then, as ![]() due to the uniqueness of the solution of (4), then
due to the uniqueness of the solution of (4), then
![]()
for every ![]() hence
hence ![]() is a classical solution (see claim b). Let
is a classical solution (see claim b). Let ![]() Since
Since ![]() is an analytic semigroup,
is an analytic semigroup, ![]() is continuosly differentiable on
is continuosly differentiable on![]() , hence Hölder continuous with any exponent
, hence Hölder continuous with any exponent![]() . It is enough to show that
. It is enough to show that ![]() is Hölder continuous.
is Hölder continuous.
For ![]()
![]() is a bounded operator in
is a bounded operator in ![]() and from Theorem 11.3 and 12.1 in [37] there exists a constant c such that
and from Theorem 11.3 and 12.1 in [37] there exists a constant c such that
![]()
![]()
Now let ![]() then
then
![]()
![]()
Hence,
![]()
If we choose ![]() it follows
it follows ![]() As to the function
As to the function ![]() it holds
it holds
![]()
Hence ![]() Therefore if
Therefore if ![]()
![]() is Hölder continuous on
is Hölder continuous on ![]() with exponent
with exponent![]() . □
. □
We now give a sufficient condition on the initial datum in order to obtain a global solution adapting Theorem 3 (b) in [38] see also Theorem 5.4 in [8] .
Theorem 4.4. Let condition (g) hold. Let ![]()
![]()
![]() a.e. and
a.e. and ![]() is sufficiently small, then there exists a nonnegative
is sufficiently small, then there exists a nonnegative ![]() which is a global solution of (4.4).
which is a global solution of (4.4).
Proof. Since![]() , from (3.15) it follows that
, from (3.15) it follows that ![]() is a bounded operator from
is a bounded operator from ![]() into
into ![]() with
with
![]()
hence
![]()
by choosing ![]() sufficiently small from Theorem 4.1 there exists a local solution of (4.4),
sufficiently small from Theorem 4.1 there exists a local solution of (4.4), ![]() . Furthermore from Theorem 4.1
. Furthermore from Theorem 4.1 ![]() and
and ![]() . From Theorem 4.3 (a) to show that
. From Theorem 4.3 (a) to show that ![]() is a global solution it is enough to show that
is a global solution it is enough to show that ![]() is bounded for every
is bounded for every ![]() We will prove that
We will prove that ![]() is bounded for every
is bounded for every ![]()
and we will use the notations of the proof in Theorem 4.1.
![]()
Let ![]()
![]() is a continuous non decreasing function with
is a continuous non decreasing function with ![]() which satisfies
which satisfies
![]()
if ![]() and
and ![]() then
then ![]() can never equal
can never equal ![]() If it did we would have
If it did we would have ![]() i.e.
i.e. ![]() which is false. This proves that for
which is false. This proves that for ![]() sufficiently small
sufficiently small ![]() must remain bounded. □
must remain bounded. □
5. Strong Interpretation and Regularity Results
Theorem 5.1. Let ![]() be the solution of problem
be the solution of problem![]() . Then we have for every fixed
. Then we have for every fixed ![]()
![]()
and for every ![]()
![]() (5.7)
(5.7)
where![]() , is the inward “normal derivative”, to be defined in a suitable sense. Moreover
, is the inward “normal derivative”, to be defined in a suitable sense. Moreover
![]()
Proof. By proceeding as in Theorem 6.1 of [39] and taking into account that ![]() we obtain for each
we obtain for each ![]()
![]() (5.8)
(5.8)
from this we deduce ![]() and, since the right hand-side belongs to
and, since the right hand-side belongs to ![]() we deduce that
we deduce that ![]() hence
hence
![]()
where
![]()
here the Laplacian is intended in the distributional sense. By proceeding as in (3.26) of [40] [41] we prove that,
for every fixed![]() , the normal derivative
, the normal derivative ![]() is in
is in ![]() the dual of the space
the dual of the space![]() , where
, where ![]() and
and
![]() (5.9)
(5.9)
for every ![]() and every
and every ![]() and by proceeding as in 6.1 of [39] we prove that
and by proceeding as in 6.1 of [39] we prove that
![]() .
.
Let ![]() be an arbitrary function in
be an arbitrary function in![]() , for every fixed
, for every fixed ![]() we multiply Equation (4.1) in
we multiply Equation (4.1) in ![]() and we integrate over
and we integrate over ![]()
![]() (5.10)
(5.10)
the left hand-side of (5.10) can be written as:
![]()
from (3.13) we deduce
![]() (5.11)
(5.11)
![]() (5.12)
(5.12)
taking into account that ![]() from (5.9), we have
from (5.9), we have
![]()
from (5.11) we have
![]()
by proceeding as in Section 6.1 of [39] it can be proved that ![]()
![]()
and the boundary condition holds in ![]() that is
that is
![]() (5.13)
(5.13)
As a consequence of Theorem (5.1) the solution of problem ![]() is the solution of the following problem. For every
is the solution of the following problem. For every![]() ,
,
![]()
Theorem 5.2. Let ![]() be the strict solution of problem
be the strict solution of problem ![]() Then for every
Then for every ![]()
![]()
Proof. For every ![]() we consider the weak solutions
we consider the weak solutions ![]() and
and ![]() of the following auxiliary problems
of the following auxiliary problems
![]() (5.14)
(5.14)
![]() (5.15)
(5.15)
The regularity of ![]() follows from the regularity of
follows from the regularity of ![]() and
and ![]() since
since
![]() (5.16)
(5.16)
We note that for every ![]()
![]()
![]() (see Corollary 3.3 in [42] ) thus in particular
(see Corollary 3.3 in [42] ) thus in particular ![]() Since
Since ![]() is a quasicircle from Theorem 2.7 in [43] it is also a non-tangentially accessible domain (N.T.A.), this implies that it is regular for the Dirichlet problem (5.14) in the sense of Jerison and Kenig (see Definition 2.12 in [43] ); this yields in particular that
is a quasicircle from Theorem 2.7 in [43] it is also a non-tangentially accessible domain (N.T.A.), this implies that it is regular for the Dirichlet problem (5.14) in the sense of Jerison and Kenig (see Definition 2.12 in [43] ); this yields in particular that ![]() As to the regularity of
As to the regularity of ![]() taking into
taking into
account that ![]() from Theorem 1.3 in [44] part B, it follows that
from Theorem 1.3 in [44] part B, it follows that ![]() this concludes
this concludes
the proof.
Acknowledgements
The authors have been supported by the Gruppo Nazionale per l’Analisi Matematica, la Probabilit e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM).