Convergence Theorem of Hybrid Iterative Algorithm for Equilibrium Problems and Fixed Point Problems of Finite Families of Uniformly Asymptotically Nonexpansive Semigroups ()
1. Introduction
Recall the following equilibrium problem. Let  be a closed convex subset of a real Hilbert space
be a closed convex subset of a real Hilbert space  with inner produce
with inner produce  and norm
and norm . Let
. Let  be a bifunction, where
be a bifunction, where 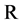 is the set of real numbers. The equilibrium problem for
is the set of real numbers. The equilibrium problem for 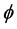 is to to find
is to to find  such that
such that

the set of solutions is denoted by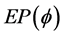 .
.
A mapping  of a normed space
of a normed space  into itself is said to be nonexpansive if
into itself is said to be nonexpansive if  for each
for each . We denote by
. We denote by  the set of fixed point of
the set of fixed point of . Given a mapping
. Given a mapping , let
, let  for all
for all .Then
.Then  if and only if
if and only if  for all
for all , i.e.,
, i.e.,  is a solution of the variational inequality, there are several other problems, for example, the complementarity problem, minimax problems, the Nash equilibrium problem in noncooperative games, fixed point problem and optimization problem, which can also be written in the form of an EP. In other words, the EP is an unifying model for several problems arising in physics, engineering, science, optimization, economics, etc. In the last two decades, many papers have appeared in the literature on the existence of solutions of EP; see, for example ([1] -[3] ) and references therein.
is a solution of the variational inequality, there are several other problems, for example, the complementarity problem, minimax problems, the Nash equilibrium problem in noncooperative games, fixed point problem and optimization problem, which can also be written in the form of an EP. In other words, the EP is an unifying model for several problems arising in physics, engineering, science, optimization, economics, etc. In the last two decades, many papers have appeared in the literature on the existence of solutions of EP; see, for example ([1] -[3] ) and references therein.
Iterative methods for finding fixed points of nonexpansivemappings are an important topic in the theory of nonexpansive mappings and have wide applications in a number of applied areas, such as the convex feasibility problem (see [4] -[7] ), the split feasibility problem (see [8] -[10] ) and image recovery and signal processing (see [6] ).
In 1953, Mann [11] introduced the following iterative process to approximate a fixed point of a nonexpansive single valued mapping  in a Hilbert space
in a Hilbert space :
:

where the initial point  is taken in
is taken in  arbitrarily and
arbitrarily and  is a sequence in
is a sequence in . However, we note that Mann’s iteration process has only weak convergence. To obtain strong converges for Mann iteration, Nakajo and Takahashi [12] and Takahashi et al. [13] introduce some hybrid iterative process. Motivated by Suzuki’s result [14] and Nakajo-Takahashi’s results [12] .
. However, we note that Mann’s iteration process has only weak convergence. To obtain strong converges for Mann iteration, Nakajo and Takahashi [12] and Takahashi et al. [13] introduce some hybrid iterative process. Motivated by Suzuki’s result [14] and Nakajo-Takahashi’s results [12] .
On the other hand, Tada and Takahashi [15] introduce a new iterative method for finding a common element of the set of solutions of an equilibrium problem and the set of fixed points of a nonexpansive mapping T in a Hilbert space H.
A family  of mappings on a closed convex subset
of mappings on a closed convex subset  of a Hibert space
of a Hibert space 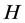 is called a nonexpansive semigroup if it satisfies the following conditions:
is called a nonexpansive semigroup if it satisfies the following conditions:
1)  for all
for all ;
;
2)  for all
for all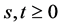 ;
;
3)  for all
for all  and
and 4) for all
4) for all ,
,  is continuous.
is continuous.
Takahashi and Chen [16] proved a strong convergence theorem for nonexpansive semigroups in Hilbert spaces by hybrid method in themathematical programming. Recently Saejung [17] improved the result in [16] .
Takahashi’s result gives us new idea that a finite family of uniformly asymptotically nonexpansive semigroups is introduced.
Definition 1.1 A family  of mappings on a closed convex subset
of mappings on a closed convex subset  of a Hibert space
of a Hibert space  is called an uniformly asymptotically nonexpansive semigroup with sequence
is called an uniformly asymptotically nonexpansive semigroup with sequence  (
(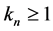 and
and ) if it satisfies the following conditions:
) if it satisfies the following conditions:
1)  for all
for all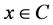 ;
;
2) 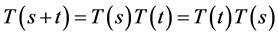 for all
for all ;
;
3)  for all
for all ,
,  ,
, 
4) for all ,
,  is continuous.
is continuous.
In this paper, we introduce a new hybrid iterative process for finding a common element of the set of common fixed points of a finite family of uniformly asymptotically nonexpansive semigroups and the set of solutions of an equilibrium problem in the framework of Hilbert spaces. Then we prove some strong convergence theorems of the proposed iterative process. Our results generalize results of Tada and Takahashi [15] , Takahashi et al. [13] , He and Chen [16] and Saejung [17] .
2. Preliminaries
Throughout the paper, we denote weak convergence of  by
by , and strong convergence by
, and strong convergence by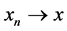 . Let
. Let 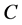 be a closed convex subset of
be a closed convex subset of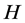 , we use
, we use  to denote the common fixed points set of the semigroup
to denote the common fixed points set of the semigroup
 . i.e.,
. i.e., .
.
Next, We present an example of an uniformly asymptotically nonexpansive semigroup.
Example 2.1 As an example, we consider the nonempty closed convex subset  of a Hilbert space
of a Hilbert space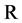 . define
. define . Observe that
. Observe that  is an uniformly asymptotically nonexpansive semigroup.
is an uniformly asymptotically nonexpansive semigroup.
For every point , there exists a unique nearest point in
, there exists a unique nearest point in , denoted by
, denoted by  such that
such that

that is, .
.  is called the metric projection of
is called the metric projection of  onto
onto . It is well known that
. It is well known that  is a nonexpansive mapping. It is also known that H satisfies Opial’s condition, i.e., for any sequence
is a nonexpansive mapping. It is also known that H satisfies Opial’s condition, i.e., for any sequence  with
with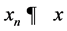 , following the inequality holds:
, following the inequality holds:

To prove our result, we recall the following Lemma.
Lemma 2.1 (see [18] ). Let  be a closed convex subset of
be a closed convex subset of . Given
. Given  and a point
and a point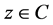 . Then
. Then  if and only if
if and only if  for all
for all .
.
Lemma 2.2 (see [12] ). Let 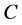 be a closed convex subset of
be a closed convex subset of . Then for all
. Then for all  and
and  we have
we have
 .
.
Lemma 2.3 (see [18] ). Let 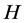 be a real Hilbert space, there hold the following identities:
be a real Hilbert space, there hold the following identities:
1) , for all
, for all  and
and .
.
2) , for all
, for all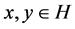 .
.
Lemma 2.4 (see [19] ) Let  be a real Hilbert space. For
be a real Hilbert space. For ,
,

 with
with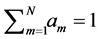 .
.
For solving the equilibrium problem, let us assume the following conditions for a bifunction  (see [1] ):
(see [1] ):
1) , for all
, for all .
.
2) , for all
, for all .
.
3) For each ,
,

4)  is convex and lower semicontinuous for each
is convex and lower semicontinuous for each .
.
Lemma 2.5 (see [1] ) Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and let
and let  be a bifunction of
be a bifunction of  into
into  satisfying (A1)-(A4). Let
satisfying (A1)-(A4). Let  and
and . Then, there exists
. Then, there exists 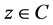 such that
such that

Lemma 2.6 Let 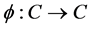 satisfies (A1)-(A4). For
satisfies (A1)-(A4). For 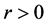 and
and , define a mapping
, define a mapping  as follows:
as follows:
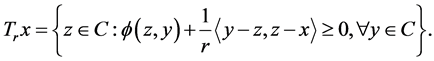
Then, the following holds:
1)  is single valued;
is single valued;
2)  is firmly nonexpansive, i.e., for any
is firmly nonexpansive, i.e., for any ,
, ;
;
3)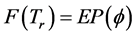 ;
;
4)  is closed and convex.
is closed and convex.
In 2013, Mohammad, E. introduce a new hybrid iterative process for finding a common element of the set of common fixed points of a finite family of nonexpansive semigroups and the set of solutions of an equilibrium problem in the framework of Hilbert spaces. He then prove strong convergence of the proposed iterative process. In this paper, we improve Mohammad’s result, and obtain follwing main results.
Mohammad’s Theorem 3.1 (see [20] ) about nonexpansive semigroups is the special case of our results. Our results improve chang’s result in [21] .
3. Main Results
First, we show the following theorem to our main results.
Theorem 3.1 Let  be nonempty closed convex subset of
be nonempty closed convex subset of .
. 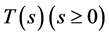 be an uniformly asymptotically nonexpansive semigroups with nonnegative real sequences
be an uniformly asymptotically nonexpansive semigroups with nonnegative real sequences  with
with  and
and  (as
(as ), then
), then  is a closed and convex subset of
is a closed and convex subset of .
.
Proof. Let 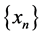 be a sequence in
be a sequence in , such that
, such that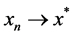 . Since
. Since  be an uniformly asymptotically nonexpansive semigroups, we have
be an uniformly asymptotically nonexpansive semigroups, we have

for  and for all
and for all . Therefore,
. Therefore,

We obtain . Hence,
. Hence, . So, we have
. So, we have . This implies
. This implies 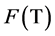 is closed.
is closed.
Let  and
and , and put
, and put . Next we prove that
. Next we prove that . Indeed, in view of Lemma 2.3 2), let
. Indeed, in view of Lemma 2.3 2), let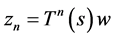 , we have
, we have
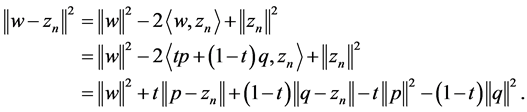 (1)
(1)
Since
 (2)
(2)
Substituting (1) into (2) and simplifying it we have
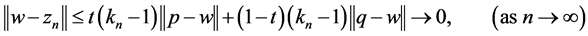
Hence, we have . This implies that
. This implies that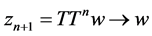 . Since
. Since  is closed, we have
is closed, we have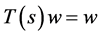 , i.e.,
, i.e.,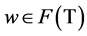 . This completes the proof of theorem 3.1.
. This completes the proof of theorem 3.1.
Theorem 3.2 Let 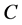 be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  and
and  be a bifunction of
be a bifunction of  into
into  satisfying (A1)-(A4). Let
satisfying (A1)-(A4). Let 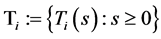
 be a finite family of uniformly asymptotically semigroups with sequence
be a finite family of uniformly asymptotically semigroups with sequence  (
( and
and ). Assume that
). Assume that . For an initial piont
. For an initial piont , let
, let  and
and  be sequences generated by
be sequences generated by
 (3)
(3)
where  is the metric projection of
is the metric projection of  onto
onto . If
. If ,
,  ,
, 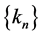 and
and  satisfying the following conditions:
satisfying the following conditions:
1) ;
;
2)  (for
(for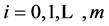 ) and
) and ;
;
3)  and
and ;
;
4) ,
,  then, the sequences
then, the sequences  and
and  converge strongly to
converge strongly to .
.
Proof. 1) First, we prove .
.
Indeed,  is obvious. Suppose that
is obvious. Suppose that , then for
, then for  and
and , by Lemma 2.6 we have
, by Lemma 2.6 we have
 (4)
(4)
Since 
 be a finite family of uniformly asymptotically semigroups,we have
be a finite family of uniformly asymptotically semigroups,we have

which implies that .Therefore we have
.Therefore we have  for all
for all . Note
. Note  is closed and convex.this implies that
is closed and convex.this implies that  is well defined. From Lemma 2.5, sequence
is well defined. From Lemma 2.5, sequence  is also well defined.
is also well defined.
2) Next, we prove that  exists.
exists.
Since 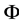 is closed and convex subset of
is closed and convex subset of , there exists a unique
, there exists a unique  such that
such that . From
. From , we have
, we have

Since , we get that
, we get that

It follows that the sequence  is bounded and non decreasing, this implies that
is bounded and non decreasing, this implies that 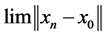 exists
exists
3) Now we show that ,
, .
.
Infact, from Lemma 2.2 we have

witch implies that we get  is Cauchy. Hence there exists
is Cauchy. Hence there exists  such that
such that . Since
. Since , thus
, thus . By Lemma 2.4, we have
. By Lemma 2.4, we have
 (5)
(5)
from condition (C1), so we have

this implies  for all
for all . We know that
. We know that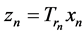 , hence we have
, hence we have

that is,
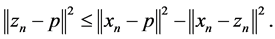
Using  we get that
we get that

that is,

which implies . Hence for all
. Hence for all  we get that
we get that
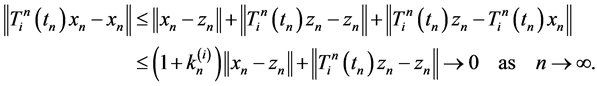
Without loss of generality, as in Saejung’s article [17] , let . For
. For  and
and ,
,

where  denotes the maximal integer that is not larger than
denotes the maximal integer that is not larger than . Since for
. Since for  mapping
mapping 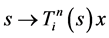 for a fixed
for a fixed 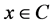 and
and , then
, then .
.
4) Now we prove that .
.
First, since  and
and , by (A2) we get that
, by (A2) we get that

and hence

Since ,
,  and A(4), we get that
and A(4), we get that

If 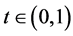 and
and , let
, let , then
, then . So, from (A1)-(A4) we have
. So, from (A1)-(A4) we have

which gives 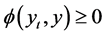 for all
for all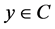 . Hence by (A3) we have
. Hence by (A3) we have

which is .
.
For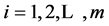 , we have
, we have

Since , then
, then  i.e.,
i.e.,  for all
for all  and thus
and thus .
.
5) Now we prove that .
.
Since  and
and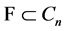 , we get that
, we get that

Since , we have
, we have

which implies . The proof is completed.
. The proof is completed.
From Theorem 3.1, taking 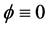 and
and , we obtain Corollary 3.1 Let
, we obtain Corollary 3.1 Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  and
and  be a bifunction of
be a bifunction of  into
into  satisfying (A1)-(A4). Let
satisfying (A1)-(A4). Let 
 be a finite family of uniformly asymptotically semigroups with sequence
be a finite family of uniformly asymptotically semigroups with sequence  (
( and
and ). Assume that
). Assume that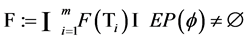 . For an initial piont
. For an initial piont , let
, let  and
and  be sequences generated by
be sequences generated by
 (6)
(6)
where  is the metric projection of
is the metric projection of  onto
onto . If
. If ,
,  ,
,  and
and  satisfying the following conditions:
satisfying the following conditions:
1) ;
;
2)  (for
(for ) and
) and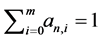 ;
;
3) ,
,  then, the sequences
then, the sequences  converge strongly to
converge strongly to .
.
Competing Interests
The authors declare that they have no competing interests.
Acknowledgements
The authors are very grateful to reviewers for carefully reading this paper and their comments. This work is supported by the Doctoral Program Research Foundation of Southwest University of Science and Technology (No. 11zx7129) and Applied Basic Research Project of Sichuan Province (No. 2013JY0096).
NOTES
*Corresponding author.