Application of the Level Set Method in Three-Dimensional Simulation of the Roughening and Smoothing of Substrates in Nanotechnologies ()
1. Introduction
The surface evolution induced by the ion-bombardment has been subjects of a numerous experimental and theoretical studies in recent years. It was found that the ion sputtering represents one of the crucial processes in producing various nanostructured surfaces or interfaces in nanotechnology [1] -[3] . On the other hand, ion beambased finishing technologies are very important for the surface shape corrections and low-energy ion beams can be beneficially used to tailor the microscopic surface roughness of solid surfaces on a micron and sub-micron scales [4] -[6] .
The control of plasma induced roughness or perhaps control of surface roughness by plasma etching is recognized as one of the limiting and key issues in applications of plasma etching in new generations of plasma technologies [7] [8] . Control of the roughness has become a fast growing area of intensive experimental and theoretical studies. In the majority of such studies, the etching of homogeneous materials with a constant etch rate along the whole volumes has been investigated. However, etched materials, such as nanocomposite materials, usually do not have the same etch rates [7] [8] . The presence of two phases with different etch rates (the ratio of the two etch rates is s and the abundance of one phase is p) strongly affects the formation of the surface roughness and that the etch rate is higher during the isotropic process as compared to the anisotropic process for [7] .
The energetic ions that hit the solids can cause different modifications of the surface topography via opposing effects like surface roughening and surface smoothing [9] [10] . The evolution of the surface caused by the ion bombardment can be described as the interplay between the dynamics of the surface roughening due to sputtering and smoothing due to material transport during surface diffusion. These processes are competitive and responsible for the creation of quasiperiodic ripples [10] and self-affine topographies [11] -[13] . Although there is a large number of studies devoted to ripple formation there are only a few studies on the scaling of the surfaces evolving under ion bombardment [12] -[14] . Among them, [3] [6] [7] [14] deal with surface roughening and [3] [15] involve surface smoothing.
In this paper we present our three-dimensional simulation (3D) results based on the level set method with sparse field method for solving differential equations. We have simulated both the roughness formation during isotropic etching of nanocomposite materials and smoothing of the homogeneous materials.
2. Method
Isotropic etching can be regarded as a non-directional removal of material from a substrate via a chemical process using a corrosive liquid or a plasma. Etchants that are currently used show significant surface roughening, as well as dependence of etching rates on feature density, size, electrical connectivity, and location on the wafer. Smooth etching of silicon applying plasmas is highly desirable for some integrated circuit applications and for manufacturing devices such as microstructures, microsensors, and electro-optic devices. Smooth etching is also advantageous to produce surfaces that will be bonded together, since stronger bonds are formed between flat silicon substrate surfaces having minimum roughness.
Although roughness is usually undesirable, it represents complicated and very expensive to control in manufacturing. Developing integral modeling systems for realistic geometries has evolved into one of the most efficient methods for optimizing plasma processing equipment [16] -[18] . The level set methods are powerful techniques for analyzing and computing moving fronts in a variety of different cases. Level set method has advantages as compared to the other simulation methods since it provides results much faster and with multi scale approach may give local roughness for unlimited resolution. The method have a wide range of applications, including problems in fluid mechanics, combustion, manufacturing of computer chips, computer animation, image processing and many other fields [16] -[18] .
The smoothing process enhanced by the isotropic etching has been modelled for a substrate made of homogenous materials. The obtained simulation results show how properties of material on different scales affect the roughness and smoothing. Analyzing the obtained simulation results, the time dependence of the roughness exponent has been determined for both processes.
In this paper we discuss the application of the level set method for the three-dimensional (3D) modelling of the roughening of the nano-composite surface which characteristics depend not only on the properties of their individual constituents but also on their morphology and interfacial characteristics [7] [8] . We assumed that the nanocomposite materials consist of two phases (polymer and graphite nanoparticles) characterized by the ratio of the two etch rates s = 2 and concentration of the easily etched material p = 0.5. The materials have been randomly distributed and represented by 3D cubic lattice.
3. Simulation Technique and Procedure
The basic idea behind the level set method is to represent the surface in question at a certain time t as the zero level set (with respect to the space variables) of a certain function j(t,x), the so called level set function shown in Figure 1. The initial surface is given by {x|j(0,x) = 0}. The evolution of the surface in time is caused by the surface processes in the case of the etching [19] . The velocity of the point on the surface normal to the surface
will be denoted by R(t,x), and is called velocity function. The velocity function generally depends on the time and space variables and we assume that it is defined on the whole simulation domain. At a later time t > 0, the surface is as well the zero level set of the function j(t,x). Namely, it can be defined as a set of points {x|j(t,x) = 0}. This leads to the level set equation in Hamilton-Jacobi form:
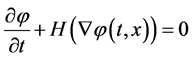 (1)
(1)
in the unknown function j(t,x), where Hamiltonian function is given by H = R(t,x)|Ñφ(t,x)| and where j(0,x) = 0 determines the initial surface. Several approaches for solving level set equations exist which increase accuracy while decreasing computational effort. The most important are narrow band level set method, widely used in etching process modeling tools, and recently developed sparse-filed method [3] . The sparse-field method use an approximation to the level set function that makes it feasible to recompute the neighborhood of the zero level set at each time step. As a result, the number of computations increases with the size of the surface, rather than with the resolution of the grid.
We say that Hamiltonian function H is convex if the following condition is fulfilled:
 (2)
(2)
where  is a partial derivative of φ(t,x) with respect of xi. The non-convex Hamiltonians are characteristic for plasma etching and deposition simulations. During these processes the etching (deposition) rate, that defines the surface velocity function R(t,x), depends on the geometric characteristics of the profile surface itself, or more precisely, on the angle of the incidence of the incoming particles. In the cases under study here we shall consider an etching beam coming down in the vertical direction. These conditions are characteristic for ion milling technology, but angular dependence of the etching rates appears, more or less, in all etching processes. The simplest finite difference scheme that can be applied in these cases is the Lax-Friedrichs scheme, one that relies on the central difference approximation to the numerical flux function, and preserves monotonicity through a secondorder linear smoothing term. It is shown [4] that it is possible to use the Lax-Friedrichs scheme in conjunction with the sparse field method, and to preserve sharp interfaces and corners by optimizing the amount of smoothing in it. This is of special importance in the simulations of the etching processes in which spatially localized effects appear, like notching and microtrenching.
is a partial derivative of φ(t,x) with respect of xi. The non-convex Hamiltonians are characteristic for plasma etching and deposition simulations. During these processes the etching (deposition) rate, that defines the surface velocity function R(t,x), depends on the geometric characteristics of the profile surface itself, or more precisely, on the angle of the incidence of the incoming particles. In the cases under study here we shall consider an etching beam coming down in the vertical direction. These conditions are characteristic for ion milling technology, but angular dependence of the etching rates appears, more or less, in all etching processes. The simplest finite difference scheme that can be applied in these cases is the Lax-Friedrichs scheme, one that relies on the central difference approximation to the numerical flux function, and preserves monotonicity through a secondorder linear smoothing term. It is shown [4] that it is possible to use the Lax-Friedrichs scheme in conjunction with the sparse field method, and to preserve sharp interfaces and corners by optimizing the amount of smoothing in it. This is of special importance in the simulations of the etching processes in which spatially localized effects appear, like notching and microtrenching.
4. Results
The evolution of the surface morphology of nanocomposite material (characterized by the etch rate ratio s = 2 and the abundance of one phase p = 0.5) during isotropic etching is shown in Figure 2. The roughness of a surface exposed to the isotropic etch process increases with processing time evolving from a flat structure to a highly rough structure.


Figure 2. The evolution of the surface roughness during the etching time caused by isotropic etching of a nanocomposite material composed of two phases with the ratio of the etch rates is s = 2 and the abundance of one phase is p = 0.5.
The opposite process involves smoothing of a rough surface as illustrated in Figure 3. Obviously, application of the isotropic etching leads to decreasing the surface roughness over time. As can be noticed, an ideal smooth surface can not be obtained by employing isotropic etch process only.
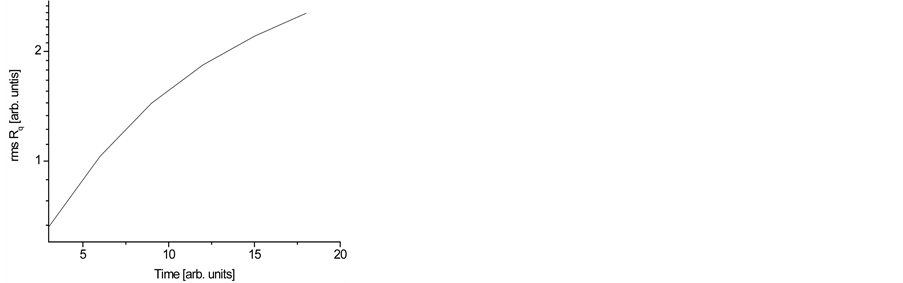
The rms roughness Rq quantifies the surface roughness and is defined as a standard deviation of the height fluctuations along a profile. Figure 4(a) displays the time evolution of the rms roughness Rq illustrating the roughness dynamics. The surface was intentionally roughened by isotropic plasma etching to reach rms value of 2.5. For the roughening, rms roughness Rq changes with the time t according to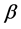 , where
, where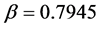 . At the same time, the mean height of the surface during roughening decreases almost monotonically as shown in Figure 4(b). The etching rates can be established from the slope of the curves.
. At the same time, the mean height of the surface during roughening decreases almost monotonically as shown in Figure 4(b). The etching rates can be established from the slope of the curves.
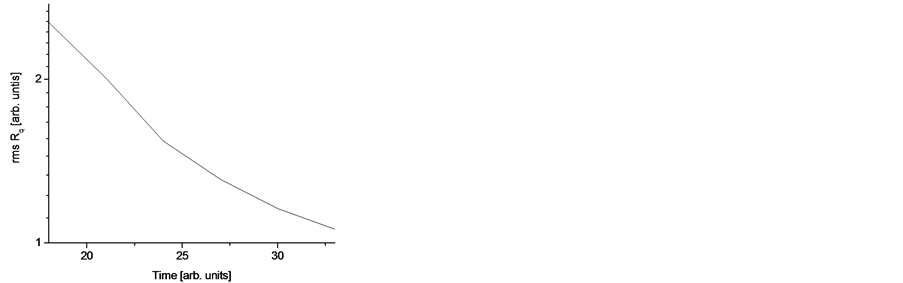
During smoothing process (as can be observed form Figure 5(a) however, the rms roughness Rq decreases from 2.5 to 1.0 indicating that such procedure does not lead to an ideal smooth surface. In that case, the slope of the curve is different and rms roughness Rq also follows 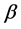 scaling with
scaling with  describing decreasing of the rms roughness Rq. Figure 5(b) shows decreasing of the mean height of the homogenous surface during smoothing processes.
describing decreasing of the rms roughness Rq. Figure 5(b) shows decreasing of the mean height of the homogenous surface during smoothing processes.
5. Conclusions
In this paper we have demonstrated applications of the level set method in performing three-dimensional simulations of the surface topology evolution. Both surface roughening and smoothing processes are simulated. The obtained simulation results indicate that the isotropic etch process has different influences on the surface composed of different materials. The evolution of surface roughness appeared during isotropic etching of material consisting of two randomly distributed phases with different etch rates. On the other hand, surface roughness could be reduced by the isotropic etching.
Explanation can be attributed to the facts that the isotropic etching will attack the substrate made of homogeneous or isotropic materials uniformly in all directions. Concerning the roughness kinetics, the rms Rq dramatically increases in time during roughening. Otherwise rms roughness Rq decreases in the case of smoothing process. Based on the simulation results, the time dependence of the rms Rq has been determined. Simulation results, presented here, apart from their theoretical relevance, have practical implications for surface treatments of various materials.


Figure 3. Images of smoothing of a roughed substrate made of homogeneous materials over the equidistant time intervals during isotropic etch process.
 (a)
(a) (b)
(b)
Figure 4. Dependence of: (a) the rms roughness Ropq and (b) the mean height of tophe surface on etching time of a nanocomposite material characterized by the relative concentration of two phases p = 0.5 and the etch rate ratio s = 2.
 (a)
(a) (b)
(b)
Figure 5. The time evolution of: a) the rms roughness Rq and b) the mean height of the roughed homogenous surface during smoothing process induced by isotropic etching.
Acknowledgements
This study was supported by Grant No. MNTRS141025 from the Ministry of Science of Serbia.