Cosmic Dark Energy from ‘t Hooft’s Dimensional Regularization and Witten’s Topological Quantum Field Pure Gravity ()
1. Introduction
‘t Hooft’s dimensional regularization as well as the role of Einstein’s field equations in connection with quantum particles high energy physics was discussed by the author as well as ‘t Hooft himself on numerous previous occasions [1] -[5] , all a part of the alternatives furnished by different theories employing an inbuilt scale invariance such as fractals and Cantor sets [5] -[7] . Following recent work on clarification of the origin and nature of measurable ordinary energy density accounting for only 4.5% of the total “theoretical” energy density of the universe and the “missing” 95.5% density which are at a minimum we cannot measure directly [9] -[11] , the author realized somewhat belatedly that ‘t Hooft’s renormalization or perhaps more accurately ‘t Hooft-Veltman dimensional regularization procedure offered a neat elegant shortcut derivation of the density of this “missing” dark energy [9] -[11] . It was also at almost the same time or a very short time after that to the author’s own surprise, he realized that the whole subject could be made intimately connected to Witten’s topological field theory and M-theory via an elegantly simple equation connecting the degree of freedom of the graviton in Einstein four and the eleven dimensions of M-theory.
The present work is exclusively devoted to clarifying the above and we will start with dimensional regularization and then proceed from there to the pure gravity Witten theory based solution [12] -[14] .
2. Dark Energy Density from Dimensional Regularization
2.1. ‘t Hooft Dimensional Regularization
Even at the relatively low dimensionality of our classical space when time is fused to it as in Einstein’s general relativity, the Riemannian tensor has 256 components. When all types of symmetries and hidden inter dependence are considered there still remains a substantial number of 20 independent components. One can therefore imagine the intricate role played by dimensions in unification theories. However, it is really the four dimensionality which brings with it more, at least mathematical difficulties than others . Intuitively we could look at this situation as follows: A four dimensional space is neither trivial such as one or two dimensions nor is it sufficiently large to rearrange things in it mathematically speaking. For this and related reasons connected to the disastrous infinities which continuously crop up in quantum field theories and models based on it such as the electroweak theory of Weinberg-Glashow and Salam the requirement of renormalizability is indispensible . It is under these general circumstances that G. ‘t Hooft came with the idea of assuming that spacetime is not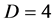 
but 
, where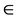 
is a kind of appropriate small order of perturbation parameter and then letting 
tend to zero to restore the integer four dimensionality of spacetime at the end of the conceptually simple but computationally exhausting calculations - . At least initially no one attached any physical interpretation to a fractional topological dimension what so ever. None the less, according to ‘t Hooft his Ph.D. advisor and later on the co-recipient for the Nobel Prize for completing a vital corner of the standard model, M. Veltman occasionally wondered if there could be somewhere a hidden physical meaning for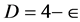 
without letting 
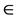go to zero or is dimensional renormalization a purely simple mathematical manoeuvre and no more. ‘t Hooft told the present author what is also reported in that these occasional thoughts got nowhere. However at that time neither fractals were one of the tools of quantum and high energy physicists nor was fractal Cantorian spacetime invented yet. In fact it was in a conference which hosted G. ‘t Hooft that the present author presented a paper published sometime later in the Kluwer-Plenum Proceedings with the title “‘t Hooft’s dimensional regularization implies transfinite Heterotic string theory and dimensional transmutation.” This means in less mystifying learned language, that dimensional regularization implies the fractality of spacetime . Incidentally the first paper in the same volume was by ‘t Hooft and entitled “A Confrontation With Infinity” while the fourth paper was by one of the three main founders of fractal-Cantorian spacetime, Dr. L. Nottale entitled “Scale relativity and non-differentiable fractal spacetime” . The result of the author’s paper at that occasion was to prove the existence of bi-dimensions for fractal spacetime, namely a topological dimension 
and a Hausdorff dimension .
using dimensional regularization. That is how things remained for a short time until it became clear to all working in this field that there are several fundamental dimensions all of which are physically meaningful. Thus we know that spacetime has D = 4 as an expectation value for the topological dimension of what is formally infinite dimensional and hierarchal spacetime with an expectation Hausdorff dimension coupled to it equal 
as well as a third spectral dimension found first by R. Loll and J. Ambjorn equal to D = 4.01999 and finally the electromagnetically entangled dimension 4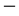
k where 
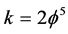and 
is Hardy’s quantum entanglement - . It is this dimension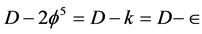 
upon which our derivation of the dark energy density (see Figures 1-3) is based as will be discussed in the next section.
2.2. The Entangled-Fractal 
Spacetime
We know in the meantime quite well that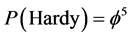 
is a physical fact verified experimentally with high accuracy. It was a result first found by L. Hardy using orthodox quantum mechanics for two quantum particles. Initially it was a gedanken experiment extending Bell’s theorem without inequalities . Hardy did not realize that his probability is golden mean to the power of five until first D. Mermin and later independently the present author developed a general theory of entanglement and connected the entire subject to the Rindler wedge horizon, Unruh temperature and Hawking’s negative vacuum fluctuation . Let us treat dimensions as a pre-particle like states in the spirit of Noether’s theorem and consider their entanglement. Since 
concerns two particles then one dimension would be made smaller by half the quantity of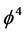 
which means
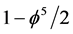. For the four dimensions we have, following volume interpretation of the Hausdorff dimension, a dimension smaller than 4 which we interpret as a quasi Hausdorff dimension because like 
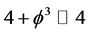it gives us .
To show that this is a solid result of E-infinity spacetime theory - we just need to know that it is part of the Heterotic super string hierarchy obtained by repetitive scaling of 
where 
is the inverse E-infinity electromagnetic fine structure constant and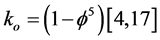 
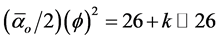
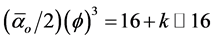
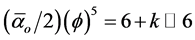
Now the fractal character of DH = 4
k is as clear as its volume interpretation (see Figures 1-3, Table 1 and Flow Chart 1 for further elaboration). It is equally clear that the golden mean Weyl-Nottale scaling is a form of non-standard differentiation of disjointed Cantor sets . How to use this as well as DH to determine the dark energy density is our next task.
2.3. Dark Energy Density and Ordinary Energy Density
Measure theory applied to the problem at hand leads effortlessly to the realization that 
of Einstein is based upon four dimensional volume D = 4 while the transfinite fractal facts all lead to the conclusion that spacetime on extremely small scales of the quantum and by Witten’s T-duality also on the extremely large cosmic scale possesses “fine” structure and a corresponding non-smooth slightly smaller “dimensional volume” equal to 
. Consequently the ratio of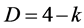 
to that of D = 4 gives us the density of the non-entangled part of spacetime where dark energy lives. Consequently we have
Table 1. Comparison between pure gravity on the one side and E-infinity and noncomputative geometry regarding the meaning of zero set quantum particles and the empty set quantum wave on the other side.
Flow Chart 1. A comparison between two fundamental ways of deducing ordinary energy and dark energy destiny in four main steps.
.
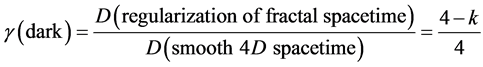This could be looked upon as a scaling exponent (or non-standard substitute to differentiation) and leads via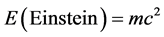 
to
.
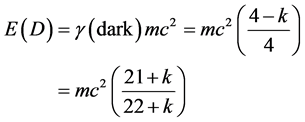Neglecting k = 0.18033989 compared to the integer part in the spirit of ‘t Hooft 
but keeping the difference in mind leads to
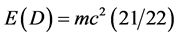
exactly as found previously using numerous different theories where
. To find the “entangled” ordinary energy is relatively a very simple task when realizing that ordinary energy is evidently given by the complimentary Legendre transformation of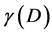 
and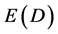
. Consequently ordinary energy density is
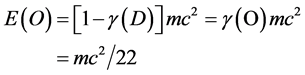
exactly as expected - .
3. Ordinary Energy and Dark Energy from Einstein’s Field Equation for Pure Gravity
In this section we rederive the preceding complimentary densities 
and 
by piecing together ideas due to E. Witten and his school [12] -[14] regarding the field equations of Einstein in the complete absence of a matter field with ideas from noncommutative geometry and fractal-Cantorian spacetime theories [18] -[25] . Naively, it would seem that Einstein’s equation in the absence of a matter field is absolutely trivial and surely without any physical interest. However this seemingly reasonable initial opinion was questioned by many deep thinkers from the earliest of times and led among other things to the work on co-ordinates dependent singularities [10] -[15] . Here the most important aspect of research findings that concerns us is that connected to the topological quantum field theory [12] -[14] . In short like massless gravitons pure gravity has 
degrees of freedom dependent on the dimension d and given by a simple equation which is far from being simple to derive, namely [12] -[14]
.
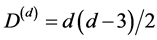Now we make the following observation:
a) for d = 3 we have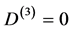 
which implies a quantum-like behaviour or a topological “field” theory [12] -[14] .
b) for d = 2 we have the unintuitive case of negative degrees of freedom 
[12] -[14] . Remarkably for d = 1 we have the same result, i.e.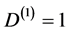
.
c) for relativity d = 4 spacetime we have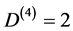 
[12] -[14] . That means that Einstein’s vacuum is a two dimensional string sheet.
d) for the complete unification M-theory d = 11 we have the well known degrees of freedom [12] -[14]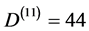 
of a massless graviton [12] .
Recalling what we established in previous numerous publications, namely that the quantum particle may be modelled by the zero set and leads to the entangled and measurable ordinary energy while the quantum wave is modelled by the empty set 
and leads to the dark energy density which we cannot measure, then we could relax our stringent distinction between dimension of degree of freedom and treat them in this case on equal footing so that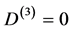 
represents a quantum particle zero set and 
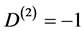as well as 
represents a quantum wave empty set. Consequently the ratios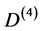 
and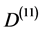 
may be seen as an equivalent substitute to the ratio of 
and 4 or the earlier analysis of Section 2. Consequently 
is in this case found first as
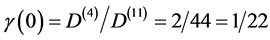
while 
is its Legendre transformation
.
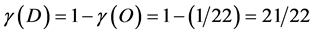In other words, the same results of Section 2 are reproduced using an entirely different method based upon the pure gravity of general relativity [12] -[14] . A comparison between the different theories used in the present work is summarized in Table 1 and Flow Chart 1.
4. Conclusion
What could possibly be the connection between so radically different theories such as dimensional regularization of the electroweak theory of the standard model of high energy physics and the empty field equations of Einstein’s pure gravity as to give exactly the same result for a seemingly distant theory such as that of the cosmological problem of dark energy. The short answer is the geometry and topology of spacetime underlying both theories. We think normally of quantum mechanics as a non-spacetime theory. By contrast all forms of Einstein’s relativity theories are the spacetime theories par excellence. However at grass roots level both theories could be advantageously thought of in terms of a fractal spacetime geometry and topology. We think the present work is an excellent example illustrating the above. There is an almost one to one correspondence between the degrees of freedom of pure gravity for d = 3 and d = 2 as well as d = 1 and the zero set and the empty set of E-infinity Cantorian spacetime theory respectively. The final result is that the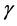 
factor measuring the relative fractality of spacetime could be expressed in terms of the ratio of the two dimensions, namely 4 − k and 4 leading to give 
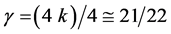or in terms of the degrees of freedom for d = 4 and d = 11, i.e. 
and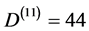
:
Either way the result for the energy density
and
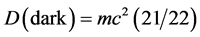
are in astonishing agreement with all the known cosmological measurements of COBE, WMAP, Planck as well as the supernova analysis [8] -[11] [26] [27] . Finally, in view of the above, the author finds it to be justified to call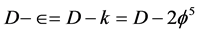 
the Hausdorff dimension of ‘t Hooft-Veltman fractal spacetime.