1. Introduction
Basketball is one of the most popular sports, especially in US, moving a large amount of money. In Brazil, this sport has been achieving increasing proportions mainly with the creation of the NBB (New Brazilian Basketball) in 2009. Basketball is played by two teams with five players each. The winner is the one who gets more points at the end of the match. Draw does not happen due to an overtime whenever there is a draw in the regular time.
The main basketball league is the National Basketball Association (NBA) which has 30 teams divided into two conferences (east and west) of 15 teams, and classified according to their geographical location. Besides the division at conferences, there is a classification into three divisions in each conference with 5 teams in each division, which also uses geographical features to organize the teams. Each team plays 82 games in a season, 41 home matches (in their own stadium) and 41 matches out (in the opponent’s stadium). These 82 games are composed by 4 games against each team of the same division, 3 games against each team that belongs to the same conference, but out of the same division group, 2 games against each team of the other conference and 6 games randomly selected with teams from the other conference. After this initial classification phase, called regular season, the eight best teams (based on number of wins) in each conference qualify to the next phase, called Playoffs, in order to define the season champion.
Due to the popularity of basketball in the US and the increasing values that this sport moves, efficient analysis is always welcome to guide the investments. In the literature, there are many papers using DEA (Data Envelopment Analysis) applied to sports [1] - [4] . Some works use DEA to evaluate the efficiency of basketball players. [5] , for example, uses a procedure that selects non-zero weights in order to evaluate the efficiency of players. [6] also measures the efficiency of players, however, by the cross-efficiency method, considering some environment variables. We found one paper which applies DEA to evaluate NBA basketball teams efficiency proposed by [7] . The authors use a Network DEA approach which consists of five stages, evaluating the performance of first-team and bench-team players, the offensive and defensive systems and the ability for transforming the points made by itself and by the opponents into wins.
In this paper, we propose to evaluate through DEA, teams efficiency of NBA in the seasons 2006-2007, 2007-2008, 2008-2009 and 2009-2010. Thus, teams are the DMUs, the payroll and the average attendance of their home games are the inputs while the number of wins and the average points per game of each team are the outputs. We use the payroll to take into account the investments, average attendance because of the psychological benefit, the number of wins and the average points per game because they measure the success of a team.
First, we calculate teams’ efficiency by the classic BCC output DEA model with the security region that the weights associated with the number of wins are at least two times greater than those associated with the number of points per game. Then, we calculate their cross efficiencies by DEA game to consider that there is no cooperation among DMUs. This approach also improves the discrimination among DMUs.
This paper is divided as follows: Section 2 describes the BCC DEA model used and its results. Section 3 describes how a cross-efficiency can be calculated by DEA game and shows final results by this approach while Section 4 shows the conclusions and the perspectives for future works.
2. DEA BCC
To calculate the efficiency of each team in the NBA basketball seasons 2006-2007, 2007-2008, 2008-2009 and 2009-2010, we use a classical output-oriented DEA BCC with a simple security region. We have, as inputs, team payroll by season and average attendance of home games by season. As outputs, we have number of wins by season and average points per game by season. The security region used is that the weight of output 1 is at least two times greater than the weight of output 2.
For each DMU k (observed DMU), we solved the model (I) to find its efficiency. The mathematical notation used in the model (I) is as follows:
・ 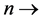 number of DMUs.
number of DMUs.
・ 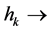 continuous variable that indicates the efficiency of observed DMU k.
continuous variable that indicates the efficiency of observed DMU k.
・ 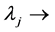 continuous variable that indicates the DMU j contribution for the observed DMU frontier projection (target).
continuous variable that indicates the DMU j contribution for the observed DMU frontier projection (target).
・ 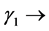 continuous variable associated with the security region constraint.
continuous variable associated with the security region constraint.
・ 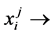 input i value of DMU j.
input i value of DMU j.
・ 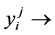 output i value of DMU j.
output i value of DMU j.
(I) max 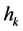 (1.1)
(1.1)
subject to 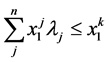 (1.2)
(1.2)
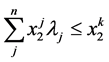 (1.3)
(1.3)
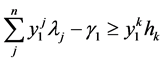 (1.4)
(1.4)
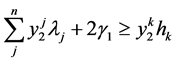 (1.5)
(1.5)
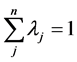 (1.6)
(1.6)
The previous model is known as the envelope model and for each DMU k, allows us to find a whole set of other DMUs called benchmarks set of DMU k. The DMUs belonging to this set are efficient and have similar practices as the DMU k. The set of benchmarks for each DMU is found according to its projection on the efficient frontier. When a DMU is efficient, it is the only benchmark for itself. Mathematically, a DMU j is a benchmark for the DMU k when we run the model (I) for the DMU k and the variable 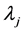 acquires non-null value.
acquires non-null value.
Table 1, Table 2, Table 3 and Table 4 show the results for seasons 2006-2007, 2007-2008, 2008-2009 e 2009-2010, respectively. Table 5 shows for each season, the index of the efficient teams (Table 7 shows the correspondent team of each index). Note that there are a large number of efficient teams in each season. It happens because the BCC model is benevolent. Some teams are efficient in two or more seasons although they do
![]()
Table 1. Efficiency by model (I) for season 2006-2007.
![]()
Table 2. Efficiency by model (I) for season 2007-2008.
not have a high value of outputs, such as team 9 (Grizzlies) and team 14 (Kings). Teams 18 (Mavericks) and 26 (Suns) in the season 2006-2007, 7 (Celtics) and 26 (Suns) in the season 2007-2008, 6 (Cavaliers) and 16 (Lakers) in the season 2008-2009 and 6 (Cavaliers) and 17 (Magic) in the season 2009-2010 are efficient because they have high values of output.
Table 6 shows the number of times each team is a benchmark of other team in each season. Some teams are not showed in the table because they are not a benchmark for any team. Furthermore, when a team is benchmark only once in a season, it means that this team is a benchmark only for itself.
The largest number of times that a team is benchmark is 28. This result is achieved by team 17 (Magic) which is efficient in two seasons and is benchmark for 20 teams in one of them. Team 7 (Celtics) is benchmark 21 times although being efficient in just one season. Another interesting fact is the case of teams 9 (Grizzlies) and 14 (Kings), which despite of being efficient in more than a half of the seasons, the number of times they served as benchmark for other teams is relatively small (13 and 6, respectively). The Grizzlies (Kings) is benchmark just for himself in three of four seasons (two of three seasons) in which it is efficient.
Besides, we also execute the BCC model for a specific case with 120 DMUs, where each team represents a different DMU in each season. Thus, it is possible to make a temporal analysis of each DMU. The results obtained for this case are in Table 7. This table also shows the average efficiency of all seasons dealt in this paper and a ranking related to the average efficiency.
![]()
Table 3. Efficiency by model (I) for season 2008-2009.
In Table 7, 11 DMUs are efficient, where eight of them belong to two last seasons. Besides, the efficiency value always increases for teams 1 (76ers), 24 (Rockets), 25 (Spurs) and 28 (Timberwolves) while the efficiency always decreases for team 10 (Hawks). Team 26 (Suns) is the first of the rank, although it is not efficient in any season. It happens because he has high efficiency values for all the seasons. Despite team 9 (Grizzlies) being efficient in two of the four seasons, it is placed ninth.
We can note that the result of the BCC method leads to a poor discrimination of the efficiencies.
The Classical Cross Efficiency Method
The cross efficiency method [8] is a good way to improve the discrimination among DMUs. For the classical cross efficiency, we first obtain the weights and efficiency of each DMU k by (II). This model is named Multiplier and it is the dual problem of (I). The notation for the model (II) is the following:
・ ![]() number of DMUS
number of DMUS
・ ![]()
![]() number of inputs
number of inputs
・ ![]()
![]() number of outputs
number of outputs
・ ![]() value of the input i for the DMU j.
value of the input i for the DMU j.
・ ![]() value of the output i for the DMU j.
value of the output i for the DMU j.
・ ![]()
![]() weight related to output i
weight related to output i
・ ![]()
![]() weight related to input i
weight related to input i
![]()
Table 4. Efficiency by model (I) for season 2009-2010.
![]()
Table 5. Indexes of efficient teams in each season.
(II) min ![]() (1.7)
(1.7)
Subject to ![]() (1.8)
(1.8)
![]() (1.9)
(1.9)
![]() (1.10)
(1.10)
![]()
Table 6. Number of times that a team is benchmark for each season.
“-”: The team is not efficient.
For each pair of DMUs k and d, we calculate the DMU k efficiency using the weights from DMU![]() . Thus,
. Thus, ![]() is calculated as follows:
is calculated as follows:
![]() (1.11)
(1.11)
The average cross efficiency of DMU k is calculated by the following way:
![]() (1.12)
(1.12)
To avoid ![]() [9] [10] , we add the following group of constraints to model (II):
[9] [10] , we add the following group of constraints to model (II):
![]() (1.13)
(1.13)
It should be noted that with constraint (1.13) the model is no longer BCC, being less benevolent. The efficient frontier may be changed.
Some papers propose secondary objectives in cross efficiency because different weight sets can generate the same efficiency value [8] [11] .
In this paper we apply a cross efficiency method named Dea Game that is not affected by the previous situation. In this method, the weight set of each DMU is obtained iteratively with the constraint that the best efficiency for the others DMUs does not decrease. We describe the method in Section 3.
![]()
Table 7. Teams efficiency by BCC model for all seasons at the same time.
3. DEA Game
In DEA game, proposed by [12] , each DMU is seen as a competitor in an uncooperative environment. In this context, to calculate the cross-efficiency of DMU k related to DMU d, a set of weights is found in order to maximize the efficiency of DMU k with the additional constraint that d efficiency does not decrease. In this context, to calculate the efficiency of each DMU, it is necessary to know the efficiencies of the others, and vice-versa. This problem is solved through an iterative process, where the DMUs efficiencies are found, and these values represent a Nash equilibrium.
Model (III) calculates the cross-efficiency of DMU k related to d with current cross-efficiency ![]() using DEA game.
using DEA game.
(III) min ![]() (1.14)
(1.14)
s.t. ![]() (1.15)
(1.15)
![]() (1.16)
(1.16)
![]() (1.17)
(1.17)
![]() (1.18)
(1.18)
The constraint (1.18) ensures that the efficiency of the DMU d is greater than![]() .
.
Iterative Algorithm 1 describes the steps to find the efficiency of DMUs that represent a Nash equilibrium solution. In this algorithm, ![]() represents the efficiency of DMU j at iteration t.
represents the efficiency of DMU j at iteration t.
Liang et al. [12] proved that the algorithm converges and that the final solution represents a Nash equilibrium.
We apply DEA game for seasons 2006-2007, 2007-2008, 2008-2009 and 2009-2010. The results for each of these seasons are shown in Table 8, Table 9, Table 10 and Table 11, respectively. Those tables show for each season, the BCC efficiencies, the average classical cross-efficiency, DEA game efficiency described in Algorithm 1, rankings associated with the average cross-efficiencies and the DEA game efficiencies along with the difference between these rankings.
Results show a significant difference among the rankings generated by each season of at least 10 units. It is expected since the average cross-efficiency is affected by the multiplicity of optimal weights.
The DEA game is more indicated for noncooperative environment. Besides, it helps differentiating the DMUs, creating a ranking that is not affected by the optimal weights multiplicity. Results concerning this method show that six teams were in three of the four seasons among the top 10 (teams 16, 17, 20, 24, 25 and 26), two teams were among the last ten of all four seasons (teams 8 and 15) and three teams were among the last ten in three of four seasons (teams 5, 14 and 22).
4. Conclusions
In this paper, we show through DEA methodology, classical and cross-efficiency measures of basketball teams belonging to the NBA for 2006-2007, 2007-2008, 2008-2009 and 2009-2010 seasons. In this context, the 30 teams are the DMUs, the two inputs are annual payroll and average attendance at season and outputs 1 and 2 are the number of wins and the average number of points per game, where output 1 has a weight two times higher compared to output 2. For the classical efficiency, we use the BCC method while we use the DEA Game for the cross efficiency.
Regarding teams analysis we can observe Suns is the top ranked because this team has a very high points average and reached a great number of wins. In the last two seasons Cavaliers reached the highest number of wins, but could not achieve the efficiency because of the high investment in payroll and a very high average attendance. The most improved team in our analysis is Charlotte Bobcats which increased a lot the number of wins between seasons 2008-2009 (35 wins) and 2009-2010 (44 wins). Another issue we observed is the benevolence of BCC model which considered Atlanta Hawks and Vancouver Grizzlies as efficient because these teams have the lowest payroll or the lowest average attendance. BCC results showed the efficient teams and benchmarks for each season while DEA Game considered the noncooperative environment, improved the discrimination between the DMUs and gave us a ranking.
In future papers, we intend to deal with the fact that each team belongs to a specific conference and division.
![]()
Table 8. Results summary for the 2006-2007 season.
![]()
Table 9. Results summary for the 2007-2008 season.
![]()
Table 10. Results summary for the 2008-2009 season.
![]()
Table 11. Results summary for the 2009-2010 season.