1. Introduction
The concept of graph tenacity was introduced by Cozzens, Moazzami and Stueckle [1] [2] , as a measure of network vulnerability and reliability. Conceptually graph vulnerability relates to the study of graph intactness when some of its elements are removed. The motivation for studying vulnerability measures is derived from design and analysis of networks under hostile environment. Graph tenacity has been an active area of research since the concept was introduced in 1992. Cozzens et al. in [1] , introduced two measures of network vulnerability termed the tenacity,  , and the Mix-tenacity,
, and the Mix-tenacity,  , of a graph.
, of a graph.
The tenacity  of a graph
of a graph  is defined as
is defined as

where  denotes the order (the number of vertices) of a largest component of
denotes the order (the number of vertices) of a largest component of  and
and  is the number of components of
is the number of components of . A set
. A set  is said to be a
is said to be a  -set of
-set of  if
if
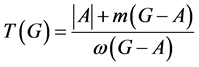 .
.
The Mix-tenacity,  of a graph
of a graph  is defined as
is defined as

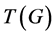 and
and 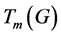 turn out to have interesting properties. Following the pioneering work of Cozzens, Moazzami, and Stueckle, [1] [2] , several groups of researchers have investigated tenacity, and its related problems.
turn out to have interesting properties. Following the pioneering work of Cozzens, Moazzami, and Stueckle, [1] [2] , several groups of researchers have investigated tenacity, and its related problems.
In [3] and [4] Piazza et al. used the Mix-tenacity parameter as Edge-tenacity. This parameter is a combination of cutset  and the number of vertices of the largest component,
and the number of vertices of the largest component, . Also this Parameter didn’t seem very satisfactory for Edge-tenacity, Thus Moazzami and Salehian introduced a new measure of vulnerability, the Edge-tenacity,
. Also this Parameter didn’t seem very satisfactory for Edge-tenacity, Thus Moazzami and Salehian introduced a new measure of vulnerability, the Edge-tenacity,  , in [5] .
, in [5] .
The Edge-tenacity  of a graph
of a graph  is defined as
is defined as

where  denotes the order (the number of edges) of a largest component of
denotes the order (the number of edges) of a largest component of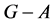 .
.
The concept of tenacity of a graph  was introduced in [1] [2] , as a useful measure of the “vulnerability” of
was introduced in [1] [2] , as a useful measure of the “vulnerability” of . In [6] , we compared integrity, connectivity, binding number, toughness, and tenacity for several classes of graphs. The results suggest that tenacity is the most suitable measure of stability or vulnerability in that for many graphs, and it is the best able to distinguish among graphs that intuitively should have different levels of vulnerability. In [1] [2] [5] -[22] they studied more about this new invariant.
. In [6] , we compared integrity, connectivity, binding number, toughness, and tenacity for several classes of graphs. The results suggest that tenacity is the most suitable measure of stability or vulnerability in that for many graphs, and it is the best able to distinguish among graphs that intuitively should have different levels of vulnerability. In [1] [2] [5] -[22] they studied more about this new invariant.
All graphs considered are finite, undirected, loopless and without multiple edges. Throughout the paper  will denote a graph with vertex set
will denote a graph with vertex set . Further the minimum degree will be denoted
. Further the minimum degree will be denoted , the maximum degree
, the maximum degree , connectivity
, connectivity , the shortest cycle or girth
, the shortest cycle or girth  and we use
and we use  to denote the independence number of
to denote the independence number of  .
.
The genus of a graph is the minimal integer  such that the graph can be drawn without crossing itself on a sphere with
such that the graph can be drawn without crossing itself on a sphere with  handles. Thus, a planar graph has genus 0, because it can be drawn on a sphere without self-crossing. In topological graph theory there are several definitions of the genus of a group. Arthur T. White introduced the following concept. The genus of a group
handles. Thus, a planar graph has genus 0, because it can be drawn on a sphere without self-crossing. In topological graph theory there are several definitions of the genus of a group. Arthur T. White introduced the following concept. The genus of a group 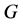 is the minimum genus of a (connected, undirected) Cayley graph for
is the minimum genus of a (connected, undirected) Cayley graph for . The graph genus problem is NP-complete.
. The graph genus problem is NP-complete.
A graph 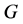 is toroidal if it can be embedded on the torus. In other words, the graphs vertices can be placed on a torus such that no edges cross. Usually, it is assumed that
is toroidal if it can be embedded on the torus. In other words, the graphs vertices can be placed on a torus such that no edges cross. Usually, it is assumed that 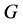 is also non-planar.
is also non-planar.
Proposition 1 (a) If  is a spanning subgraph of
is a spanning subgraph of , then
, then .
.
b) , where
, where .
.
Proposition 2 If 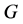 is any noncomplete graph,
is any noncomplete graph, .
.
Proposition 3 If  is a nonempty graph and
is a nonempty graph and  is the largest integer such that
is the largest integer such that  is an induced subgraph of
is an induced subgraph of , then
, then .
.
Corollary 1 a) If  is noncomplete and claw-free the
is noncomplete and claw-free the .
.
b) If  is a nontrivial tree then
is a nontrivial tree then .
.
c) If  is r-regular and r-connected then
is r-regular and r-connected then .
.
The following well-known results on genus will be used.
Proposition 4 If  is a connected graph of genus
is a connected graph of genus , connectivity
, connectivity , girth
, girth , having
, having  vertices,
vertices,  edges and
edges and 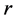 regions, then a)
regions, then a) 
b)  [23]
[23]
c)  [24]
[24]
2. Lower Bound
In this section we establish lower bounds on the tenacity of a graph in terms of its connectivity and genus.
We begin by presenting a theorem due to Schmeichel and Bloom.
Theorem 2.1 (Schmeichel and Bloom [25] ) Let G be a graph with genus . If
. If  has connectivity
has connectivity , with
, with , then
, then

for all 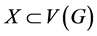 with
with .
.
It is now to drive the bounds on the tenacity that we seek.
Theorem 2.2 If  is a connected graph of genus
is a connected graph of genus  and connectivity
and connectivity , then a)
, then a) , if
, if 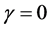 or
or , and b)
, and b) , if
, if .
.
Proof. First, note that the inequalities hold trivially if  or
or . So suppose
. So suppose .
.
First, suppose that . Let
. Let  be a
be a 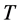 -set. Then since
-set. Then since , by Theorem 2.1 we have
, by Theorem 2.1 we have

So . Since
. Since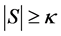 ,
, 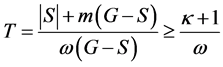 and hence
and hence . Therefore,
. Therefore,

if , we have
, we have  then
then

and part (a) is proved.
So suppose . Again, let
. Again, let  be a
be a  -set in
-set in . Then
. Then
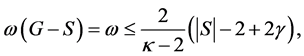
and thus

and  , so
, so
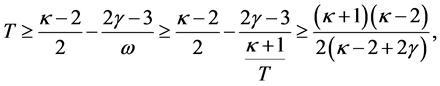
the result follows.
The above bounds is illustrated by a subset of the complete bipartite graph. Let  and
and 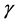 be integer such that
be integer such that  is a multiple of
is a multiple of  and
and . Then
. Then  has connectivity
has connectivity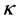 , genus
, genus 
and tenacity .
.
2.1. Planar Graphs and the Lower Bound of Tenacity
We next investigate the bounds provided above if  is a planar or toroidal graph. To this end we require the definition of a Kleetope,
is a planar or toroidal graph. To this end we require the definition of a Kleetope,  , of an embedding
, of an embedding  of a graph. If
of a graph. If  is a graph embedded with regions
is a graph embedded with regions , then
, then  is the graph obtained from
is the graph obtained from  by, for
by, for , inserting a vertex
, inserting a vertex 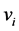 into the interior of
into the interior of 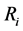 and joining
and joining  to each vertex on the boundary of
to each vertex on the boundary of . Note that the embedding of
. Note that the embedding of 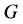 extends naturally to an embedding of
extends naturally to an embedding of . In particular, if
. In particular, if  is a plane graph then so is
is a plane graph then so is . Kleetopes are sometimes used as examples of graphs with maximum independence number for given genus and connectivity (see [26] ).
. Kleetopes are sometimes used as examples of graphs with maximum independence number for given genus and connectivity (see [26] ).
The bound in Theorem 2.2a is not sharp for 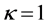 and
and . But the following examples show that the bound is suitable for
. But the following examples show that the bound is suitable for  and all possible values of
and all possible values of . Furthermore, such examples can be obtained with the maximum girth allowed for such connectivity. Note that by proposition 4a, if
. Furthermore, such examples can be obtained with the maximum girth allowed for such connectivity. Note that by proposition 4a, if  is the girth,
is the girth,

Example 1
a) For  the girth can be arbitrarily large. For
the girth can be arbitrarily large. For  consider the graph
consider the graph  obtained by taking
obtained by taking 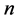 disjoint copies of the path
disjoint copies of the path  on
on  vertices and identifying the corresponding ends into two vertices. This is a planar graph with tenacity
vertices and identifying the corresponding ends into two vertices. This is a planar graph with tenacity  as
as  and girth
and girth .
.
b) For  the girth is at most
the girth is at most . A generalized Herschel graph
. A generalized Herschel graph 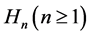 is defined as follows. Form a cyclic chain of 4-cycles by taking
is defined as follows. Form a cyclic chain of 4-cycles by taking  disjoint 4-cycles
disjoint 4-cycles ,
,  , and identifying
, and identifying  and
and 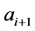 (including
(including  and
and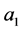 ). Then introduce vertices
). Then introduce vertices  and
and  and make
and make  adjacent to each
adjacent to each 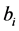 and make
and make  adjacent to each
adjacent to each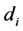 . The result is a 3-connected planar graph of girth 4, (see Figure 1). Now, let
. The result is a 3-connected planar graph of girth 4, (see Figure 1). Now, let  be obtained by replacing each of the
be obtained by replacing each of the  and
and  by dodecahedron as follows. To make notation simpler we explain how to replace a generic node
by dodecahedron as follows. To make notation simpler we explain how to replace a generic node  of degree 3 with a dodecahedron
of degree 3 with a dodecahedron . Suppose the outer cycle of
. Suppose the outer cycle of  is
is  in clockwise order and the neighbors of
in clockwise order and the neighbors of  are
are  and
and  in clockwise order. Then replace
in clockwise order. Then replace  and its incident edges by
and its incident edges by  and the edges
and the edges  and
and . The resulting graph
. The resulting graph  is 3-connected (recall that the dodecahedron is 3-connected), planar, and has girth 5.
is 3-connected (recall that the dodecahedron is 3-connected), planar, and has girth 5.
Furthermore, for 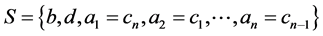 ,
,


Figure 1. Part of the 3- connected planar graph with .
.
while  .
.
c) If  then
then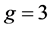 . Let
. Let  be a ladder graph with two rails and
be a ladder graph with two rails and 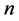 rungs between them. Rails be
rungs between them. Rails be  with vertices
with vertices  and
and  with vertices
with vertices . Now make
. Now make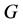 , introduce vertices
, introduce vertices 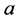 and
and  and make a adjacent to each
and make a adjacent to each  and b adjacent to each
and b adjacent to each .
.  is a planar graph with
is a planar graph with 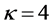 and
and , (see Figure 2). For
, (see Figure 2). For ,
,

whereas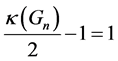 .
.
d) if  then
then . For positive integer
. For positive integer  the graph
the graph 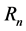 is defined inductively as follows:
is defined inductively as follows:  is a
is a  vertices cycle with
vertices cycle with 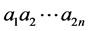 in clockwise order and
in clockwise order and  is a
is a  vertices cycle with
vertices cycle with  in clockwise order.
in clockwise order.
Make two edges between 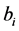 and vertices
and vertices  and
and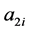 , then introduce
, then introduce  and
and , make edges
, make edges  and
and  (note that
(note that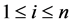 ), in Figure 3 you can see a
), in Figure 3 you can see a  graph with empty cycle vertices as set of
graph with empty cycle vertices as set of  and empty rectangle vertices as set of
and empty rectangle vertices as set of . Suppose that
. Suppose that 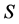 is cut set and
is cut set and , then
, then

whereas  .
.
2.2. Toroidal Graphs
We next consider toroidal graphs in more depth. For  we provide graphs with
we provide graphs with  and maximum girth.
and maximum girth.
Example 2 (a) For  and
and , the family graphs described in Example 1(a) for planar graphs shows that 2-connected graphs can have tenacity arbitrarily close to 1. (Examples specifically with genus 1 can be obtained by adding two edges to
, the family graphs described in Example 1(a) for planar graphs shows that 2-connected graphs can have tenacity arbitrarily close to 1. (Examples specifically with genus 1 can be obtained by adding two edges to , for
, for ).
).
b) For  then
then . The graph
. The graph , for
, for  an even integer has genus 1, connectivity 4,
an even integer has genus 1, connectivity 4,  (since, for example, its bipartite and hamiltonian) and girth 4.
(since, for example, its bipartite and hamiltonian) and girth 4.
c) If 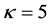 then
then . Consider the following graph
. Consider the following graph 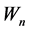 where every region is a pentagon: Let
where every region is a pentagon: Let  and
and 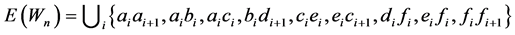 where addition is taken modulo
where addition is taken modulo . The graph
. The graph  is shown in Figure 4.
is shown in Figure 4.
We note that  is toroidal with a pentagonal embedding. Let
is toroidal with a pentagonal embedding. Let . Then
. Then ,
,  ,
,  .
.
d) If  then
then . Consider the cubic bipartite “honeycomb” graph
. Consider the cubic bipartite “honeycomb” graph  on
on 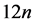 vertices where every region is a hexagon. Then
vertices where every region is a hexagon. Then , satisfies
, satisfies  and
and
 .
.
e) If  then
then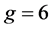 . Consider any (3-connected) bipartite graph
. Consider any (3-connected) bipartite graph 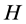 which has partite sets
which has partite sets  and
and  where every vertex in
where every vertex in  has degree 3 and every vertex in
has degree 3 and every vertex in 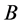 has degree 6 and is embedded in the torus with every region a quadrilateral. For example,
has degree 6 and is embedded in the torus with every region a quadrilateral. For example, . Such an
. Such an  can also be obtained by modifying the honeycomb graph
can also be obtained by modifying the honeycomb graph , depicted in Figure 5 as follows: If the bipartite sets for
, depicted in Figure 5 as follows: If the bipartite sets for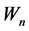 , are
, are  and
and , then add in each region a new vertex and join it to the three vertices of
, then add in each region a new vertex and join it to the three vertices of  on the boundary of the region; the new vertices are added to
on the boundary of the region; the new vertices are added to . Now form
. Now form  by taking
by taking , and replacing every vertex of degree 3 by a dodecahedron as described in Example 1(b). The resulting graph
, and replacing every vertex of degree 3 by a dodecahedron as described in Example 1(b). The resulting graph  satisfies
satisfies ,
,  and
and
 .
.

Figure 2. Part of planar graph with  and
and .
.
The graph  constructed in Example 2(e) has girth
constructed in Example 2(e) has girth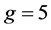 . The lower bound given in Theorem 2.2(b) cannot be obtained if
. The lower bound given in Theorem 2.2(b) cannot be obtained if  and
and  as is shown next.
as is shown next.
Lemma 2.3 If  is a graph with
is a graph with  and
and , then
, then .
.
Proof. Let  be a toroidal graph satisfying the hypothesis of the lemma. Then Euler?s formula (or Proposition 4(a)) shows that the graph is 3-regular. So by Corollary 1(c) the tenacity is at least 1.
be a toroidal graph satisfying the hypothesis of the lemma. Then Euler?s formula (or Proposition 4(a)) shows that the graph is 3-regular. So by Corollary 1(c) the tenacity is at least 1.
3. Conclusions
The sharpness of the bound , if
, if  is illustrated by a subset of the complete bipartite graph. Let
is illustrated by a subset of the complete bipartite graph. Let  and
and 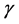 be integer so that
be integer so that  is a multiple of
is a multiple of  and
and . Then
. Then  has connectivity
has connectivity , genus
, genus 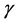 and tenacity
and tenacity . So the bound in Theorem 2.2(b) is attained by an infinite class of graphs, all of girth 4.
. So the bound in Theorem 2.2(b) is attained by an infinite class of graphs, all of girth 4.
The bound in Theorem 2.2(a) is not sharp for  and
and  . But the examples 1 showed that the bound is sharp for
. But the examples 1 showed that the bound is sharp for 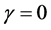 and all possible values of
and all possible values of .
.
For Toroidal graphs when  we introduced graphs with
we introduced graphs with  and maximum girth.
and maximum girth.
Acknowledgements
This work was supported by Tehran University. Our special thanks go to the University of Tehran, College of Engineering and Department of Engineering Science for providing all the necessary facilities available to us for successfully conducting this research. We would like to thank Center of Excellence Geomatics Engineering and Disaster Management for partial support of this research. Also we would like to thank School of Computer Sciences, Institute for Research in Fundamental Sciences (IPM), P.O. Box: 19395-5746, Tehran, Iran, for partial support of this research.
NOTES
*Corresponding author.