1. Introduction
Computing the Cartan invariant matrix  for a finite group of Lie type is an important research subject in the representation theory. One has made many great efforts for this.
for a finite group of Lie type is an important research subject in the representation theory. One has made many great efforts for this.
Firstly, let finite group be of type .
.  for
for  and
and  are treated combinatorially by Alperin [1] [2] and Upadhyaya [3] that almost all Cartan invariants are powers of 2 but some exceptional ones for the form
are treated combinatorially by Alperin [1] [2] and Upadhyaya [3] that almost all Cartan invariants are powers of 2 but some exceptional ones for the form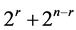 . Benson, Martin [4] and Humphreys [5] exhibit
. Benson, Martin [4] and Humphreys [5] exhibit  for
for  and
and
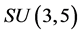 .
.  for
for  is given by Humphreys [6] when
is given by Humphreys [6] when 
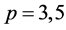 and by Ye [7] when
and by Ye [7] when 
 . Zaslawsky [8] computes
. Zaslawsky [8] computes  for
for  when
when  and for
and for 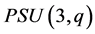 when
when .
.  for
for 
 and
and  is computed by Benson [9] and Du [10] .
is computed by Benson [9] and Du [10] .  for
for 
 has been computed independently by Jantzen (unpublished work) and Ye [11] .
has been computed independently by Jantzen (unpublished work) and Ye [11] .
Secondly, let finite group be of type  and
and . Humphreys [6] and Thackray [12] work out independently
. Humphreys [6] and Thackray [12] work out independently  for
for 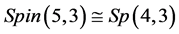
 . Similar computations for
. Similar computations for  are summarized in [13] but
are summarized in [13] but  is not exhibited. Ye [14] , Ye and Zhou [15] , Y. Cheng (unpublished work), Liu and Ye [16] , Hu and Xu [17] compute
is not exhibited. Ye [14] , Ye and Zhou [15] , Y. Cheng (unpublished work), Liu and Ye [16] , Hu and Xu [17] compute  for
for 
 ,
, 
 ,
, 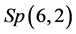 ,
, 
 ,
, 
 , respectively.
, respectively.
At last, let finite group be of type .
.  for
for  has been computed by Mertens [18] when
has been computed by Mertens [18] when  and Hu, Ye [19] when
and Hu, Ye [19] when 
 . In the present note, we shall compute
. In the present note, we shall compute  for the finite group
for the finite group  of type
of type  over a field
over a field  with
with  elements. Some computations involved in this paper were done by using a computer and the MATLAB software. We shall freely use the notations in [15] without further comments.
elements. Some computations involved in this paper were done by using a computer and the MATLAB software. We shall freely use the notations in [15] without further comments.
2. Preliminaries
Let  be a simply-connected semisimple algebraic group of type
be a simply-connected semisimple algebraic group of type  over an algebraically closed field
over an algebraically closed field 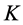 with characteristic
with characteristic . Take a maximal torus
. Take a maximal torus  of
of  such that
such that  is the weight lattice of
is the weight lattice of  with respect to
with respect to . Let
. Let  be the root system associated to
be the root system associated to  with the two simple roots
with the two simple roots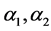 , where
, where  is the long simple root, then
is the long simple root, then  is the set of positive roots, and
is the set of positive roots, and  be root lattice in
be root lattice in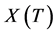 . Let
. Let  be the set of dominant weights with the corresponding fundamental weights
be the set of dominant weights with the corresponding fundamental weights  satisfying
satisfying , and denote by
, and denote by  the weight
the weight  with
with . Then
. Then

It is well known that  with
with  is the Weyl module of the highest weight
is the Weyl module of the highest weight  with the unique simple quotient module
with the unique simple quotient module . In this way,
. In this way,  parameterizes the finite dimensional simple
parameterizes the finite dimensional simple  -modules.
-modules.
Let  denote the scheme-theoretic kernel of the
denote the scheme-theoretic kernel of the  -th Frobenius morphism
-th Frobenius morphism  of
of  and
and  the Frobenius twist for any
the Frobenius twist for any  -module
-module . It is well known that
. It is well known that  is trivial as a
is trivial as a  -module. Moreover, any
-module. Moreover, any  -module that becomes trivial upon restriction to
-module that becomes trivial upon restriction to  is of this form. Let
is of this form. Let
 be the set of restricted dominant weights, then the simple
be the set of restricted dominant weights, then the simple  -modules
-modules ’s with
’s with  remain simple regarded as the
remain simple regarded as the  -modules. On the other hand, any simple
-modules. On the other hand, any simple  - module is isomorphic to exactly one of them. Denote by
- module is isomorphic to exactly one of them. Denote by  the simple
the simple  -modules with
-modules with , whose projective cover is
, whose projective cover is . Then
. Then  is an index set of isomorphic classes of simple
is an index set of isomorphic classes of simple  -modules. Let
-modules. Let  be the finite subgroup consisting of all fixed points of
be the finite subgroup consisting of all fixed points of  in
in , which is called the finite group of type
, which is called the finite group of type . The following facts are well known. For
. The following facts are well known. For , the restriction of the simple
, the restriction of the simple  -module
-module  to
to , denoted by
, denoted by , remains simple. Furthermore, any simple
, remains simple. Furthermore, any simple  -module is isomorphic to exactly one
-module is isomorphic to exactly one  with
with . We denote by
. We denote by  the projective indecomposable
the projective indecomposable
 -module (or
-module (or  -PIM, for short), which has
-PIM, for short), which has  as its top and bottom composition factors.
as its top and bottom composition factors.
Moreover, the restriction  is also a projective
is also a projective 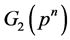 -module and it is decomposed into a direct sum of
-module and it is decomposed into a direct sum of  -PIM’s such that
-PIM’s such that  occurs exactly once.
occurs exactly once. 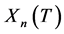 is also an index set of isomorphic classes of simple
is also an index set of isomorphic classes of simple  -modules
-modules  and of projective indecomposable
and of projective indecomposable  -modules
-modules .
.
By the definition, the Cartan invariant  of
of  is the multiplicity of the simple
is the multiplicity of the simple
 -module
-module  occurring as a
occurring as a  -composition factor of the projective indecomposable
-composition factor of the projective indecomposable
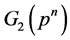 -module
-module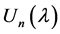 , i.e.
, i.e. . Symmetric matrix
. Symmetric matrix  is called the Cartan invariant matrix, it is of
is called the Cartan invariant matrix, it is of  order.
order.
From now on, we assume . For any
. For any , write
, write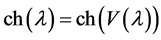 ,
,
 ,
, . And for any
. And for any , write
, write ,
,
 .
.
3. G-Composition Factors of 
Let  be the affine Weyl group of
be the affine Weyl group of , which is generated by all affine reflections
, which is generated by all affine reflections  with
with
 , where
, where  sends
sends  to
to . Dot action
. Dot action  of
of  on
on 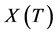
is defined as follows:  for
for  and
and . For this dot action, the origin of
. For this dot action, the origin of  is placed at
is placed at , and
, and  is partitioned into alcoves, whose closures are fundamental domains for the action of
is partitioned into alcoves, whose closures are fundamental domains for the action of  on the euclidean space
on the euclidean space . In case of this paper,
. In case of this paper,  lie in a parallelogram with lowest point
lie in a parallelogram with lowest point  and highest point
and highest point , which is a union of 12 restricted alcoves (see Figure 1). Following [20] , any
, which is a union of 12 restricted alcoves (see Figure 1). Following [20] , any  -translate of this parallelogram is called a “box”; highest point of every box is a special point (intersection of all possible types of affine reflecting hyperplanes). We number some of the dominant alcoves as in Figure 2 for easy reference. We say that an alcove is of type 1 if it is a
-translate of this parallelogram is called a “box”; highest point of every box is a special point (intersection of all possible types of affine reflecting hyperplanes). We number some of the dominant alcoves as in Figure 2 for easy reference. We say that an alcove is of type 1 if it is a  -translate of the alcove marked 1, and so on, for the various restricted alcoves marked 1, 2, 3, 4, 5, 6, 7, 8, 11, 13, 15, 16.
-translate of the alcove marked 1, and so on, for the various restricted alcoves marked 1, 2, 3, 4, 5, 6, 7, 8, 11, 13, 15, 16.
 consists of highest weight
consists of highest weight , weights inside
, weights inside  alcoves and weights on
alcoves and weights on  walls. Let
walls. Let  be any positive integer. We denote by
be any positive integer. We denote by  the set of all weights
the set of all weights  inside the alcove marked
inside the alcove marked . Then weights inside 12 restricted alcoves can be represented as follows:
. Then weights inside 12 restricted alcoves can be represented as follows:
 ;
;
 ;
;
 ;
;
 ;
;
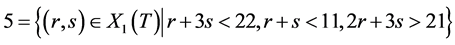 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;

And, we denote by ,
,  ,
,  the sets of all weights on the short right-angled edge, the long right-angled
the sets of all weights on the short right-angled edge, the long right-angled
edge, the incline edge of the right triangle which circles the above marked , respectively, then we can describe weights on
, respectively, then we can describe weights on  walls. For example,
walls. For example,  ,
,  ,
, 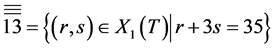 , and so on. It is well known that Weyl group
, and so on. It is well known that Weyl group  of
of  is a Coxeter group generated by
is a Coxeter group generated by  and
and . Write
. Write , then
, then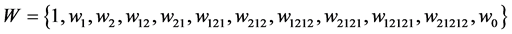 , where
, where . And, the dot action of
. And, the dot action of  on
on  induces the dot action of
induces the dot action of  on
on .
.
 , saying that
, saying that  is linked in
is linked in  means that there exists
means that there exists  such that
such that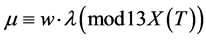 , and write
, and write .
.
Recall some results of Jantzen [21] or Humphreys [22] on the generic decomposition patterns of Weyl modules, limiting ourselves to weights which lie in the lowest  -alcove (an alcove for the affine Weyl group relative to
-alcove (an alcove for the affine Weyl group relative to ). When a dominant weight
). When a dominant weight  lies inside an alcove sufficiently far from the walls of the dominant Weyl chamber, the pattern of
lies inside an alcove sufficiently far from the walls of the dominant Weyl chamber, the pattern of 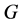 -composition factors of
-composition factors of  depends only on the type of alcove in which
depends only on the type of alcove in which  lies. The corresponding “generic decomposition pattern” consists of the alcoves which contain reflected weights
lies. The corresponding “generic decomposition pattern” consists of the alcoves which contain reflected weights  for which
for which  occurs as a
occurs as a  -composition factor of
-composition factor of ; each such alcove is labelled with the multiplicity of
; each such alcove is labelled with the multiplicity of 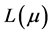 as a
as a  -composition factor. For type
-composition factor. For type  there are 12 type of alcoves, corresponding to the 12 alcoves in the restricted box; hence there are 12 generic patterns. In particular, all patterns involve the same number of alcoves and the same distribution of multiplicities. For type
there are 12 type of alcoves, corresponding to the 12 alcoves in the restricted box; hence there are 12 generic patterns. In particular, all patterns involve the same number of alcoves and the same distribution of multiplicities. For type  the total number of composition factors is 119. Figure 3 shows generic decomposition pattern of
the total number of composition factors is 119. Figure 3 shows generic decomposition pattern of  with
with  lying inside alcove of type 1. Here the bold alcove marked
lying inside alcove of type 1. Here the bold alcove marked  means the alcove in which the highest weight of
means the alcove in which the highest weight of  lies, and
lies, and 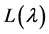 appears once as
appears once as  -composition factor of
-composition factor of , other alcoves marked digits 1 to 4 refer to those alcoves in which the remaining
, other alcoves marked digits 1 to 4 refer to those alcoves in which the remaining  -composition factors
-composition factors ’s with the corresponding multiplicities 1 to 4 of
’s with the corresponding multiplicities 1 to 4 of  except
except  lie.
lie.
Now we determine the  -composition factors of
-composition factors of  with
with . If
. If  lies inside an alcove, we consider each alcove in the generic pattern which lie outside the dominant chamber. Find the special point at the top of the unique box in which that alcove lies. If that point lies on a reflecting hyperplane through
lies inside an alcove, we consider each alcove in the generic pattern which lie outside the dominant chamber. Find the special point at the top of the unique box in which that alcove lies. If that point lies on a reflecting hyperplane through , discard the alcove. Otherwise there is a unique element
, discard the alcove. Otherwise there is a unique element  taking that point to the special point at the top of a box in the dominant chamber. Find the alcove in this box corresponding to the given alcove, and attach to it the multiplicity in the given alcove, with a sign equal to det
taking that point to the special point at the top of a box in the dominant chamber. Find the alcove in this box corresponding to the given alcove, and attach to it the multiplicity in the given alcove, with a sign equal to det . After carrying out this process for all alcoves, and cancelling multiplicities if necessary, the end result is the pattern of
. After carrying out this process for all alcoves, and cancelling multiplicities if necessary, the end result is the pattern of  -composition factors of
-composition factors of  with
with . Figure 4 illustrates this algorithm when
. Figure 4 illustrates this algorithm when  is inside alcove 25 (marked
is inside alcove 25 (marked ) which is of type 11. The two long bold lines indicate the walls of the dominant chamber, i.e.,
) which is of type 11. The two long bold lines indicate the walls of the dominant chamber, i.e.,  -wall and
-wall and  -wall. The bold alcoves marked digits 2, 1, 1, 1, 1, 1, 1 to the right of the
-wall. The bold alcoves marked digits 2, 1, 1, 1, 1, 1, 1 to the right of the  -wall correspond to the dominant alcoves marked digits 4, 3, 3, 3, 2, 1, 2, respectively. A single reflection
-wall correspond to the dominant alcoves marked digits 4, 3, 3, 3, 2, 1, 2, respectively. A single reflection  is involved here, so there are some multiplicity cancellations of alcoves marked digits 4, 3, 3, 3, 2, 1, 2 from the figure. All other alcoves to the right of the
is involved here, so there are some multiplicity cancellations of alcoves marked digits 4, 3, 3, 3, 2, 1, 2 from the figure. All other alcoves to the right of the  - wall disappear, since the special points at the tops of their boxes lie on reflecting hyperplanes through
- wall disappear, since the special points at the tops of their boxes lie on reflecting hyperplanes through . Similarly, The bold alcoves marked digits 1, 1, 1, 1 to the left of the
. Similarly, The bold alcoves marked digits 1, 1, 1, 1 to the left of the  -wall correspond to the dominant alcoves marked digits 4, 3, 3, 3, respectively. A single reflection
-wall correspond to the dominant alcoves marked digits 4, 3, 3, 3, respectively. A single reflection  is involved here, so there are some multiplicity cancellations of alcoves marked digits 4, 3, 3, 3 from the figure. All other alcoves to the left of the
is involved here, so there are some multiplicity cancellations of alcoves marked digits 4, 3, 3, 3 from the figure. All other alcoves to the left of the  -wall also disappear, since the special points at the tops of their boxes lie also on reflecting hyperplanes through
-wall also disappear, since the special points at the tops of their boxes lie also on reflecting hyperplanes through . So the end result is that
. So the end result is that  will have 27
will have 27  -composition factors, corresponding to
-composition factors, corresponding to  inside alcove
inside alcove

Figure 3. General decomposition pattern for alcove of type 1.

Figure 4. Patterns of G-composition factors of alcove 25.
25 and the reflected weights inside alcoves 1, 2, 3, 4, 5, 6, 8, 9, 10, 11, 12(twice), 13, 14(twice), 15, 16, 17(twice), 18, 19, 20, 21, 22, 23, 24.
For a weight  not lying inside an alcove, the
not lying inside an alcove, the  -composition factors of
-composition factors of  are obtained by using Jantzen’s translation principle (cf. [23] ). Find the alcove in whose “upper closure”
are obtained by using Jantzen’s translation principle (cf. [23] ). Find the alcove in whose “upper closure”  lies and compute the pattern as above for an interior weight of this alcove. Then translate all weights involved to the type of wall in which
lies and compute the pattern as above for an interior weight of this alcove. Then translate all weights involved to the type of wall in which  lies; only those in upper closures of alcoves survive to give composition factors of
lies; only those in upper closures of alcoves survive to give composition factors of . For example, when
. For example, when ,
,  will have 13
will have 13  -composition factors, corresponding to
-composition factors, corresponding to  on wall
on wall 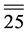 and the reflected weights on walls
and the reflected weights on walls ,
,  ,
,  ,
,  ,
,  (twice),
(twice),  ,
,  ,
,  (twice),
(twice),  ,
, .
.
In particular, we have the following Proposition.
Proposition 3.1 The decomposition patterns of  -composition factors
-composition factors ’s of
’s of  with
with  are listed as follows (Table 1). Here
are listed as follows (Table 1). Here ’s are the reflected weights of
’s are the reflected weights of  under
under .
.
4. Weyl Filtrations of  Module
Module 
Jantzen [24] shows that when , principal indecomposable
, principal indecomposable  -module
-module  admits a
admits a  -module filtration with Weyl
-module filtration with Weyl  -modules as subquotients so called Weyl filtration, and the times of Weyl
-modules as subquotients so called Weyl filtration, and the times of Weyl  -module
-module  appearing as a subquotient in Weyl filtration of
appearing as a subquotient in Weyl filtration of  equals to the multiplicity of the simple
equals to the multiplicity of the simple  -module
-module  occurring as a
occurring as a  -composition factor of Weyl
-composition factor of Weyl  -module
-module , i.e.,
, i.e.,
 . In the case of this paper,
. In the case of this paper, . By a lots of concrete computations, we find that when
. By a lots of concrete computations, we find that when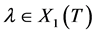 , there are at most 80 dominant alcoves corresponding to the highest weights of Weyl
, there are at most 80 dominant alcoves corresponding to the highest weights of Weyl  -modules occurring as subquotients in Weyl filtration of
-modules occurring as subquotients in Weyl filtration of  with
with , these 80 dominant alcoves are figured in Figure 2. So we can get Weyl
, these 80 dominant alcoves are figured in Figure 2. So we can get Weyl  -modules
-modules ’s occurring as subquotients in Weyl filtration of
’s occurring as subquotients in Weyl filtration of  with
with  from decomposition patterns described in
from decomposition patterns described in . For
. For  lying inside restricted dominant alcoves, we have the following Proposition 4.1.
lying inside restricted dominant alcoves, we have the following Proposition 4.1.
Proposition 4.1 Assume that digit 1 denotes a typical weight inside the alcove 1, digits  denote the reflected weights inside the alcoves
denote the reflected weights inside the alcoves  under W13, then we have the following Table 2. Here the first column denotes the principal indecomposable
under W13, then we have the following Table 2. Here the first column denotes the principal indecomposable  -modules
-modules , the second column denotes the corresponding Weyl Gmodules
, the second column denotes the corresponding Weyl Gmodules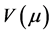 ’s, and n2 means that
’s, and n2 means that  occurs twice.
occurs twice.
Similarly, we can obtain Weyl  -modules
-modules ’s occurring as subquotients in Weyl filtration of
’s occurring as subquotients in Weyl filtration of  with
with  on walls, i.e., upper closures of restricted dominant alcoves.
on walls, i.e., upper closures of restricted dominant alcoves.
For example,  lying inside alcove 16, we can get from the last row of Table 2 that
lying inside alcove 16, we can get from the last row of Table 2 that

and , so we have
, so we have

By Proposition 4.1, we get Weyl  -module
-module ’s decompositions of
’s decompositions of  with
with , and by the methods given in
, and by the methods given in , we obtain
, we obtain  -composition factors of Weyl
-composition factors of Weyl  -module
-module ’s, so we can get all
’s, so we can get all - composition factors of
- composition factors of  with
with . For example
. For example

Table 1. G-composition factors L(μ)’s of .
.

5.  -Composition Factors of
-Composition Factors of 
Let  be the set of all weights of
be the set of all weights of  for
for , and
, and  for
for , i.e., the multiplicity of
, i.e., the multiplicity of  in
in . Some values of
. Some values of  are determined in Table 3, where the first row contains the weights
are determined in Table 3, where the first row contains the weights  each of which labels the corresponding column, and the first column contains the wights
each of which labels the corresponding column, and the first column contains the wights  each of which labels the corresponding row. The number lying in the intersection of the
each of which labels the corresponding row. The number lying in the intersection of the 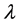 -row and
-row and  -column is just
-column is just .
.
For , let
, let , then we have
, then we have
 , where
, where  if
if  lie on wall of
lie on wall of  chamber or
chamber or  if
if  do not lie on wall of
do not lie on wall of  chamber and
chamber and . By using Table 3, we have
. By using Table 3, we have , for all
, for all .
.
For , by
, by  and Proposition 4.1, we have
and Proposition 4.1, we have , where
, where ,
,  is the weight linked to
is the weight linked to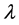 ;
;  and
and . As
. As  -module, we
-module, we
have , so can determine
, so can determine  as follows. In case of this paper,
as follows. In case of this paper, . If
. If , then
, then
 , i.e.,
, i.e.,  , we get all
, we get all  -composition factors of
-composition factors of ; if
; if , which
, which  is maximal one in weights less than
is maximal one in weights less than  linked to
linked to  in
in , then we have
, then we have . But weights less than
. But weights less than  linked to
linked to  in
in  have at most 12, and the Weyl module corresponding to the smallest one is simple. Repeatedly, we have
have at most 12, and the Weyl module corresponding to the smallest one is simple. Repeatedly, we have , where
, where
 .
.
If , then
, then ; if
; if , then
, then ,
,  or
or , so
, so
 , return to the above case. In the end, we have
, return to the above case. In the end, we have
 , where
, where . so determine all
. so determine all  -composition factors
-composition factors ’s
’s  of
of .
.
For example, we have the following expression:

6.  -Decomposition of
-Decomposition of 
For any , restriction of
, restriction of  -module
-module  on
on  is projective
is projective  -module, and can be decomposed into the direct sum of the principal indecomposable
-module, and can be decomposed into the direct sum of the principal indecomposable  -module
-module , Chastkofsky [25] and Jantzen [26] show the decomposition formula, i.e.,
, Chastkofsky [25] and Jantzen [26] show the decomposition formula, i.e.,
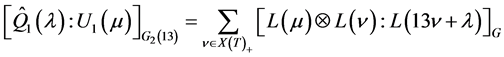
Using this formula and the knowledge of decomposition of tensor products of two simple  -modules in the above section, and by a series of complicated computations, we have the following Proposition 6.1.
-modules in the above section, and by a series of complicated computations, we have the following Proposition 6.1.
Proposition 6.1 The character  of
of  for
for  can be expressed as a sum of character
can be expressed as a sum of character  of
of  with
with  as in the following Table 4.
as in the following Table 4.
By the Proposition 6.1 and the above , we can get all the Cartan invariants of
, we can get all the Cartan invariants of 
 . For example, since
. For example, since , from the above 4.3, we have
, from the above 4.3, we have
 , and so on.
, and so on.
7. Main Results
Let us arrange the row indices from left to right and the column indices from top to bottom in the following order:  for
for  taking
taking , successively;
, successively;
 for
for  taking
taking , successively;
, successively;
 for
for  taking
taking , successively;
, successively;
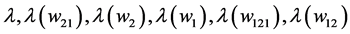 for
for  taking
taking , successively; (12,12). Then, we write the Cartan invariant matrix
, successively; (12,12). Then, we write the Cartan invariant matrix  for the finite group
for the finite group  of type
of type  as
as
 . For convenience, we block
. For convenience, we block  into
into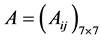 , where
, where  with
with  is square matrix of
is square matrix of  order, and
order, and ,
,  with
with  are
are  matrices, and
matrices, and ,
,  are square matrices of
are square matrices of  order. We list all matrices
order. We list all matrices  in Table 5, where the elements below diagonal are omitted for
in Table 5, where the elements below diagonal are omitted for , the elements above diagonal are omitted for
, the elements above diagonal are omitted for .
.
By MATLAB soft, we have , which is also known by a general result in the representation theory of finite groups on the determinant of the Cartan invariant matrix.
, which is also known by a general result in the representation theory of finite groups on the determinant of the Cartan invariant matrix.
Acknowledgements
The first version of this paper was done during the first named author visited the Abdus Salam International Centre for Theoretical Physics, Trieste, Italy from 1, July, 2009 to 31, August, 2009. He would like to thank the ICTP for the financial support during his stay. He would also like to thank the Commission on Development and Exchanges of the International Mathematical Union for the financial support of the travel expenses in connection with his visiting to the ICTP.
NOTES
*Supported by the Science Foundation for the Excellent Youth Scholars of Henan Province (Grant No. [2005]461).
#Corresponding author.