1. Introduction
An examination is an assessment intended to measure a test-taker’s knowledge, skill, aptitude, physical fitness, or classification in many other topics. Broadly speaking examination can be categorized into standardized and non-standardized (Coelho et al., 2005). Standardized examinations are any examinations that are administered and scored in a consistent manner to ensure legal defensibility. Standardized examinations are fixed in terms of scope, difficulty and format, and are usually significant in consequences (See Linden, 2007; Zucker, 2003). Put differently, standardized examinations are those uniform examinations administered to students from different school districts, counties, and states. Available records show that the origins of standardized examinations can be traced back to the Han period of China based on Confucianism, later consolidated during the Sui period and began to be effective under the Tang Dynasty (Crozier, 2002). The efficacy of standardized examinations has been a subject of ongoing fierce debate pitching the teachers against other groups such as the US Chamber of Commerce and Business Roundtable (Henry, 2007).
Non-standardized examinations are those examinations usually used to determine the proficiency level of students, to motivate students to study, and to provide feedback to students. Teachers grade how they want considering students’ proficiency, attitude, and potential. Non-standardized examinations have been used in its various forms from the origin of mankind. A recent book (Gray, 2013) confirms that even cavemen had their own ways of educating and ensuring their young ones understood their ways of life. For the purposes of this study, the types of examinations administered for undergraduate courses in US colleges are non-standardized examinations. Next, this study presents a brief review of studies on learning outcomes, and the types of examinations administered in US colleges. It discusses the model specifications for the binary logistic regression model, and then shows the estimation and results of the effect of examination policies on students’ learning outcomes.
2. Brief Review of Studies on Learning Outcomes
In the last two decades or so, studies after studies have been pointing to both the declining population with college degrees (Organization for Economic Cooperation and Development, 2005) and the quality of undergraduate education in the United States (National Commission on the Future of Higher Education, 2006). There have been calls for reforms to improve the graduation rates and learning outcomes across universities and colleges in the United States. A critical question that has to be exhaustively addressed has to do with finding out factors that determine learning outcomes in colleges. These studies (Pascarella et al., 1991, 2005) show that, among others, students’ classroom and out-of-class experiences affect learning outcomes.. One study (Kuh, 1993) reports that out-of class experience accounts to70% of students’ learning outcomes. The specific out-of-class experiences that can affect students’ learning outcomes include these (Kuh, 1999): talking with faculty about assignments and career plans; talking with other students about new ideas; making friends from different groups; using information from classes or applying such information to one’s job. Another study (Terenzini et al., 2010) focuses attention on institution factors like how the type of an institution students attend affect their learning outcomes, although these studies (Astin, 1993; Dey et al., 1997) show that institution factor has virtually no effects on learning outcomes once students’ precollege characteristics are controlled, except for the salary and occupational benefits that students derive.
Other studies (Berger et al., 2000) have tended to focus their research attention on an institution’s operational functioning, climate, or culture. However the weakness of the institution-culture factor is that it tended to be distal from students’ learning outcomes. An earlier study (Smart et al., 2000) points to the lack of collaboration between studies on faculty and academic disciplines and those on factors that affect students’ learning outcomes as they pass through college. A notable weakness of most of the studies (Terenzini et al., 2005) is that they fail to incorporate all the factors that affect learning outcomes in colleges. More recently researchers are beginning to focus on closing this missing gap. For example, this study (Terenzini et al., 2007) tests the proposition that internal organizational structures, policies, and faculty culture have more influence on students’ learning outcomes than do such conventional institutional features as type of control, size, wealth, or selectivity. Another recent study (Chen et al., 2008), on faculty members, shows specifically that faculty curricula, policies, and the instructional methods affect students’ learning outcomes; specifically it focuses on how faculty exams affect learning outcomes. There is evidence that faculty grading policy, affecting students’ grade-point average, can be a significant tool in motivating students to learn (Hu et al., 2012).
3. Types of Exams in US Colleges
Examinations in colleges can take a variety of forms. Often instructors adopt a combination of these forms in a particular course. In there are nine possible types of examinations, as follows: (i) In-class: Students are timed and proctored during the examination; (ii) Take-home: Students are allowed to take the examination at home. Note that there are various forms of this type of exam, in terms of submission and timing; (iii) Attendance: Students are assigned some grade points for attendance. (iv) Open questions: Students are given questions or case studies as long as two weeks or more in advance to allow them to prepare answers. (v) Laboratory: Students are required to attend the sessions to complement the knowledge they acquired in another class on the same course. (vi) Online: Students are required to sit in front of a computer at home or the examination center and the questions are presented on the computer monitor and the candidate answers the questions on the computer through the use of mouse. (vii) Open book: Students are allowed to bring books and other material into the examination room. (viii) Projects: Students are given a project individually or in-group and required to research and present or submit a paper based on the research. For the purposes of this study, the above types of examinations (i - viii) are further divided into three, namely (1) traditional (i), (2) nontraditional (ii, iii, iv, v), and (3) project (vi, vii, and viii). In the undergraduate business program under study, the traditional examinations include all tests conducted according to the Student Honor Code having the following features: (i) No student is permitted to have in his possession in the examination room books or paper of any kind except those permitted or given by the proctor or instructor, (ii) No communication among students during the examination is permitted, (iii) No student is permitted to leave the examination room before fifty minutes of the time scheduled for the examination has elapsed. Nontraditional Examination includes take-home, homework, quizzes, laboratory, and take-home coursework. Project includes online examinations (without camera), “project” such as research paper or class presentation.
4. Model Specifications, Data Source, Model Estimation and Results
4.1. Binary Logistic Regression Model
Binary logistic regression is used to model the relationship between a categorical response variable and one or more explanatory variables that may be continuous or categorical. Fundamentally the binary logistic regression model tries to predict which of two possible events, say, yes or no, are going to happen given the information on the explanatory variables (Khan, 2010). The idea is to consider the relationship between the probability of a positive response and the explanatory variables. Because the relationship is non-linear the probability lies between 0 and 1, so linear regression cannot be effective in this instance. The binary logistic regression model can be used to transform such a non-linear to a linear model. The binary logistic model equation can be written as follows:
 (1)
(1)
where Π is the probability of success at covariate level X. This corresponds to the underlying distribution being a binomial distribution and the method used to estimate the parameters of this relationship is that of maximum likelihood. The data are of the form of R positive responses out of N trials. For each trial we assume there is a probability p of a positive response. The distribution of R is the Binomial distribution with parameters N and p. Thus for a particular choice of parameters a and b we can compute the corresponding p for each age group and hence the probability of obtaining the observed values of R. This is called the Likelihood of the data. The “best” choice of a and b is taken to be the values that make the Likelihood a maximum. The binary logistic regression model can be rewritten as follows:
 (2)
(2)
where eβ represents the change in the odds of the outcome by increasing X by 1 unit-oddsratio. That is, every one unit increase in X by 1 unit increases the odds by a factor eβ; β = 0 (eβ =1) è Pr (success) is the same at each level of x; β > 0 (eβ > 1) è Pr (success) increases as x increases; β < 0 (eβ < 1) è Pr (success) decreases as x increases. At 95% Confidence Interval for eβ (odd ratio) the interpretation should be as follows: (i) If interval contains 1, conclude no significant association; (ii) If the interval is above 1, conclude positive association; (iii) If the interval is below 1, conclude negative association. For logistic regression model with multiple covariates the generalized equation can be written as follows:
 (3)
(3)
where log odds are a linear function of the covariates. Once the parameters of the model are estimated the significance of the parameters (certain parameters might be zero) can be tested using the Chi-Squared test:
 (4)
(4)
If the deviance definition of Loss can be used in model fitting a model can be compared by change in Loss. This is also referred to as the Likelihood Ratio Test (LR) as it is equivalent to comparing the models by the ratio of their maximized Likelihood values. Consider binary data with y = 0 or 1, for this:
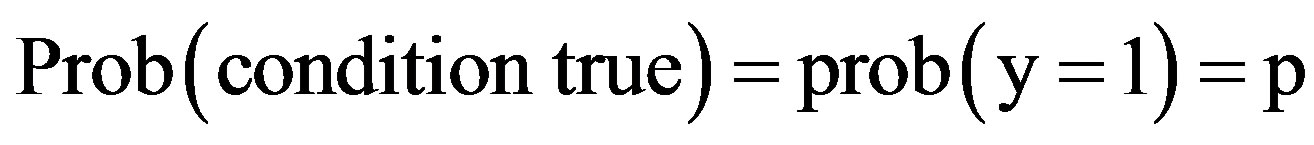 (5)
(5)
In that case the Likelihood for a single observation, y, is p if y = 1 and (1 - p) if y = 0. The deviance then can be expressed conveniently in various ways such as:
 (6)
(6)
An important caution about building a logistic regression model is that there may arise some specification errors. This involves two aspects, on two sides of the logistic regression equation (Bruin, 2006). First, consider the link function of the outcome variable on the left hand side of the equation. The assumption is that the logit function (in logistic regression) is the correct function to use. Secondly, on the right hand side of the equation, the assumption is that all the relevant variables have been included, not included any variables that should not be in the model, and the logit function is a linear combination of the predictors. Thus a specification error may occur if the logit function as the link function is not the correct choice or the relationship between the logit of outcome variable and the independent variables is not linear.
4.2. Data Source
The researcher administered a survey (see Appendix A) to find out from students what type of examinations is the most effective to achieve students’ learning outcomes. In all, one hundred students successfully filled out the survey. The survey results show that majority of the respondents selected the traditional examination (in-class exam) as the most effective in ensuring students’ learning outcomes, followed by nontraditional and the no-exam project, in the second and third places respectively. Then, to find out what types of examinations are predominantly employed by instructors in practice, the researcher identified for this study an undergraduate business program where students are required to take 36 courses to graduate; 32 students who have taken any of the courses provided information on the types of examinations employed by the instructors in the various courses. Upon analyzing the grading policies on the courses, the researcher found that the students who provided the grading information have taken, on average four of the 36 courses; only a handful of the students were final year students who had taken all the courses in the last three years.
4.3. Model Estimation and Results
In this section, this study employs the Stata software to compute the logistic regression based on the instructors’ grade-distribution data on the undergraduate business program. Table 1 shows the same results for the predictors’ p-values, the overall model’s p-value, and the LRchi2 value. The TRADEX has the odds ratio of 11.6. This suggests that there are approximately 12 to 1 odds that traditional examination may improve students’ learning outcomes (STUDLEARN). Also Table 1 shows that both the NONTRDEX and PROJECT have odds ratios of .26 and .85, respectively, meaning by interpretation that there are odds of .26 and .85 to 1 that using NONTRDEX and PROJECT examinations can improve students’ learning outcomes(STUDLEARN). As previously shown in Table 1, the p-value is .000 for the predictor TRADEXAM, meaning that using traditional examination may predict the students’ learning outcomes. The p-value for the overall model is .000, meaning that, jointly, as one, the effects of the three predictors are significant to explaining students’ learning outcomes.
Table 2 shows that the estimated model is correctly classified at approximately 67%. This means that the model (logistic regression) can correctly predict the impacts of examinations on students’ learning outcomes by 67% with a predicted probability of .5 or greater. Of the 1900 grade points assigned to NONTRADEX and PROJECT, the model correctly predicts that 800 grade points would be allocated to TRADEX but 11000 would not. On the other hand, of the 1700 grade points assigned to the TRADEX the model was correct on 1300 grade points.

Table 1. Logistic regression odds ratio.
Note: The dependent variable Y (Studlearn) is the impacts of the three types of examinations on students’ learning outcomes; LR chi 2(3) = 592.02; Prob > chi2 = .0000; Numberofobs. = 3600; Log likelihood = .2193.7631;Pseudo R2 = .1189

Table 2. Results of the percentage of correctly classified.
5. Concluding Remarks
This study has shown that the instructors’ grading policies in an academic program can affect students’ learning outcomes. Evidently, there are three broad types of examinations employed by college instructors, including traditional, nontraditional, and project. Using instructors’ grade compositions in an academic program, the study found the correctly classified estimates of the logistic regression model to be approximately 67%. This means that, comparatively speaking, the majority of the instructors affirmed the traditional examination, requiring proper proctoring of student during examination, as the most effective way to achieving students’ learning outcomes, while nontraditional examination and non-exam project were less effective. Also the researcher conducted a survey (see survey questions in Appendix A) of undergraduate students which showed that majority of the respondents selected the traditional examination. This finding is hardly any major revelation, for there is ample evidence showing that leading education-achieving colleges and nations predominantly adopt traditional examination for undergraduate programs. Suffice it to say that this finding does not in any way imply that the nontraditional and project should be abolished: Both types of examinations can be useful. A reasonable question should be whether or not there can be a particular combination of traditional, nontraditional and project examinations which can generate the most effective students’ learning outcomes? The answer to this question can be deducted by interpreting the correctly classified estimates as follows: All types of examinations being employed by instructors in an academic program, put together, should yield a correctly classified estimate of 50% or above, with the traditional examination being the most prevalent. The following conclusions therefore can be reached, based on the findings. First, an instructor’s examination policy may be less impactful or have negative effects on overall students’ learning outcomes; second, there can be a particular combination of traditional, nontraditional, and project examinations, understood to be the combination of the three types of examinations yielding the highest correctly classified estimates, which can most effectively boost students’ learning outcomes; third, students who participate in an academic program with the higher correctly classified estimates would be expected to have acquired higher learning outcomes than students who participate in a similarly rated academic program with significantly lower correctly classified estimates; fourth, examination policies can be deployed as a critical tool for students’ learning outcomes; and, fifth, a periodic evaluation of examination policies in an academic program may be useful.
Acknowledgements
The author would like to thank professors who participated in the panel discussion when the draft was presented at the 66th New York State Economic Association conference in October, 2013.The author would like to acknowledge the board of directors of the New York Economic Association (NYSEA) for approving the presentation of this paper at the NYSEA 2013 annual conference. The author extends his appreciations to all the students who filled out, helped in administering, and returned the survey forms, and, also, all the students who provided the grade compositions on the courses they took. The author’s gratitude goes to the unanimous reviewers.
Appendix A
Survey On Types Of Exams In College
[1]. Full Name:
[2]. School:
[3]. Major:
[4]. Years (Semesters) already spent in College:
[5]. Please indicate (circle or underline) the types of exams that have been used to test any courses you have taken:
(1) Open-question (ii) Take-home (iii) Quiz (iv) In-class (v) Laboratory (vi) Online
(vii) Open-book (viii) No-exam Project/no-exam presentation (ix) Homework
[6]. Which is the most effective type of exam for testing a course?
(i) Open-question (ii) Take-home (iii) Quiz (iv) In-class (v) Laboratory (vi) Online
(vii) Open-book (viii) No-exam Project/no-exam presentation (ix) Homework
[7]. Use the numbering system, like 1,2,3, 4, & 5, to indicate the 5 most effective ways to test a course material:
(i) Open-question (ii) Take-home (iii) Quiz (iv) In-class (v) Laboratory (vi) Online
(vii) Open-book (viii) No-exam Project/no-exam presentation (ix) Homework
[8]. Which is more effective to ensuring that students better understand a course material?
(a) Open-book (b) In-class
[9]. Which is more effective to ensuring that students better understand a course?
(a) In-class (b) Homework
[10]. Which is more effective to ensuring that students better understand a course?
(a) In-class (b) Quiz
[11]. Which is more effective to ensuring that students better understand a course?
(a) Quiz (b) Laboratory
[12]. Which is more effective to ensuring that students better understand a course?
(a) Laboratory (b) Online
[13]. Which is more effective to ensuring that students better understand a course?
(a) No-exam project/No-exam presentation (b) Quiz
[14]. Which is more effective to ensuring that students better understand a course?
(a) No-exam project/No-exam presentation (b) In-class
[15]. Which is more effective to ensuring that students better understand a course?
(a) Online (b) Quiz
[16]. Which is more effective in ensuring that students better understand a course?
(a) Open-question (b) Online
[17]. Which is more effective to ensuring that students better understand a course?
(a) Open-book (b) In-class
[18]. Which is more effective to ensuring that students better understand a course?
(a) Take-home (b) Online
[19]. Which is more difficult type of exam?
(a) In-class (b) Take-home
[20]. Which is more difficult type of exam?
(a) Homework (b) Take-home
[21]. Which is more difficult type of exam?
(a) In-class (b) Open-book
[22]. Which is more difficult type of exam?
(a) Take-home (b) No-exam project/No-exam presentation
[23]. Which is more difficult type of exam?
(a) Quiz (b) In-class
[24]. Which type of exam should be predominantly used to guarantee the quality of education in college?
(a) Open-book (b) No-exam project/No-exam presentation
(c) In-class (d) Take-home (e) Quiz
[25]. What percent spread (Ex.: 50%, 60%, 70%, 80% etc.) should be assigned to each of the types of exams to guarantee the quality of education (note that the percent spread selected must equal to 100%) in your courses?
(a) Open-book (b) No-exam project/No-exam presentation (c) In-class
(d) Take-home (e) Quiz (f) Online
(g) Open-question (h) Homework