A Neighborhood Condition for Graphs to Have Special [a,b]-Factor ()
Keywords:Graph; Factor; [a,b]-Factor; The Minimum Degree; Neighborhood Condition
1. Introduction
We consider the finite undirected graph without loops and multiple edges. Let  be a graph with vertex set
be a graph with vertex set  and edge set
and edge set  Given
Given , the set of vertices adjacent to
, the set of vertices adjacent to 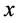 is said to be the neighborhood of
is said to be the neighborhood of , denoted by
, denoted by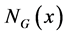 .
.  is called the degree of
is called the degree of  and we write
and we write  for
for
 . Furthermore we define
. Furthermore we define ,
, .
.
For a subset , let
, let  denote the subgraph obtained from
denote the subgraph obtained from 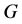 by deleting all the vertices of
by deleting all the vertices of  together with the edges incident with the vertices of
together with the edges incident with the vertices of .
.
Let  and
and  be integers such that
be integers such that . A
. A  factor of
factor of  is defined as a spanning subgraph
is defined as a spanning subgraph  of
of  such that
such that  for all
for all . Other notations and terminology are the same as those in [1]
. Other notations and terminology are the same as those in [1]
The existence of a factor for a graph G is closely related to the degree of vertices. Concerning the minimum degree and the existence of k-factor Egawa, Enomoto [2] and Katerinis [3] proved that there exists k factor when
 and
and  for a graph
for a graph . Iida and Nishimura [4] proved that if
. Iida and Nishimura [4] proved that if 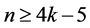 and
and 
there exists k-factor for a graph .
.
H. Y. Pan [5] generalized the result of Iida and Nishimura to [a, b] -factor: if  and
and ,
, 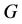 has an
has an  -factor.
-factor.
Concerning adjacent set union and  -factor, in 2000 H. Matsuda gave the following result:
-factor, in 2000 H. Matsuda gave the following result:
Theorem 1 [5]: Let a, b be integer such that , and G be a graph of order
, and G be a graph of order  with
with  and
and .
.
If 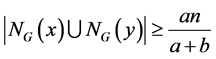 for any two non-adjacent vertices
for any two non-adjacent vertices  and
and 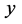 of
of , then
, then  has a
has a 
factor We prove the following theorem for a graph to have a  factor with given properties, which is an extension of theorem 1.
factor with given properties, which is an extension of theorem 1.
Theorem 2: Let  and
and  be integers such that
be integers such that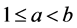 ,
,  be a graph of order
be a graph of order , and
, and  be a subgraph of G with
be a subgraph of G with  edges. If
edges. If , and
, and  for any two non-adjacent vertices
for any two non-adjacent vertices  and
and  of
of , when
, when , we suppose
, we suppose

Then  has a
has a  factor containing all edges of
factor containing all edges of .
.
2. Proof of Theorem 2
Let S and T be two disjoint subset of V(G), E1 and E2 be two disjoint subset of E(G). Let ,
,
 ,
,  ,
, .
.
 ,
, 
 ,
, 
 ,
, 
Lemma 1 [6]: Let  be a graph, and let
be a graph, and let  and
and 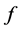 be two integer-valued functions defined on
be two integer-valued functions defined on  such that
such that  for all
for all . Let
. Let  and
and  be two disjoint subsets of
be two disjoint subsets of .
.
Then  has a
has a 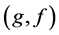 -factor
-factor  such that
such that  and
and  if and only if for any two disjoint subsets
if and only if for any two disjoint subsets  and
and  of
of .
.

Lemma 2: Let  and
and  be integers such that
be integers such that , and
, and  be a graph, and
be a graph, and  be a subgraph of
be a subgraph of
 . Then
. Then  has a
has a  factor
factor 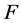 such that
such that  if and only if
if and only if
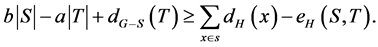
Let  and
and , and we note that
, and we note that

where  and
and .
.
It is easy to see Lemma 2 is an immediately result of Lemma 1.
Now we prove Theorem 2: Suppose that  satisfies the assumptions of Theorem 2, but it has no
satisfies the assumptions of Theorem 2, but it has no  factor as described in Theorem 2. Then by Lemma 2 there exist two disjoint subsets
factor as described in Theorem 2. Then by Lemma 2 there exist two disjoint subsets 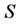 and
and  of
of  such that
such that
 (1)
(1)
We choose such S and  so that
so that  is minimum. If
is minimum. If , then by (1) we get
, then by (1) we get which is a contradiction. Since
which is a contradiction. Since  for all
for all , hence we have
, hence we have 
Suppose that there exists a vertex  such that
such that , then
, then  and
and  satisfy
satisfy
(1), which contradicts the choice of , therefore
, therefore  for all
for all 
Now we define
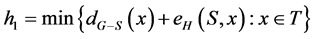 and let
and let  be a vertex such that
be a vertex such that
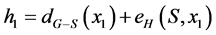 .
.
Note that 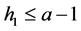 holds, we consider two cases.
holds, we consider two cases.
Cases 1: 
Note that ,
,  ,
, , and
, and .
.
By (1), we obtain

This is a contradiction.
Cases 2: 
It is clear that , then we defined
, then we defined  and let
and let
 be a vertex such that
be a vertex such that  by the condition of Theorem 2, the following inequality holds:
by the condition of Theorem 2, the following inequality holds:

which implies
 (2)
(2)
Note that the number of vertices in 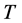 which satisfies the equality
which satisfies the equality  is at most
is at most , and the rest of vertices in
, and the rest of vertices in  satisfy
satisfy .
.
So we obtain

And further by (1)
 .
.
Note that  and
and , so we have
, so we have

and hence
 (3)
(3)
By (2) (3) we have
 (4)
(4)
Let 
Let , we have
, we have , Note that
, Note that , it is easy to see that
, it is easy to see that  is the minimum when
is the minimum when .
.
So we have
 (5)
(5)
If , by (5) we have
, by (5) we have 
This is a contradiction.
So we suppose , and hence
, and hence . By (5) we have
. By (5) we have

This is a final contradiction. Therefore theorem 2 is proved.