1. Introduction
The value distribution theory of meromorphic functions occupies one of the central places in Complex Analysis which now has been applied to complex dynanics, complex differential and functional equations, Diophantine equations and others.
In his excellent paper [1], W.K. Hayman studied the value distribution of certain meromorphic functions and their derivatives under various conditions. Among other important results, he proves that if f(z) is a transcendental meromorphic function in the plane, then either f(z) assumes every finite value infinitely often, or every derivative of f(z) assumes every finite nonzero value infinitely often. This result is known as Hayman’s alternative. Thereafter, the value distribution of derivatives of transcendental functions continued to be studied.
In this paper, we study the value distribution of transcendental meromorphic functions, all but finitely many of whose zeros have multiplicity at least , where
, where  is a positive integer.
is a positive integer.
In 2008, Liu et al. [2] proved the following results.
Theorem A Let  be an integer, let
be an integer, let  be a meromorphic function of infinite order
be a meromorphic function of infinite order 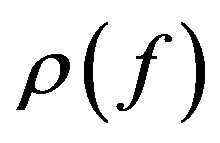 in
in , and let
, and let , where
, where 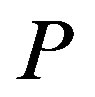 is a polynomial. Suppose that 1) all zeros of
is a polynomial. Suppose that 1) all zeros of 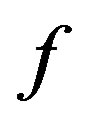 have multiplicity at least
have multiplicity at least , except possibly finitely many, and 2) all poles of
, except possibly finitely many, and 2) all poles of  are multiple, except possibly finitely many.
are multiple, except possibly finitely many.
Then 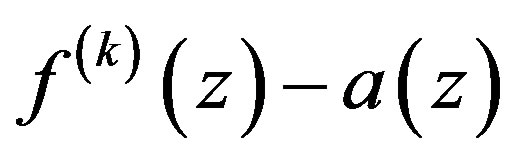 has infinitely many zeros.
has infinitely many zeros.
Theorem B Let 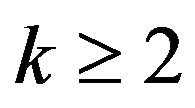 be an integer, let
be an integer, let  be a meromorphic function of finite order
be a meromorphic function of finite order 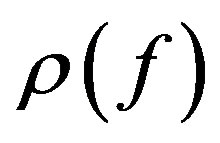 in
in , and let
, and let , where
, where 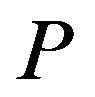 is a polynomial. Suppose that 1) all zeros of
is a polynomial. Suppose that 1) all zeros of  have multiplicity at least
have multiplicity at least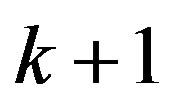 , except possibly finitely many, and 2)
, except possibly finitely many, and 2) .
.
Then 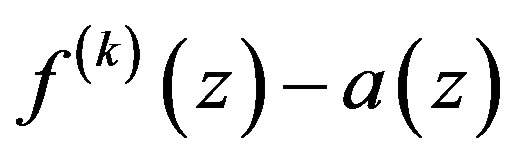 has infinitely many zeros.
has infinitely many zeros.
In the present paper, we prove the following result, which is a significant improvement of Theorem 1.
Theorem 1 Let  be an integer, let
be an integer, let  be a meromorphic function of order
be a meromorphic function of order  in
in , and let
, and let , where
, where  is a polynomial. Suppose that all zeros of
is a polynomial. Suppose that all zeros of 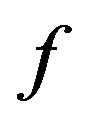 have multiplicity at least
have multiplicity at least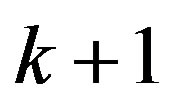 , except possibly finitely many. Then
, except possibly finitely many. Then 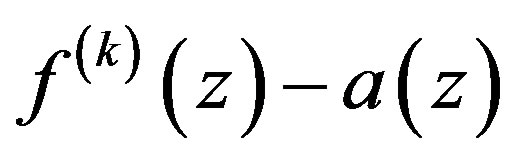 has infinitely many zeros.
has infinitely many zeros.
Theorem 1 and Theorem 2 taken together imply the following result.
Theorem 2 Let 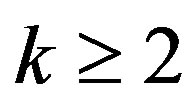 be an integer, let
be an integer, let  be a meromorphic function in
be a meromorphic function in , and let
, and let , where
, where 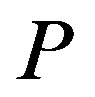 is a polynomial. Suppose that 1) all zeros of
is a polynomial. Suppose that 1) all zeros of  have multiplicity at least
have multiplicity at least , except possibly finitely many, and 2)
, except possibly finitely many, and 2) 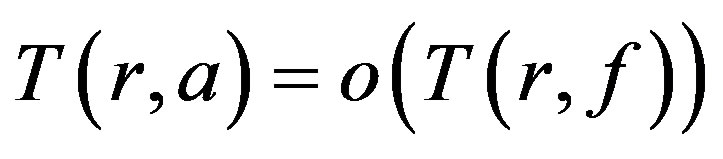 as
as .
.
Then 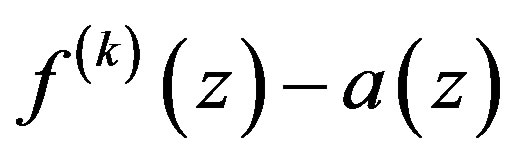 has infinitely many zeros.
has infinitely many zeros.
2. Notation and Some Lemmas
We use the following notation. Let  be complex plane and
be complex plane and  be a domain in
be a domain in . For
. For  and
and ,
,  and
and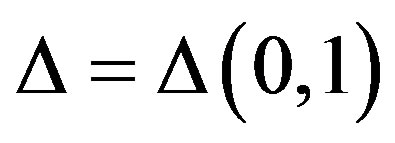 . We write
. We write 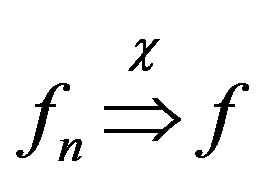 in
in  to indicate that the sequence
to indicate that the sequence 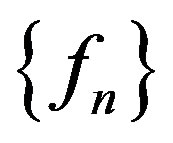 converges to
converges to 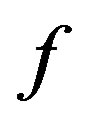 in the spherical metric uniformly on compact subsets of
in the spherical metric uniformly on compact subsets of  and
and 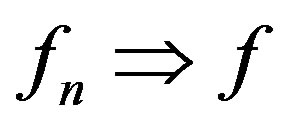 in
in  if the convergence is in the Euclidean metric.
if the convergence is in the Euclidean metric.
Let 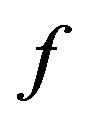 be a meromorphic function in
be a meromorphic function in . Set
. Set
 (1.1)
(1.1)
The Ahlfors-Shimizu characteristic is defined by
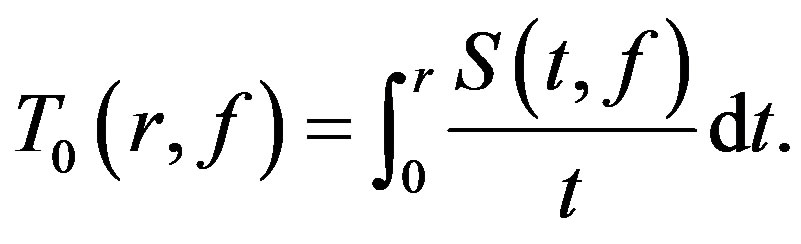
Remark Let 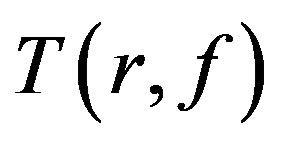 denote the usual Nevanlinna characteristic function. Since
denote the usual Nevanlinna characteristic function. Since 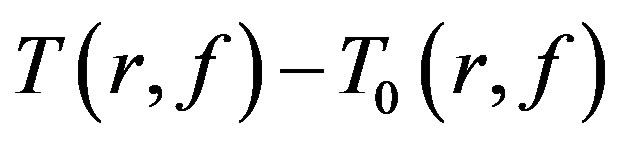 is bounded as a function of
is bounded as a function of , we can replace
, we can replace  with
with  in the paper.
in the paper.
The order 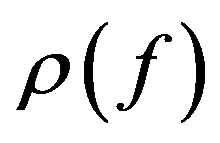 of the meromorphic function
of the meromorphic function  is defined as
is defined as

Lemma 1 [3] Let  a sequence of holomorphic functions in
a sequence of holomorphic functions in  such that
such that 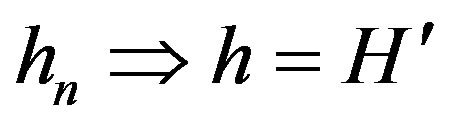 locally uniformly in
locally uniformly in , where
, where  is univalent in
is univalent in . Let
. Let 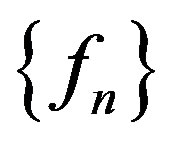 be a sequence of functions meromorphic in
be a sequence of functions meromorphic in  such that for each
such that for each 1) all zeros of
1) all zeros of 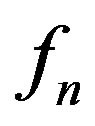 have multiplicity at least
have multiplicity at least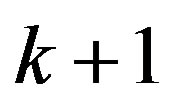 ; and 2)
; and 2) .
.
Then  is quasinormal of order 1 in
is quasinormal of order 1 in . If, moreover, no subsequence of
. If, moreover, no subsequence of  is normal at
is normal at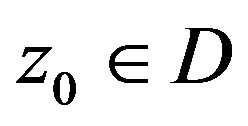 , then
, then
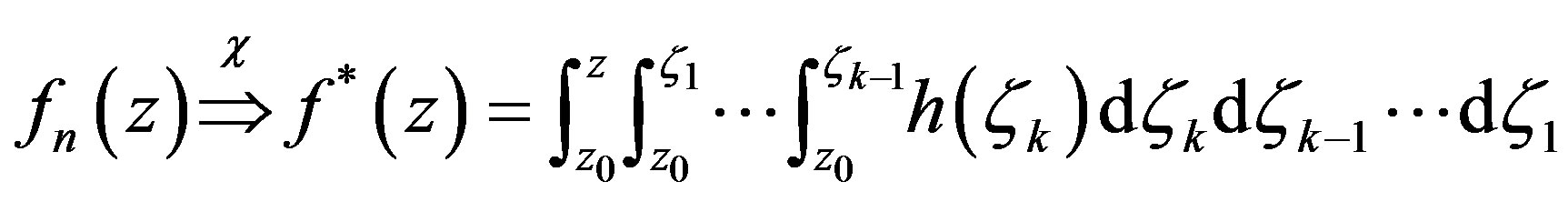
locally uniformly in  and there exists
and there exists  such that
such that  for all
for all .
.
Remark Since Lemma 1 is not stated explicitly in [3], let us indicate how it follows from the results of that paper. The proof that  is quasinormal of order 1 is essentially identical to that of Theorem
is quasinormal of order 1 is essentially identical to that of Theorem  of [3]. That proof also shows that condition (b) of Lemma 7 in [3] holds for
of [3]. That proof also shows that condition (b) of Lemma 7 in [3] holds for . It then follows from Lemma 7 that
. It then follows from Lemma 7 that  locally uniformly on
locally uniformly on . The bound on
. The bound on 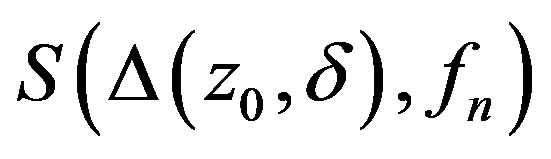 follows from Lemma 9 of [3]. See also [4, Remark on page 484].
follows from Lemma 9 of [3]. See also [4, Remark on page 484].
Lemma 2 [5, Lemma 2] Let 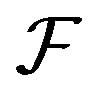 be a family of functions meromorphic in
be a family of functions meromorphic in , all of whose zeros have multiplicity at least
, all of whose zeros have multiplicity at least , and suppose that there exists
, and suppose that there exists  such that
such that 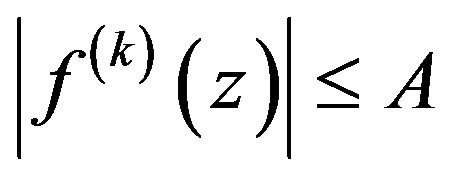 whenever
whenever . Then if
. Then if  is not normal at
is not normal at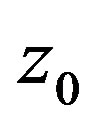 , there exist, for each
, there exist, for each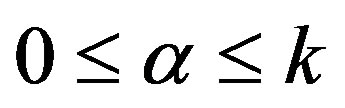 1) points
1) points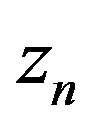 ,
, ;
;
2) functions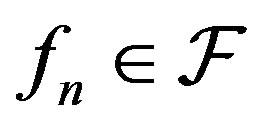 ; and 3) positive numbers
; and 3) positive numbers 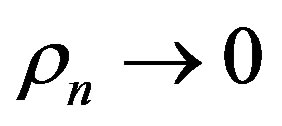
such that 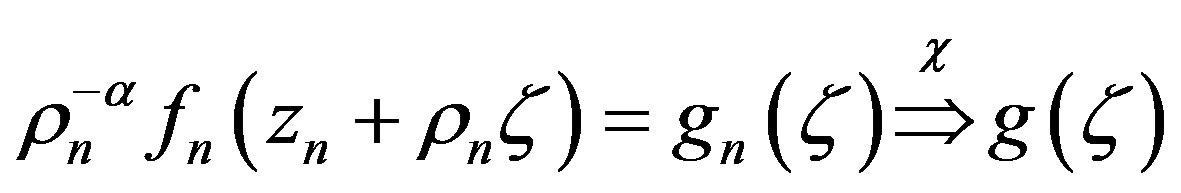 in
in , where
, where 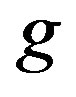 is a nonconstant meromorphic function in
is a nonconstant meromorphic function in all of whose zeros have multiplicity at least
all of whose zeros have multiplicity at least , such that
, such that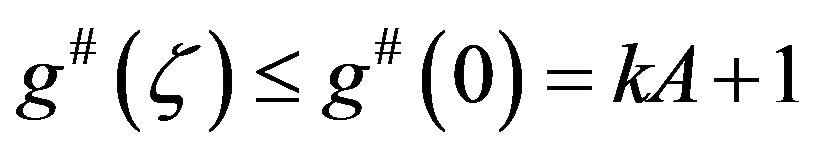 .
.
Lemma 3 Let 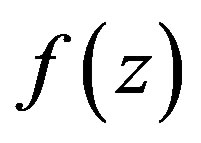 be a meromorphic function of order
be a meromorphic function of order  in
in , then there exist
, then there exist  and
and  such that
such that
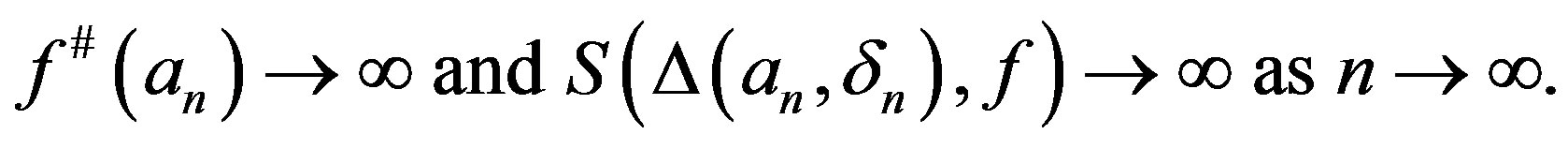
Proof We claim that there exist 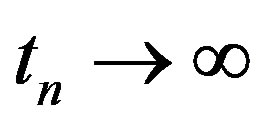 and
and 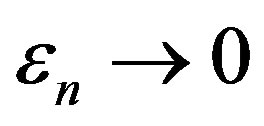 such that
such that
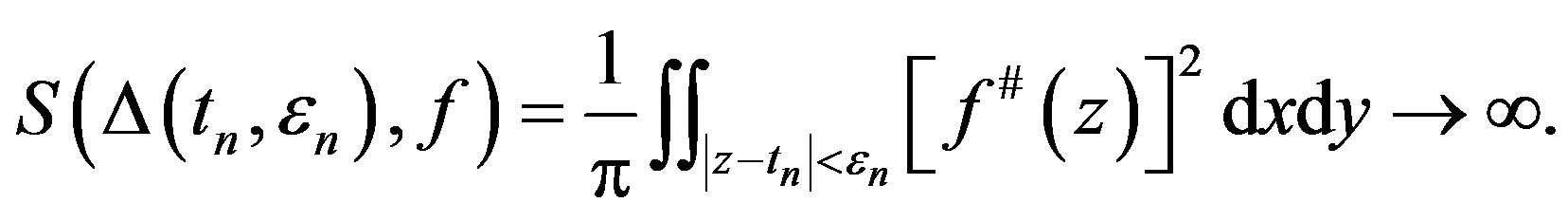 (1.2)
(1.2)
Otherwise there would exist  and
and 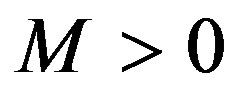 such that
such that
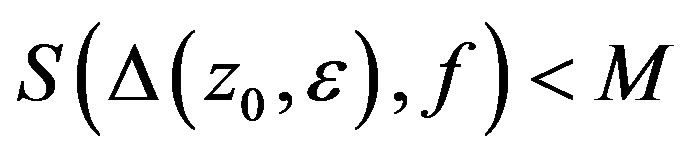
for all . From this follows
. From this follows

and hence

Now we have  which contradicts the hypothesis that
which contradicts the hypothesis that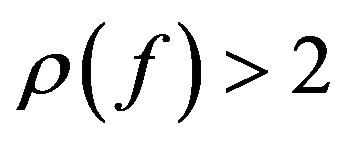 .
.
Observing that  hence there exists a sequence
hence there exists a sequence 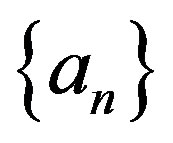 such that
such that 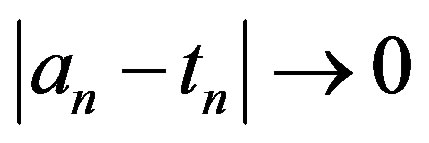 and
and  as
as . Let
. Let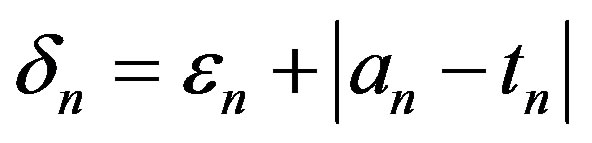 . Obviously,
. Obviously,  and
and  , and hence
, and hence  as
as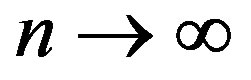 .
.
Lemma 4 Let  and
and . Let
. Let 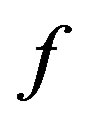 be a transcendental meromorphic function, all of whose zeros have multiplicity at least
be a transcendental meromorphic function, all of whose zeros have multiplicity at least . Set
. Set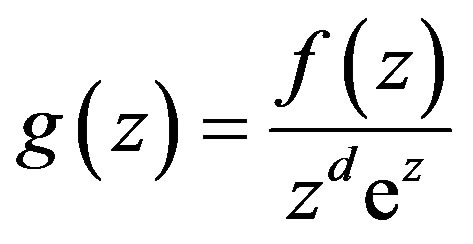 . Suppose that
. Suppose that . Then there exists a sequence
. Then there exists a sequence
 and
and  such that
such that
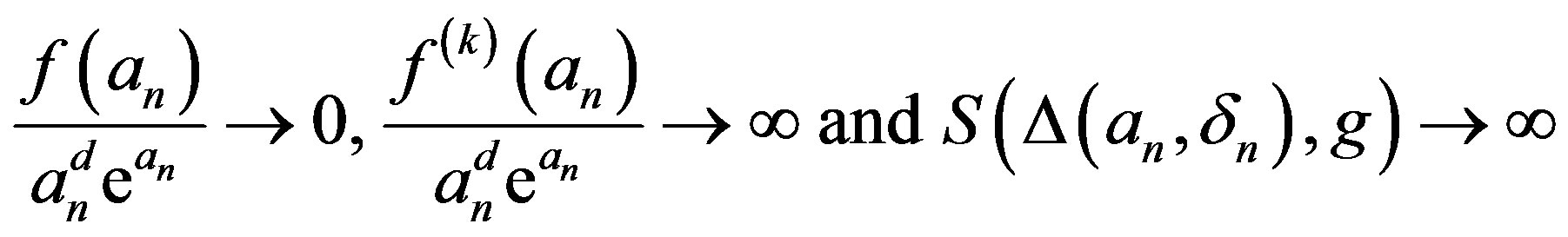
as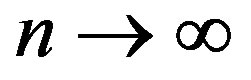 .
.
Proof Since  and
and , we have
, we have . By Lemma 3, there exist
. By Lemma 3, there exist  and
and 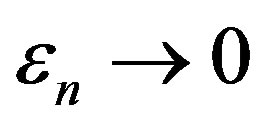 such that
such that
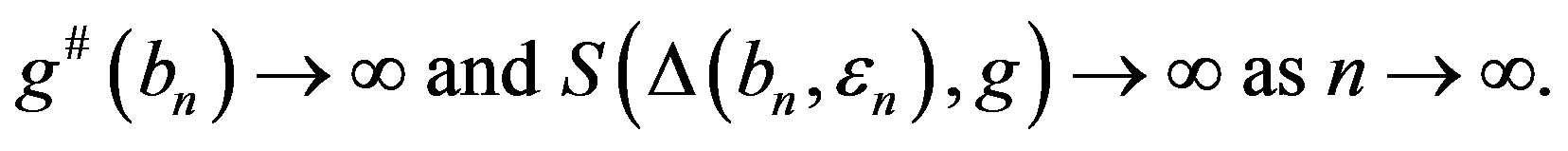
Set . Clearly,
. Clearly,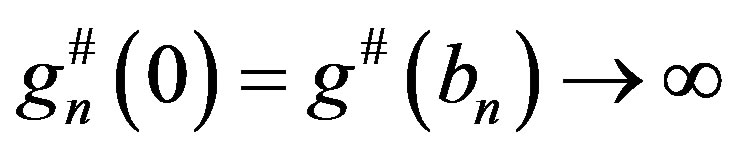 . Thus
. Thus 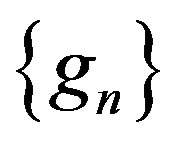 is not normal at 0. Obviously, all zeros of
is not normal at 0. Obviously, all zeros of  have multiplicity at least
have multiplicity at least  in
in , and hence all zeros of
, and hence all zeros of 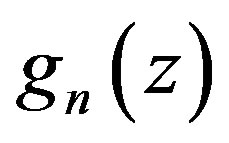 have multiplicity at least
have multiplicity at least 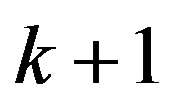 in
in  for sufficiently large
for sufficiently large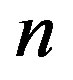 . Using Lemma 2 for
. Using Lemma 2 for , there exist points
, there exist points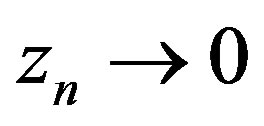 , and positive numbers
, and positive numbers  and a subsequence of
and a subsequence of 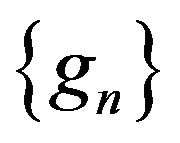 (that we continue to call
(that we continue to call ) such that
) such that
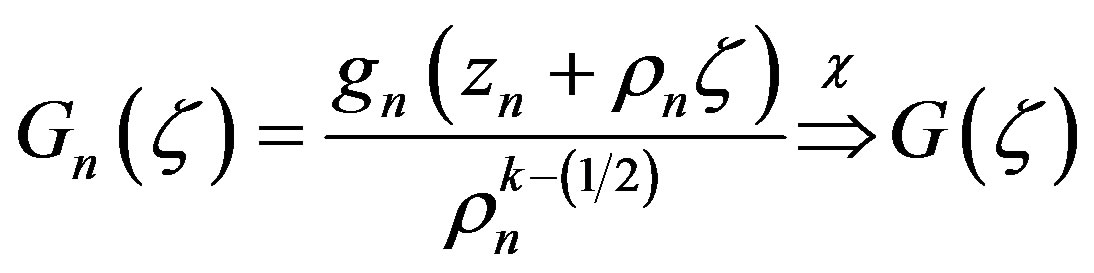
in , where
, where  is a nonconstant meromorphic function in
is a nonconstant meromorphic function in , all of whose zeros have multiplicity at least
, all of whose zeros have multiplicity at least .
.
We claim that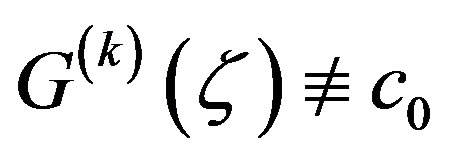 , where
, where 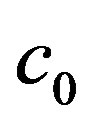 is a constant. Otherwise,
is a constant. Otherwise, 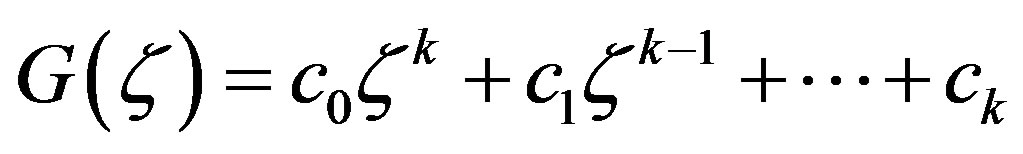 , where
, where 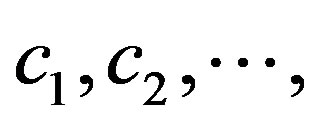 and
and 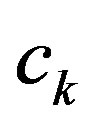 are constants. Then, either
are constants. Then, either  is a constant function, or all zeros of
is a constant function, or all zeros of 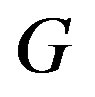 have multiplicity at most
have multiplicity at most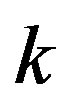 . A contradiction.
. A contradiction.
Let  be not a zero or pole of
be not a zero or pole of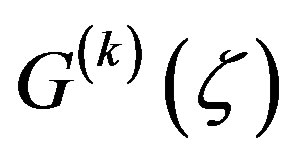 , and let
, and let . Now we have
. Now we have
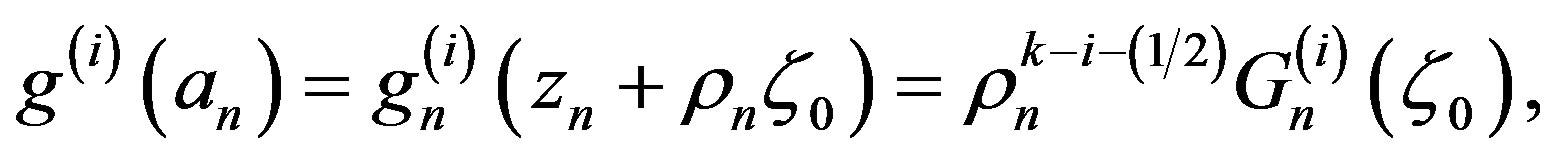
where . Since
. Since 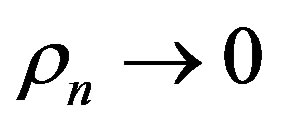 and
and 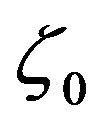 is not a zero or pole of
is not a zero or pole of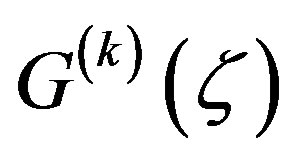 , we have
, we have ,
, 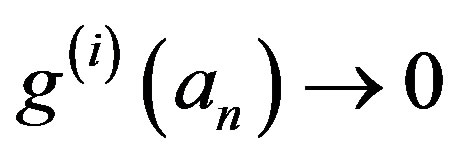 and
and  as
as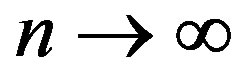 , where
, where .
.
Set 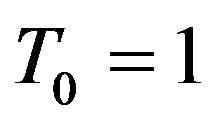 and
and , where
, where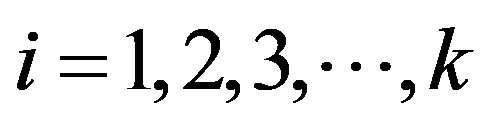 . Clearly,
. Clearly,
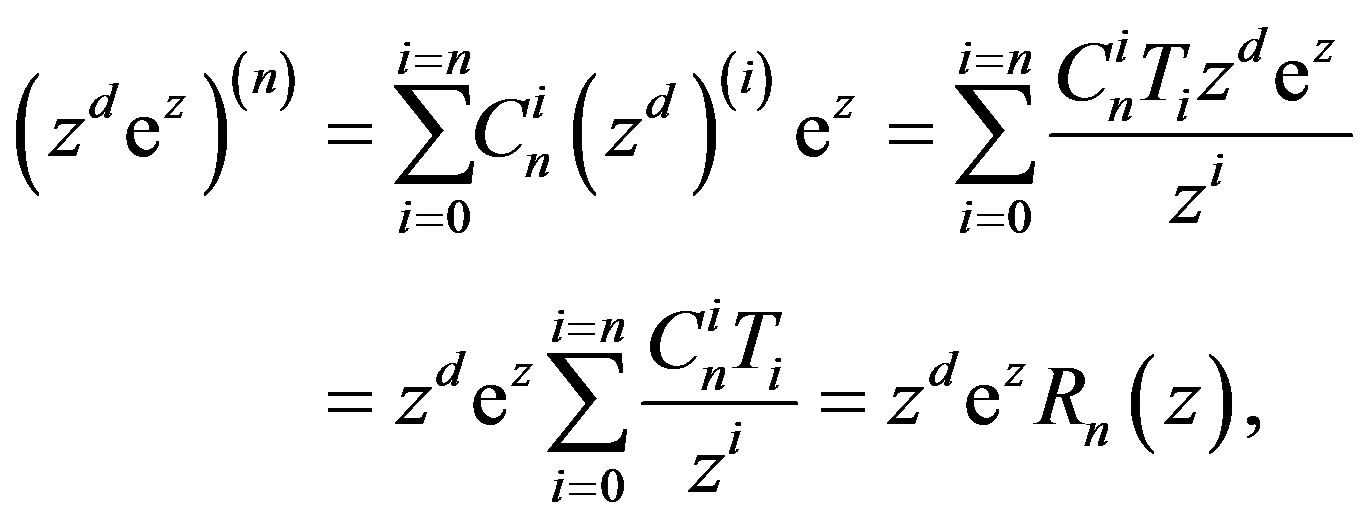
where  satisfying
satisfying 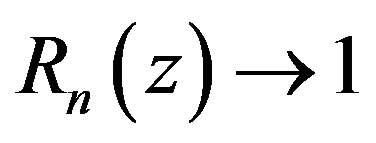 as
as .
.
Now, we have 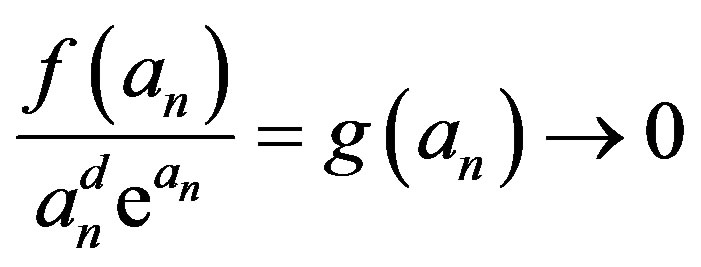 and
and

Set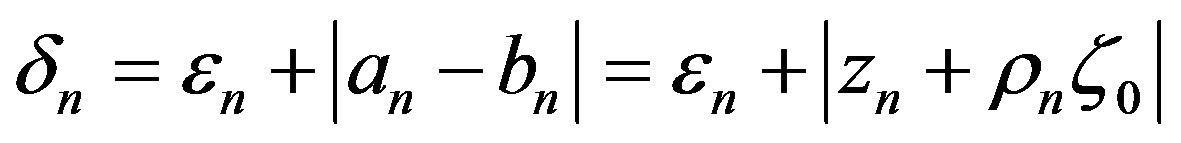 . Obviously,
. Obviously,  and
and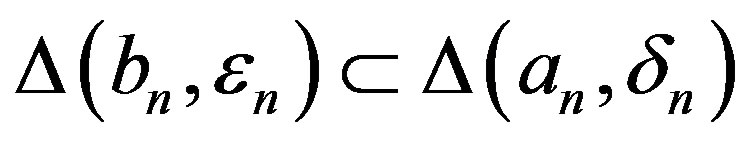 , and hence
, and hence 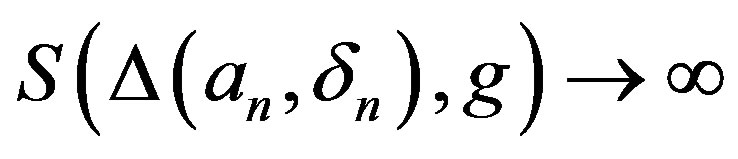 as
as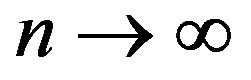 .
.
3. Proof of Theorem
Proof We assume that 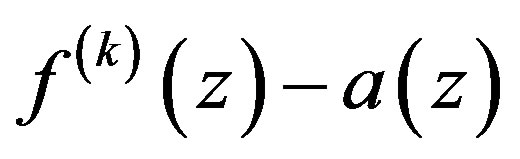 has at most finitely many zeros and derive a contradiction. Let
has at most finitely many zeros and derive a contradiction. Let 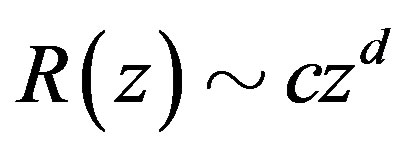 as
as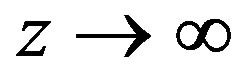 , where
, where 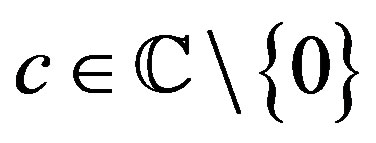 and
and .
.
Set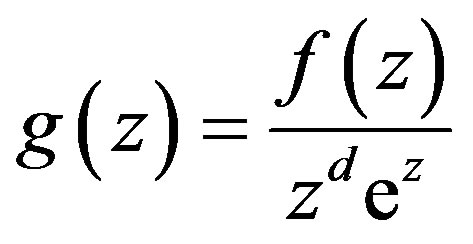 . By Lemma 4, there exists a sequence
. By Lemma 4, there exists a sequence  and
and  such that
such that
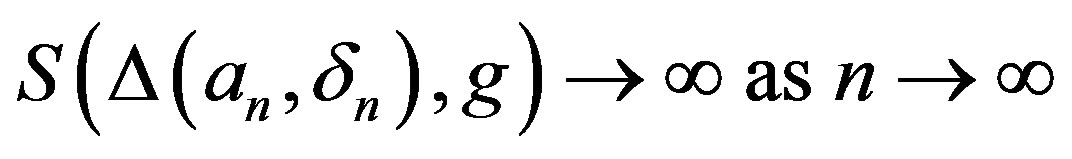 (1.3)
(1.3)
and
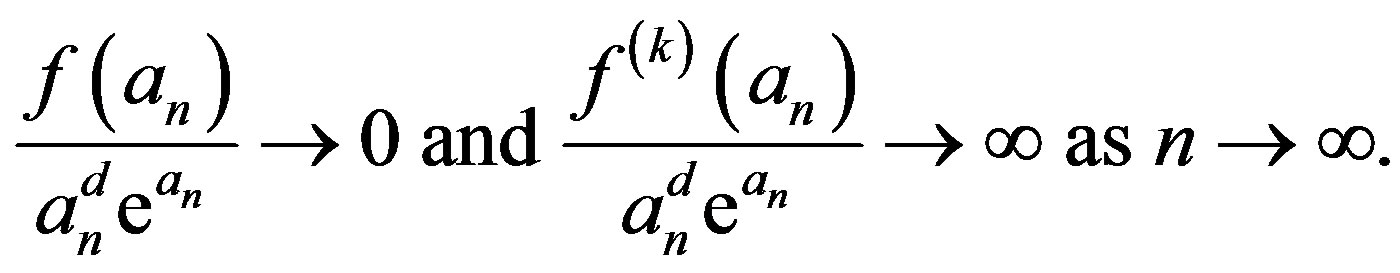 (1.4)
(1.4)
Set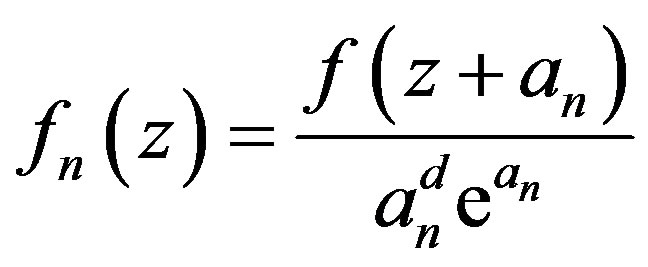 . By (1.4),
. By (1.4),
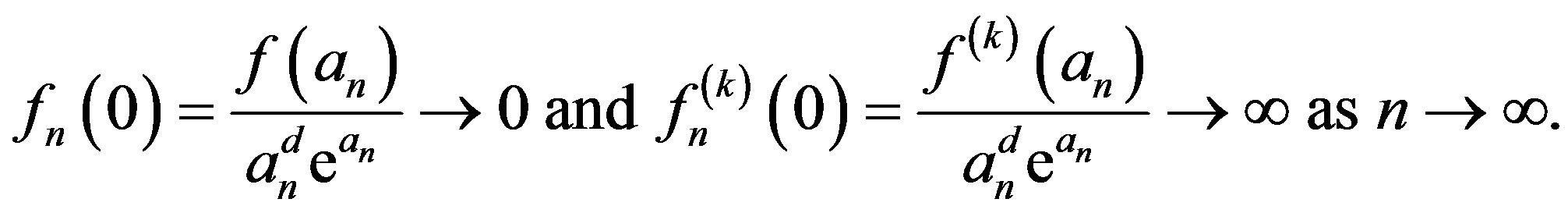 (1.5)
(1.5)
Hence, no subsequence of 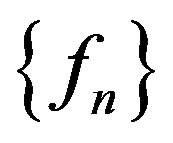 is normal at
is normal at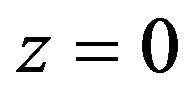 .
.
Since  has at most finitely many zeros, we have for sufficiently large
has at most finitely many zeros, we have for sufficiently large ,
,
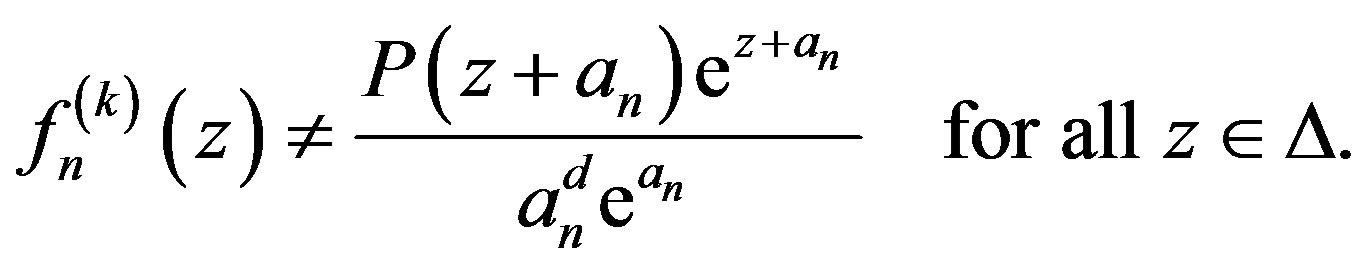
Observing that
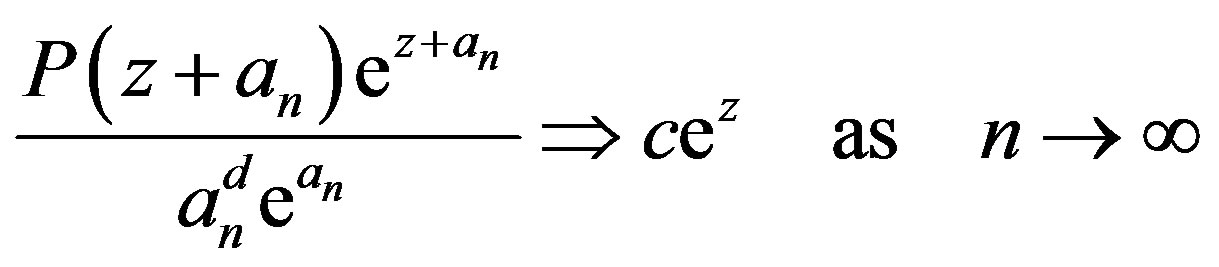
in . It follows from Lemma 1 (applied to
. It follows from Lemma 1 (applied to  in
in ), and there exists
), and there exists  such that for all
such that for all 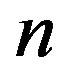
 (1.6)
(1.6)
Set . Then
. Then
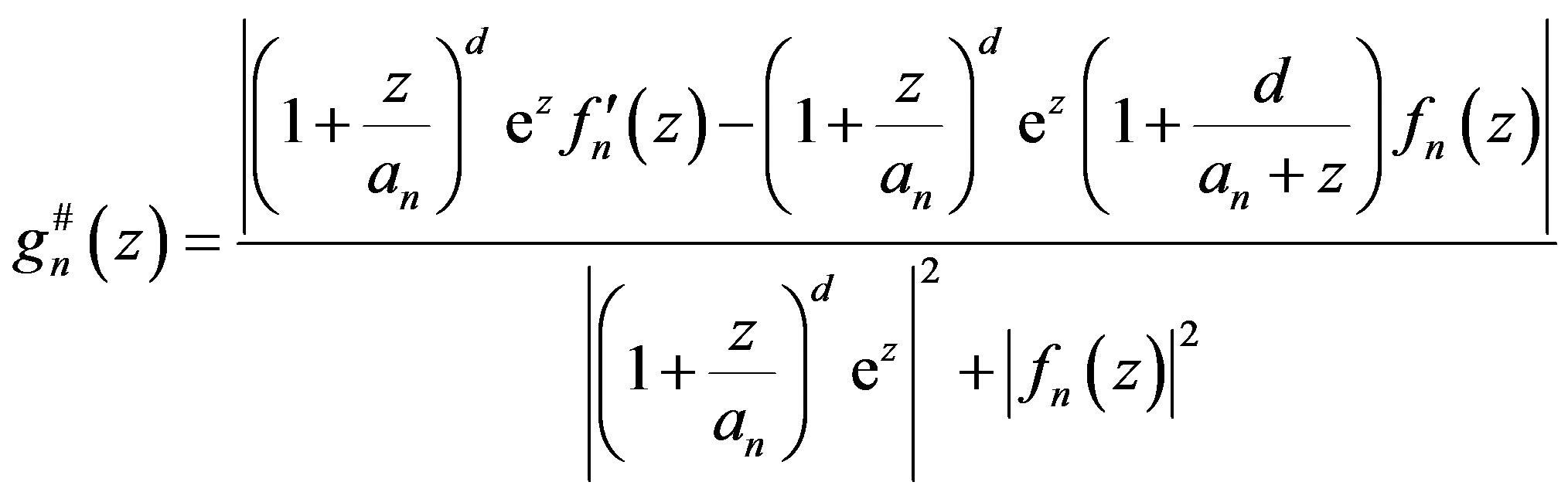
and hence
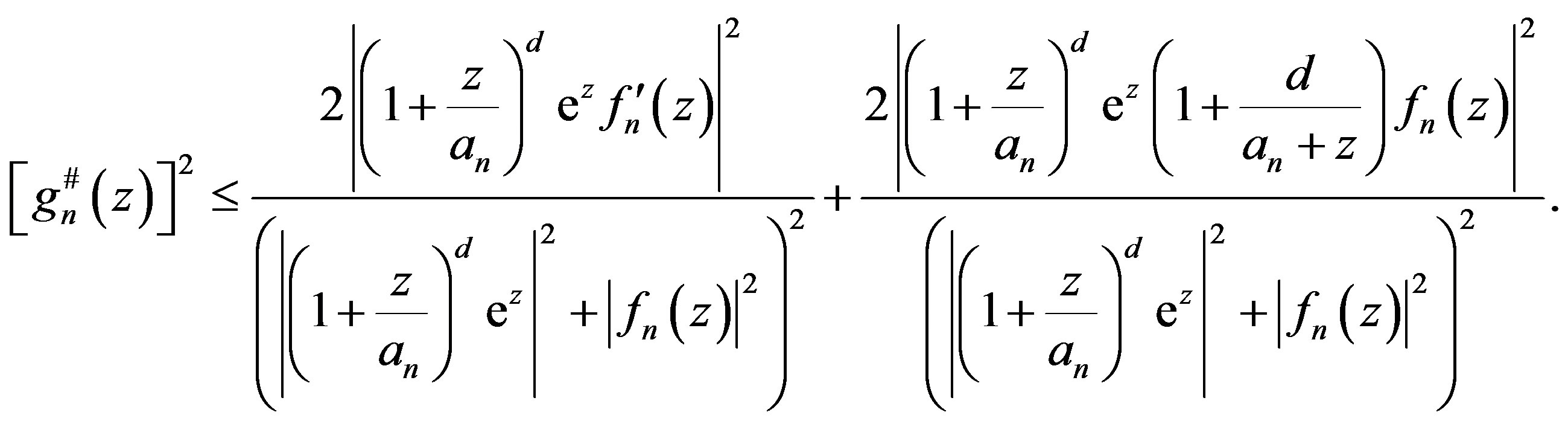 (1.7)
(1.7)
Using the simple inequality
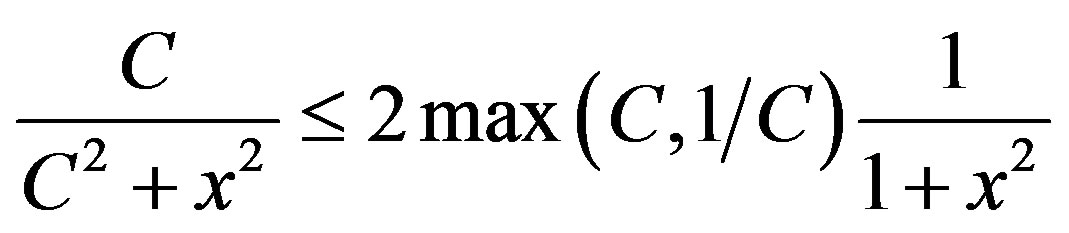
for , we have
, we have
 (1.8)
(1.8)
The second term on the right of (1.7) is
 (1.9)
(1.9)
Putting (1.7), (1.8), and (1.9) together, we have for 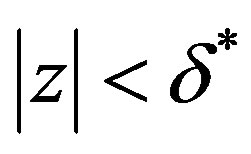 and sufficiently large
and sufficiently large ,
,
 (1.10)
(1.10)
It follows from (1.1), (1.6), and (1.10),
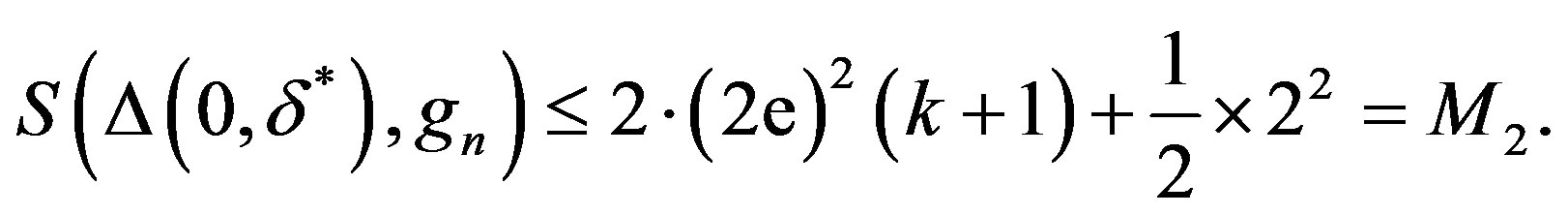
Thus,

which contradicts (1.3).
Acknowledgements
This work was supported by National Natural Science Foundation of China (No.11001081, No.11226095).
[1] W. K. Hayman, “Picard Values of Meromorphic Functions and Their Derivatives,” Annals of Mathematics, Vol. 70, No. 1, 1959, pp. 9-42. http://dx.doi.org/10.2307/1969890
[2] X. J. Liu, S. Nevo and X. C. Pang, “On the kth Derivative of Meromorphic Functions with Zeros of Multiplicity at Least k+1,” Journal of Mathematical Analysis and Applications, Vol. 348, No. 1, 2008, pp. 516-529. http://dx.doi.org/10.1016/j.jmaa.2008.07.019
[3] S. Nevo, X. C. Pang and L. Zalcman, “Quasinormality and meromorphic functions with multiple zeros,” Journal d’Analyse Math??matique, Vol. 101, No. 1, 2007, pp. 1-23.
[4] X. C. Pang, S. Nevo and L. Zalcman, “Derivatives of Meromorphic Functions with Multiple Zeros and Rational Functions,” Computational Methods and Function Theory, Vol. 8, No. 2, 2008, pp. 483-491. http://dx.doi.org/10.1007/BF03321700
[5] X. C. Pang and L. Zalcman, “Normal Families and Shared Values,” Bulletin London Mathematical Society, Vol. 32, No. 3, 2000, pp. 325-331. http://dx.doi.org/10.1112/S002460939900644X