On the Influence of Particles Characteristics on Moisture Diffusivity during Drying of Granular Porous Media ()
Keywords:Adsorption; Desorption; Diffusion; Fick; Knudsen; Mass Transfer
1. Introduction
The use of dry air from adsorption processes is a very frequent activity in numerous industrial operations. Especially for drying processes, this may be a very interesting practice, since the operational conditions of the air influence the drying kinetics significantly [1]. An appropriate use of these conditions favors the reduction of the total process time and operational costs, promotes an increase in drying capacity, and provides a better control of the operational variables of entry and a final product of better characteristics. The water vapor contained in the moist ambient air is usually removed when air percolates the adsorption columns which are coupled to the fluid feeding system of the dryer. The columns are made up of particles of desiccant inorganic compounds with high porosity and surface area. Air humidity is then removed by means of physical attraction of water molecules to the adsorbent surface of particles and a balance between water and air is established. When the available pores are filled with water, moisture is removed by capillary condensation when the pressure of the saturated vapor is reduced due to surface tension effects [1]. Once partially saturated with moisture, the adsorption columns must be thermally regenerated upon drying so that they can be used again in the desorption process of moist air.
The drying of an adsorption column can be performed by subjecting it to an upward single-phase flow of heated air. Under this condition, air percolates the interconnected voids of the column; however, the voids that do not share a connection impose resistance to the fluid flow and cause changes in its trajectory and a continuous variation of permeability throughout the adsorptive column, which characterizes the system as a porous medium. In the drying of three-phase porous media (air, water and solid), moisture may diffuse in the form of liquid and vapor in the final stages of the process, where different diffusive mechanisms, mainly, may be present and influence the way that moisture is removed from the porous medium. It is known that drying kinetics of a single particle is dependent on its diameter and other characteristics [2], and it also involves not only diffusive mechanisms, but also a complex interaction between diffusive and capillary phenomena. The adequate knowledge of the mass transfer phenomenon and, above all, the identification of the predominant drying mechanism are especially important for the drying of porous media. The objective of this work is included in this context. The drying of porous media consisting of different diameters of activated alumina particles was experimentally studied by obtaining moisture data as a function of time for a specific operational condition. From the experimental results obtained, the main mechanisms of moisture transfer present in drying were determined and, finally, the predominant mass transfer mechanism was identified.
2. Drying Kinetics
The drying experiments were performed with three different porous media, which were of cylindrical geometry, unconsolidated and with dimensions of 1 cm in height and 10 cm in diameter. The difference between the media lies in the fact that each was artificially prepared with activated alumina particles (F-200 type, Alcoa), which were moist and had particular dimensions with the purpose of giving the porous media different physical properties and distinct characteristics regarding heat and mass transfer. According to the XRD diffractograms for each particle diameter used (Figure 1), the activated alumina particles are inorganic compounds formed by Bayerite (Al2O3·3H2O) and Bohemite (AlO (OH)), mainly. The X-ray diffraction patterns were obtained by the powder method on a Rigaku (Multiflex) diffractometer with Cu tube and Ni filter. The experiments were performed with CuKα radiation (λ = 0.1542 nm). The speed of the goniometer was used at 2˚ 2θ·min−1, step 0.02˚ and a varying angle in the range from 5˚ to 80˚ (2θ). It is possible to note in Figure 1 that the patterns at 2θ of 20˚ and 40˚ of the three curves are different. Considering that the diffraction pattern of a crystalline material is a function of its crystal structure, this fact can be attributed to the granulation process of the alumina powder, once the material came from the same batch. If temperature is required to stabilize the alumina pellets in an industrial process, this can promote better crystallization.
The alumina particles were subjected to a water column of 80 cm of height for a period of 24 h to ensure the maximum moisture saturation possible of the porous medium at the beginning of the drying process. Water, under pressure, percolates the available pores of the particle expelling the air contained in the interstices. The porous media were subjected to an upward single-phase flow of heated air and their mass was measured at pre-established time intervals with a semi-analytical scale. This procedure was repeated until significant mass variation was no longer found. The dry mass was obtained by keeping the particles, which made up the medium, in an oven with air circulation at 105˚C ± 3˚C for 24 hours.
Figure 2 shows the moisture data as a function of time for the porous media consisting of different particle diameters. Drying was performed at the temperature of 40˚C and with maximum velocity of the air current used in the experiments (3.5 m/s). This condition was applied in order for the mass transfer coefficient between the air and the surface of the porous medium to be sufficiently large so that only the diffusive mechanisms would be analyzed, without compromising the results. Nevertheless, with the obtaining of the drying rate as a function of moisture content of the medium, it was proven that the period of constant rate still existed, even if for a short period of time. Therefore, Figure 2 shows the data of moisture as a function of time for t > 4 min, when the period of decreasing drying rate starts. At t = 5 min, moisture corresponds to the critical moisture content.

Figure 1. XRD diffractograms of alumina particles.

Figure 2. Drying kinetics of porous media consisting of different particle diameters.
It can be verified from the data presented in Figure 2 that, for the same operational condition employed, the drying kinetics of porous media of equivalent geometry is different and is dependent on the particle diameter used in the preparation of the porous media. It is clear that each porous medium studied imposes resistance to moisture transfer from their interstices to their surface. It is intuitive to think, in a first analysis, that there is a difference among curves of drying kinetics for the porous media consisting of different alumina particle diameters. Resistance to moisture diffusivity is greater for particles of larger diameters. Thus, the vapor flow on the surface of the particle is lower, once flow becomes independent of the surface area during the drying stage in which diffusive mechanisms limit the process. It is worth highlighting that this area has low moisture concentration due to the resistance imposed to moisture diffusion (liquid and vapor) by the structure of the material during the period at falling drying rate. The motivation to investigate the results shown in Figure 3, however, is to establish the mechanism which caused the influence on the drying curves. This information is also important when performing simulation of the experimental data mainly with pseudo-homogeneous models. A characterization of the particulate matter was performed in order to obtain information on those issues and the results were used to obtain mass parameters.
3. Characterization of Particulate System
Since the particles that constitute the porous media significantly influence their drying kinetics, it is important to obtain qualitative and quantitative information on the physical characteristics of the particles. The objective is to understand the reason for the existence of such influence in the data presented in Figure 2. Thus, the alumina particles were characterized according to their dimensions, morphology, sphericity, specific mass, porosity and pore size distribution. Preliminarily, Figure 3 shows the nitrogen adsorption and desorption isotherms.
The isotherms were acquired using the BET method. The presence of hysteresis can be observed in the dimensionless pressure range between 0.5 and 0.95, which suggests that the quantity of N2 to be desorbed is greater in this range. According to Keey [3], this is related to capillary condensation in mesopores. The way the particle adsorbs and desorbs nitrogen, as shown in Figure 3, is characteristic of mesoporous and macroporous solids. Therefore, alumina particles may have two families of pores, one with pore diameter from 2 to 50 nm, and another with pore diameter greater than 50 nm [3]. Thus, pore size distribution is necessary to identify the predominant pore size of particles, since it is an important property for the study of the porous structure and to identify the mass transfer mechanism, once it is closely related to the total area of the solid matrix. As an example, Figure 4 shows the pore size distribution of the particle of 4 mm in diameter from nitrogen adsorption studies.
It can be observed from the data in Figure 4 that the macropore family is non-existent, since distribution is between the pores of 1.89 and 44.18 nm. This result was

Figure 3. N2 sorption isotherms for particle diameter of 2.80 mm.

Figure 4. Pore size distribution for particle diameter of 4 mm.
also verified for the other types of particle diameter studied. On the basis of the distribution curve, a greater quantity of pores with diameters between 2.6 and 5 nm can be verified, followed by an intermediate quantity with diameters between 15 to 25 nm. Some pores present in the alumina particles in lower quantities, however, have diameters larger than 25 nm and a little portion of pores have diameters smaller than 2 nm, belonging to the micropore class, Keey [3]. Figure 5 shows an image of the surface of the alumina particle (3.35 mm in diameter) enlarged 10,000 times. In the image obtained by Scanning Electron Microscopy (SEM), it can be observed that the surface is rough and that there is presence of pores, which correspond to the darker points in the image. SEM was performed in a microscopic FEI Inspect S 50.
Table 1 contains the values of average diameter and pore volume for each particle diameter studied, as well as surface area values. It is possible to see that particles have a large surface area and that most of the existing pores belong to the mesopore family. Alumina particles were also characterized according to their shape and dimensions. Table 2 shows the main properties obtained

Figure 5. SEM of the alumina particle diameter of 3.35 mm.

Table 1. Structural characterization of the alumina particles.

Table 2. Characterization of the size and shape of the alumina particles.
with the aid of the Image Pro Plus® software. Images obtained with a microscope were previously scanned and acquired by an image acquiring system. From the data presented, it is possible to highlight the high sphericity of particles (ϕ > 90%) and the increase in area, perimeter and Feret diameter, as particle diameter, as expected. Table 3 shows the data for specific mass and porosity. Apparent specific mass was obtained using a liquid pycnometer and hexane as solvent, and a gas pycnometer and helium were used to obtain the real specific mass of the particle. Porosity was acquired from the specific mass

Table 3 . Physical properties of the alumina particles.
data. It can be seen that particle porosity is high and reinforces the hysteresis effect on the sorption isotherm. From the characterization data presented, it can be verified that each particle diameter presents distinct physical properties, which probably influenced the diffusive and mass transfer mechanisms and, consequently, the drying kinetics curves presented in Figure 2. Nonetheless, in order to better discuss the results presented, it is necessary to identify the relationship between particle characteristics and the diffusive phenomena.
4. Diffusivity Estimation
The literature generally treats ordinary liquid diffusion as the predominant mechanism in the drying of porous media. However, liquid evaporation may also occur in the interstices of the solid matrix, causing the vapor concentration gradients to be established during moisture diffusion. According to Keey [3], evaporation plays an important role in the drying process and moisture can migrate from inside the solid to its surface both in the vapor phase and in the liquid phase and mechanisms may include diffusion in each phase. According to Chen [4], only liquid diffusion is not enough to accurately describe the drying process, once, at a certain stage of the process, a vapor concentration profile can be established through the porous medium. Considering a one-dimensional Cartesian coordinate system, and an isothermal process, the partial differential equations which take into account spatial distribution of moisture content (vapor and liquid) in transient regime are:
 (1)
(1)
 (2)
(2)
Traditionally, both phenomena (liquid and vapor diffusion) are encompassed into a single parameter, effective diffusivity, to account for the influence of vapor diffusion on moisture transfer. Chen [4] states that this parameter is a complex interaction between the variables involved in the drying process, such as temperature, moisture and pressure. Once it is imposed that vapor and liquid diffusion are the predominant phenomenon in drying at falling rate, different diffusive mechanisms can be present in the drying of alumina porous media, both associated with the respective transport of liquid or vapor. The diffusion mechanisms that can be present in the liquid transport are ordinary liquid diffusion and superficial diffusion. When it comes to moisture transport in the vapor phase, diffusion and effusion (Knudsen diffusion) can establish during the period of drying at decreasing rate.
Initially, it is possible to identify at which stage moisture is spread in the interstices of the porous medium from data of particle distribution in the pores. According to Kelvin’s Law [3], the effect of particle pore size on water activity can be considered negligible for pores with diameter larger than 10 nm. From the nature of the pore distribution obtained (Figure 4), it can be verified that capillarity is possibly one of the mechanisms that control internal transfer of moisture, since the alumina particle presents pores with diameter smaller than 10 nm and an average pore size of 5.95 nm (Table 1). Once capillary effects have influence on moisture transfer, ordinary liquid diffusion is fundamentally associated with these effects. The movement of liquid within the solid matrix occurs due to the difference in relative attraction between liquid molecules and liquid-solid molecules. Mathematically, the capillary phenomenon is modeled for a Cartesian coordinate system and one-dimensional problem according to the equation:
 (3)
(3)
A relationship between moisture permeability (Ks) and liquid diffusion can be made, according to Keey [3]:
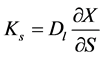 (4)
(4)
Hence, ordinary liquid diffusion is associated with the capillary effects which control liquid diffusion from the interstices of the porous medium to its surface, where a vapor flow is established. Then, liquid diffusion is treated as an effective parameter because the characteristics of the porous solid influence the solid-liquid interactions, and it is estimated from the Arrhenius equation:
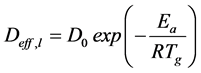 (5)
(5)
Besides ordinary liquid diffusion, another mechanism that may control moisture diffusion in the liquid phase is superficial diffusivity. This mechanism, as well as ordinary diffusivity, occurs due to concentration gradient of liquid and is also estimated with the Arrhenius Equation [5].
Ordinary vapor diffusion, on the other hand, is estimated with Equation (6), the most common equation used to treat moisture transfer in porous media [4]. Vapor diffusion is also treated as an effective parameter once the vapor faces various pore sizes when it spreads through the solid matrix. Tortuosity τ is a parameter of difficult experimental determination. Nonetheless, it can be estimated based on the capillary model theory [6]. For the alumina particles used, the average tortuosity value calculated was of 2.25, which is within the ideal range of values (2 - 20) for this parameter, as suggested by McCabe, Smith and Harriott [7]. The value of the constricivity factor was equal to the unit.
 (6)
(6)
The diffusion of water vapor in the drying air (Dv,0) can be known by means of analytical expressions available in the literature. Among a series of equations tested, the one that provides a value consistent with the literature is that proposed by Putrano and Chen [8]:
 (7)
(7)
When the particle pore size is smaller than the mean free path of the water vapor molecules, Knudsen diffusion occurs during the drying process. According to Baini and Langrish [9], effusion occurs for materials with pore diameter between 2 and 50 nm, which covers most of the pore diameters found. Knudsen diffusion, also treated as an effective parameter, is a function of the physical characteristics of particles, that is:
 (8)
(8)
It is, therefore, appropriate to define a new effective parameter that encompasses all diffusive mechanisms presented. Thus, the parameter to be estimated for the drying of porous media is the overall effective diffusivity, which is obtained from the harmonic mean of all diffusive mechanisms:
 (9)
(9)
The diffusive model is then mathematically described according to the Equation:
 (10)
(10)
Equation (10) is subjected to the following initial condition (for t = 0 and 0 ≤ z ≤ L):
 (11)
(11)
A boundary condition traditionally applied is the one that considers the bottom surface of the medium to be impermeable and moisture flow to be continuous in this region, that is (t > 0):
 (12)
(12)
Assuming that the top surface of the porous medium instantly reaches equilibrium with the gas phase, the following is reached (t > 0):
 (13)
(13)
From the discussions presented and based on the characterization results, there are preliminary indications that both vapor diffusion and liquid diffusion, caused by different mechanisms, are present in the drying of the porous media evaluated. It is necessary to know the activation energy in order to identify which are the predominant mechanisms for liquid diffusion, for example. Low values of this parameter (13 - 25 kJ/mol) show that superficial liquid diffusion is the limiting mechanism [9]. Still according to the same authors [9], the Knudsen number (Kn) can be obtained to identify if effusion is the limiting mechanism of the process. The Knudsen number is defined by Equation (14).
 (14)
(14)
5. Determination of the Preponderant Moisture Transfer Mechanism
The results of the estimation of effective diffusivity for the mass transfer mechanisms are shown in Tables 4 and
5. Vapor diffusion and effusion were calculated with Equations (6) and (8), respectively, and liquid effusion was calculated with the Arrhenius relationship, whose parameters (Ea and D0) were estimated in computational routines developed in Matlab code following the least square criterion. Equation (6) was incorporated into the diffusive model (Equation (10)) in order to estimate the parameter of the Arrhenius correlation. The analytical solution for the model was used [10] considering the 2000 first terms of the series. The analytical solution was obtained using the boundary and initial conditions presented in Equations (11) to (13).
From the data presented in Table 4, it can be seen that particle diameter does not significantly influence the vapor effective diffusion. The reason for these results to have been reached is that alumina particles do not present structural differences among each other. This is proven by the characterization studies performed. It was observed that the data which provide structural characterization of the particle show close results, such as those presented in Table3 Tortuosity values also had little variation regarding particle diameter. The greatest difference observed was of 0.0056. Therefore, once ordinary vapor diffusion is dependent on the internal structure of particles and these presented similar characteristics for the diameter assessed, it can be inferred that the way moisture spreads inside the porous matrix is the same for both cases analyzed. The proximity of the values found for ordinary vapor diffusivity associated with the fact that this phenomenon presented more significant values when compared to the other mechanisms, suggests that this is not the mechanism that limits the drying of porous media. This means that effective ordinary vapor diffusion did not have major influence on the difference among the drying kinetic curves presented in Figure 2.
Influence of particle diameter was more significant in the vapor effusion phenomenon. This suggests that

Table 4 . Diffusion, effusion and Knudsen number.

Table 5. Liquid diffusion and ordinary parameters of Arrhenius equation.
moisture, when spreading in the interstices of the porous matrix as vapor, may encounter a certain internal structure that influences the collision of water vapor molecules with the pore walls. For the particles of 4 mm in diameter, for instance, in which the pores are less narrow, collisions of water vapor particles with the wall are less intense, and resistance to vapor transfer is lower, when compared to the results for the particle of smallest diameter (Dp = 2.80 mm). Consequently, higher values of diffusivity appear, even when considering that all molecules travel at the same velocity. By comparing the results obtained for vapor diffusion and effusion, it can be observed that effusion, when it comes to moisture movement in the vapor phase inside the porous matrix, is the limiting mechanism, once it presented the lowest values. On the other hand, with a fast look at the data shown in Figure 2, it is possible to verify that moisture evaporates more quickly for porous media consisting of the smallest particle diameters. This contradicts the results presented in Figure 4, which show that vapor effusion is higher for particles of larger diameters. Even if Knudsen diffusion is present in the drying of porous media consisting of alumina spheres, according to the results of particle pore distribution and to the literature [9], it may not yet be the limiting mass transfer mechanism in the drying process.
This analysis is reinforced by the low values obtained for the Knudsen number. From the results shown in Table 4, it can be seen that the values of Kn are smaller than the unit for all presented cases. This indicates that Knudsen diffusion is not a significant mechanism (even though it is present in the drying process), but that another diffusive mechanism limits the migration of moisture inside the porous matrix: liquid diffusion. This fact is even better proven when all obtained values of effective diffusivity are compared. It can be observed that effective liquid diffusion (ordinary or superficial) presented the lowest values among all moisture diffusion mechanisms. This is information that reinforces the fact that the drying process at decreasing drying rate is controlled by liquid diffusion. At this point, it is necessary to know which liquid diffusion mechanism limits the process and is, thus, responsible for favoring different moisture curves as a function of time as presented in Figure 2.
From the data presented in Table 5, it can be verified that particle diameter has an influence on how the liquid is spread throughout the porous matrix. Resistance to liquid diffusion is greater for the particle with larger diameter, which indicates that diffusion is inversely proportional to the resistance imposed by the medium. This not only agrees with the literature [11], but also with the experimental results presented in Figure 2. It can be observed that the movement of liquid in the pores is greater for smaller particle diameters by interpreting the parameter D0 as the liquid mobility through the interstices of the solid matrix. Therefore, for porous media consisting of particles of smaller diameters, the resistance imposed to the liquid by the structure of the medium itself is lower and moisture replacement on the surface happens more rapidly, which favors a greater vapor flow in this region.
Particle diameter did not significantly influence the activation energy, possibly because this parameter is mainly associated with the influence of operational conditions, as shown by Perazzini, Freire and Freire [12]. Under the same operational conditions, as presented in Table 5, the energy required to remove 1 mol of pure water present in the material is similar for all media studied. It is also possible to observe that the estimated values of activation energy are lower than 13 kJ/mol, as described by Baini and Langrish [9]. The low activation energy values indicate that superficial diffusion of the liquid molecules throughout the surface of the capillaries is the limiting mass transfer mechanism in the drying process. In this case, the liquid molecules strongly interact with the walls of the pores moving along them during the drying process. Interaction of molecules with the wall is due to the fact that the mean free path of molecules is larger than the diameter of the pores [5]. When it comes to the drying of media consisting of alumina particles, this interaction is even greater for the superficial diffusion than for superficial effusion. According to Baini and Langrish [9], what actually proves superficial diffusion as limiting phenomenon is the fact that the low activation energy values obtained are lower than the energy values needed to evaporate moisture (45 kJ/mol). This implies that moisture may be transported along the capillary walls through chemical and physical interactions with the solid.
In terms of mathematical modeling, especially when the pseudo-homogeneous approach is used to represent the experimental data, Ficks’s model, based on the diffusion theory, can be used to simulate the data observed, where, for the porous media and operational conditions evaluated, the overall effective diffusion coefficient can be approximated by:
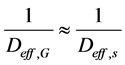 (15)
(15)
6. Conclusion
In this work, the drying kinetics of three different porous media was studied based on the concept of effective moisture diffusion. The characterization of the particles that constituted the media was performed and information to estimate diffusivity based on different mass transfer mechanisms was obtained. Moisture data as a function of time showed that each porous medium studied has distinct drying kinetics influenced by the characteristics of particles which form the medium. It was verified that the diffusive mechanism that limits moisture transfer inside the porous matrix is the effective superficial liquid diffusion, which indicates that moisture is mainly transported along the walls of the capillaries through chemical and physical interactions with the solid. From these results, it is possible to infer that the diffusive model, based on Fick’s Second Law of diffusion, is appropriate to represent the experimental data of the drying process.
Acknowledgements
The authors thank CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico) for the financial support.
NOTES