An Extended Model of Currency Options Applicable as Policy Tool for Central Banks with Inflation Targeting and Dollarized Economies ()
1. Introduction
In spite of the very recent debate in Caballero [2], Good friend [3], Taylor [4,5] and Woodford [6], on some limitations on how to apply it, the well-known Taylor-rule for inflation targeting (IT) has to be recognized as one of the most fruitful tools provided by macroeconomists to facilitate predictability and credibility related to changes in future price level. It is also claimed that for IT to be successful is required to include a high degree of exchange rate flexibility as in Ostry, Ghosh and Chamon [7]. In today’s world, emerging markets economists and policy makers are no longer engaged in just choosing an exchange rate regime as a framework for the economic activity in a country, but rather to optimize growth, employment and private investment. In that sense, the adoption of the Taylor-rule for IT has become not only fashionable but also useful to relate the effects in the nominal interest rate with the desired and observed levels of inflation, changes in the Real GDP and the short-term trends in the business cycle, as seen in Apergis, Miller, Panethimitakis and Vamvakidis [8], and Salvatore [9,10].
There are, however, some potential long-term weaknesses and yet unresolved policy issues when applying IT to dollarized economies. Ozsoz, Rengifo and Salvatore [11] show additional challenges for the policy-makers that come from the dollarization phenomena and the potential currency competition. It brings complex situations, where the effectiveness of the monetary policy may appear partially or temporarily restricted, opening the case for increasing imbalances that may precipitate financial crises in the medium-term, with massive inflows of foreign speculative capital and abrupt local currency appreciation.
The use of market-related tools, such as currency options, is not strange to literature (see Veestraeten [12]), although they have been just partially employed in a few countries, and none has attempted to merge currency option models, such as the Garman-Kohlhagen [1], within an IT framework.
There are some cases that will help us to set the boundaries of this proposed research. As seen in works of Archer [13], Bernedo and Azañero [14], Breuer [15], Gürsu and Öncü [16], Mandeng [17], Orellana and Rodriguez [18], Suk and Malliaris [19], Taylor [20], and Uribe and Toro [21], there is some recent evidence to assume that exchange rate intervention by employing market-friendly tools such as currency options, can provide the additional instruments many central banks in small dollarized openeconomies, are looking for.
2. The Model
We will employ the model presented by Taylor [22], Molodtsova and Papell [23], where the most widely used expression by central banks is usually written as:
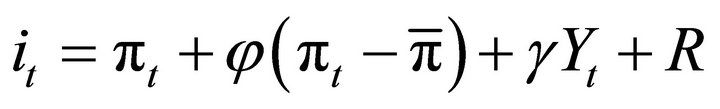 (1)
(1)
where  is the policy target domestic interest rate,
is the policy target domestic interest rate,  is the actual inflation rate,
is the actual inflation rate,  is the target inflation rate,
is the target inflation rate, 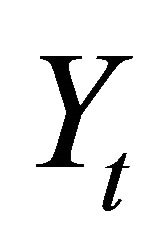 is the Output gap (potential vs actual real GDP), and R is the equilibrium real interest rate.
is the Output gap (potential vs actual real GDP), and R is the equilibrium real interest rate.
Rearranging some terms to obtain a form easier to compute, we get:
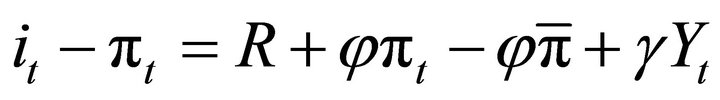 (1.a)
(1.a)
by separating in two terms, we get:
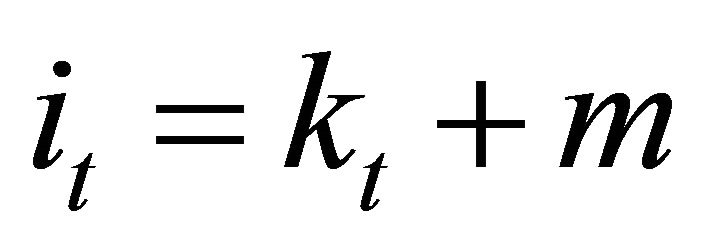 (1.b)
(1.b)
where 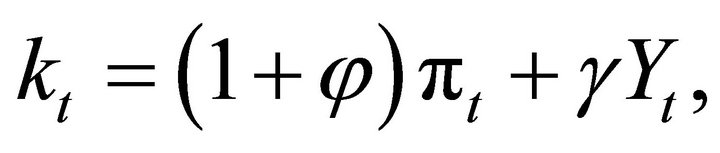 (1.b.1)
(1.b.1)
and 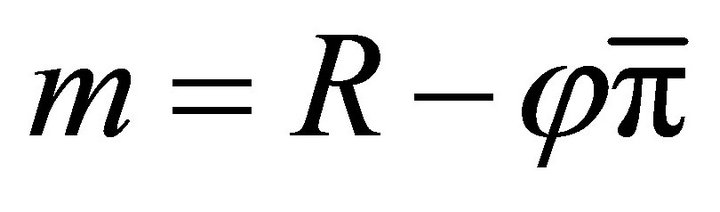 (1.b.2)
(1.b.2)
As a suggestion to avoid multicollinearity, the regressional form may be set as:
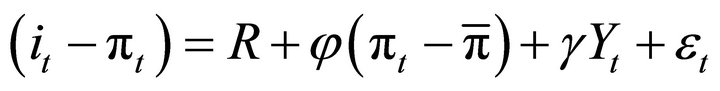 (1.a.1)
(1.a.1)
After obtaining the fitted values for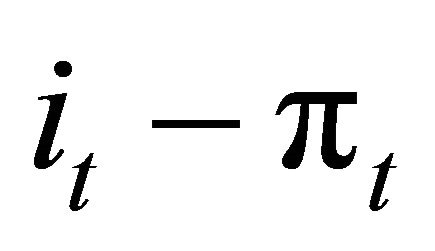 , and then substracting
, and then substracting , we obtain
, we obtain  as the estimated target nominal interest rate.
as the estimated target nominal interest rate.
Renaming the terms and using T (for Taylor) instead of t for the purpose to identify them as instrumental values that come from the Taylor expression, the estimated regression can be written as:
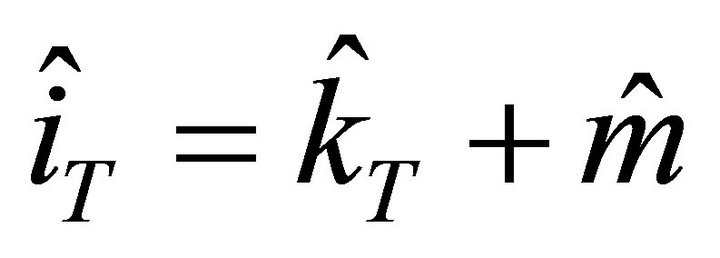 . (2)
. (2)
Whereas, by grouping terms from (1.a.1), we get:
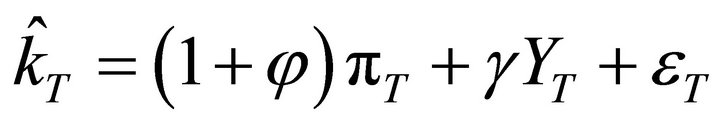 (2.a)
(2.a)
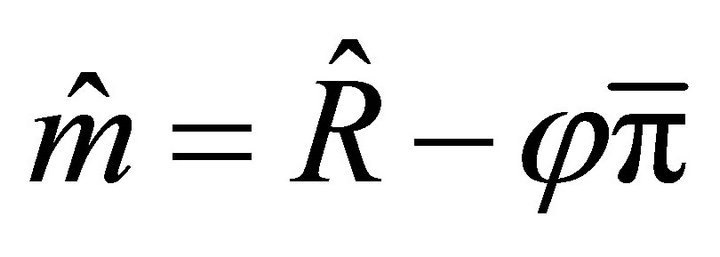 (2.b)
(2.b)
Being the Garman-Kohlhagen (GK) model an European option, with q being the risk-free foreign interest rate, and Ф(d), the cumulative distribution function for the standard normal distribution, the values 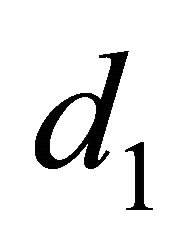 and
and 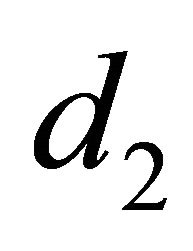 of the GK formula with the coefficients from the Taylorrule, the modified
of the GK formula with the coefficients from the Taylorrule, the modified 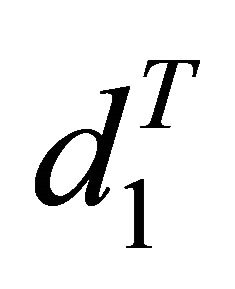 and
and 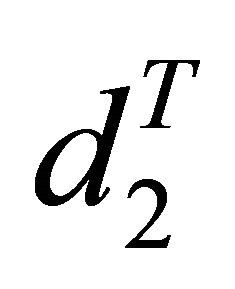 are:
are:
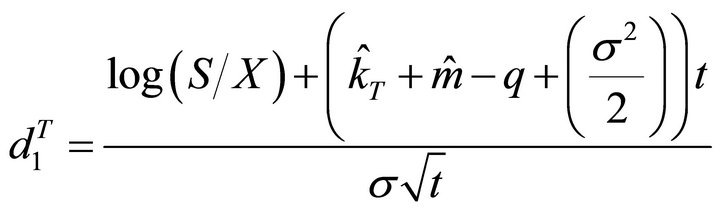 (3)
(3)
and,
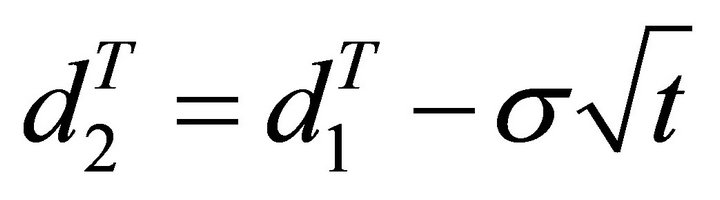 (4)
(4)
So, the expressions for the Call and the Put options of the GK-Taylor modified will be:
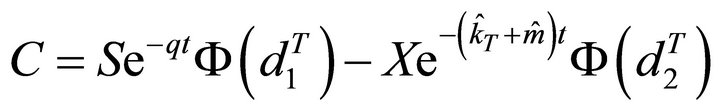 (5)
(5)
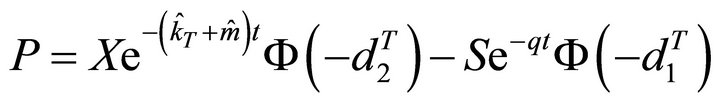 (6)
(6)
Being log the natural logarithm, and:
S = the current exchange rate (domestic currency per unit of foreign currency);
X = the strike exchange rate;
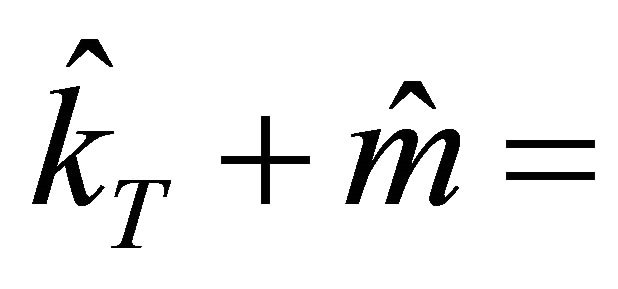 the estimated domestic target interest rate
the estimated domestic target interest rate 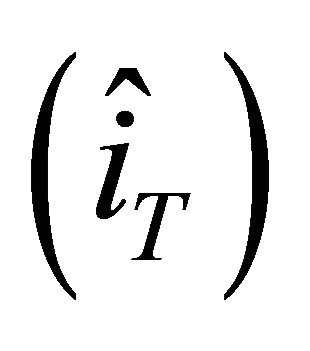 by the Taylor-rule regression;
by the Taylor-rule regression;
q = the continuously compounded foreign risk-free interest rate;
t = the time in years until the expiration of the option;
σ = the implied volatility for the underlying exchange rate;
Φ = the standard normal cumulative distribution function.
Assuming option values at expiration time E to be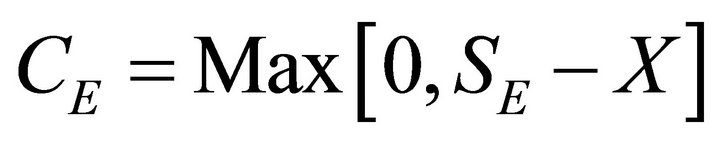 , and
, and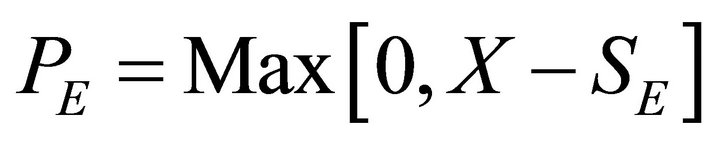 , options having non-negative prices such as
, options having non-negative prices such as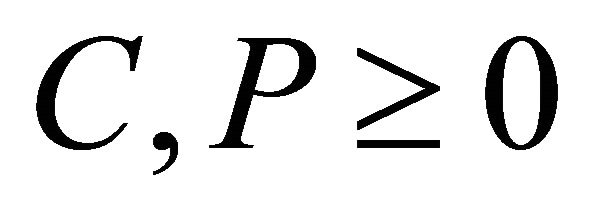 , upper boundaries
, upper boundaries 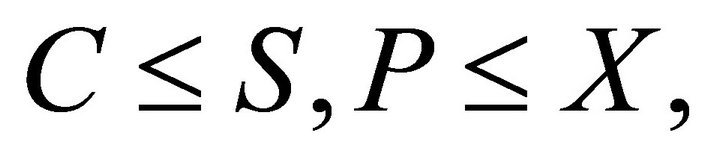 and lower boundaries
and lower boundaries 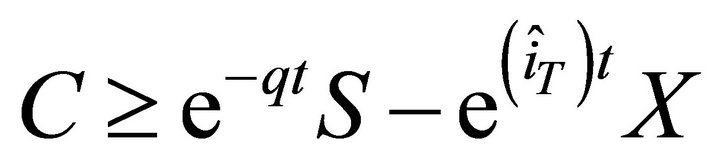 , and
, and 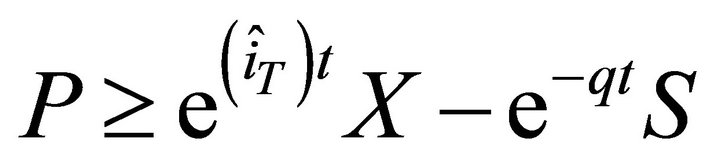 , as described by DeRosa [24], as well as Haup [25] and Steland [26], for further details.
, as described by DeRosa [24], as well as Haup [25] and Steland [26], for further details.
3. First and Higher Order Partial Derivatives
In terms of the GK-Taylor modified model (GK-T), the new “Greeks” are defined in the following way:
Delta (Δ): 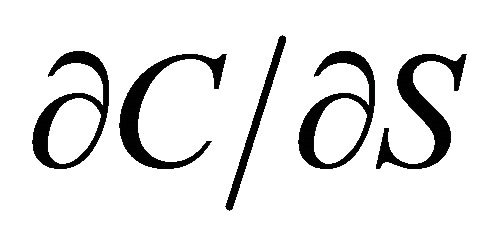 and
and 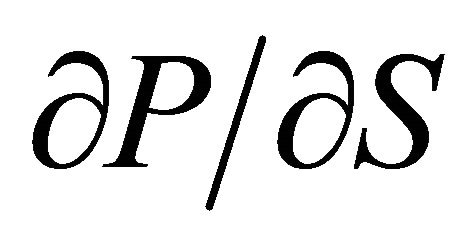 will show the change in the price of a corresponding Call or Put to the change in the price of the underlying asset. Delta is known as the “hedge ratio”, since it indicates how much of the underlying asset needs to be bought or sold to hedge the option.
will show the change in the price of a corresponding Call or Put to the change in the price of the underlying asset. Delta is known as the “hedge ratio”, since it indicates how much of the underlying asset needs to be bought or sold to hedge the option.
For a Call GK-T, 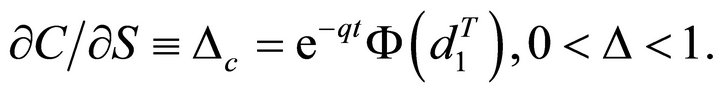
For a Put GK-T, 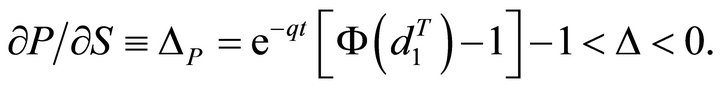
Gamma (Γ): It shows the amount that delta (Δ) changes of C and P when the underlying price changes, in this case S, the current spot exchange rate.
For the GK-T Call, 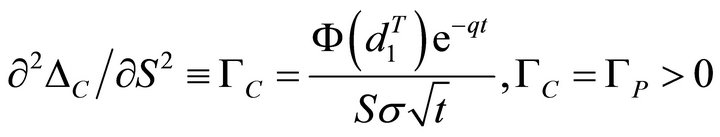
For the GKT Put, 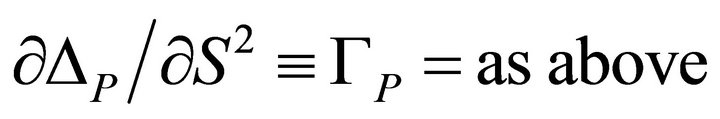
Vega (V): Vega is the amount that the theoretical value of an option changes when the volatility σ changes by one point (either money or percentage). So, 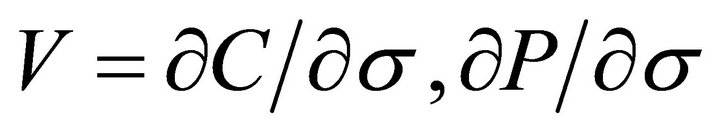 being C and P the values of a Call option and a Put option.
being C and P the values of a Call option and a Put option.
By deriving, we obtain
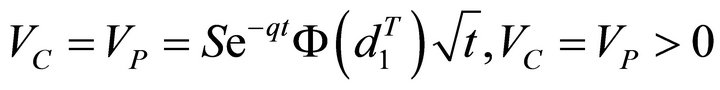
Theta (Θ): Theta represents the loss in value of the option in one time period, all other factors held constant. Then,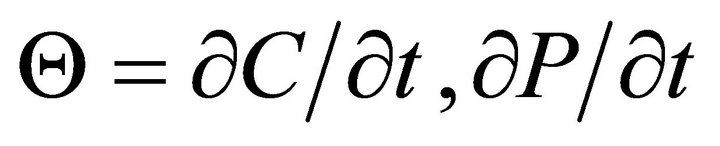 .
.
By deriving, we obtain the following expressions:
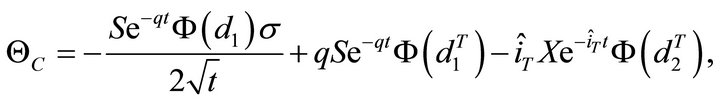
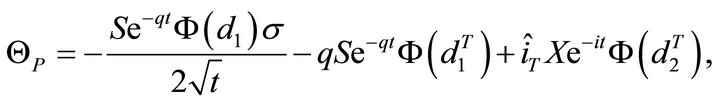
Being usually 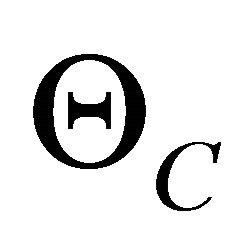 and
and ; and
; and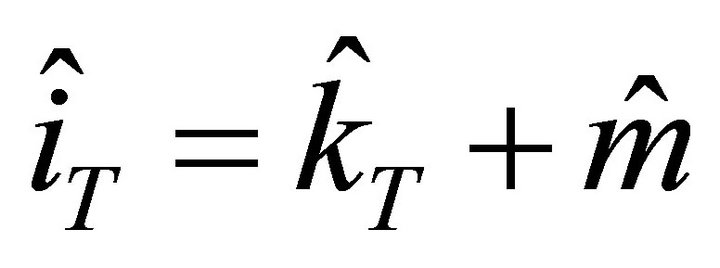 .
.
Rho (ρ): We will obtain several “rho” values for the GK-T model, since we have a domestic target interest rate 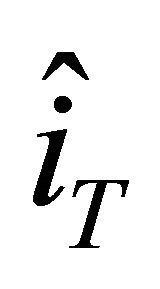 that depends on π and Y, and a foreign q interest rate. Rho is the change in the option price when there is a change in the interest rates. They may be critical for this research, since an important outcome of the “blended” IT model will rely on the central bank’s ability to operate either open or “shadow” currency options, to stabilize the trend of the exchange rate by minimizing the loss of the inflation target forecasting. Then, rho
that depends on π and Y, and a foreign q interest rate. Rho is the change in the option price when there is a change in the interest rates. They may be critical for this research, since an important outcome of the “blended” IT model will rely on the central bank’s ability to operate either open or “shadow” currency options, to stabilize the trend of the exchange rate by minimizing the loss of the inflation target forecasting. Then, rho 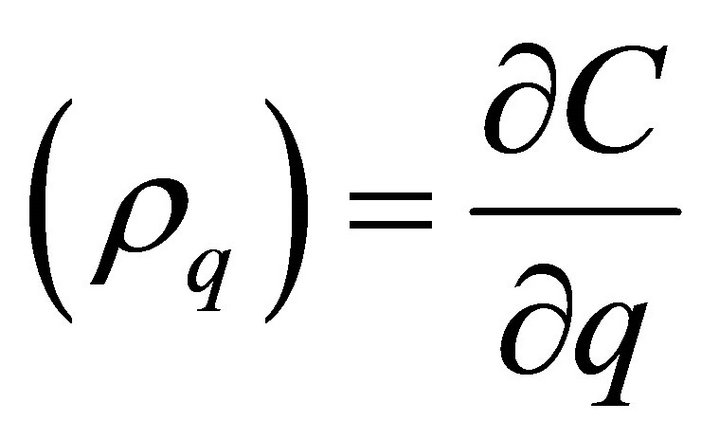 will be the first derivative of the Call option price when there is a change in the foreign risk-free interest rate.
will be the first derivative of the Call option price when there is a change in the foreign risk-free interest rate.
Deriving accordingly, we obtain:
1) For domestic rho, we will derive 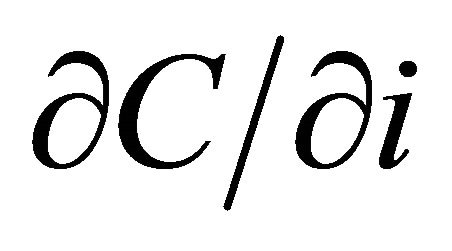 and
and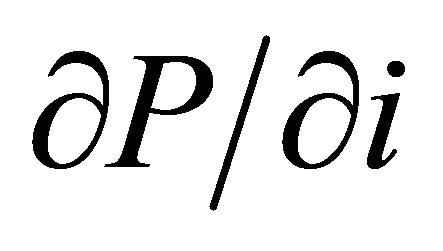 , as well as in terms of π and Y, such as
, as well as in terms of π and Y, such as 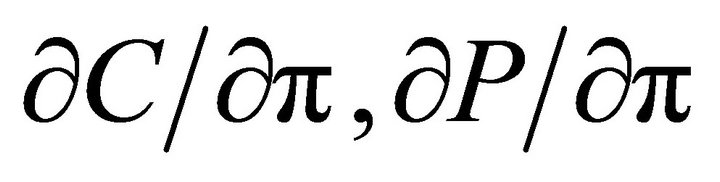 and
and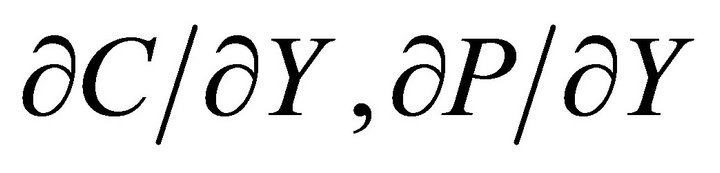 , so
, so
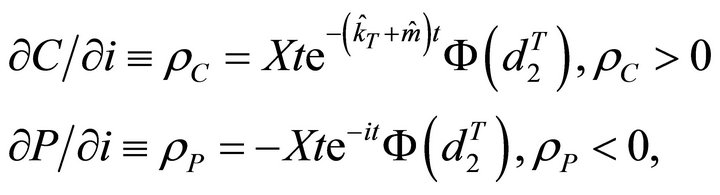
Since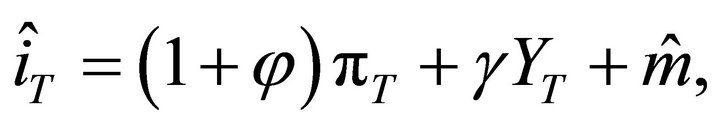 , then
, then
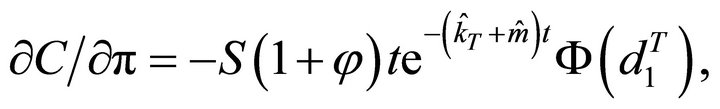 and,
and,
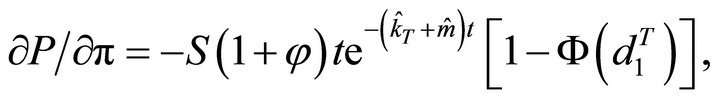 while
while
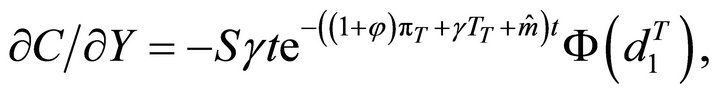 and,
and,
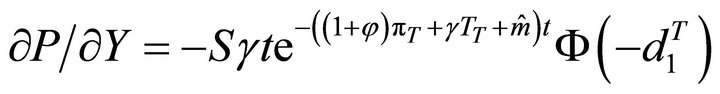
2) For foreign rho,
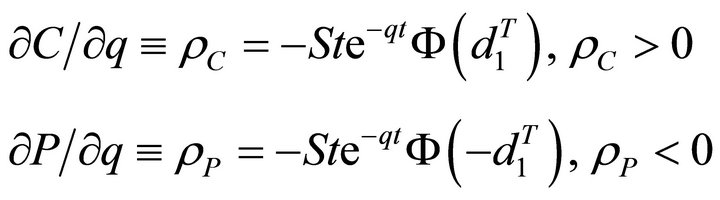
Useful higher order partial derivatives for C and Psuch as Vanna 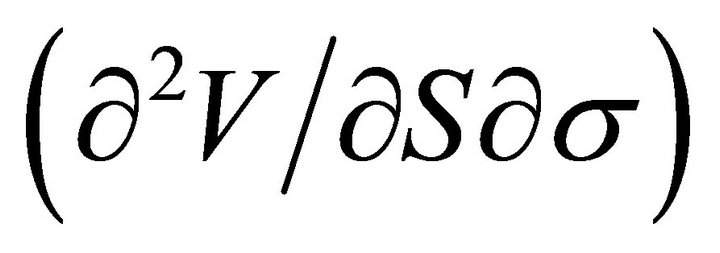 , Volga
, Volga 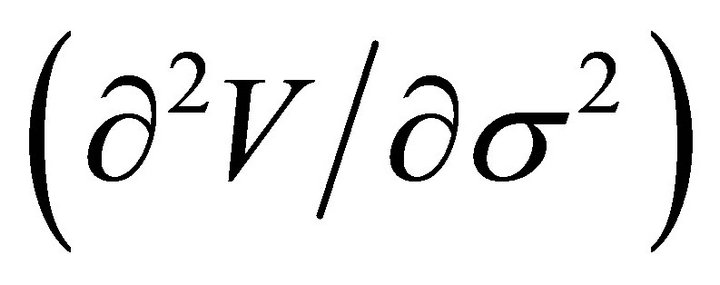 , Speed
, Speed 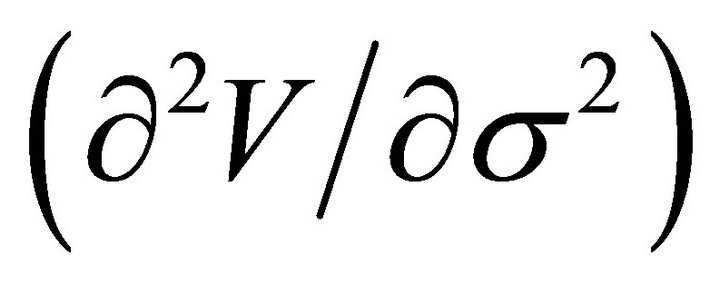 , DvegaDtime
, DvegaDtime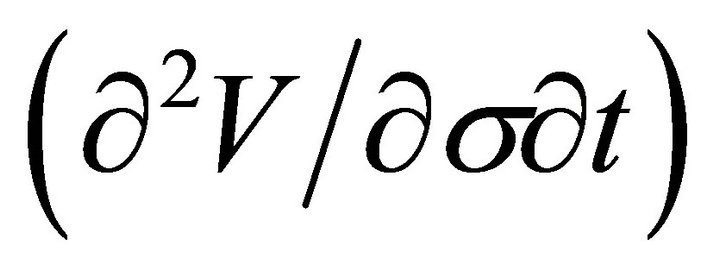 , and new “Greeks” (as in Arizmendi [27]), such as DrhoDpi
, and new “Greeks” (as in Arizmendi [27]), such as DrhoDpi 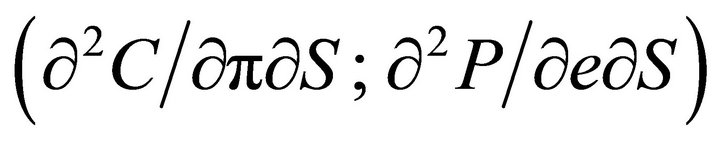 , and DrhoDoutput
, and DrhoDoutput 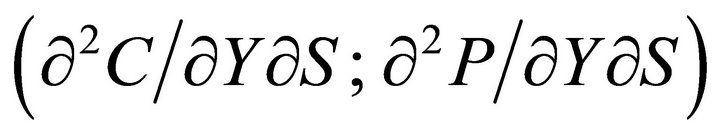 , are also obtained as:
, are also obtained as:
Vanna 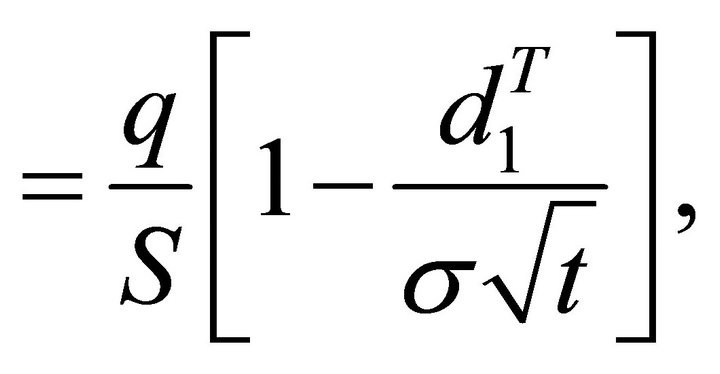
Volga 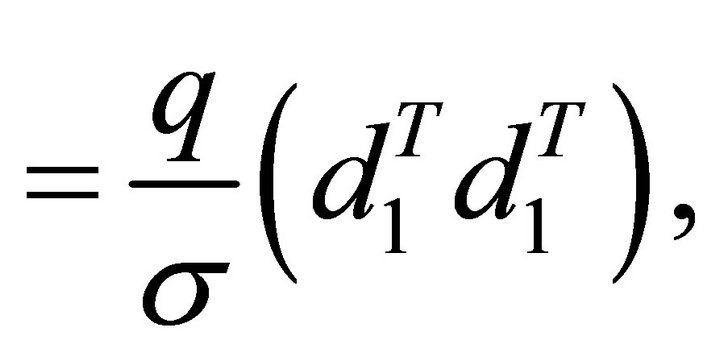
Speed 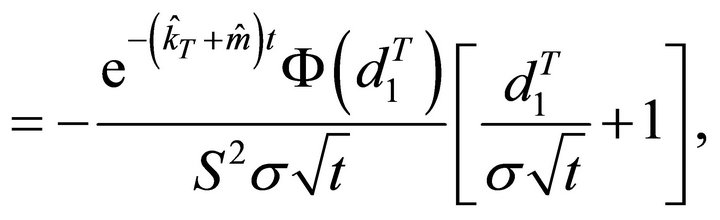
DvegaDtime
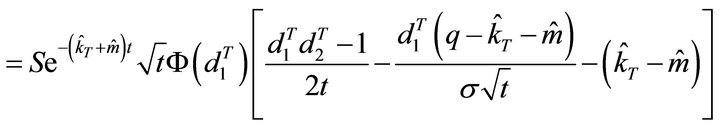
DrhoDpi (Call)
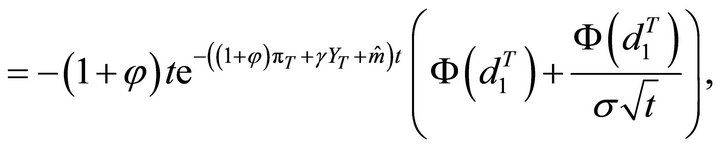
DrohoDpi (Put)
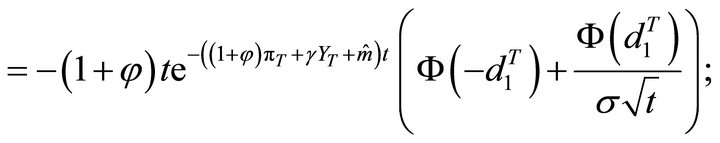
DrhoDoutput (Call)
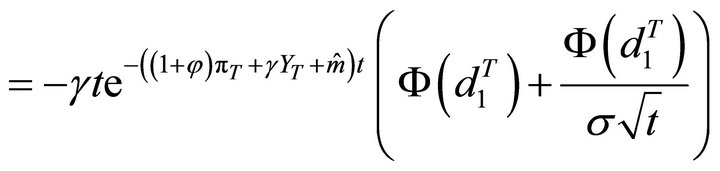 , and
, and
DrhoDoutput (Put)
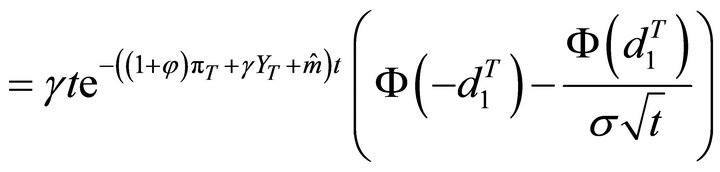
4. Conclusion
This model may be a useful set of tools for central banks and monetary authorities, especially those in countries with a relatively high level of dependency to a foreign currency, mainly through its local financial market and capital inflows. In particular, Call and Put option pricing—even if such derivatives market is not yet developed—may help central banks to intervene in the FX market when a combination of undesirable or untenable interest rate differentials, persistent inflows of capital, or a series of speculative attacks against the foreign currency in the local FX market, may cause the local currency to appreciate beyond certain level, introducing elements of potential instability, precisely opposed to what is sought by using the IT approach. In a free-float to dirty-float spot FX environment, the central bank of any given relatively dollarized country may diminish the cost of some sterilization through open-market-operations by calculating the relative value of its equivalent currency options, corresponding hedging and timely intervention.
5. Acknowledgements
The author wants to express its gratitude for the comments provided by Dominick Salvatore and Erick Rengifo, both at the Department of Economics, Fordham University, as well as Gianfranco Aguirre, Yerson Salcedo and Gabriel Samanez, from GPI Management S.A., that assisted him throughout the process of creating and writing this paper.