Application of Solution Calorimetry to the Prediction of 20.15[(2.038 + x)SiO2-(1.457 - x)Na2O]-2.6-P2O5-26.95CaO Glass Bioactivity ()
1. Introduction
In recent decades, the applications of bioactive glasses as bioimplants to repair damaged or diseased bones have escalated, particularly in the context of their ability to form a strong interfacial bond with living tissues. These glasses have been used in many clinical operations during the last twenty years including surgery of human body parts such as ears, teeth, knees and hips. The choice of bioactive glasses for implant applications requires design optimized compositions [1]. Thus, preparing bioactive glasses with different compositions, and evaluating their physicochemical properties, structural properties and chemical stabilities is crucial for the subsequent optimization of their biocompatibility [2,3]. Some compositions of glasses in the system SiO2-Na2O-CaO-P2O5, used as biomaterials, are able to form a bond with bone once they are implanted, such as the Bioglass [4,5]. The main advantages of these synthetic biomaterials are availability, reproducibility and reliability [6].
On the other hand, the synthetic biomaterials must be fully biocompatible, they should not generate any complication or inflammatory response, and also, they must be suitable in their mineral compositions. A common characteristic of all known bioactive materials is the formation of a biologically active HCA [7-9] layer in the presence of in vivo body fluids or in vitro simulated body fluids (SBF). SBF solution mimics the inorganic composition of human body fluids. The kinetics of the dissolution of the glass in the biological environment and consequently the bioactivity of the upper thin layer depend on the chemical composition of the glass [10,11].
In this work, synthesis of bioactive glasses was carried out by using the melting and rapid quenching technique. Samples in the system 20.15[(2.038 + x)SiO2-(1.457 − x)- Na2O]-2.6-P2O5-26.95CaO were studied over the whole composition range, using X-ray diffraction, pycnometry, differential scanning calorimetry and solution calorimetry according to the composition. The properties such as density, glass transition temperature and chemical stability were closely studied and correlated to changes in the structure and the evolution of the index of bioactivity by Andersson.
2. Experimental
Nine different glassy compositions belonging to the system 20.15[(2.038 + x)SiO2-(1.457 − x)Na2O]-2.6-P2O5- 26.95CaO were prepared by the melt quenching technique, as shown in Table 1.
High purity reagent grade silica (SiO2, Merck product)Table 1. Compositions in mol% (wt%) of glasses investigated.
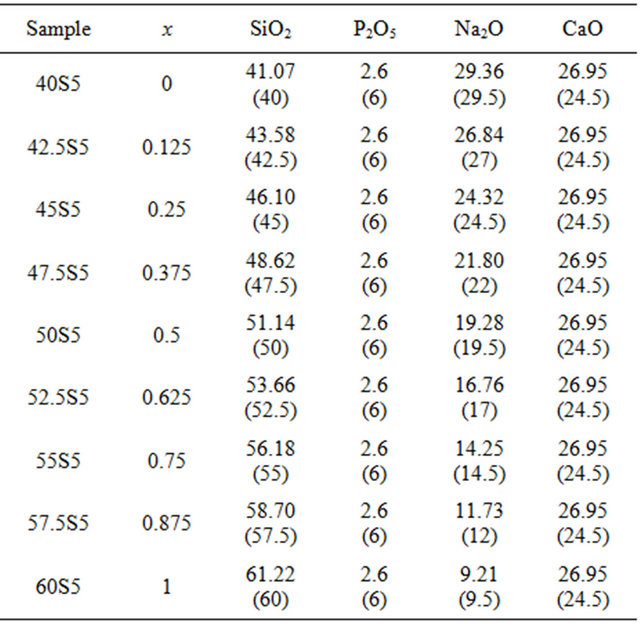
calcium carbonate (CaCO3, Prolabo product), sodium carbonate (Na2CO3, Aldrich product) and di-ammonium hydrogen phosphate ((NH4)2HPO4, Prolabo product) were used to obtain the glass compositions. These reagents were mixed up in the desired proportions and thoroughly ground in an agate mortar. The mixtures were fired in air in a platinum crucible using a programmed kiln, in the following manner:
a) Reaching 500˚C at the end of 80 min and maintaining this temperature for 30 min to allow the evaporation of water from the powders to be as complete as possible;
b) Reaching 1000˚C in 85 min and maintaining this temperature for 30 min to allow all the gases removal (CO2, NH3, H2O);
c) Reaching 1500˚C in 85 min and maintaining this temperature for 90 min to allow a complete homogenization of the melt.
The melt was quenched by dipping the bottom of the crucible into cold water. The resulting glass fragments were transparent and free from bubbles. The samples were then kept in vacuum desiccators in the presence of P2O5 to avoid possible moisture sorption before testing.
The amorphous state of our samples was analyzed by X-ray diffraction. The diffractograms were recorded between 10˚C and 60˚ (2θ) at a scanning speed of 2˚/min and a fixed step-size of 0.02˚ using a D5000 SIEMENS diffractometer with λ = 1.5406 Å and a tube voltage of 40 kV. The samples were all analyzed in powder form.
The glass transition temperatures (Tg) were measured by a differential scanning calorimeter (DSC 111 SETERAM). The mass of each analyzed glass sample was ~50 to 60 mg so that the curve obtained by DSC is operative. The handling was carried out under an atmosphere of argon in a crucible made of stainless steel seam. The heating rate was 5˚C/min. The rise in temperature is limited to 700˚C in order to keep the apparatus in good working condition. The values of the temperature (Tg) were given with an accuracy of ±3˚C.
Densities of glass samples were estimated at 296.15 K by using a pycnometer with diethylphtalate (d = 1.118) as the immersion fluid. The pycnometer consists in glass flask with a close-fitting ground glass stopper surmounted by a capillary indexed tube. This tube releases a part of the liquid after closing the top-filled pycnometer and allows to measure with a very high accuracy, masses of constant volumes of working liquid or liquid and solid. Care was taken to make sure that all of the cast samples were bubble free and that the glass samples were fully wetted when immersed in the diethylphtalate. All the weight measurements have been made using a digital balance Sartorius, having an accuracy of ±0.1 mg. The reported values of density are averages of the four to five independent measurements. Experimental accuracy in the density measurement is ±0.03 g·cm−3.
As the reaction between the glassy oxides cannot be carried out directly into the calorimeter at ambient temperature due to kinetic limitations, the well-known dissolution method is applied. This indirect method based on a Hess thermodynamic cycle consists in the successive dissolutions in the same solvent and at the same temperature of all the compounds involved in the reaction of formation [12-14]. HF calorimetric experiments were performed with a swinging calorimeter. The calorimeter and standard procedures have been described previously [14, 15] and so only a brief description will be given below. Thermopiles consisting of hundreds of chromel-alumel thermocouples were inserted into an aluminum block isotherm. The high stability of the device allows very long period of experimentation around room temperature (293 - 350 K). The whole measurement cell, made of Poly Tetra Fluoro Ethylene (PTFE) resin allows dissolutions in all mineral acidic or basic aqueous solutions. The stirring rate was 3 rpm. The calorimeter is in a thermally regulated room at ± 1 K and the dissolutions are carried out at 298.15 ± 0.01 K. Before dissolution, the solute and the solvent are whole isolated each other in two distinct compartments separated by a platinum cap and a n-decane liquid joint. The acidic vapor cannot react with the solute during the thermal stabilization time of the calorimeter. After thermal equilibrium during about 4 h, the solute is put in touch with the solvent which consists in a 4 mL HF (6 M) and 4 mL HNO3 (4 M) mixture by rotating the calorimeter. The dissolution starts with the first rotation. The rotation of the calorimeter is stopped as soon as the flow of energy produced by the reaction is cancelled. The data acquisition is stopped about an hour after the end of the dissolution so the final thermal and mechanical state of the calorimeter is identical to the initial state. The calorimeter was calibrated by using the heat effect of the well-known enthalpy of dissolution of tris-hydroxy-methylaminomethane in hydrochloric solution [15].
3. Results and Discussion
3.1. Results
X-ray diffraction measurements at room temperature confirmed the amorphous state of the samples. DSC thermograms showed endothermic peaks in the temperature range 489˚C - 613˚C (Figure 1). These endothermic peaks are attributed to the glass transition (Tg), at which atoms start to be reorganized towards crystallization. The Tg data are gathered in Table 2 and shown as a function of the SiO2 content in Figure 2. The line is only drawn as a guide to the eye. It has been found that Tg increased from 489˚C to 613˚C with the increase in the SiO2 mole fraction from nought to one.

Figure 1. DSC curves for studies glasses.
Table 2. Measurements of the glass transition temperature (Tg), density (d) and molar solution enthalpy at infinite dilution  at 298.15 K of the 20.15[(2.038 + x)SiO2- (1.457 − x)Na2O]-2.6-P2O5-26.95CaO bioactive glasses.
at 298.15 K of the 20.15[(2.038 + x)SiO2- (1.457 − x)Na2O]-2.6-P2O5-26.95CaO bioactive glasses.

Measurements of the densities of the studied bioactive glasses are also listed in Table 2. Density is a quantity sensitive to the spatial arrangement and the nature of atoms [16]. Therefore, it depends on the composition. We observe the same decrease monotonically, from 2.79 to 2.66 g∙cm−3 with the addition of silica content in the mixture (Figure 3).
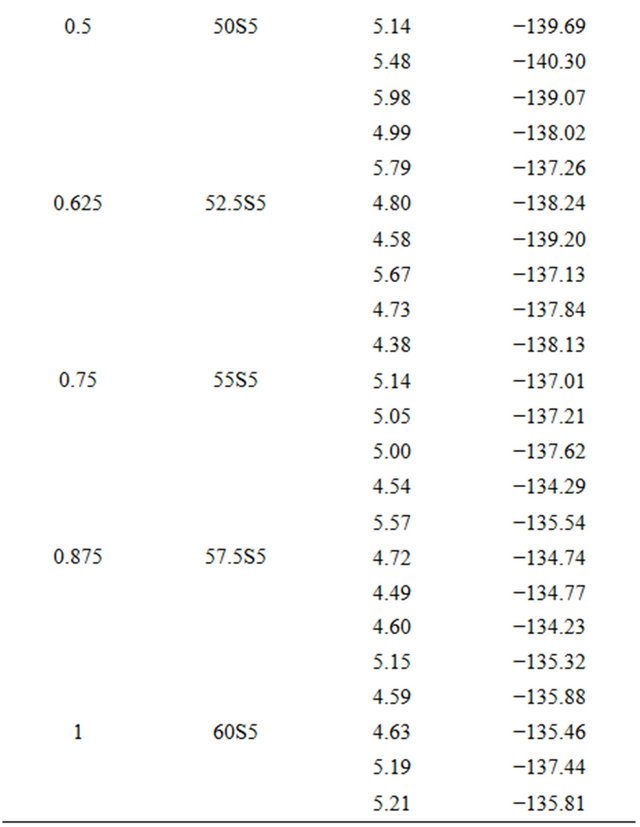
For each glass composition, the enthalpy of dissolution was measured five times at different solute concentrations. The results are summarized in Table 3. The enthalpies of dissolution are strongly negative and strongly exothermic. Table 2 shows the values of the enthalpy of dissolution at infinite dilution at 298 K. They were deduced by linear extrapolation to zero concentration enthalpies of dissolution for each glass composition. The accuracy of these estimations was about ±0.64 kJ·mol−1.
Classically, the enthalpy of formation determined by the dissolution method is obtained with the algebraic sum of the enthalpies of solution: Let AxB1−xC be a mixture of the A, B and C compounds in the same physical state at the same temperature:
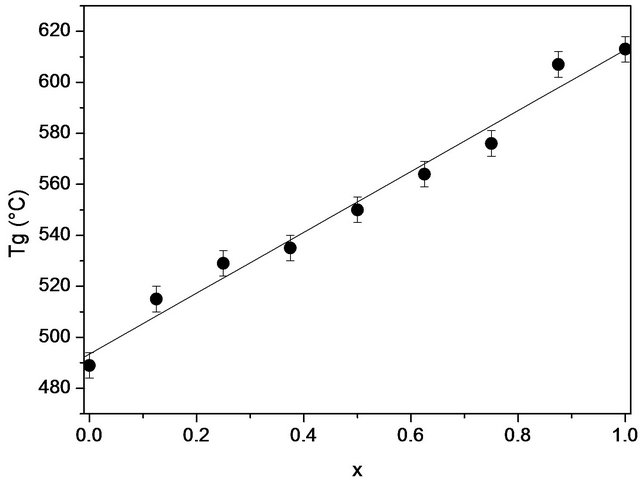
Figure 2. The variation of the glass transition temperature (Tg) of 20.15[(2.038 + x)SiO2-(1.457 − x)Na2O]-2.6-P2O5- 26.95CaO bioactive glasses with the silica content.

Figure 3. Variations of experimental densities with the composition (x) of the 20.15[(2.038 + x)SiO2-(1.457 − x)Na2O]- 2.6-P2O5-26.95CaO bioactive glasses.
Table 3. Measurements of enthalpies of dissolution of 20.15[(2.038 + x)SiO2-(1.457 − x)Na2O]-2.6-P2O5-26.95CaO bioactive glasses at 298K in 4 mL HF (6 M) and 4 mL HNO3 (4 M).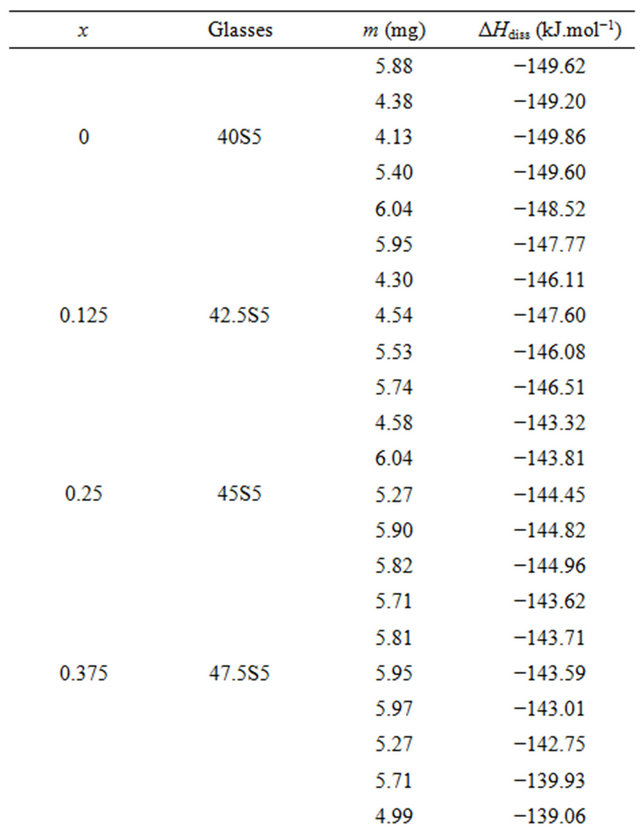

Let be the dissolution reactions extrapolated at infinite dilution at the same temperature and in the same solvent S, the ∆dissHi∞ being the enthalpies at infinite dilution previously calculated.
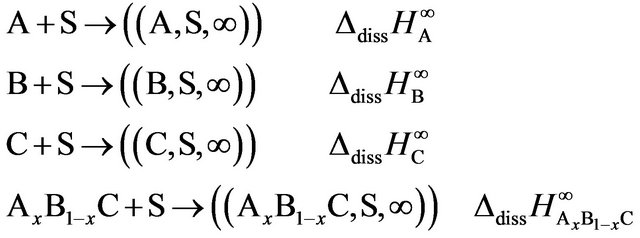
The enthalpy of formation is obviously calculated by:
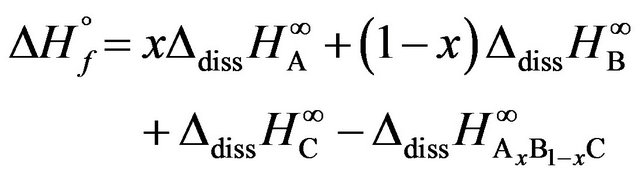 (1)
(1)
Because the interaction between the solutes at infinite dilution in the solvent S is null or:

Experimental measurements or estimated enthalpies of dissolution values of SiO2, P2O5, CaO and Na2O oxides necessary to the calculation of the enthalpies of formation are indicated to the Table 4.
These data are used to calculate the corresponding enthalpies of formation using Equation (1). The uncertainties in the enthalpies of formation are extracted from the errors in the enthalpies of solution. For condensed phases and ambient temperature, the entropic contribution  is small and negligible in comparison with that of the enthalpy of formation
is small and negligible in comparison with that of the enthalpy of formation . Therefore, the free enthalpy of formation
. Therefore, the free enthalpy of formation  can be equated to the enthalpy of formation
can be equated to the enthalpy of formation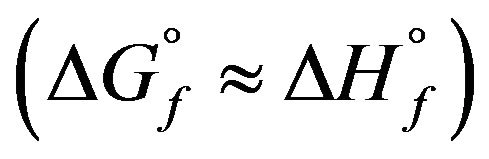 . The results are summarized in Table 5. The so calculated free enthalpies of formation are listed in Table 5 and reported on Figure 4.
. The results are summarized in Table 5. The so calculated free enthalpies of formation are listed in Table 5 and reported on Figure 4.
The materials studied (Table 1) showed interesting biological properties largely developed in the literature [17,18]. Our approach is part of a process of pre-evaluation of the bioactivity of a glass on the basis of a study by solution calorimetry with its thermodynamic stability.
Table 4. Experimental measurements or estimated enthalpies of dissolution  (kJ·mol−1) values of SiO2, P2O5, CaO and Na2O oxides at 298 K in 4 mL HF (6 M) and 4 mL HNO3(4M).
(kJ·mol−1) values of SiO2, P2O5, CaO and Na2O oxides at 298 K in 4 mL HF (6 M) and 4 mL HNO3(4M).
Table 5. Index of bioactivity (RN) and free enthalpies of formation at 298 K bioactive glasses system 20.15[(2.038 + x)- SiO2-(1.457 − x)Na2O]-2.6-P2O5-26.95CaO.


Figure 4. Variation of the free enthalpy of formation at 298 K as a function of the silica content of bioactive glasses 20.15[(2.038 + x)SiO2-(1.457 − x)Na2O]-2.6-P2O5-26.95CaO.
To achieve this, we calculated the free enthalpies of formation  of glasses in a solution of HF (6 M) +
of glasses in a solution of HF (6 M) +
HNO3 (4 M) at 298 K and obtained evidence of bioactivity following Andersson’s equation [19,20]:
 (2)
(2)
with the proportions of the oxides in weight percent. RN is the “Reaction Number”, a value permitting to define a domain of bioglasses. If RN is superior or equal to 5, then the glass develops apatite and bonds to bone. The results are also summarized in Table 5.
After eight weeks of in vivo experiments in rabbits’ shins, Andersson states that when: RN = 1, the lenses are virtually inert, and it was found that a slight change in the surface composition occured. For RN = 2, there is contact with the bone but no real connection. Also, a layer of silica gel was formed on the surface but there was no precipitation of CaP. As for RN = 3, the glasses are very soluble, there is contact with the bone but again no real connection. The silica-rich layer is well formed but the precipitation of CaP is low. Then, for RN = 4, there was the formation of a CaP-rich layer but not enough to create a strong bond with the bone. Finally, for RN = 5, there was the formation of a layer of hydroxyapatite and consequently bone binding. The bioactive glasses have an RN value equal to or greater than 5.
According to Table 5 glasses 40S5 (x = 0) and 42.5S5 (x = 0.125) are their RN higher than the Hench glass [4], reference glass called “Bioglass” noted 45S5 whose molar composition are 46.1% SiO2, 26.9% CaO, 24.4% Na2O and 2.6% P2O5, developing its hydroxyapatite layer after 12 hours immersion in contact with a physiological fluid. It is likely that these glasses are more bioactive than the Hench glass. Beyond the 52.5S5 composition, the link with the bone is weakened although in all cases, there is contact with the bone. In this study, the most bioactive glasses are poorer in silica and rich in sodium, in accordance with the work of Lebecq et al. [21].
With the results of the free enthalpies of formation given also in Table 5, we can assert that all compositions are very stable compared to their simple oxides at 298 K and their stabilities diminish gradually as the silica content increases in the system considered (Figure 4). Figure 5 reports the change in reactivity index based on the free enthalpy of formation of each glass. The physicochemical reactions that occur on the surface when tested in vitro follow a mechanism common to almost all bioactive glasses [22]. However, the chemical reactivity of the glass in contact with the simulated biological fluid may be strongly influenced by the free enthalpy of formation of the latter. The shape of the curve of Figure 5 for RN can be schematically divided into two zones, extensive variables defined by a change in chemical reactivity (slope change) on which the thermodynamic and physi-
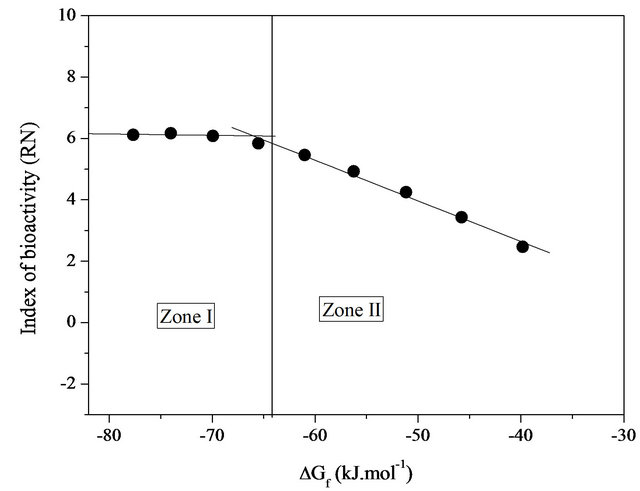
Figure 5. Variation of the index of bioactivity (RN) based on the free enthalpy of formation at 298 K bioactive glasses system 20.15[(2.038 + x)SiO2-(1.457 − x)Na2O]-2.6-P2O5-26.95CaO.
cochemical parameters can act and optimize the performance of bioactivity.
3.2. Discussion
The crystallinity of each obtained sample was systematically controlled by X-ray diffraction before any physicochemical analysis. The XRD results revealed that the samples are amorphous over the whole composition range in accordance with the work of L. L. Hench [23].
The glass transition temperature (Tg) plays an essential role in understanding the physical properties of bioactive glasses. In bioactive glasses, the glass transition temperature is particularly sensitive to the optimization of the composition of the bioactive glasses. All the samples studied herein were of the same thermal history and the same heating rate. Therefore, the cause of the changes in the Tg can be attributed to changes in the structure of the glass (Figure 2). Indeed, when the modifier oxide (Na2O) is replaced by the forming oxide (SiO2), molecular mobility is likely reduced because of the increase in the average degree of crosslinking. This increase is most likely a reflection of the building structure due to changes in composition. The creation of a network covalent character is favored by most orthophosphate groups which show no preferential association with Na+ and Ca2+, not used by non-bridging oxygens of the SiO4 tetrahedra.
Density is an effective tool for exploring the evolution of the structure, coordination and cross-linking of glasses. Indeed, the density of a glass is directly related to the density of the elements involved in the system. According to Figure 3, the density of the bioactive glass system studied decreases almost linearly with the molar concentration of SiO2 from 2.79 to 2.67 g·cm−3 without showing any abnormality. This result may suggest a change in the quasi-monotone structure due to the incorporation of SiO2 at the expense of Na2O in the glass. The quasilinearity of the curve of variation of the enthalpy of formation may be indicative of a very weak interaction of the silica with the polymer chain.
Changes in the proportions of RN revealed the various stages leading to the formation of a hydroxyapatite layer in a simulated physiological environment. The slopes for these variations may be associated with the reactivity (clashes) of the different glasses via their reactive surfaces. The area in which curve I based RN is almost constant indicates a maximum threshold of bioactivity in the system studied. In this field of enthalpy of about −80 to −65 kJ/mol, the superposition of the silica-rich layer and the layer of hydroxyapatite is clearly observable above the glass matrix (in solution). They are predisposed to generate a series of physico-chemical reactions that can promote the growth of apatite in contact with a biological medium, allowing interfacial chemical bond with a bone marrow. The hydroxyapatite layer is intimately connected with the bone. As for zone II, it marks a nearly linear decrease (drastically) of RN index with increasing free enthalpy of formation. It therefore appears that in this case, the stable bond between the material and the host tissue is reduced or inhibited.
Several reasons explain the biological activity of a glass. We can distinguish kinetic energy and morphological root causes. Justifications based on kinetics and morphology have been widely put forward to explain and improve the bioactivity of glasses. Our study also shows that the nature and composition of the glass determine the biological characteristics (index of bioactivity) of the material. It has been shown, the importance of the thermodynamic parameter as well as the morphology and the kinetics. The nature and the composition of the glass affect the thermodynamic properties of the glass and thus the heat transfer. A glass, of low-silica content, induces a substantial increase in the enthalpy of formation in reference to constitutive single oxides, which promotes the simultaneous formation of a CaP layer and a layer rich in silica with a highspeed reaction. For glasses containing between 48 and 52 wt% of SiO2, both layers are well separated: the layer of silica gel is formed first, and then the CaP surface develops [5,7]. This results in a decrease in the enthalpy of formation in the two systems. For glasses containing between 53 and 60 wt% silica, the enthalpy of formation becomes smaller in absolute value. In this case, the CaP layer does not form substantially.
4. Conclusion
It has been demonstrated in this work that in sodium and calcium phosphosilicate glasses given by 20.15[(2.038 + x)SiO2-(1.457 − x)Na2O]-2.6P2O5-26.95CaO from the Hench bioactivity diagram domain, the addition of the SiO2 content leads to a gradual increase in Tg and a decrease in density. The enthalpy of mixing is negative and weak in the whole composition range. The reaction for the formation of the glass is favored thermodynamically. Silica-poor compositions are more stable. However, with the Silica-poor compositions, the products may form the HCA quickly, kinetic (the fastest product to form, training time short HAC) and thermodynamic (product thermodynamically most stable) controls being achieved simultaneously. Indeed, bioactivity is strongly dependent on both kinetic and thermodynamic control of the starting glass. Thermodynamic control is really crucial for bioactive glasses; the more stable the sample, the higher the ability to bind strongly to bone tissues. It reflects a weak chemical interaction between the components of the oxides. This study contributes to the enrichment of existing data on bioactive glasses.
NOTES