Fisher’s Fiducial Inference for Parameters of Uniform Distribution ()
1. Introduction
In 1930 Fisher proposed an inference method based on the idea of fiducial probability [1,2]. Fisher’s fiducial inference has been much applied in practice. The fiducial argument stands out somewhat of an enigma in classical statistics. The enigma mentioned above need statistical scholar to solve.
Fisher’s fiducial inference for the parameters of a totality 
is discussed. The corresponding fiducial distributions are derived. The maximum fiducial estimators, the fiducial median estimators and the fiducial expect estimators of 
and 
are got. The problems about the fiducial interval, fiducial region and hypothesis testing are discussed.
The example below shows that Neyman-Pearson’s confidence interval has some place to be improved. Let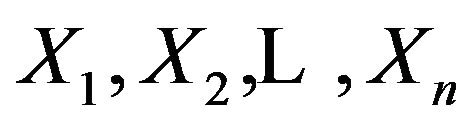 
be i.i.d., 
for each j.
. By [3] p. 16 Corollary 3.2 the density function of 
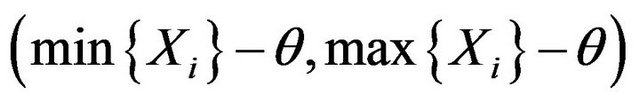is
Appling pivotal function
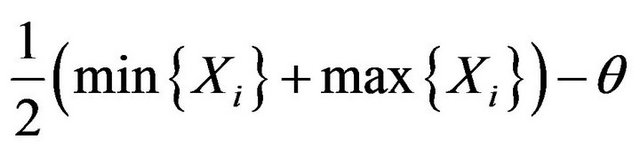
And using its density
the 95% confidence interval of 
can be got as
(*)
where 
is the solution of
The length of interval (*) is independent of the sample value! Assam that
Is got in a certain sample (Note that
the above data can illustrate the common problems). The probability that
i.e.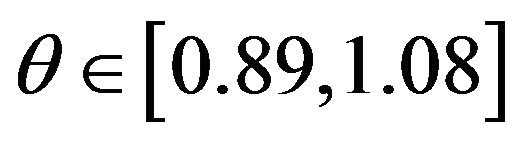
, is 1, the length of it is 0.19, but the length of (*) is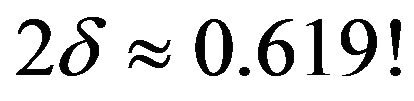 
Fisher’s fiducial inference offered a selection in solving the problems similar with above.
2. Fiducial Distribution
Let that 
is i.i.d.,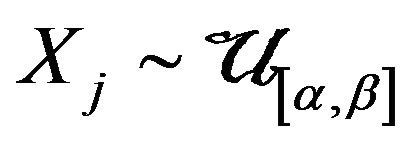
. As well known, their sufficient statistics of least dimension is
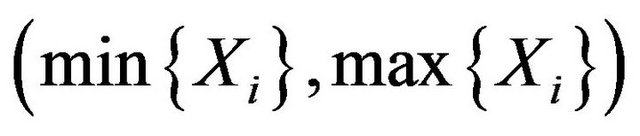.Set
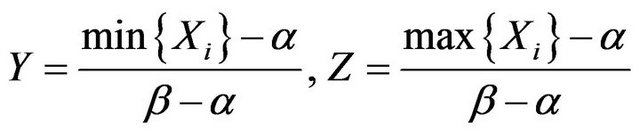(2.1)
It is not difficult to show that Y and Z are the minimum and maximum order statistics of the sample from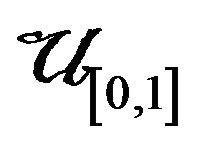 
respectively, and by [3] p. 16 Corollary 3.2, the density function of 
is
(2.2)
See parameters 
and 
as r.v.’s, see 
and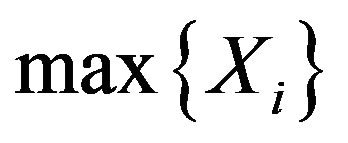 
as constants now. It can be got from Equation (2.1) that
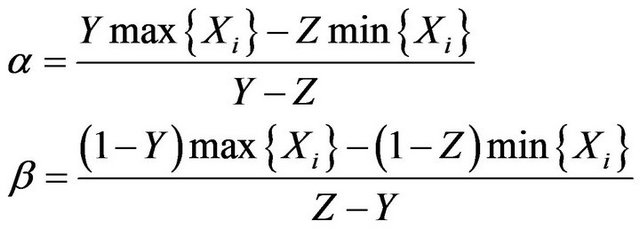(2.3)
Applying the relative results about the transformation of r.v.’s, it can be show that:
Theorem 1. The fiducial density function of vector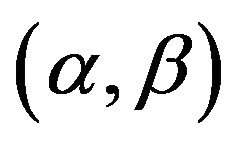 
is
(2.4)
If only one parameter need to be considered, the another parameter is then so-called nuisance parameter. We insist that the marginal distribution should be used in this situation. Hence find the two marginal density functions of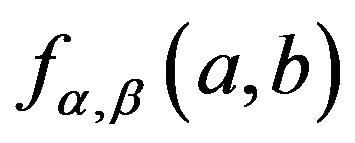 
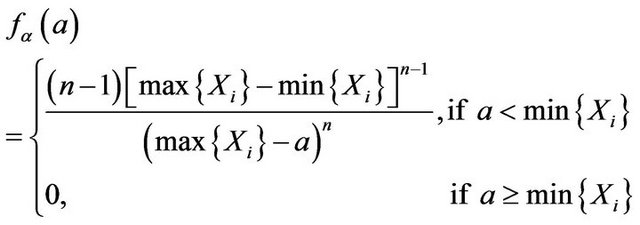(2.5)
(2.6)
Corollary 1. The fiducial density functions of only one parameters 
or 
as r.v.’s are given by (2.5) and (2.6).
3. Estimation
It is easy to see that fiducial density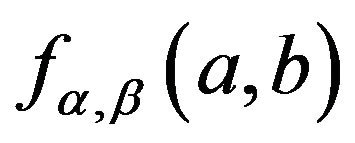 
has achieved its maxima at
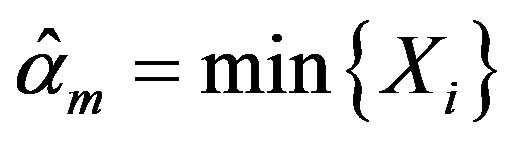(3.1)
(3.2)
Theorem 2. The maximum fiducial estimators of 
and 
are given by (3.1) and (3.2).
It can also be got that 
has achieved its maxima at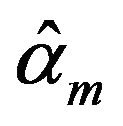
, and 
has achieved its maxima at 
as well. The estimators 
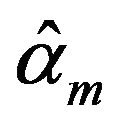and 
are coincided with the maximum likelihood estimators of 
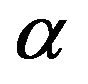and
.
To find the median of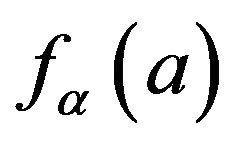
, solve
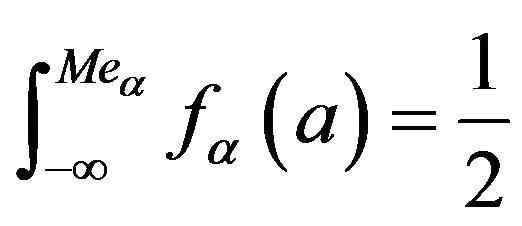(3.3)
And get
(3.4)
Found the median of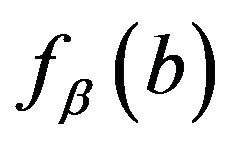 
by using the same method, and have
(3.5)
Theorem 3. The fiducial median estimators of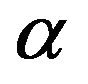 
and 
are given by (3.4) and (3.5).
The maximum fiducial estimators 
and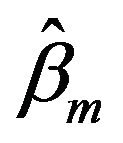 
are extreme a little, Equation (3.1) can be written as
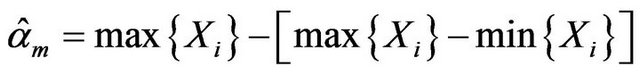
Since
is a modify to
, and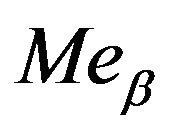 
is a modify to 
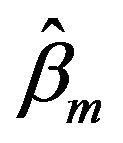too.
It can be shown that:
Theorem 4. The fiducial expect estimators of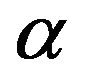 
and 
are given by
(3.6)
wang#title3_4:spProof.
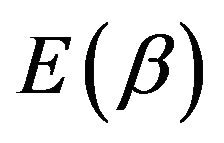can be calculated by using the same method. □
is a better modify to
, and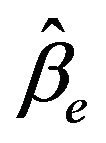 
is a better modify to 
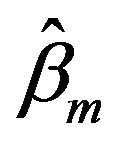as well. We suggest using 
and
.
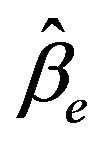The fiducial probability that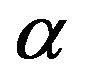 
belongs to a certain interval estimator 
can be calculated using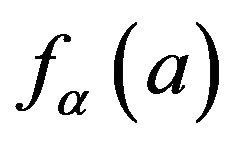 
as follows
(3.7)
In the same way
(3.8)
Give a fiducial probability 
let us consider the 
fiducial interval problem. In order to set the length of the interval as shorter as possible, we choice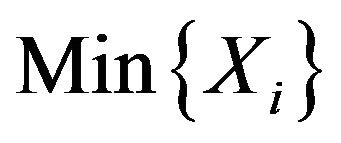 
as the right end point of the fiducial interval of
, because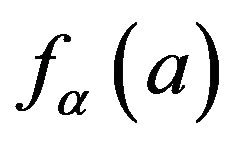 
increases; and choice 
as the left end point of the fiducial interval of
, because 
decreases.
Theorem 5. The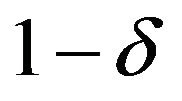 
fiducial interval of 
is
(3.9)
The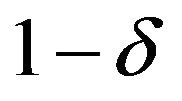 
fiducial interval of 
is
(3.10)
Proof. Denote that
Using (3.7) it can be derived that
And the bellow equation can be got by using (3.8)
□
Let us consider the 
fiducial region of
. In order to set the area of the region as smaller as possible, we choice the region as the following rectangular triangle:
(3.11)
for a certain d > 0, because 
choice the same value when 
equals to a constant, and 
increases in a when b is invariant, decreases in b when a is invariant.
Theorem 6. The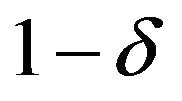 
fiducial region of 
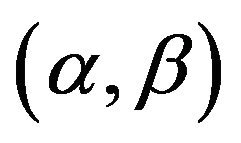is given by (3.11) if positive d satisfies
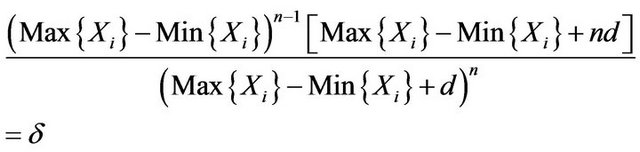(3.12)
Proof. At first Equation (3.12) has a positive solution d because its left side equal to 1 when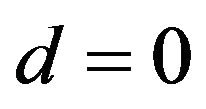 
and tends to 0 when d tends to
. Hence the fiducial probability that 
belongs to the region given by (3.11) is
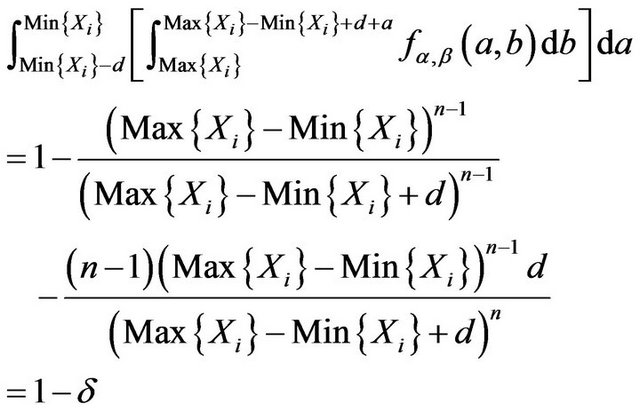
Equation (3.12) is used here. □
4. The Case That One Parameter Is in Variation
Let us consider the case that only one parameter is in variation.
is a distribution with single-parameter when one end point of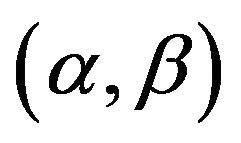 
is constant. For constant b0
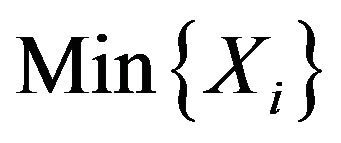is sufficient for
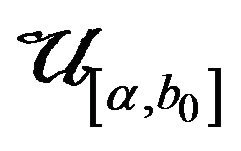. It can be got that the fiducial density of parameter 
in 
is
(4.1)
It should noted that using (2.4) and (2.6) the conditional density of 
under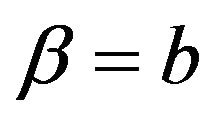 
can be got as
(4.2)
Comparing (4.1) and (4.2) is to say that (4.1) is coincided with the conditional density of 
under 
The maximum fiducial estimators, the fiducial median estimators and the fiducial expect estimators of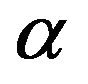 
can be got easily by using (4.1).
The fiducial probability of one interval estimator 
for 
can be calculated as
(4.3)
The 
fiducial interval of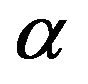 
can be got as follows by using (4.3).
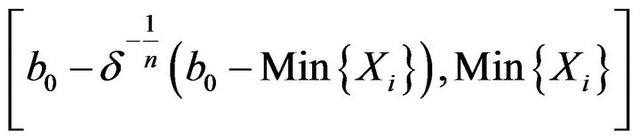(4.4)
The similar results for 
can be got easily as well.
If there is a relation between the parameters, such as the example in Section 1, this situation may be thought as missing parameter(s). We insist that the conditional distribution should be used in this situation. Under the condition that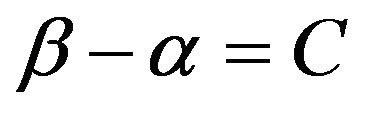 
for a constant C, the conditional density
, or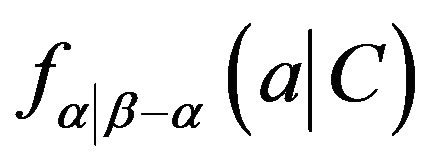
, is a constant in the interval on which its value isn’t zero, because 
is a constant when
. Since
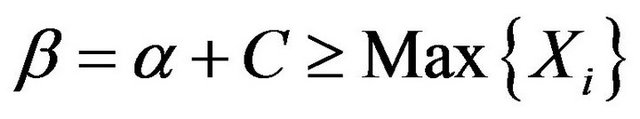the conditional density 
is the density of
. This is the fiducial density of the parameter 
of a totality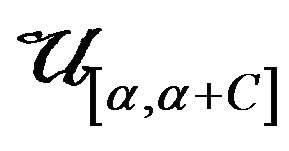
.
It can be seen that for distribution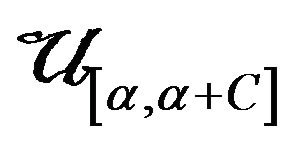
,
is a 100% fiducial interval of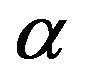
. Any subinterval of
is a 
fiducial interval of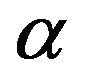 
in this problem only if it has the length
.
Using the above results to the example in Section 1 it can be got that any subinterval of [0.89, 1.08] with the length 0.95 × 0.19 is the 95% fiducial interval of
. Its length 0.1805 is much smaller than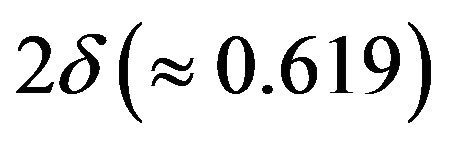
, the length of interval (*).
5. Hypothesis Testing
Let us consider the hypothesis testing problem. Equation (3.7) and (3.8) can be used to calculate the fiducial probability when the parameter would belong to the range that a certain hypothesis is true.
Theorem 7. For hypothesis
(5.1)
And should rejected H1 w.p.1 if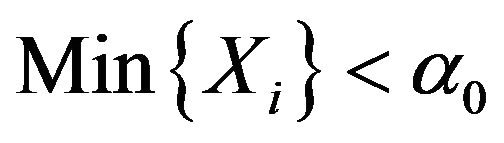
.
Proof. Choice 
and 
in (3.7). □
If for a certain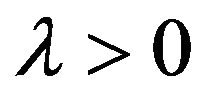
, the decision is made by comparing 
with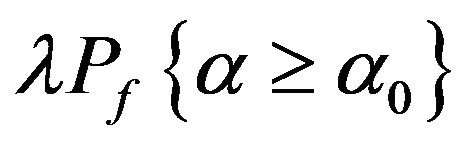
, then the criterion is that reject H0 when
(5.2)
Note that the left hand of (5.2) is the quantile of order
of the fiducial distribution of
. Especially for
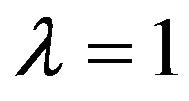the criterion is reject H0 when
(5.3)
Theorem 8. For hypothesis
The fiducial probability
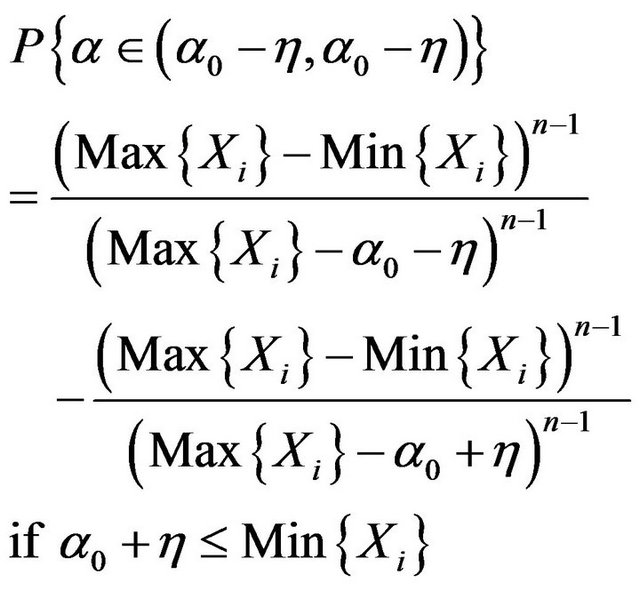
Proof. The result can be got just like theorem 7. □
The parallel results for 
can be got by using the same method as well.
Theorem 9. Hypothesis
The fiducial probability
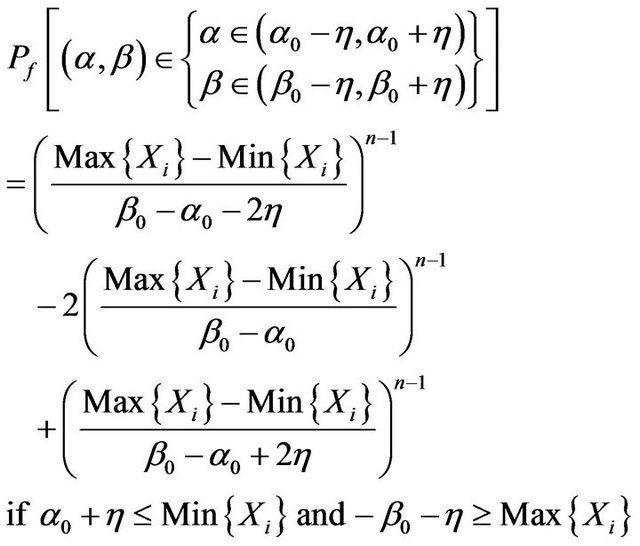
wang#title3_4:spProof.
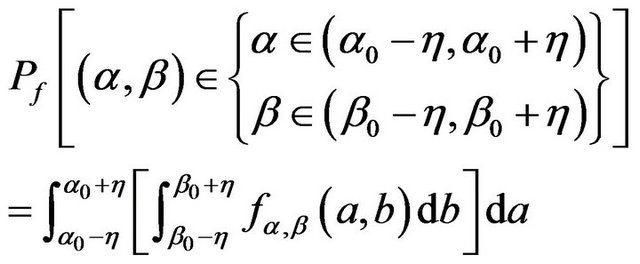
This theorem can be got by calculating the above integral. □
The fiducial probability in the situation that the parameters would belong to the range that a certain hypothesis in Theorem 7 or 8 is true can be easily got by using (4.3) in the case that one parameter is in variation.
Example. For the example in Section 1, consider the hypothesis
It can be shown that
If for a certain
, the decision is made by comparing 
with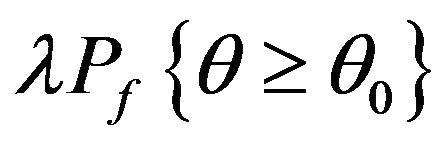
, when the one in front is greater,
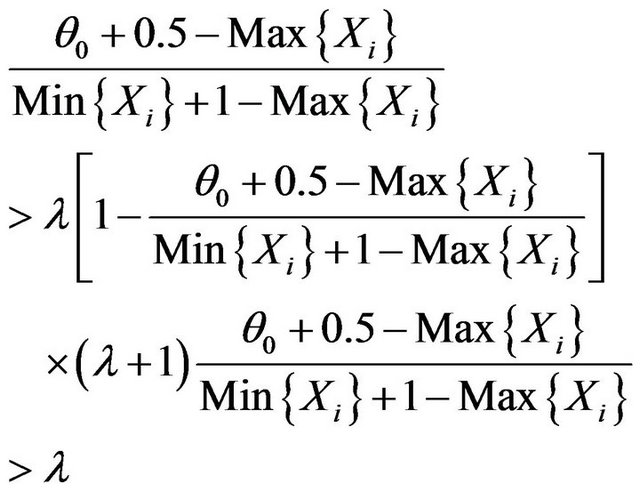
So the criterion is that reject H0 when
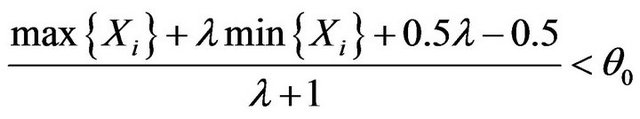(5.4)
Please note that the left hand of (5.4) is the quantile of order 
of the fiducial distribution of
. Especially for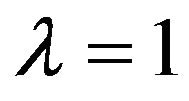 
the criterion is that reject H0 when
(5.5)
That is
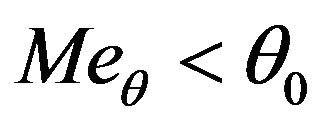(5.6)
6. Discussion
Up to now, the discussion on Fisher’s fiducial inference has still remained intuitive and imprecise. There are two problems: 1) Just what a fiducial probability means? 2) How can one derive the only fiducial distribution of the parameter(s)? Paper [4] considered the 1st problem. For the 2nd problem we guess that two sufficient statistics of least dimension, whose dimension is coincides with the parameter(s), must derive the same fiducial distribution of the parameter(s). And we insist that the marginal distribution should be used in the situation when there is (are) nuisance parameter(s); and that the conditional distribution should be used in the situation when there is (are) (a) relation(s) between the parameters.