BLU Factorization for Block Tridiagonal Matrices and Its Error Analysis ()
1. Introduction
Tridiagonal matrices are connected with different areas of science and engineering, including telecommunication system analysis [1] and finite difference methods for solving partial differential equations [2-4].
The backward error analysis is one of the most powerful tools for studying the accuracy and stability of numerical algorithms. A backward analysis for the LU factorization and for the solution of the associated triangular linear systems is presented by Amodio and Mazzia [5]. BLU factorization appears to have first been proposed for block tridiagonal matrices, which frequently arise in the discretization of partial differential equations. References relevant to this application include Isaacson and Keller [6], Bank and Rose [7], Mattheij [8], Concus, Golub and Meurant [9], Varah [10], Bank and Rose [11], and Yalamov and Plavlov [12]. For a block dense matrix, Demmel and Higham [13] presented error analysis of BLU factorization, and Demmel, Higham and Shreiber [14] also extended earlier analysis.
This paper is organized as follows. We begin, in section 2 by showing the representation of BLU factorization for block tridiagonal matrices. In section 3 some properties on the factors associated with the factorization are presented. Finally, by the use of BLAS3 based on fast matrix multiplication techniques, an error analysis of the factorization is given in section 4.
Throughout, we use the “standard model” of floatingpoint arithmetic in which the evaluation of an expression in floating-point arithmetic is denoted by , with
, with

(see Higham [15] for details). Here  is the unit rounding-off associated with the particular machine being used. Unless otherwise stated, in this section an unsubscripted norm denotes
is the unit rounding-off associated with the particular machine being used. Unless otherwise stated, in this section an unsubscripted norm denotes .
.
2. Representation of BLU Factorization for Block Tridiagonal Matrices
Consider a nonsingular block tridiagonal matrix
 , (1)
, (1)
where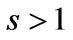 ,
,  are nonsingular,
are nonsingular,
 and
and  with
with  and
and
 are arbitrary. We present the following factorization of
are arbitrary. We present the following factorization of . The first step is represented as follows:
. The first step is represented as follows:

where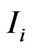 is the identity matrix of order
is the identity matrix of order , and
, and

The second step of the factorization is applied to  in order to obtain a matrix
in order to obtain a matrix  with a sub-block
with a sub-block , then
, then

Applying the method recursively, it follows that

After  steps the block
steps the block  is
is  and the factorization ends, we obtain
and the factorization ends, we obtain
 where
where  and
and . From the process of the representation obtained, we get the results as follows:
. From the process of the representation obtained, we get the results as follows:
1) Taking the second step for example, if 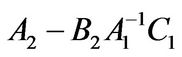 is nonsingular then we can factor
is nonsingular then we can factor  and
and 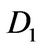 in a similar manner, and this process can be continued recursively to obtain the complete block LU factorization;
in a similar manner, and this process can be continued recursively to obtain the complete block LU factorization;
2) There exists obvious difference between partitioned LU factorization (see [15] for further details), GE and block LU factorization in this paper.
3. Some Properties on the Factors of BLU Factorization
The usual property on Schur complements under BLU factorization for block diagonal dominance by rows is similar to that of point diagonal dominance, i.e., Schur complements under BLU factorization for block diagonal dominance by rows inherit the key property on original matrices. For the factors ,
, 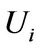 and
and , we have the following theorem.
, we have the following theorem.
Theorem 3.1. Let  in (1) be nonsingular and block diagonally dominant by rows (columns). Then the factors
in (1) be nonsingular and block diagonally dominant by rows (columns). Then the factors ,
, 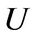 and
and also preserve the similar property.
also preserve the similar property.
Proof. By the process of the factorization, it follows that
 .
.
Since  is block diagonally dominant, by the definition of block diagonal dominance,
is block diagonally dominant, by the definition of block diagonal dominance,  preserves the same property as the matrix
preserves the same property as the matrix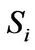 . The proof for
. The proof for 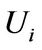 and
and  is as follows. The definition of block diagonal dominance, we have
is as follows. The definition of block diagonal dominance, we have

Thus the matrices 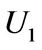 and
and  are also block diagonally dominant. The result follows by induction, that is,
are also block diagonally dominant. The result follows by induction, that is, 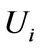 also preserves the same property as the matrix
also preserves the same property as the matrix . For the matrix U, we have
. For the matrix U, we have

By the above proof, it follows that the matrix  is also block diagonally dominant. □
is also block diagonally dominant. □
The problem is whether the matrices  for all
for all  and
and  can inherit the same property as the matrix
can inherit the same property as the matrix . The result is negative. Take the following block tridiagonal matrix and
. The result is negative. Take the following block tridiagonal matrix and  for example,
for example,
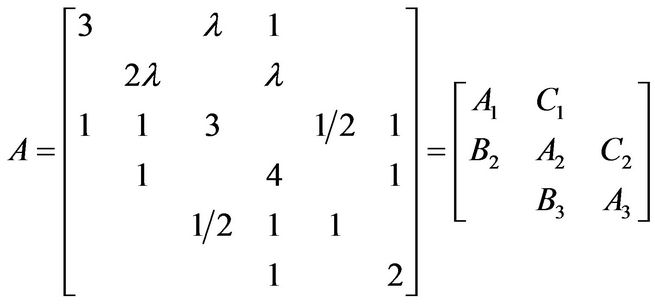 where
where 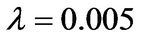 and
and ,
,  and
and  are
are  matrices. Since the following inequalities
matrices. Since the following inequalities

then the matrix 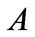 is block diagonally dominant by rows. Thus the matrix
is block diagonally dominant by rows. Thus the matrix  is also block diagonally dominant by rows. However,
is also block diagonally dominant by rows. However,
 thus
thus  and
and  are not block diagonally dominant by rows. □
are not block diagonally dominant by rows. □
Only if the matrix 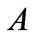 in (1) is block diagonally dominant by columns, the matrices
in (1) is block diagonally dominant by columns, the matrices  for all
for all  and
and  can preserve the key property of
can preserve the key property of . The reason is as follows.
. The reason is as follows.
Based on the definition of block diagonal dominance by columns and the key property of , we have
, we have

Therefore the matrices  and
and  are also block diagonally dominant by columns. Similarly,
are also block diagonally dominant by columns. Similarly,  for all
for all  block diagonally dominant by columns by induction. Then
block diagonally dominant by columns by induction. Then 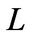 can also preserve the key property of
can also preserve the key property of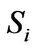 .
.
4. Error Analysis
The use of BLAS3 based on fast matrix multiplication techniques affects the stability only insofar as it increases the constant terms in the normwise backward error bounds [13]. We make assumption about the underlying level-3 BLAS (matrix-matrix operations).
If  and
and  then the computed approximation
then the computed approximation  to
to 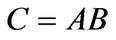 satisfies
satisfies
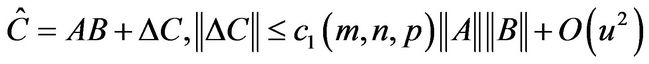 , (2)
, (2)
where  denotes a constant depending on
denotes a constant depending on  and
and . For conventional BLAS3 implementations, (2) holds with
. For conventional BLAS3 implementations, (2) holds with 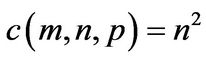 [13,15].
[13,15].
The computed solution  to the triangular systems
to the triangular systems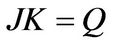 , with
, with  and
and , satisfies
, satisfies
 where
where  denotes a constant depending on
denotes a constant depending on  and
and . In this section, we present the backward error analysis for the block LU factorization by applying BLAS3 based on fast matrix multiplication techniques.
. In this section, we present the backward error analysis for the block LU factorization by applying BLAS3 based on fast matrix multiplication techniques.
Theorem 4.1. Let 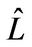 and
and 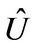 be the computed BLU factors of
be the computed BLU factors of  in (1). Then
in (1). Then

where


Proof. Applying the standard analysis of errors, we can obtain the above result. Thus we omit it. □
Let and
and . The multiplications
. The multiplications  and
and  do not produce errors because of their structures. Thus the errors of
do not produce errors because of their structures. Thus the errors of  and
and 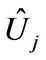 can be represented as
can be represented as  and
and  . Then
. Then

where  and
and  are the maximum values of
are the maximum values of
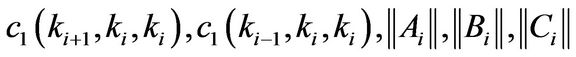 ,
,  and
and
 , respectively, when the value
, respectively, when the value  ranges from
ranges from 
to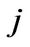 . Although the above error bounds are similar to those of
. Although the above error bounds are similar to those of  and
and ,
,  in the bounds for
in the bounds for  and
and  satisfies
satisfies . On the other hand, based on the structure
. On the other hand, based on the structure , the error bounds for
, the error bounds for  and
and  is different from those of Theorem 4.1 and we can also obtain the bound for
is different from those of Theorem 4.1 and we can also obtain the bound for .
.
Since the factors  arising in the factorization in this paper are triangular matrices, from (2) we have
arising in the factorization in this paper are triangular matrices, from (2) we have

where . Note that the multiplication
. Note that the multiplication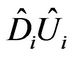 do not produce error because of the structure of
do not produce error because of the structure of  and
and . Then
. Then

Thus
 where
where  and
and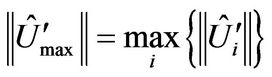 .
.
Compared to the proof of standard analysis of errors, there is a great different in form and the simpler proof of the latter embodies whose superiority. For the former, the error bound does not include , which makes the computation easier.
, which makes the computation easier.
Applying the result of Theorem 4.1, we have the following theorem.
Theorem 4.2. Let  and
and  be the computed BLU factors of
be the computed BLU factors of  in (1). Then
in (1). Then

where

Proof. To save clutter we will omit “ ” from each bound. For the expression
” from each bound. For the expression  arising in
arising in , if
, if  is sufficiently small, the term
is sufficiently small, the term  is small with respect to the other error matrices, in first order approximation, we obtain
is small with respect to the other error matrices, in first order approximation, we obtain

where

Similarly, we have

Therefore the result holds. □
From Theorems 4.1 and 4.2, the bounds for  and
and  just depend on one of factors
just depend on one of factors  and
and  of elements
of elements , which make the computation of error bounds simpler.
, which make the computation of error bounds simpler.
5. Acknowledgements
The authors would like to thank the committee of CET 2011 Conference very much for their help. Moreover, this research was supported by Guangdong NSF (32212070) and the Fundamental Research Funds for the Central Universities (12KYFC007).