1. Introduction
Decision making problems in decentralized organizations are often modeled as Stackelberg games, and they are formulated as two-level mathematical programming problems. In the Stackelberg game model, the decision maker at the upper level first specifies a strategy, and then the decision maker at the lower level specifies a strategy so as to optimize the objective with full knowledge of the action of the decision maker at the upper level [1]. Assuming that the decision maker at the lower level behaves rationally, that is, optimally responds to the decision of the decision maker at the upper level, the decision maker at the upper level also specifies the strategy so as to optimize the objective of self. Although a situation described as the above is called a Stackelberg equilibrium in the field of game theory or economics, in this paper dealing with mathematical programming, we will refer to it as a Stackelberg solution.
Even if the objective functions of both decision makers and the common constraint functions are linear, such a two-level linear programming problem is a non-convex programming problem with a special structure, and it is shown to be NP-hard [2,3]. Various computational methods for solving a two-level linear programming problem have been developed [4-10], and some real-world applications are reported [11-14].
In this paper, we deal with a purchase problem for food retailing, and formulate a two-level linear programming problem with a food retailer and a distributer under a noncooperative decision making environment. We compute the Stackelberg solution to the two-level linear programming problem, and perform sensitivity analysis from the viewpoints of the food retailer and the distributer.
Many people in Japan buy vegetables and fruits in food supermarkets, and the food supermarkets usually purchase such fresh produce from distributers who obtain them in central wholesale markets. In Japan, 80% of vegetables and 60% of fruits are distributed by way of wholesale markets [15], and this fact means that the wholesale markets have been fulfilling as an efficient intermediary role connecting consumers and farm producers.
Because Japanese consumers tend to buy small amounts of vegetables and fruits frequently, food retailers such as supermarkets must provide a wide range of fresh products every day. To cope with Japanese consumers’ behavior, in most situations, food retailers do not buy vegetables and fruits in wholesale markets or directly from farm producers but contract with distributers to purchase them. This method of purchasing decreases the transaction cost and enables distributers to supply a wider range of fresh products for customers in a timely manner [16].
To take into account the mutual interdependence of a food retailer and a distributer, we formulate a decision problem on the purchase of food for retailing as a twolevel linear programming problem with self-interested decision makers where the profits of the food retailer and the distributer are maximized. In this problem, the food retailer first specifies the order quantities of vegetables and fruits, and after receiving the order from the food retailer, the distributer determines purchase volumes of them at each of the central wholesale markets in several major cities in Japan. Although the food retailer and the distributer in this application are hypothetical decision makers, data used in the mathematical modeling are realistic.
The rest of the paper is organized as follows. In Section 2, we review the literature on food retailing and discuss the relevance of this research. In Section 3, we determine objective functions and reveal constraints of the problem, and formulate the purchase problem of the food retailer contracting with the distributer as a two-level linear programming problem. In Section 4, after gathering realistic data of the wholesale prices of the fresh produce and transportation costs, we compute the Stackelberg solution to the formulated two-level linear programming problem by using the Kth best method by Bialas and Karwan [7] and the Hansen, Jaumard and Savard method [8]. Section 5 provides sensitivity analysis from the viewpoints of the food retailer and the distributer. In Section 6, we discuss an extension of the two-level purchase problem in order to develop multi-store operations in multiple regions in Japan. Finally, to conclude this paper, we make some remarks.
2. Related Works
Recent topics on food retailers and markets are summarized as follows. Geuens et al. [17] examine the consumer perception of the current grocery shopping and the future grocery shopping alternative preferred by consumers. They show that consumers are not fond of the way they do grocery shopping at the moment, and consumers seem to prefer that retail stores evolve in retailing superstores.
To facilitate the generation of a chronological and historical explication of sustainable competitive advantage within the UK food retailing sector, Harris and Ogbonna [18] review and critically analyze the internal and external sources of competitive advantage exploited by the major UK food retailers. By presenting results from an approach which uses multiple performance measures for supermarket operations, Park and King [19] examine the impacts of information technology on business operations and industry structure in the food retailing sector and also on store level efficiency, using the data form the 2002 Supermarket Panel conducted by the Food Industry Center at the University of Minnesota. Hibara [20] takes up Ito-Yokado Group as one of leading Japanese retailers and analyze the Ito-Yokado Group’s general management strategies and its recent strategies on using information technology to achieve long-term sustainable advantage. As for a market overview in Japanese retail food sector, it is pointed out that food and beverage consumer purchases are migrating toward larger supermarkets featuring a wider assortment of merchandise at lower prices, and also toward convenience store locations, with their [21].
Next, we review some researches about planning and evaluation for food retailing. Ahumada and Villalobos [22] review the research results in the field of production and distribution planning for agri-foods based on agricultural crops, classifying the successfully implemented models according to their relevant features such as the optimization approaches used, the type of crops modeled, and so forth. Erkoc et al. [23] deal with multi-stage replenishment of an onboard food and beverage item for a cruise liner, and investigate optimal contracting and inventory replenishment policies. To model and analyze strategic issues for food supply chains, Georgiadis et al. [24] adopt the system dynamics methodology and give guidelines for the methodology. They demonstrate the applicability of the developed methodology on a multiechelon network of a major Greek fast food chain. For a real life inventory-distribution problem in food supply networks in East Asia, Lin and Chen [25] propose a hedge-based coordinated inventory replenishment and shipment methodology.
Increased competition from alternative retail formats brings significant changes into the retail food industry. Motivated by recognizing the changes, Davis et al. [26] examine the labor market adjustment of firms in response to competitive entry by using a large-scale longitudinal employer-employee matched data set. By applying the analytic hierarchy process (AHP), Erol et al. [27] propose indicators for future evaluation of industrial sustainability performance for grocery retailing in terms of the social, environmental and economic sustainability aspects. Tamura [28] studies the purchase behavior in Japan, Korea and Taiwan.
As we mentioned above, consumers in Japanese food retailing prefer purchasing in larger food supermarkets with a wide variety of vegetables and fruits, and then these facts of the markets are consist with our formulation given in the subsequent sections.
3. Problem Formulation
The food retailer deals with n kinds of vegetables and fruits which are purchased from the distributer. The distributer buys vegetables and fruits ordered from the food retailer at the central wholesale markets in s cities, and transports them by truck from each of the central wholesaler markets to the food retailer’s storehouse in Tokyo. The two decision makers make an agreement that the distributer has an obligation to transport the foods to the storehouse, but the cost of the transportation is paid by the food retailer.
Let  denote an order quantity of food i specified by the food retailer to the distributer, and let
denote an order quantity of food i specified by the food retailer to the distributer, and let  denote a purchase volume of food i at the central wholesale market in city j. For concise representation, on occasion the decision variables are expressed by
denote a purchase volume of food i at the central wholesale market in city j. For concise representation, on occasion the decision variables are expressed by 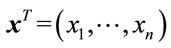 and
and  .
.
Objective functions: The profit of the food retailer is represented by
 (1)
(1)
where ai is the margin per unit of food i, and bji is the transportation cost per unit of food i from city j.
The profit of the distributer is represented by
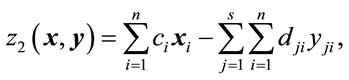 (2)
(2)
where ci is the selling price of food i to the food retailer, and dji is the purchase price of food i at the central wholesale market in city j.
Constraints: Let W be the capacity of the storehouse of the food retailer, and let vi be the cubic volume per unit of food i. The constraint for the storehouse is represented by
 (3)
(3)
For any food i, an order quantity of food i is specified by the food retailer between the lower limit  and the upper limit
and the upper limit , taking into account the volume of inventories. Then, the constraints for the upper and lower limits are represented by
, taking into account the volume of inventories. Then, the constraints for the upper and lower limits are represented by
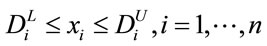 (4)
(4)
The distributer buys food i at one or more central wholesale markets, and then the total volume of food i must be larger than or equal to the quantity ordered by the food retailer. Thus, the constraints for order quantities are represented by
 (5)
(5)
Moreover, there are constraints on financial resources of the distributer for purchasing foods at the central wholesaler markets, and they are expressed by
 (6)
(6)
where oj is the budget cap in city j.
Two-level linear programming problemsAtwo-level linear programming problem for purchase in food retailing, in which the objective functions (1) and (2) are maximized under the constraints described above (3)-(6), is formulated as follows:
 (7)
(7)
4. Parameter Setting and the Stackelberg Solution
We assume that the food retailer sells 16 vegetables and fruits, i.e., n = 16, and the distributer purchases them at central wholesale markets in 8 cities, i.e., s = 8. The retail and the purchase prices of the food retailer’s 16 items are shown in Table 1, and the margin per unit ai of food i is the difference between the retail price and the purchase price ci. Foods  represent onions, potatoes, cabbage, Japanese radish, Chinese cabbage, carrots, cucumbers, lettuce, tomatoes, spinach, eggplant, apples, bananas, strawberries, mandarin oranges, and lemons, respectively; and cities
represent onions, potatoes, cabbage, Japanese radish, Chinese cabbage, carrots, cucumbers, lettuce, tomatoes, spinach, eggplant, apples, bananas, strawberries, mandarin oranges, and lemons, respectively; and cities  stand for Sapporo, Sendai, Niigata, Kanazawa, Tokyo, Osaka, Hiroshima, and Miyazaki, respectively. The retail prices are specified such that the cost to sales ratios range from 50% to 75%, and the average cost to sales ratios of the 16 items is about 60%. The purchase prices of the food retailer corresponding to the selling prices of the distributer are about 95% of the wholesale prices at the central wholesale market in Tokyo. The wholesale prices dji in each city are shown in Table 2, and these prices are the averages of prices in March, 2008 at the central wholesale markets.
stand for Sapporo, Sendai, Niigata, Kanazawa, Tokyo, Osaka, Hiroshima, and Miyazaki, respectively. The retail prices are specified such that the cost to sales ratios range from 50% to 75%, and the average cost to sales ratios of the 16 items is about 60%. The purchase prices of the food retailer corresponding to the selling prices of the distributer are about 95% of the wholesale prices at the central wholesale market in Tokyo. The wholesale prices dji in each city are shown in Table 2, and these prices are the averages of prices in March, 2008 at the central wholesale markets.
The fresh foods are transported from each of the 8 cities to the storehouse of the food retailer in Tokyo by truck. The transportation cost per unit bji of food i from city j to the storehouse is given in Table 3, and it is calculated under the assumption that the capacity of a truck is 8 tons, express toll highways are utilized, and the cost of fuel is ¥116 per liter. The capacity of the storehouse is 150 [m2] × 2 [m], and the cubic volumes of food i per kilogram are shown in Table 4.
The lower limit  of an order quantity of food i is determined by reference to the demand of 10,000 households, and the upper limit
of an order quantity of food i is determined by reference to the demand of 10,000 households, and the upper limit  is set from 1.1 to 1.4
is set from 1.1 to 1.4

Table 1. Retail and purchase prices of fresh food [yen/kg].


Table 2. Wholesale prices in each city [yen/kg].
times the quantities of the lower limit ; these figures are shown in Table 5. The budget caps oj on purchases in 8 cities are given in Table 6.
; these figures are shown in Table 5. The budget caps oj on purchases in 8 cities are given in Table 6.
We computed the Stackelberg solution to problem (7) with parameters shown in Tables 1-6 by using the Kth best method [7] and the Hansen, Jaumard and Savard method [8]. The solution is given in Table 7. We used a PC with Intel Pentium IV 2.80 GHz, and the computational times of the Kth best method and the Hansen, Jaumard and Savard method were 2186.296 seconds and


Table 3. Transportation costs [yen/kg].

Table 4. Cubic volumes of foods [cm3/kg].
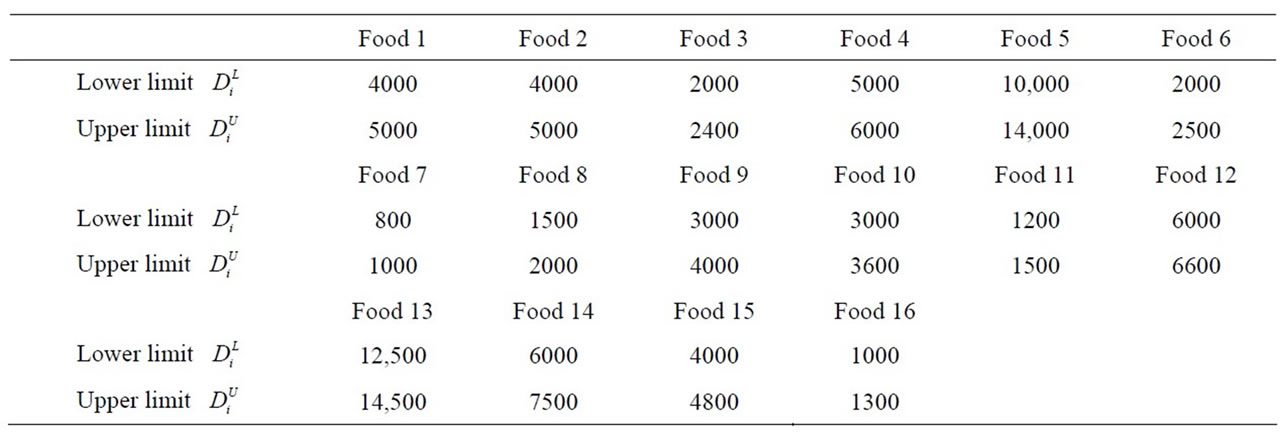
Table 5. Lower and upper limits of the foods [kg].

Table 6. Caps on purchase for eight cities [yen].

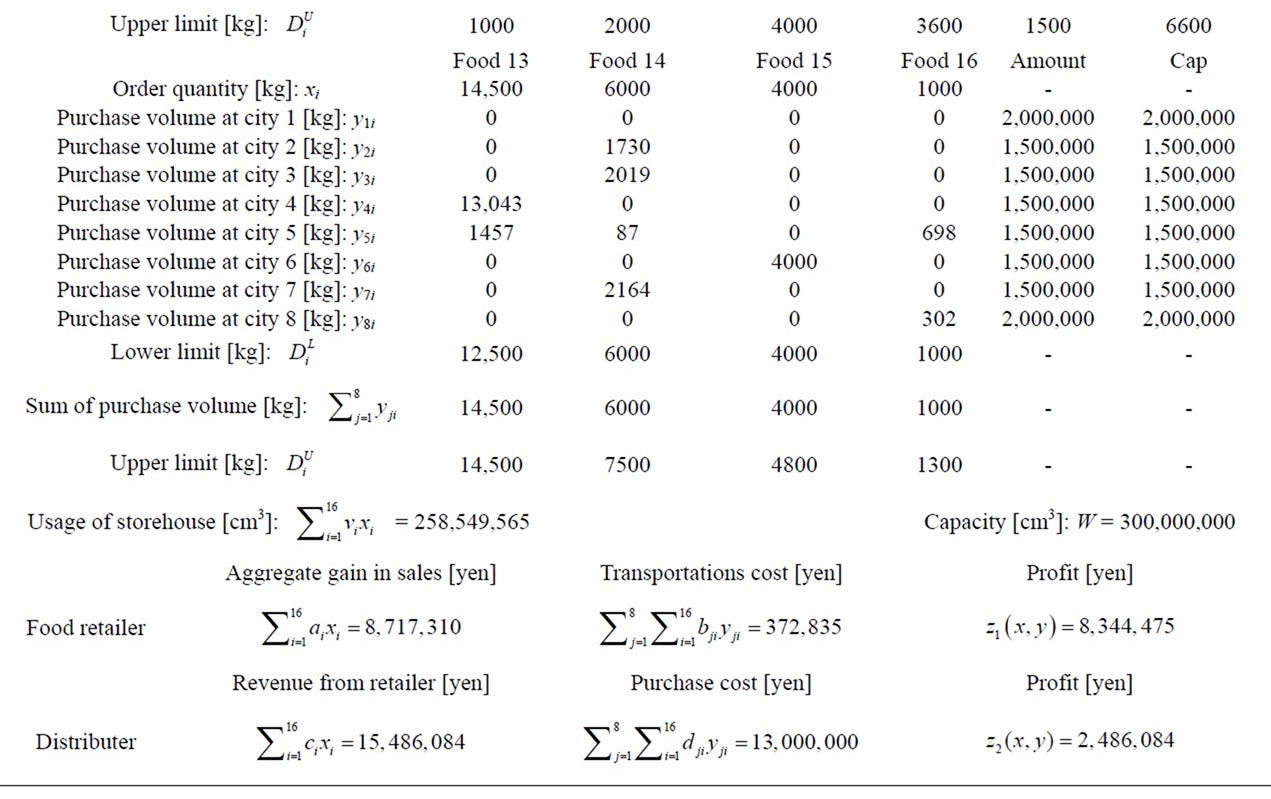
Table 7. Result of two-level purchase problem for food retailing.
5.531 seconds, respectively.
To examine the characteristics of the Stackelberg solution shown in Table 7, we give the profitability of each food for the food retailer,  , and the profit of each food per unit for the distributer,
, and the profit of each food per unit for the distributer, 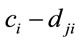 , in Tables 8 and 9, respectively. As seen in Table 7, the profits of the food retailer and the distributer are
, in Tables 8 and 9, respectively. As seen in Table 7, the profits of the food retailer and the distributer are 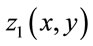 = ¥8,344,475 and
= ¥8,344,475 and  = ¥2,486,084. The order quantities of foods 3 and 13 reach the upper limit
= ¥2,486,084. The order quantities of foods 3 and 13 reach the upper limit , that of food 1 is between the upper limit
, that of food 1 is between the upper limit 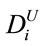 and the lower limit
and the lower limit , and those of the rest of the foods are at the lower limit
, and those of the rest of the foods are at the lower limit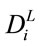 . The purchase costs in all the cities reach the budget caps. Although the wholesale prices dji of foods are greater than the selling price ci to the food retailer in city 5, Tokyo, the distributer buys foods 10, 12, 13, 14, and 16 in order to fill the order from the food retailer. Basically, as seen in Tables 7-9, the food retailer orders highly profitable foods at the upper limit, and the distributer buys high-margin foods in the corresponding cities within the budget caps. For example, food 3, cabbage, is most profitable, and then the food retailer orders food 3 up to the upper limit, 2400 units, and the distributer buys food 3 in city 8, Miyazaki, as expected.
. The purchase costs in all the cities reach the budget caps. Although the wholesale prices dji of foods are greater than the selling price ci to the food retailer in city 5, Tokyo, the distributer buys foods 10, 12, 13, 14, and 16 in order to fill the order from the food retailer. Basically, as seen in Tables 7-9, the food retailer orders highly profitable foods at the upper limit, and the distributer buys high-margin foods in the corresponding cities within the budget caps. For example, food 3, cabbage, is most profitable, and then the food retailer orders food 3 up to the upper limit, 2400 units, and the distributer buys food 3 in city 8, Miyazaki, as expected.
5. Sensitivity Analysis
First, from the viewpoint of the food retailer, we examine variations of the solutions when some parameters are changed. Changes in the cost of fuel for truck transportation are an issue of considerable concern for the management of the food retailer. Although we assume that the cost of fuel is ¥116 per liter in the previous section, we compute the Stackelberg solution for problem (7) again on the assumption that the cost of fuel is ¥150 per liter because the highest fuel price in 2008 in Japan was ¥148 per liter. In this case, the solution is the same as before, but the profit of the food retailer decreases from z1 = ¥8,344,475 to z1 = ¥8,318,173 by ¥26,302 because of the increase in the transportation costs.
Moreover, suppose that the food retailer selects the most profitable food i, and increases its upper limit  of the order quantity by 100 units. Because the most profitable food for the food retailer is food 3, cabbage, as seen in Table 8, the upper limit
of the order quantity by 100 units. Because the most profitable food for the food retailer is food 3, cabbage, as seen in Table 8, the upper limit  of food 3 is changed from 2400 to 2500 units. The Stackelberg solution to the slightly changed problem is shown in Table 10. The upper limit of
of food 3 is changed from 2400 to 2500 units. The Stackelberg solution to the slightly changed problem is shown in Table 10. The upper limit of  of food 3 is shown in a gray box, and the numbers changed from the original solution are marked with asterisks. The profit of the food retailer becomes
of food 3 is shown in a gray box, and the numbers changed from the original solution are marked with asterisks. The profit of the food retailer becomes 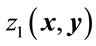 = ¥8,346,364, and it increases by about ¥2000. In contrast, the profit of the distributer is
= ¥8,346,364, and it increases by about ¥2000. In contrast, the profit of the distributer is  = ¥2,483,259, and it decreases by about ¥3000. Because the whole order quantity increases, but the distributer must buy foods in cities in which the prices are relatively higher, the profit of the distributer decreases.
= ¥2,483,259, and it decreases by about ¥3000. Because the whole order quantity increases, but the distributer must buy foods in cities in which the prices are relatively higher, the profit of the distributer decreases.

Table 8. Profitability of each food for the food retailer.
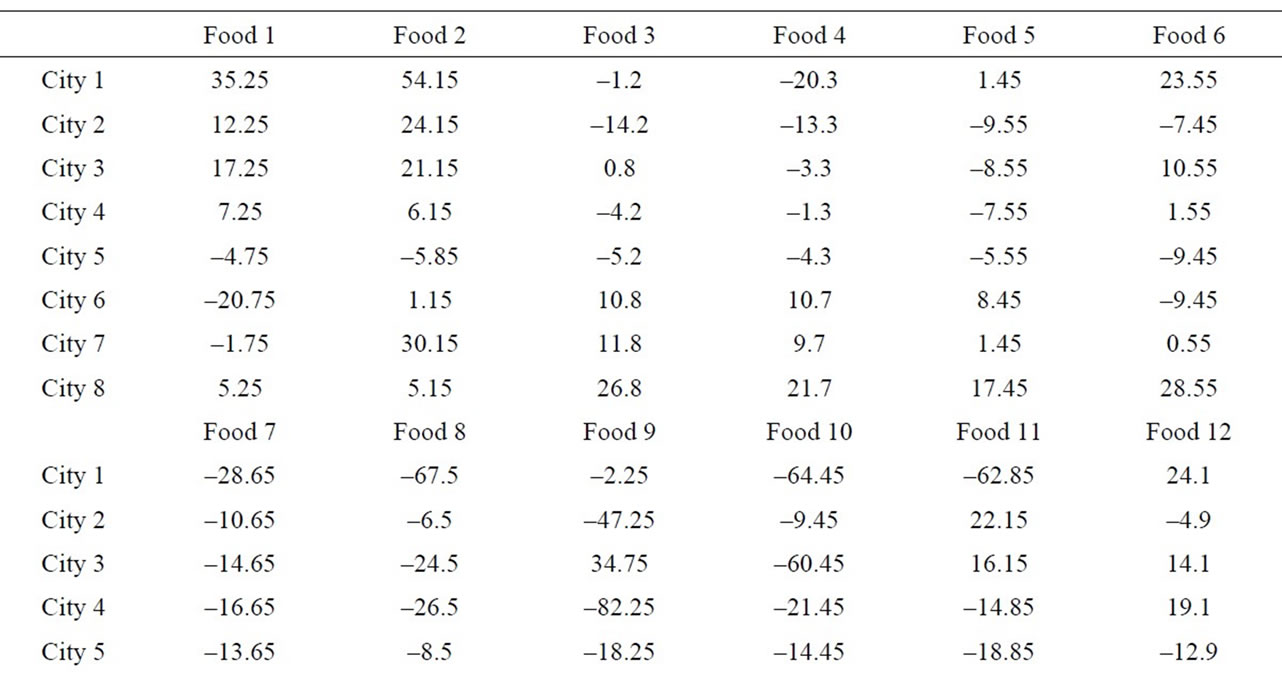

Table 9. Profit of each food per unit of the distributer.
Specifically, the expansion of the upper limit of food 3 increases the purchase volume of food 3 in city 8, decreases that of food 16 in city 8, increases that of food 16 in city 5, decreases that of food 12 in city 5, increases that of food 12 in city 1, and finally decreases that of food 1 in city 1.
Next, we conduct a sensitivity analysis from the viewpoint of the distributer. Assume that the distributer increases the budget cap of city 8, Miyazaki, where the prices of most foods are lower compared to the other districts, from ¥2,000,000 to ¥2,100,000. The Stackelberg solution to the problem with the larger budget cap is given in Table 11. The enlarged budget cap is shown in a gray box, and the numbers changed from the original solution are marked with asterisks. The profit of the food retailer becomes  = ¥8,427,859, and it increases by about ¥83,000. The profit of the distributer is
= ¥8,427,859, and it increases by about ¥83,000. The profit of the distributer is  = ¥2,549,441, and it also increases by about ¥63,000. The enlarged budget cap increases the purchase volumes of a couple of foods in city 8, and by these changes the purchase volumes of some foods in cities 1 and 5 are changed. Moreover, the order quantities of foods 1, 8, and 11 specified by the food retailer also increase, and therefore the profit of the food retailer increases.
= ¥2,549,441, and it also increases by about ¥63,000. The enlarged budget cap increases the purchase volumes of a couple of foods in city 8, and by these changes the purchase volumes of some foods in cities 1 and 5 are changed. Moreover, the order quantities of foods 1, 8, and 11 specified by the food retailer also increase, and therefore the profit of the food retailer increases.
6. Sensitivity Analysis
We discuss an extension of the two-level purchase problem to cope with a multi-store operation in multiple regions in this section. As in the single store problem, the food retailer deals with n kinds of vegetables and fruits, and it has r stores in different cities in Japan. Therefore, after buying vegetables and fruits ordered from the food retailer at the central wholesale markets in s cities, the distributer transports them by truck from each of the central wholesaler markets to the food retailer’s storehouses in r cities.
Let  denote an order quantity of food i at store k, and the decision variables of the order quantities are also expressed by vectors
denote an order quantity of food i at store k, and the decision variables of the order quantities are also expressed by vectors
 .
.

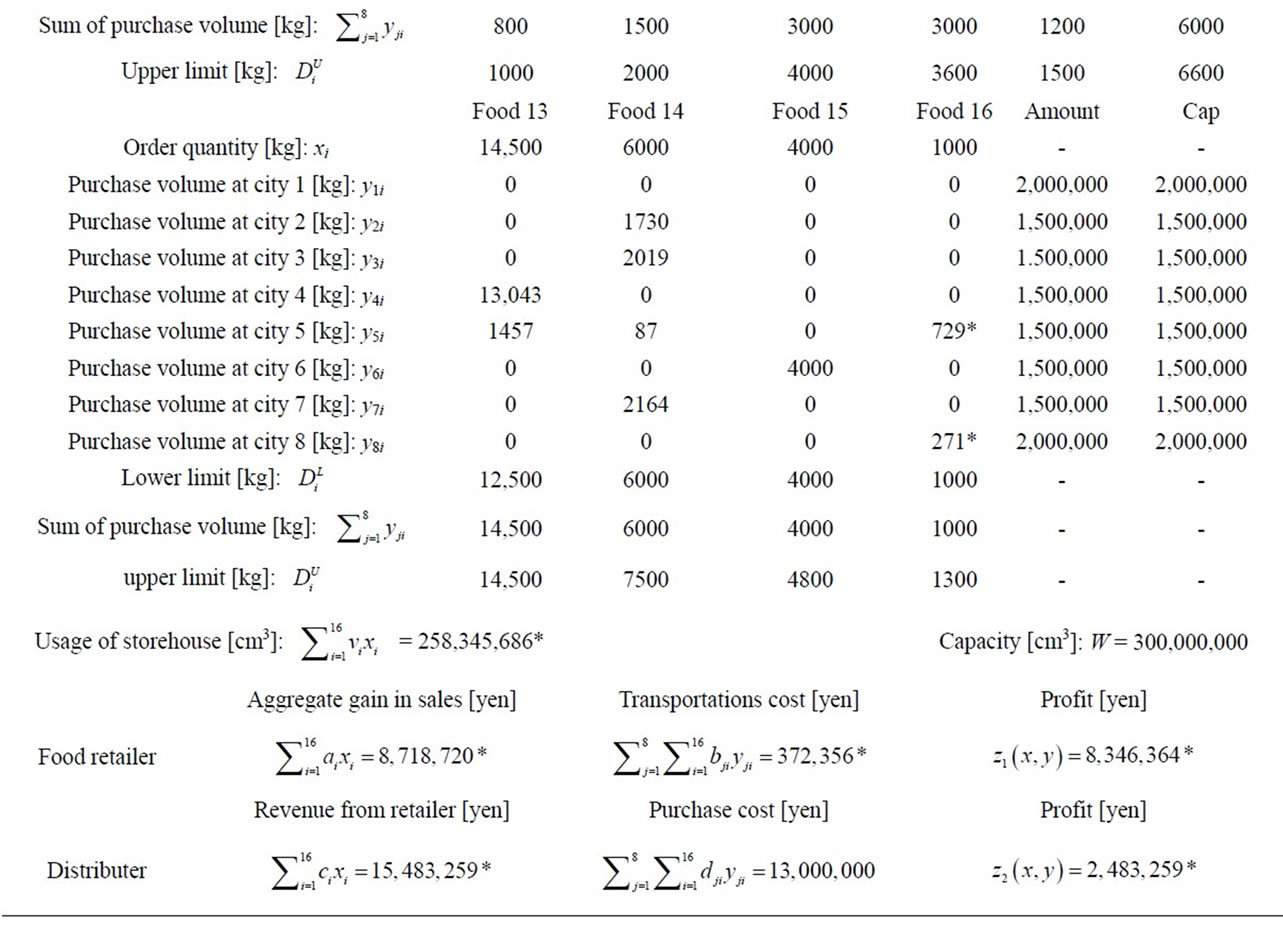
Table 10. Sensitivity analysis for the food retailer.
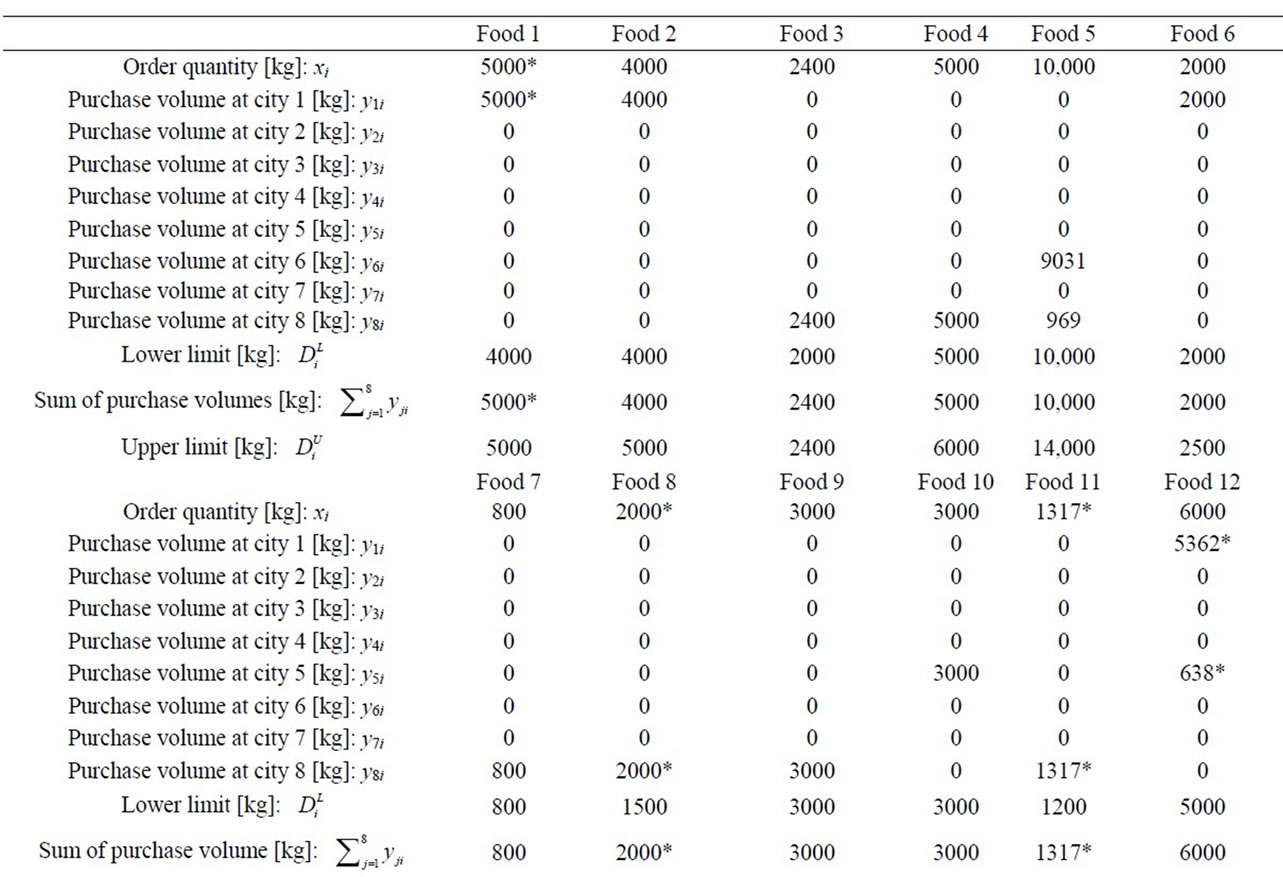
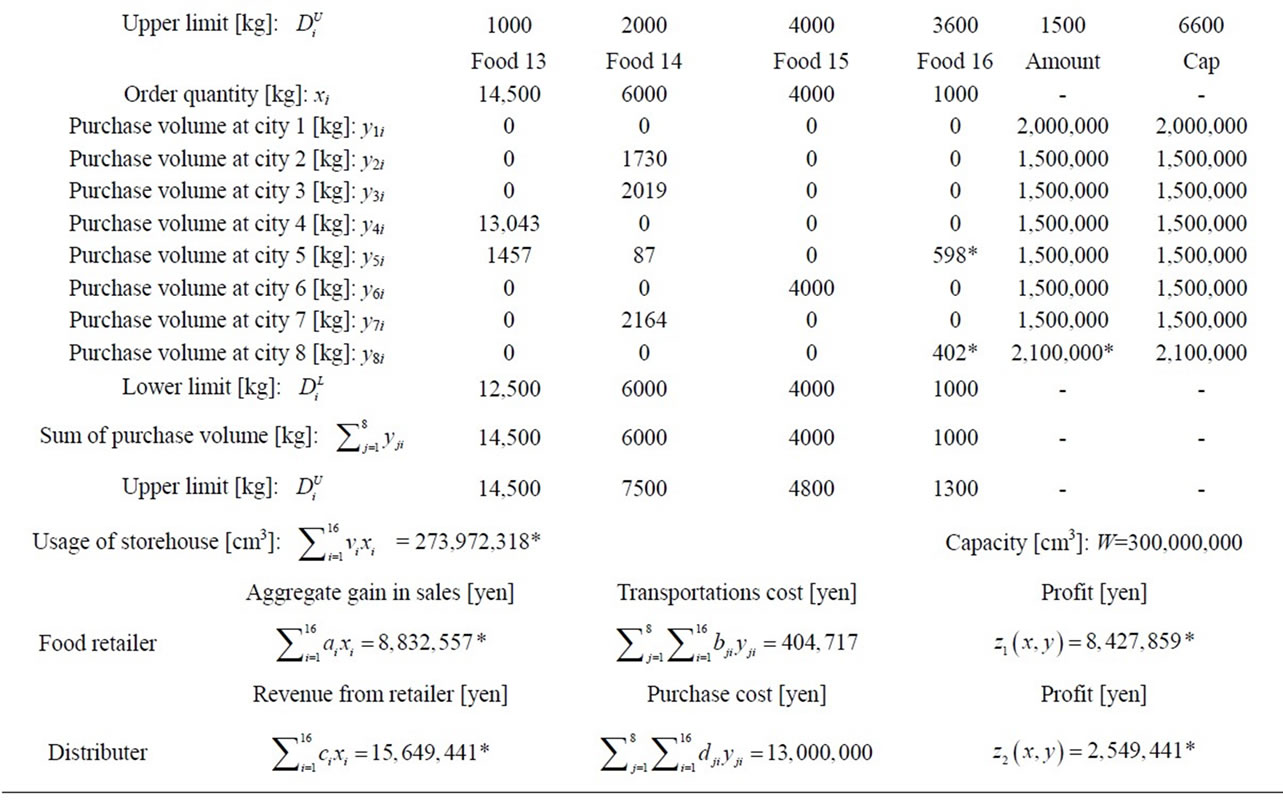
Table 11. Sensitivity analysis for the distributer.
The decision variables


of purchase volumes are the same as those of the single store problem. In the extended problem, new decision variables on transportation are introduced, and let tjki denote transportation volumes of food i from the central wholesaler market in city j to the storehouse for store k.
Let Wk denote the capacity of the storehouse of the food retailer for store . The constraints for the storehouses are represented by
. The constraints for the storehouses are represented by
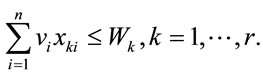 (8)
(8)
With multiple stores, the lower limits and the upper limits of order quantities of foods are also specified for all the stores, and the constraints for the upper and lower limits are represented by
 (9)
(9)
The distributer must purchase food i such that its volume is larger than or equal to the quantity ordered from the food retailer for all the stores at the central wholesaler markets in one or more cities, and then, the constraints for order quantities are represented by
 (10)
(10)
The constraints on financial resources of the distributer are the same as those (6) of the single store problem.
For the extended problem with multi-store operation, the profit of the food retailer is represented by
 (11)
(11)
where and ai is the profit per unit of food i;  and bjki is the transportation cost per unit of food i from city j to store k. The second term
and bjki is the transportation cost per unit of food i from city j to store k. The second term  of the objective function (11) is the optimal value of the following linear programming problem:
of the objective function (11) is the optimal value of the following linear programming problem:
 (12)
(12)
It follows that problem (12) is separable into the following sub-problems for food :
:
 (13)
(13)
The profit of the distributer is represented by
 (14)
(14)
where ci is the selling price of food i to the food retailer, and dji is the buying price of food i at the central wholesale market in city j.
The extended problem with a multi-store operation for purchase in food retailing is formulated as follows:
 (15)
(15)
Because the objective function (11) includes the minimization problem (12), problem (15) becomes a threelevel linear programming problem, and it can be transformed into the following single level mathematical programming problem where the Kuhn-Tucker conditions for optimality of the linear programming problems at the second and the third levels are involved in its constraints:
 (16)
(16)
where KT2 is a set of y satisfying the Kuhn-Tucker optimality condition for the second level problem (15); t is a vector of variables , and KT3 is a set of t satisfying the Kuhn-Tucker optimality condition for the third level problem (12). Although problem (15) can be solved by directly applying the Bard method [29] for three-level linear programming problems if the size of the problem is not large, as might be expected, it becomes difficult to solve it when the numbers of foods and stores are large. Because problem (16) can be transformed into a mixed zero-one programming problem, a computational method based on genetic algorithms seems to be promising as we have given the computational results on performance of the solution method for obtaining Stackelberg solutions to two-level linear programming problems.
, and KT3 is a set of t satisfying the Kuhn-Tucker optimality condition for the third level problem (12). Although problem (15) can be solved by directly applying the Bard method [29] for three-level linear programming problems if the size of the problem is not large, as might be expected, it becomes difficult to solve it when the numbers of foods and stores are large. Because problem (16) can be transformed into a mixed zero-one programming problem, a computational method based on genetic algorithms seems to be promising as we have given the computational results on performance of the solution method for obtaining Stackelberg solutions to two-level linear programming problems.
7. Conclusion
In this paper, we considered the food retailing and transportation problem, and taking into account mutual interdependence of the food retailer and the distributer, we formulated a two-level linear programming problem in a noncooperative way and computed the Stackelberg solution to the problem. Using the realistic data, we specified the parameters in mathematical modeling and closely examined the obtained solution. Moreover, from the viewpoints of the food retailer and the distributer, we performed some sensitivity analyses. Finally, we discussed the extension of the two-level linear programming problem for food retailing and transportation to cope with multi-store operation.