1. Introduction
The vulnerability of communication network measures the resistance of network to the disruption of operation after the failure of certain station or communication links. For any communication network greater degrees of stability or less vulnerability is required. Vulnerability can be measured by certain parameters like connectivity, toughness, integrity, binding number etc. In the analysis of vulnerability of communication network to disruption, following two parameters are of great importance: 1) The size of the largest remaining group within which mutual communication can still occur; 2) The number of elements that are not functioning. In this context Barefoot et al. [1] have introduced the concept of integrity of a graph as a new measure of vulnerability of network.
Definition 1.1. The integrity of a graph G is denoted by 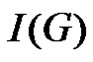 and defined by
and defined by 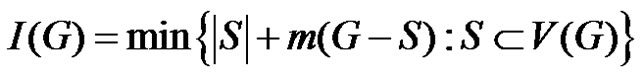 where m(G – S) is the order of a maximum component of
where m(G – S) is the order of a maximum component of 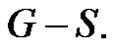
Definition 1.2. An I-set of G is any (proper) subset S of 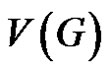 for which
for which 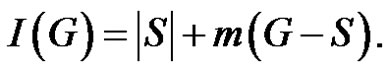
The connectedness of graph is not essential to define integrity. The integrity of middle graphs is discussed by Mamut and Vumar [2] while integrity of total graphs is discussed by Dundar and Aytac [3]. If D is any minimal dominating set and if the order of the largest component of G – D is small then the removal of D will crash the communication network. The decision making process as well as communication between remaining members will also be highly affected. Considering this aspect Sundareswaran and Swaminathan [4] introduced the concept of domination integrity which is defined as follows.
Definition 1.3. The domination integrity of a connected graph G is denoted as 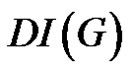 and defined by
and defined by 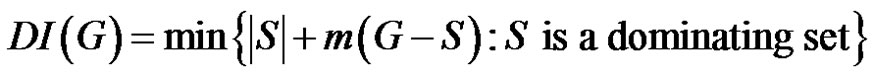 where
where 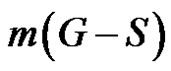 is the order of a maximum component of
is the order of a maximum component of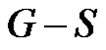 .
.
Sundareswarn and Swaminathan [5] have investigated domination integrity of middle graph of some graphs. In the present work, we investigate the domination integrity for the graphs obtained by various graph operations. In other words we have tried to relate expansion of network with measure of vulnerability.
Definition 1.4. Duplication of a vertex 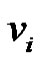 by a new edge
by a new edge 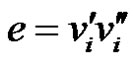 in graph G produces a new graph
in graph G produces a new graph 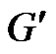 such that
such that 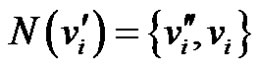 and
and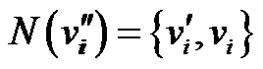 .
.
Definition 1.5. Duplication of an edge 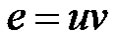 by a new vertex
by a new vertex 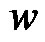 in a graph G produces a new graph
in a graph G produces a new graph 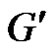 such that
such that 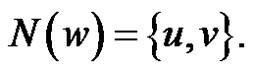
Definition 1.6. For the dominating set 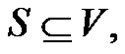 a vertex
a vertex 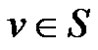 is called isolate of
is called isolate of 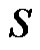 if
if 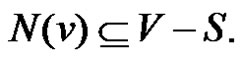
For all other standard terminology and graph theoretical notation we refer to Hynes et al. [6].
2. Main Results
Lemma 2.1. Let G be a graph obtained by duplication of each edge by vertex of path 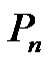 then
then 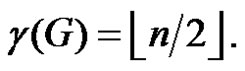
Proof: Let G be a graph obtained by duplicating each edge 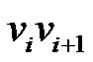 of path
of path 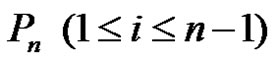 by vertex
by vertex 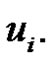 There are three types of vertices in G
There are three types of vertices in G
1) 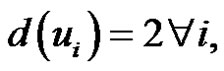
2) 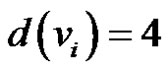 for
for 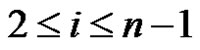 and
and
3) 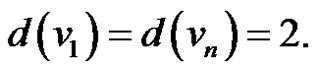
It is obvious that 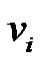 must be in the dominating set as they are the most dominating vertices. From the nature of the graph G it is obvious that out of the vertices
must be in the dominating set as they are the most dominating vertices. From the nature of the graph G it is obvious that out of the vertices 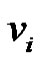 and
and 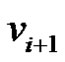 at least one vertex must belongs to any dominating set S as
at least one vertex must belongs to any dominating set S as 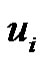 is adjacent to only
is adjacent to only 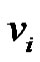 and
and 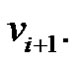 Therefore if S is any dominating set then
Therefore if S is any dominating set then 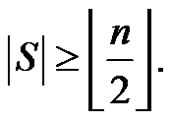
We claim that 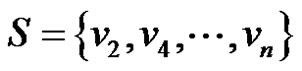 when n is even and
when n is even and 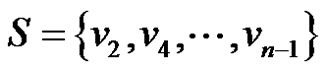 when
when 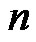 is odd are minimal dominating sets.
is odd are minimal dominating sets.
One can observe that each 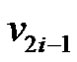 and
and 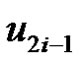 are adjacent to v2i and removal of
are adjacent to v2i and removal of 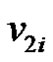 from set S,
from set S, 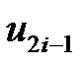 will not be dominated by any vertex of S Hence
will not be dominated by any vertex of S Hence 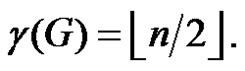
Theorem 2.2. Let G be a graph obtained by duplication of each edge by vertex of path 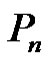 then
then
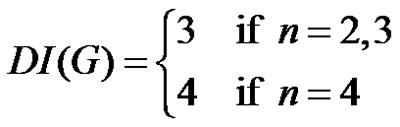
Proof: To prove the result, we consider following three cases.
Case-1. When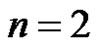 : Let G be a graph obtained by duplication of an edge
: Let G be a graph obtained by duplication of an edge 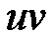 of path
of path 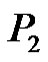 by a vertex
by a vertex 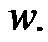 Then
Then 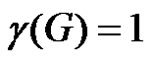 and
and 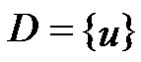 as a γ-set of G and then
as a γ-set of G and then 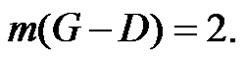 This implies
This implies 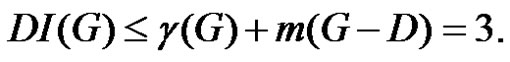 If
If 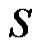 is any dominating set with
is any dominating set with 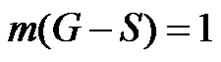 then
then 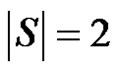 and consequently
and consequently 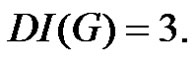 Hence in all the cases
Hence in all the cases 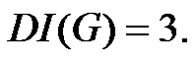
Case-2. When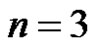 : Let G be a graph obtained by duplication of an edge v1v2 and v2v3 of path
: Let G be a graph obtained by duplication of an edge v1v2 and v2v3 of path 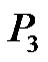 by the vertices u1 and u3 respectively. As
by the vertices u1 and u3 respectively. As 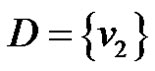 is the only γ-set of G then
is the only γ-set of G then 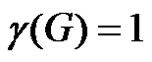 and m(G – D) = 2. If S1 is any dominating set with
and m(G – D) = 2. If S1 is any dominating set with 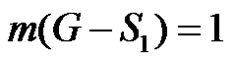 then
then 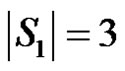 and
and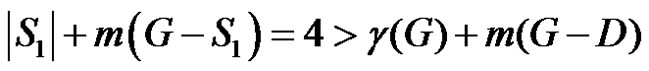 . If S2 is any dominating set with
. If S2 is any dominating set with 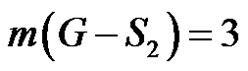 then
then 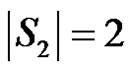 and
and 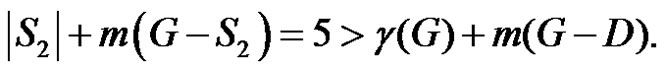 Moreover
Moreover 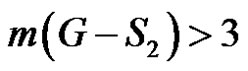 is not possible, as the order of the largest component of
is not possible, as the order of the largest component of 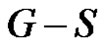 is at most 3. Thus
is at most 3. Thus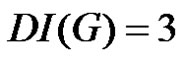 .
.
Case-3. When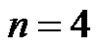 : Let G be a graph obtained by duplication of an edge
: Let G be a graph obtained by duplication of an edge 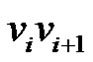 of path
of path 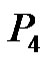 by vertex
by vertex 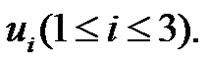 Then
Then 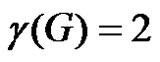 with
with 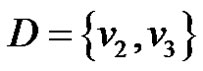 is a γ- set of
is a γ- set of 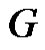 and
and 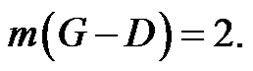 Consequently
Consequently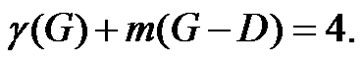 If
If 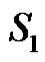 is any dominating set with
is any dominating set with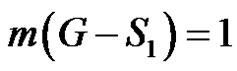 then
then 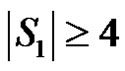 and
and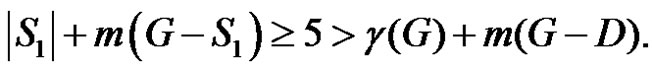 If
If 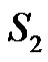 is any dominating set with
is any dominating set with 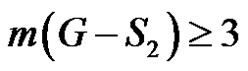 then
then 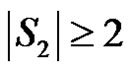 and
and 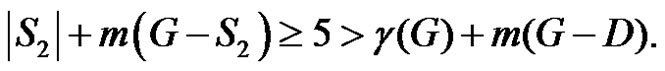 Hence we have
Hence we have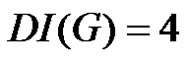 .
.
Theorem 2.3. Let 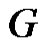 be a graph obtained by duplication of each edge by vertex of path
be a graph obtained by duplication of each edge by vertex of path 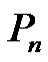 then
then
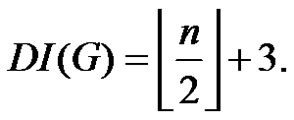 (if
(if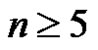 )
)
Proof: Let G be a graph obtained by duplicating each edge vivi+1 of path Pn by vertex 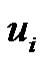 where
where 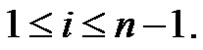
Then from Theorem 2.1 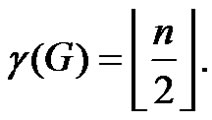 If n is even then
If n is even then 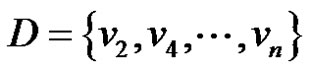 is a γ-set of G otherwise
is a γ-set of G otherwise 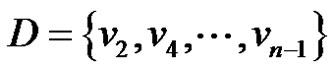 is a γ-set of G Therefore
is a γ-set of G Therefore 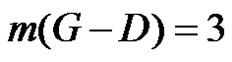 which implies,
which implies,
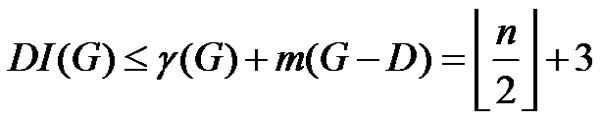 (1)
(1)
We will show that the number 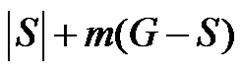 is minimum. For that we have to take into account the minimality of both
is minimum. For that we have to take into account the minimality of both 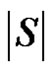 and
and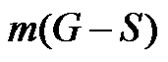 . The minimality of
. The minimality of 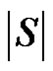 is guaranteed as S is γ-set. Now it remains to show that if S is any dominating set other than D then
is guaranteed as S is γ-set. Now it remains to show that if S is any dominating set other than D then 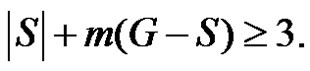
If 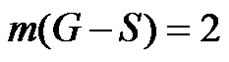 then
then 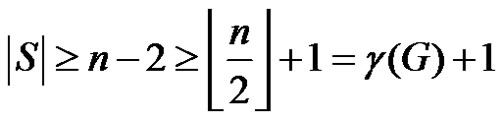
and 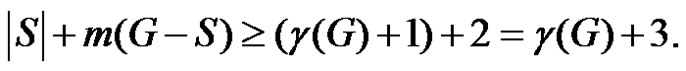
If 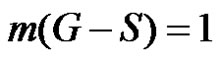 then
then 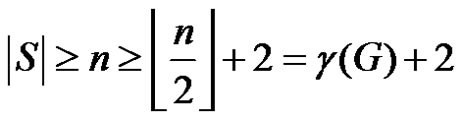
which implies that
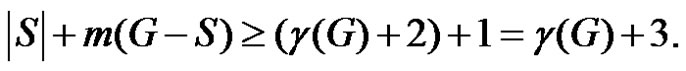
If 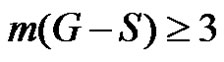 then trivially
then trivially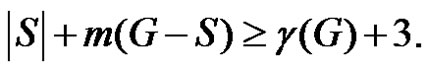 Hence for any dominating set S
Hence for any dominating set S
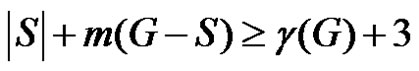 (2)
(2)
From (1) and (2) we have 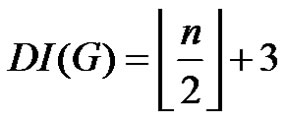 (if n ≥ 5).
(if n ≥ 5).
Theorem 2.4. Let 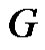 be a graph obtained by duplication of each vertex by an edge of path
be a graph obtained by duplication of each vertex by an edge of path 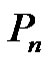 or cycle
or cycle 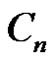 then
then 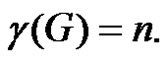
Proof: Let 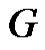 be a graph obtained by duplication of vertices
be a graph obtained by duplication of vertices 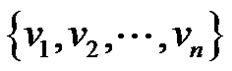 of path
of path 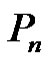 or cycle
or cycle 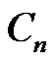 by an edge
by an edge 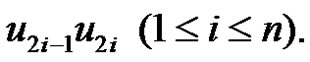 Then from the construction of graph G it is obvious that from the vertices
Then from the construction of graph G it is obvious that from the vertices 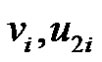 and
and 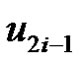 at least one vertex must belong to any dominating set
at least one vertex must belong to any dominating set 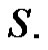 Consequently if
Consequently if 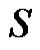 is any dominating set then
is any dominating set then 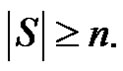
We claim that set 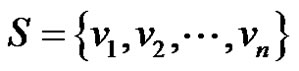 is a minimal dominating set. Because each
is a minimal dominating set. Because each 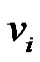 is adjacent to
is adjacent to 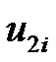 and
and 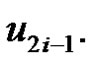 If
If 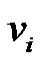 is removed from set
is removed from set 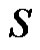 then
then 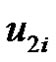 and
and 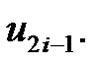 will not be dominated by any vertex. Thus
will not be dominated by any vertex. Thus 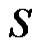 is a minimal dominating set with minimum cardinality. Hence
is a minimal dominating set with minimum cardinality. Hence 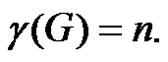
Theorem 2.5. Let 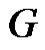 be a graph obtained by duplication of each vertex of path
be a graph obtained by duplication of each vertex of path 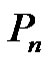 or cycle
or cycle 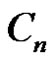 by an edge then
by an edge then 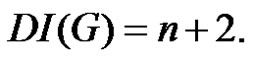
Proof: Let 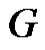 be a graph obtained by duplication of each vertex
be a graph obtained by duplication of each vertex 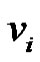 of path
of path 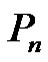 or cycle
or cycle 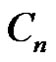 by an edge
by an edge 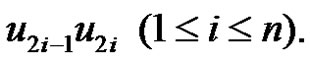 Then from Theorem 2.4 we have
Then from Theorem 2.4 we have 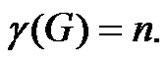 Let
Let 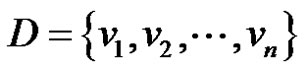 be a γ-set of graph G. Then
be a γ-set of graph G. Then 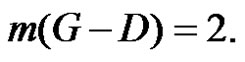 Therefore,
Therefore,
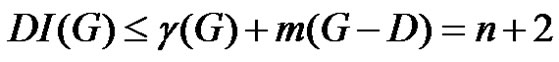 (1)
(1)
We will show that the number 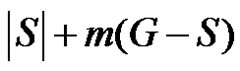 is minimum. For that we have to take into account the minimality of both
is minimum. For that we have to take into account the minimality of both 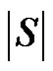 and
and 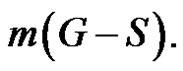 The minimality of
The minimality of 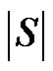 is guaranteed as S is γ-set. Now it remains to show that if S is any dominating set other than D then
is guaranteed as S is γ-set. Now it remains to show that if S is any dominating set other than D then 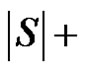
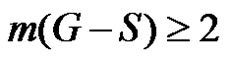 . If
. If 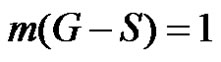 then
then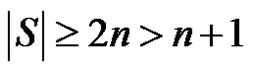 , consequently
, consequently 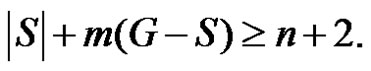 If
If 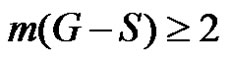 then trivially
then trivially 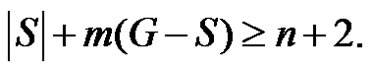 Hence for any dominating set S,
Hence for any dominating set S,
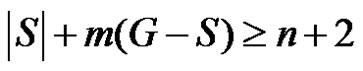 (2)
(2)
From (1) and (2) we have 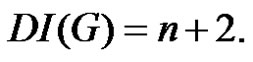
Proposition 2.6 [6]. A dominating set 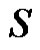 is a minimal dominating set if and only if for each vertex
is a minimal dominating set if and only if for each vertex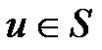 , one of the following two conditions holds:
, one of the following two conditions holds:
1) u is an isolate of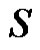 .
.
2) There exists a vertex 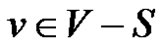 for which
for which 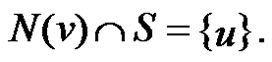
Lemma 2.7. Let G be a graph obtained by duplication of each vertex of wheel 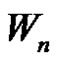 by an edge then
by an edge then 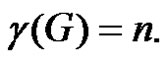
Proof: Let 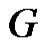 be a graph obtained by duplication of rim vertices as well as apex vertex altogether of wheel
be a graph obtained by duplication of rim vertices as well as apex vertex altogether of wheel 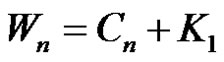 by edges
by edges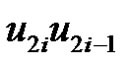 and
and 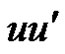 respectively. Then each rim vertex
respectively. Then each rim vertex 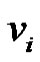 will dominate the vertices
will dominate the vertices 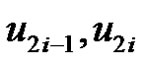 and apex vertex
and apex vertex 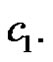 For
For 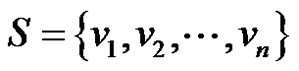 there exists a vertex
there exists a vertex 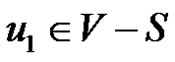 such that
such that 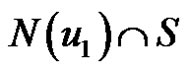 is a singleton set. Then from Proposition 2.6
is a singleton set. Then from Proposition 2.6 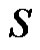 will be a minimal dominating set of
will be a minimal dominating set of 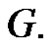 If
If 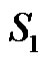 is any dominating set then we claim that
is any dominating set then we claim that 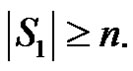 Because
Because
1) If all the elements of 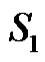 are only of the type
are only of the type 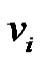 then
then 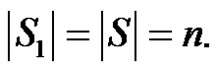
2) If elements of 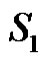 are combination of
are combination of 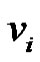 and
and 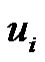 then
then 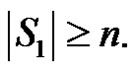
3) If 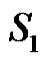 contains any of first two types together with the apex vertex then
contains any of first two types together with the apex vertex then 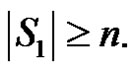
4) If 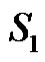 contains
contains 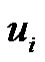 and apex vertex then
and apex vertex then 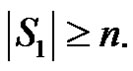
Thus we have 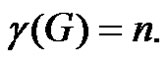
Theorem 2.8. Let 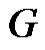 be a graph obtained by duplication of each vertex of wheel
be a graph obtained by duplication of each vertex of wheel 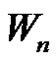 by an edge then
by an edge then 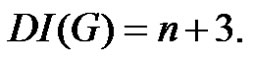
Proof: Let 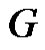 be a graph obtained by duplication of apex vertex
be a graph obtained by duplication of apex vertex 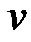 of wheel
of wheel 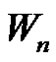 by an edge
by an edge 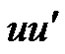 and the rim vertices
and the rim vertices 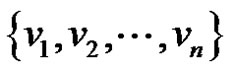 of wheel
of wheel 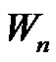 by an edge
by an edge 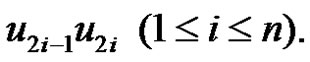 Then from Lemma 2.7 we have
Then from Lemma 2.7 we have 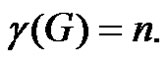 Let
Let 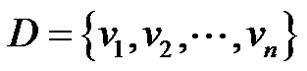 be a γ-set of graph G. Then
be a γ-set of graph G. Then 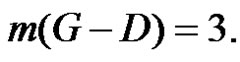 Therefore
Therefore
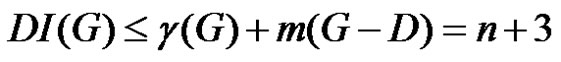 (1)
(1)
We will show that the number 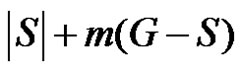 is minimum. For that we have to take into account the minimality of both
is minimum. For that we have to take into account the minimality of both 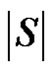 and
and 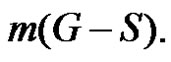 The minimality of
The minimality of 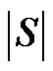 is guaranteed as S is γ-set. Now it remains to show that if S is any dominating set other than D then
is guaranteed as S is γ-set. Now it remains to show that if S is any dominating set other than D then
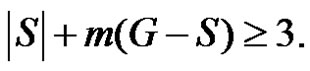
If 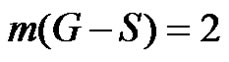 then
then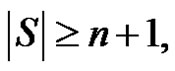 consequently
consequently
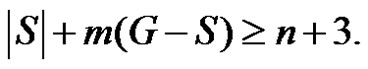
If 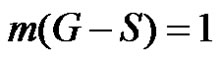 then
then 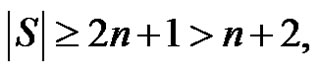 consequently
consequently
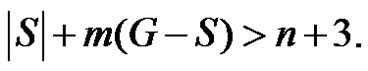
If 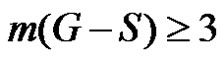 then trivially
then trivially 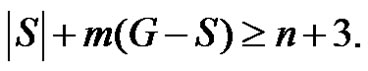 Thus for any dominating set S,
Thus for any dominating set S,
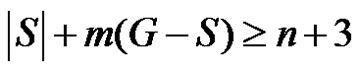 (2)
(2)
Hence from (1) and (2) 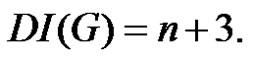
3. Concluding Remarks
We have investigated domination integrity of three special graph families. This work relates to network expansion and measure of vulnerability. We conclude that expansion of network will provide the reason for increase of vulnerability. To investigate similar results for different graph families obtained by various graph operations is an open area of research.
4. Acknowledgements
The authors are highly thankful to the anonymous referee for valuable comments and constructive suggestions.