1. Introduction
Recently a new active building block named as the MMCC [1] is introduced; the element is quite attractive for analog signal conditioning and wave processing applications. Here we present the realization of some simple integrator and differentiator based on the MMCC wherein the time constant  may be tuned electronically by a d.c. control voltage
may be tuned electronically by a d.c. control voltage . The integrators/ differentiators find numerous applications in signal processing and filter design [2,3].
. The integrators/ differentiators find numerous applications in signal processing and filter design [2,3].
The MMCC block here is implemented employing the readily available IC-chips, viz., the ICL-8013 multiplier [4] and a AD-844 CFA [5-7]. Electronic τ-tuning is done by varying  of the multiplier and by changing the polarity of
of the multiplier and by changing the polarity of , an inverting or non-inverting response may be obtained.
, an inverting or non-inverting response may be obtained.
The ICL-8013 device is a four-quadrant analog multiplier whose output is proportional to the electronic product of two input voltage signals with a transmission constant k·volt–1 [4]. The high accuracy (±1%), relatively wide bandwidth (B = 1 MHz) ad improved versatility make it quite suitable for analog signal conditioning and wave processing applications.
The quality factor (Q) of the circuits is shown to be practically active-insensitive relative to the device port errors  of the multiplier and CFA elements. At relatively higher frequencies, the shunt-RC trans-impedance components across the z-node of the CFA device cause some phase deviations which alter the Q-values slightly; these effects had also been examined. The proposed designs have been tested in time-domain for wave conversion applications up to a signal frequency of 600 KHz and satisfactory response are verified by both hardware test and PSPICE simulation. The Q-value indicates a measure of the idealness of the phase properties of integrator/differentiator in frequency domain. The device non-idealities produce very insignificant effects on these phase properties; hence active-insensitive.
of the multiplier and CFA elements. At relatively higher frequencies, the shunt-RC trans-impedance components across the z-node of the CFA device cause some phase deviations which alter the Q-values slightly; these effects had also been examined. The proposed designs have been tested in time-domain for wave conversion applications up to a signal frequency of 600 KHz and satisfactory response are verified by both hardware test and PSPICE simulation. The Q-value indicates a measure of the idealness of the phase properties of integrator/differentiator in frequency domain. The device non-idealities produce very insignificant effects on these phase properties; hence active-insensitive.
2. Analysis
The MMCC block and its proposed device implementation are shown in Figures 1(a) and (b); the nodal equations [1] are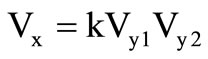 ,
,  and
and . In the proposed configuration, the control voltage
. In the proposed configuration, the control voltage  is used at terminal
is used at terminal  with
with  as the multiplication constant in volt–1 wherein the nominal input stimulus
as the multiplication constant in volt–1 wherein the nominal input stimulus 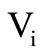 is applied to terminal
is applied to terminal . We could devise either polarity MMCC by changing the sign of
. We could devise either polarity MMCC by changing the sign of  so as to obtain both inverting/non-inverting functions. The CFA nodal relations are
so as to obtain both inverting/non-inverting functions. The CFA nodal relations are ,
,  ,
,  and
and  ; We thus have design convenience with this implementation that provides an additional voltage source output
; We thus have design convenience with this implementation that provides an additional voltage source output , which is not usually available with the conventional current conveyor [8] along with the current source output
, which is not usually available with the conventional current conveyor [8] along with the current source output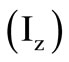 . The CFA port tracking ratios are postulated in the literature [3,9] in terms of finite but small errors
. The CFA port tracking ratios are postulated in the literature [3,9] in terms of finite but small errors  as
as ,
, 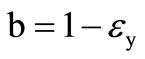 and
and  ; the error vanish
; the error vanish 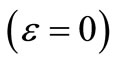 for an ideal element,
for an ideal element,
 (a)
(a) (b)
(b)
Figure 1. The MMCC building block (a) MMCC with nodal relations; (b) MMCC implementation with commercially available chips.
hence we get in Figure 1(b).
 (1)
(1)
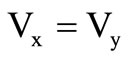 ;
; (2)
(2)
and
 (3)
(3)
with 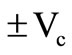 one gets a
one gets a .
.
The proposed integrator/differentiator are obtained after realizing a ratio type  function as shown in Figures 2(a) and (b) after incorporating the RC-components in the building block appropriately so that we could implement design within the single MMCC configuration; analysis by Equations (1) to (3) yields in Figure 2.
function as shown in Figures 2(a) and (b) after incorporating the RC-components in the building block appropriately so that we could implement design within the single MMCC configuration; analysis by Equations (1) to (3) yields in Figure 2.
 (4)
(4)
where  is used as input signal and
is used as input signal and  is control voltage and
is control voltage and  are passive one-port RC impedances. For Figure 2(a) the transfer is non-inverting with positive sign and for Figure 2(b) it is inverting. We select
are passive one-port RC impedances. For Figure 2(a) the transfer is non-inverting with positive sign and for Figure 2(b) it is inverting. We select  and
and , for an ideal integrator so that
, for an ideal integrator so that
 ;
; (5)
(5)
Interchanging the components we get the ideal differentiator
 ;
; (6)
(6)
Thus for a given RC product,  are electronically tunable by
are electronically tunable by .
.
3. Effect of Non-Ideality
The design imperfections of the proposed circuits may be examined in terms of two types device non-idealities, viz., first with respect to parasitic time constant components appearing in shunt at the current source output node-z  of the AD-844 current amplifier. Effect of these transimpedance components becomes dominant at relatively higher frequency operation of the integrator/ differentiator while the parasitic capacitance
of the AD-844 current amplifier. Effect of these transimpedance components becomes dominant at relatively higher frequency operation of the integrator/ differentiator while the parasitic capacitance  affects the quality factor (Q) due to its excess phase. Analyses show that some upper and lower bounds in the operating frequency ranges of the integrator/differentiator are introduced by the parasitic components, albeit this effect could be minimized with suitable design. The second non-ideality is with respect to the finite device port mismatch errors
affects the quality factor (Q) due to its excess phase. Analyses show that some upper and lower bounds in the operating frequency ranges of the integrator/differentiator are introduced by the parasitic components, albeit this effect could be minimized with suitable design. The second non-ideality is with respect to the finite device port mismatch errors  which slightly alters the values of the nominal time constant
which slightly alters the values of the nominal time constant . As per datasheet [5] rz ≈ 5 MΩ and 3 pF ≤ Cz ≤ 6 pF. In the proposed designs we selected
. As per datasheet [5] rz ≈ 5 MΩ and 3 pF ≤ Cz ≤ 6 pF. In the proposed designs we selected  and usually
and usually . Also we expressed
. Also we expressed  volt–1 so that we can essentially write
volt–1 so that we can essentially write  for sensitivity calculation. First we derive the nonideal effects owing to the shunt transimpedance components. The transfer functions for Figure 2(a) then modify to
for sensitivity calculation. First we derive the nonideal effects owing to the shunt transimpedance components. The transfer functions for Figure 2(a) then modify to
 (7)
(7)
and
 (8)
(8)
where
 (9)
(9)
 ;
; ;
; ;
;  (10)
(10)
Table 1 shows the details of the proposed realizations and the corresponding effects of non-ideality due to the device transimpedance components for both Figures 2(a) and (b); here  is the lower bound corner frequency of integrator and
is the lower bound corner frequency of integrator and 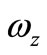 is the upper bound cut-off frequency of differentiator. Above
is the upper bound cut-off frequency of differentiator. Above  corner frequency the integrator becomes practically ideal, and below
corner frequency the integrator becomes practically ideal, and below  cut-off frequency the differentiator becomes practically ideal. For example if rz ≈ 5 Ω, C ≈ 15 pF, Cz ≈ 5.5 pF and R ≈ 3 KΩ, one gets fc ≈ 2 kHz and fz ≈ 10 MHz.
cut-off frequency the differentiator becomes practically ideal. For example if rz ≈ 5 Ω, C ≈ 15 pF, Cz ≈ 5.5 pF and R ≈ 3 KΩ, one gets fc ≈ 2 kHz and fz ≈ 10 MHz.
The port mismatch errors modify the nominal values given by
 ,
, (11)
(11)
which yields the active sensitivity figures as
 ,
, 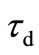 ,
, ;
; 
 (a)
(a) (b)
(b)
Figure 2. Integrator/differentiator design (a) Non-inverting ratio function realization V0/V1 = kVcZ2/Z1; (b) Inverting ration function realization.

Table 1. Effects of transimpedance non-ideality for Figures 2(a) and (b).

Table 2. Summary on performance of some recent oscillators.
where 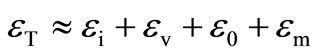 and
and . It may be shown similarly that the active-Q sensitivities are also extremely low.
. It may be shown similarly that the active-Q sensitivities are also extremely low.
4. Quadrature Linear VCO Design
We next present the design of a MMCC based Dual Integrator Loop (DIL) sinusoid oscillator (involving one noninverting and the other inverting type). The feature of four quadrant operation of the multiplier device is utilized here for realizing the opposite polarity ideal integrators by using a bipolar d.c. control voltage (±Vc). A linear fo-tuning law in a range of 40 KHz ≤ fo ≤ 600 KHz with satisfactory quadrature signal generation had been measured both by PSPICE macromodel simulation [9] and with hardware circuit implementation. The oscillation frequency is  where
where 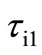 and
and  denote time constants of the two MMCC-based integrators in loop. The frequency stability factor
denote time constants of the two MMCC-based integrators in loop. The frequency stability factor  of a sinusoid oscillator is defined as
of a sinusoid oscillator is defined as 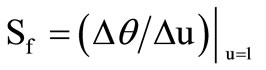 where
where  and
and  is the loop phase shift. We evaluated the value of
is the loop phase shift. We evaluated the value of  after assuming finite trans-admittance parameters, given by
after assuming finite trans-admittance parameters, given by 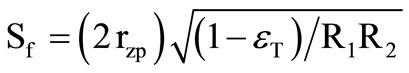 where
where 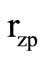 is the shunt equivalent
is the shunt equivalent  of the
of the  components for the two integrator stages. The stability is quite satisfactory
components for the two integrator stages. The stability is quite satisfactory  since
since . Here both capacitors are grounded [10] and the parasitic capacitances
. Here both capacitors are grounded [10] and the parasitic capacitances  have an additive effect
have an additive effect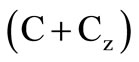 ; but since value of C is chosen such that
; but since value of C is chosen such that 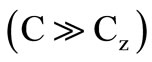 the resulting deviation would be insignificant, or alternatively, the effect of
the resulting deviation would be insignificant, or alternatively, the effect of  may be pre-absorbed in value of C.
may be pre-absorbed in value of C.
Analysis on the effects of device port mismatch errors 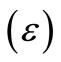 indicate that
indicate that 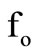 is practically active insensitive and the effects of the shunt parasitic components of the CFAdevice are negligible. The frequency stability
is practically active insensitive and the effects of the shunt parasitic components of the CFAdevice are negligible. The frequency stability  factor of the proposed oscillator is quite high
factor of the proposed oscillator is quite high  at low values of measured THD (≈1.1%). Integrators/differentiators are useful as filters, phase compensators and delay measuring blocks; double integrator loops are useful as quadrature signal generators which had been proposed here with linear electronic tuning properties.
at low values of measured THD (≈1.1%). Integrators/differentiators are useful as filters, phase compensators and delay measuring blocks; double integrator loops are useful as quadrature signal generators which had been proposed here with linear electronic tuning properties.
5. Experimental Results
The proposed circuits were tested for wave conversion application by both hardware test and PSPICE simulation. Some simulation results for square wave to triangular wave conversion by integrator and vice versa for the differentiator are shown in Figure 3 with inverting/noninverting polarity. The multiplier constant is set to k = 0.5/volt and the passive components are suitably chosen for the measurement in a frequency range of 50 KHz ≤ f ≤ 600 KHz. Both PSPICE simulation and hardware circuit tests were carried out using AD-844 CFAS Op-amp and ICL 8013 multiplier device; additionally AD-534 multiplier element had also been used to verify the results.
With hardware circuit test, however, a deviation of 2% - 5% in the response had been observed; this may be due to the inter-lead stray capacitance between the chip terminal and the breadboard pin. With sinusoid excitation, the desired phase shift of ±π/2 had been verified and a phase error of less than 1˚ had been measured at 900 KHz; expected 6 db/octave attenuation for the integrator and accentuation for the difference in magnitude response had also been measured. It may be mentioned that that the operating range of the circuits concomitant to the bandwidth (=1 MHz) of the ICL-8013 device; embedding the HA 2557 multiplier device [4] with bandwidth equal to 130 MHz is expected to yield an extended frequency range. The error analysis has been carried out here following the model of non-idealities and their subsequent effects on the nominal design as per the relevant recent literature survey cited in Table 2 [11-15].
6. Conclusion
Some new inverting/non-inverting voltage tunable inte-
grator and differentiator realizations are presented using the recent MMCC device. The chip level design implementation is done by the readily available elements, viz., the ICL-8013 or AD-534 four-quadrant multiplier and the AD-844 CFA unity-gain current amplifier. The quality factor (Q) of the circuits is practically active—insensitive. Satisfactory response had been measured in a range of 50 kHz ≤ f ≤ 600 kHz with suitable design. Measured phase error is less than 1˚ at 900 kHz. Application to wave conversion had been verified for both the integrator and differentiator function while electronic tuning of τi,d with respect to control voltage is obtained satisfactorily. Subsequently a double-integrator loop sine wave quadrature oscillator had been designed and its electronic tuning property is tested in a range of 40 KHz ≤ fo ≤ 600 KHz. Experimental results are shown in Figure 4. The MMCC is a recently proposed active building block; its application to the design of such integrator/differentiator and linear quadrature VCO had not yet been reported. The VCO is a useful element for PLL or FM discriminator design. The authors are now carrying out further work to extend the functionality of the VCO so as to implement a digitally programmable oscillator wherein a digital code (e.g. BCD word), after being con-
 (a)
(a)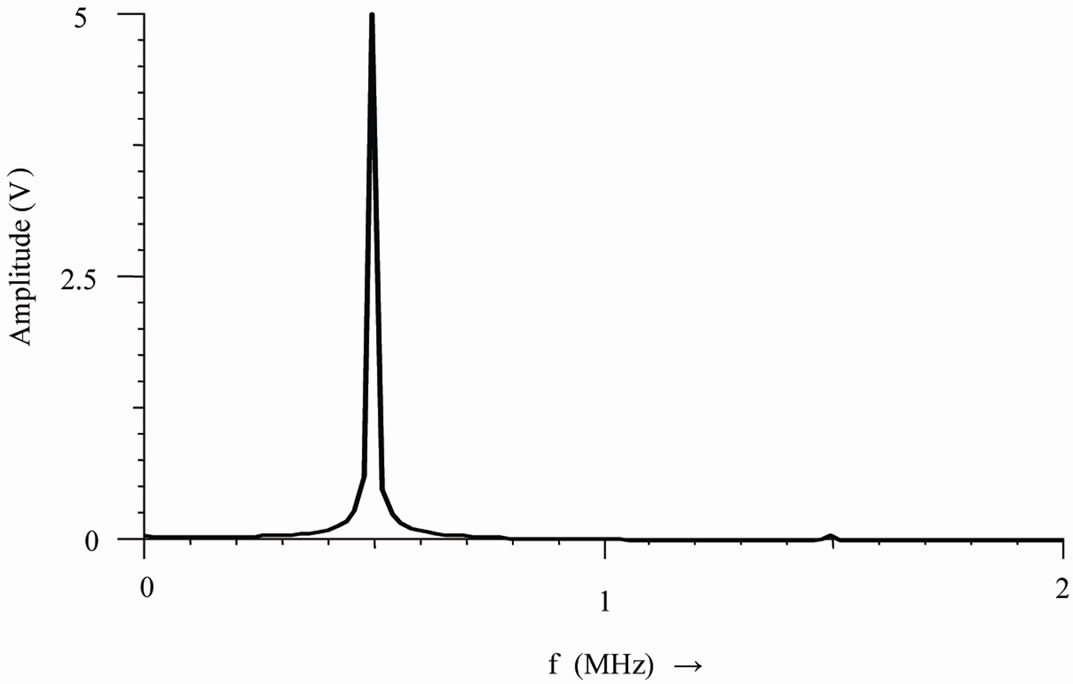 (b)
(b) (c)
(c)
Figure 4. Response of dual-integrator loop quadrature oscillator: (a) Simulated response at fo = 500 KHz with k = 0.1/volt and Vc = 5 V.d.c.; (b) Spectrum of the generated signal; (c) Linear tuning characteristics with C = 160 pF:R = 1 KΩ (●); R = 2 KΩ (○) (dotted line by hardware test).
verted by a D to A Converter (DAC), would be able to tune and generate a sequence of frequencies leading to FSK/PSK type modulation signal.