Well Behaved Parametric Class of Exact Solutions of Einstein-Maxwell Field Equations in General Relativity ()
1. Introduction
Ever since the formulation of Einstein-Maxwell field equations, the relativists have been proposing different models of immense gravity astrophysical objects by considering the distinct nature of matter or radiation (energy-momentum tensor) present in them. Such models successfully explain the characteristics of massive objects like quasar, neutron star, pulsar, quark star, blackhole or other super-dense object. These stars are specified in terms of their masses as white dwarfs (Mass < 1.44 solar mass), Quark star (2 solar mass - 3 solar mass) and Neutron star (1.35 solar mass - 2.1 solar mass).
It is well known that the Reissener-Nordstrom solution for the external field of a ball of charged mass has two distinct singularities at finite radial positions other than at the centre. Thus the solution describes a bridge (worm hole) between two asymptotically flat spaces and an electric flux flowing across the bridge. Graves and Bill [1] pointed out that the region of minimum radius or the throat of worm hole pulsates periodically between these two surfaces due to Maxwell pressure of the electric field. Consequently, unlike Schwarzschild’s exterior solution of chargeless matter,in Reissener-Nordstrom solution has no surface which can catastrophically hit the geometric singularity at r = 0. All these aspects show that the presence of some charge in a spherical material distribution provides an additional resistance against the gravitational contraction by mean of electric repulsion and hence,the catastrophic collapse of the entire mass to a point singularity can be avoided.
The above result has been supported by a physically reasonable charge spherical model of Bonnor [2], that a dust distribution of arbitrarily large mass and small radius can remain in equilibrium against the pull of gravity by a repulsive force produced by a small amount of charge. Thus it is desirable to study the implications of Einstein-Maxwell field equations with reference to the general relativistic prediction of gravitational collapse. For this purpose charged fluid ball models are required. The external field of such ball is to be matched with Reissener-Nordstrom solution.
For obtaining significant charged fluid ball models of Einstein-Maxwell field equations, the Astrophysicists have been using exact solutions with finite central parameters of Einstein field equations, as seed solutions. There are two type of exact solutions of this category.
Type 1. If the solutions are well behaved (DelgatyLake [3], Pant [4]). These solutions their self completely describe interior of the Neutron star or analogous super dense astrophysical objects with chargeless matter. Delgaty-Lake [3] studied most of the exact solutions so far obtained and pointed out that only nine solutions are regular and well behaved. Out of which only six of them are well behaved in curvature coordinates and rest three solutions are in isotropic coordinates. In previous papers (Pant et al. [5], Pant [4], we obtained a new well behaved solution in isotropic coordinates and two new well behaved solutions in curvature coordinates respectively.
Type 2. If the solutions are not well behaved but with finite central parameters, such solutions are taken as seed solutions of astrophysical objects with charge matter since at centre the charge distribution is zero.
For well behaved nature of the solution in curvature coordinates, the following conditions should be satisfied (augmentation of (Delgaty-Lake [3] and Pant [4]) conditions).
1) The solution should be free from physical and geometrical singularities i.e. finite and positive values of central pressure, central density and non zero positive values of  and
and  i.e.
i.e. 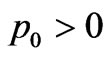 an
an . For well behaved solution in curvature coordinates, it should have
. For well behaved solution in curvature coordinates, it should have , i.e. the tangent-3 space at the centre in flat but converse is not true.
, i.e. the tangent-3 space at the centre in flat but converse is not true.
2) The solution should have positive and monotonically decreasing expressions for pressure and density ( ) with the increase of r. The solution should have positive value of ratio of pressure-density and less than 1 (weak energy condition) and less than 1/3 (strong energy condition) throughout within the star.
) with the increase of r. The solution should have positive value of ratio of pressure-density and less than 1 (weak energy condition) and less than 1/3 (strong energy condition) throughout within the star.
3) The solution should have positive and monotonically decreasing expression for fluid parameter 
with the increase of r, i.e.
 and
and 
and  is negative valued function for
is negative valued function for .
.

where  is adiabatic index and for realistic matter
is adiabatic index and for realistic matter . Thus we have,
. Thus we have,  decreases with the increase of r.
decreases with the increase of r.
4) The solution should have positive and monotonically decreasing expression for velocity of sound 
with the increase of r and causality condition should be obeyed at the centre i.e. .
.
5) The red shift Z should be positive, finite and monotonically decreasing in nature with the increase of r.
6) Electric intensity E is positive and monotonically increasing from centre to boundary and at the centre the Electric intensity is zero.
Under these well behaved conditions, one has to assume the gravitational potential and electric field intensity in such a way that the field equation can be integrated and solution should be well behaved. Keeping in view of this aspect, several authors obtained the parametric class of exact solutions Pant et al. [6,7], Gupta and Maury [8,9], Pant [10], M. J. Pant and Tewari [11] etc. These coupled solutions are well behaved with some positive values of charge parameter K and completely describe interior of the super-dense astrophysical object with charge matter. Further, the mass of the such modeled super dense object can be maximized by assuming surface density is ρb = 2 × 1014 g/cm3. In the present paper we have obtained yet another new parametric class of well behaved exact solutions of Einstein-Maxwell field equations, which is compatible within the range of Quark star and neutron star.
2. Einstein-Maxwell Equation for Charged Fluid Distribution
Let us consider a spherical symmetric metric in curvature coordinates
 (1)
(1)
where the functions  and
and  satisfy the Einstein-Maxwell equations
satisfy the Einstein-Maxwell equations
 (2)
(2)
where 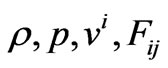 denote energy density, fluid pressure, velocity vector and skew-symmetric electromagnetic field tensor respectively.
denote energy density, fluid pressure, velocity vector and skew-symmetric electromagnetic field tensor respectively.
In view of the metric (1), the field Equation (2) gives
 (3)
(3)
 (4)
(4)
 (5)
(5)
where, prime (/) denotes the differentiation with respect to r and q(r) represents the total charge contained within the sphere of radius r.
Now let us set
 (6)
(6)
which is the same as that of the metric obtained by Adler [12].
Putting (6) into (3)-(5), we have
 (7)
(7)
 (8)
(8)
and Z satisfying the equation
 (9)
(9)
where .
.
Our task is to explore the solutions of equation (9) and obtain the fluid parameters  and
and  from equation (7) and equation (8).
from equation (7) and equation (8).
3. New Class of Solutions
In order to solve the differential equation (9), in this paper we consider the electric intensity E of the following form
 (10)
(10)
where K is a positive constant. The electric intensity is so assumed that the model is physically significant and well behaved i.e. E remains regular and positive throughout the sphere. In addition, E vanishes at the centre of the star.
In view of equation (10) differential equation (9) yields the following solution
 (11a)
(11a)
where A is an arbitrary constant of integration.
 (11b)
(11b)
Using (11a), (11b) into equations (7) and (8), we get the following expressions for pressure and energy density
 (12)
(12)
 (13)
(13)
4. Properties of the New Class of Solutions
The central values of pressure and density are given by
 (14)
(14)
 (15)
(15)
For 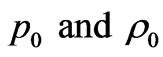 must be positive and
must be positive and , we have
, we have
 , and
, and  (16)
(16)
Differentiating (12) and (13) w. r. t. x, we get;
 (17)
(17)
 (18)
(18)
 (19)
(19)
The expression of right hand side of (19) is negative, thus the pressure p is maximum at the centre and monotonically decreasing.
 (20)
(20)

 (21)
(21)
The expression of right hand side of (20) is negative, the density  is maximum at the centre and monotonically decreasing.
is maximum at the centre and monotonically decreasing.
And hence the velocity of sound v is given by the following expression

 (22)
(22)
 , for all values of K and A satisfied by (16).
, for all values of K and A satisfied by (16).
The expression for gravitational red-shift (z) is given by
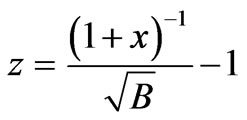 (23)
(23)
The central value of gravitational red shift to be non zero positive finite, we have
 (24)
(24)
Differentiating Equation (24) w.r.t. x, we get,
 (25)
(25)
The expression of right hand side of (25) is negative, thus the gravitational red-shift is maximum at the centre and monotonically decreasing.
Differentiating equation (10) w.r.t. x, we get,
 (26)
(26)
 (27)
(27)
The expression of right hand side of (27) is positive, thus the electric intensity is minimum at the centre and monotonically increasing for all values of K > 0. Also at the centre it is zero.
5. Boundary Conditions
The solutions so obtained are to be matched over the boundary with Reissner-Nordstrom metric.
 (28)
(28)
which requires the continuity of  across the boundary
across the boundary .
.
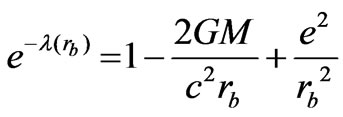 (29)
(29)
 (30)
(30)
 (31)
(31)
 (32)
(32)
The condition (30) can be utilized to compute the values of arbitrary constants A as follows:
On setting  (
( being the radius of the charged sphere)
being the radius of the charged sphere)
Pressure at  gives
gives
 (33)
(33)
The expression for mass can be written as
 (34)
(34)
In view of (29) and (30) we get,
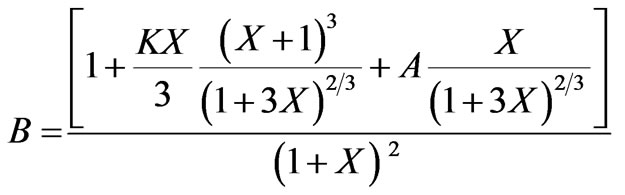
Centre red shift is given by
 (35)
(35)
In view of and TableI and Table-II We observe that pressure, density, pressure-density ratio, square of adiabatic sound speed and gravitational red shift decrease monotonically with the increase of radial coordinate however, the charge distribution is increasing in nature.
6. Discussion
In view of and Tables 1 and 2, it has been observed that all the physical parameters (p,  ,
, 
and E) are positive at the centre and within the limit of realistic equation of state and well behaved conditions for all values of K satisfying the inequalities 0.72 ≤ K ≤ 2.41. However, corresponding to any value of K < 0.72, there exist no value of X for which the nature of adiabatic sound speed is monotonically decreasing from centre to pressure free interface and for K > 2.41, the pressure is negative some where within the ball for all values of X. It has been observed that under well behaved conditions this class of solutions gives us the mass of super dense object within the range of quark star and neutron star.
We now present here two models of super dense star based on the particular solution discussed above by assuming surface density; ρb = 2 × 1014 g/cm3. Corresponding to K = 0.72 with X = 0.15, the resulting well behaved model has the mass M = 1.94 MΘ.with radius rb » 15.2 km and for K = 2.41 with X = 0.15, the resulting well behaved model has the mass M = 2.26 MΘwith radius rb » 14.65 km.
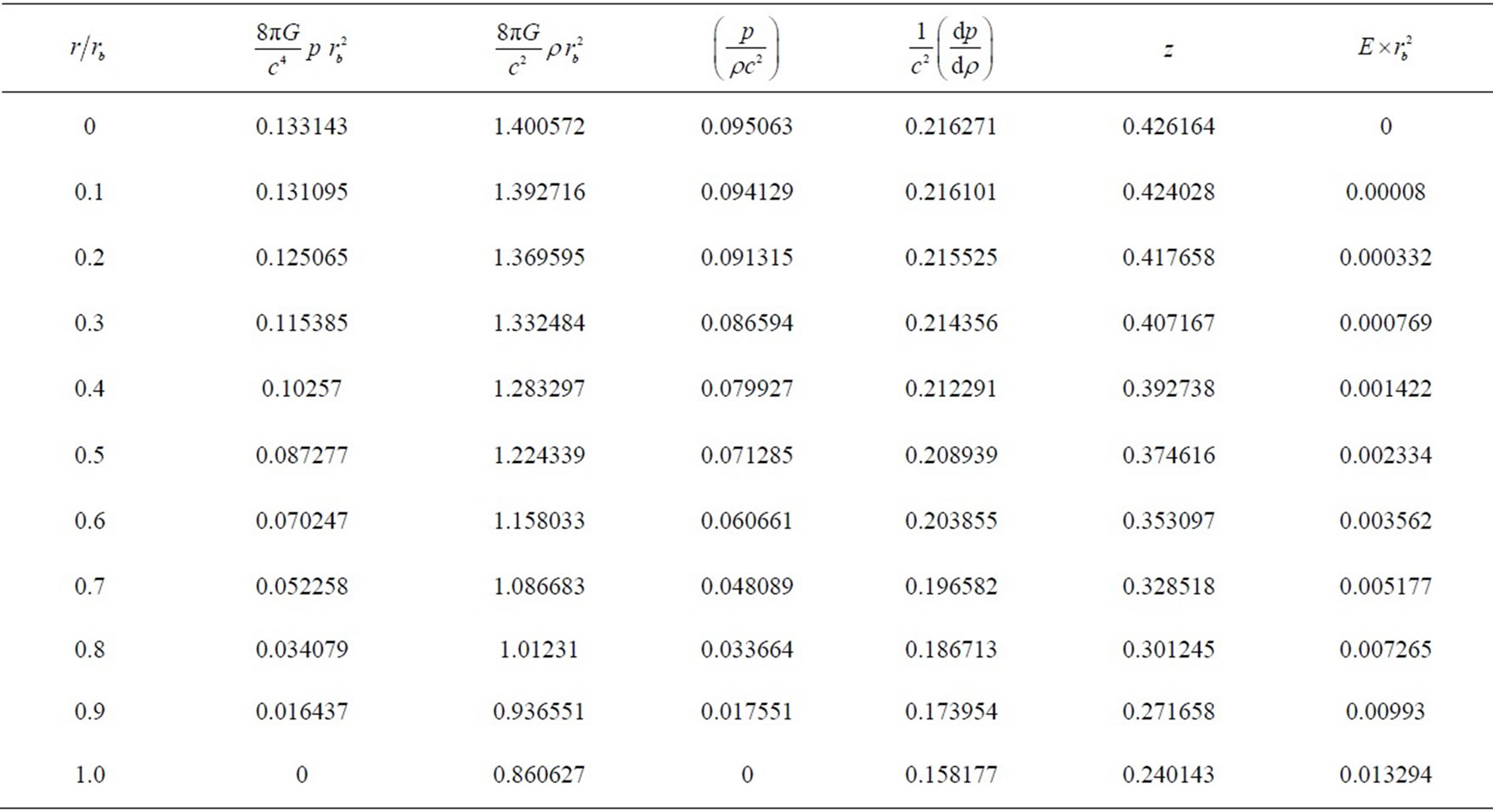
Table 1. The march of pressure, density, pressure-density ratio, square of adiabatic sound speed, gravitational red shift and electric field intensity within the ball corresponding to K = 0.72 with X = 0.15.

Table 2. The march of pressure, density, pressure-density ratio, square of adiabatic sound speed, gravitational red shift and electric field intensity within the ball corresponding to K = 2.41 with X = 0.15.
7. Acknowledgements
1) First author (NP) acknowledges his gratitude to Lt. Gen. Jatinder Singh AVSM, SM, Comdt, NDA for his motivation and encouragement.
2) First author (NP) also acknowledges his gratitude to Prof A. N. Srivastava HOD Mathematics NDA for his invaluable suggestions.