
1. Introduction
The inverse eigenvalue problem for pseudo-symmetric matrices (PIEP) is the issue of reconstructing a matrix with a prespecified structure from given eigendata. For example, Xu [1] reconstructed the pseudo-Jacobi matrix using its spectrum and the spectra of the two complementary principal matrices. Following this, Xu [2] [3] reconstructed both the modified pseudo-Jacobi matrix and the doubly periodic pseudo-Jacobi matrix. Su [4] [5] reconstructed the pseudo-Jacobi matrix and a special acyclic matrix using the spectral data obtained from its matrix. In addition to the previously discussed inverse spectral problem for pseudo-symmetric matrices, we know that one means of describing the structuring of a matrix is to denote it by its corresponding graph, and several authors have investigated the problem of describing the inverse of a constructed matrix in terms of a graph. As in references [6] [7] [8] [9] has investigated inverse eigenvalue problems for certain matrices with special graphics. Moreover, the literature [10] [11] [12] [13] has examined inverse eigenvalue problems for matrices utilized in different fields, including mechanical vibration, control theory, pole distribution and graph theory.
Given an
symmetric matrices
, the graph of A, denoted as
, is a graph that comprises vertex set
and edge set
. For a graph G with n vertices,
denotes the set of all
symmetric matrices which have G as their graph. An acyclic matrix is a matrix whose graph forms a double starlike tree [13] . Simple examples of acyclic matrices include those with graph representations as paths, stars, and banana trees.
The focal point of this paper is to investigate the inverse eigenvalue problem for pseudo-symmetric matrices with the graph as an
-banana tree when all
and referred to as PIEPB
. An
-banana tree, is a graph created by attaching one leaf of each of c copies of a s-star graph with a single root vertex that is distinct from all the stars, where
and
, marked as follows: the root vertex is labeled by 1, the vertices of distance 1 from the root vertex as the intermediate vertices is labeled by
, the center of every (
) is labeled by
and leaves of the center is labeled by
(Figure 1), defined in [14] , research on banana trees in literature [15] [16] . For example matrix
of an
-banana tree is of the following form:
,
Based on the inverse spectral problem for matrices whose graph is a banana tree, we improve their matrices and continue to study the inverse spectral problem for the pseudo-symmetric matrices. For example pseudo-symmetric matrix
is of the following form
,
where main diagonal
and the two first lower and upper off-diagonals
and
, with all
and all
. If all
, the pseudo-symmetric matrix
changed to the symmetric matrix
.
PIEPB
. Given different numbers
,
construct an
matrix
such that
and
are the eigenvalues of
, the leading principal submatrix of A, respectively.
The structure of this work is organized as follows. In Sect.2, some properties of pseudo-symmetric matrix
were given. In Sect.3, the necessary and sufficient conditions for the solvability of an inverse eigenvalue problems of pseudo-symmetric matrix
. In Sect.4, the evolutionary plots of the distribution of eigenvalues of low-order leading principal submatrix were drawn through algorithm and numerical simulation, indicating the accuracy of the result. Finally, in Sect.5, the conclusions are presented.
2. Preliminaries
Lemma 2.1. Let
and let
be the
leading principal submatrix of A, with characteristic polynomial
. Then the sequence
satisfies the recurrence formulae
,
,
,
,
.
where
is the submatrix row and columns
of the matrix
,
and
when
.
Lemma 2.2. Let
, then
and
have no common root.
Proof. Supposing that
is a common root of
and
, by Lemma 2.1, we get that
is also a root of
, and so we have
, Which is a contradiction. Hence
and
have no common root.
Lemma 2.3. ( [8] ) Let
be a monic polynomial of degree n, with all real zeroes. If
and
are, respectively, the smallest and largest zero of
, then
(1) If
, we have that
,
(2) If
, we have that
.
Lemma 2.4. ( [15] ) Let all
for
,
and
, respectively, be the smallest and largest eigenvalues of its
leading principal submatrix
,
. Then we have
,
and
.
Lemma 2.5. The sufficient and necessary conditions for the existence of symmetric matrix
whose graph is an
-banana tree, such that
and
are the smallest and largest eigenvalue of
, the leading principal submatrix of A, respectively, is
. (1)
Proof. Sufficiency: suppose that
satisfies (1) for
. To prove the existence of a symmetric matrix
with the required properties is equivalent to going to prove that the system
(2)
For
, it is immediate that
.
According to Lemma 2.1,
for
, system (2) can be written as
,
by condition (1) and Lemma 2.3, we get
,
,
, and
, then
,
.
According to Lemma 2.1,
for
, system (2) can be written as
by condition (1) and Lemma 2.3, we have
and
then
,
.
According to Lemma 2.1,
for
, system (2) can be written as
,
by condition (1), Lemma 2.3 and Lemma 2.4, we get
,
,
,
,
,
, then
,
.
Necessity: Assuming that there exists a unique matrix
such that
and
are the smallest and maximal eigenvalues of their corresponding principal submatrices, respectively, and by Cauchy's alternating theorem and Lemma 2.4, (1) holds.
3. Results
3.1. The Solution of PIEPB
Theorem 3.1. Let different numbers
, if
, (3)
, (4)
(5)
where
, then there exists a matrix
, such that
and
are, respectively, the eigenvalues of
.
Proof. Sufficiency: suppose the conditions (3) (4) and (5) hold. To prove the existence of a pseudo-symmetric matrix
is equivalent to proving that
(6)
When
, it is immediate that
.
According to Lemma 2.1 for
, system (6) can be written as
,
by Lemma 2.3, we have
, (7)
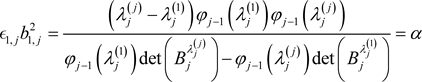 .
.
according to Lemma 2.2,
, added to condition (3), we get
, and
,
. (8)
According to Lemma 2.1 for
, system (6) can be written as
,
by Lemma 2.3, we get
, (9)
.
according to Lemma 2.2,
, added to condition (4), we get
, and
,
. (10)
According to Lemma 2.1 for
, system (6) can be written as
,
by Lemma 2.3, we have
, (11)
.
according to Lemma 2.2,
, added to condition (5), we get
, and
,
. (12)
Conversely. Suppose that PIEPB
has a unique solution, i.e., the system (6) has solutions
and satisfies all
. In the same way that we proved the sufficiency, we get (7)-(12). Thus (3), (4) and (5) hold.
3.2. Algorithm 1
4. Numerical Examples
4.1. Example 1
Table 1, which satisfy conditions (1). By applying MatlabR2021b, we compute the following matrix.
![]()
Table 1. Spectral data for Lemma 2.5.
.
Recompute that: the eigenvalues of its the leading principal submatrices
,
, are:
,
,
,
,
,
,
,
,
.
4.1. Example 2
Given different real number
,
,
,
,
,
,
,
,
,
,
. construct a matrix
, such that
and
are the eigenvalues of
, respectively. In particular, this matrix corresponds to the graph is an (1, 5)-banana tree when all
(Figure 2).
By applying algorithm 1 and matlabR2021b, we compute the following matrix
.
Recompute that: the eigenvalues of its the leading principal submatrices
,
, are:
.
.
.
.
.
.
Figure 3 displays the extreme eigenvalues of
, as presented in example 1. These are in line with the recomputed eigenvalues of
. Likewise, Figure 4 presents the eigenvalues of
, as featured in example 4.2, which are consistent with the recomputed eigenvalues of
.
![]()
Figure 3. Distribution of eigenvalues of
in example 1.
![]()
Figure 4. Distribution of eigenvalues of
in example 2.
5. Conclusion
Based on matrices whose graph is a banana tree, we study the inverse spectral problem for pseudo-symmetric matrices. It is obviously difficult to reconstruct the pseudo-symmetric matrix given the eigenvalues, and in order to achieve this deficiency, other constraints are added on top of the eigendata, which in turn enables the reconstruction of the pseudo-symmetric matrix. We obtained sufficient necessary conditions to solve the problem.
Acknowledgements
This research was supported by the National Nature Science Foundation of China and Shanxi Province Basic Research Program Grant (202203021211088).