A New Physics Would Explain What Looks Like an Irreconcilable Tension between the Values of Hubble Constants and Allows H₀ to Be Calculated Theoretically Several Ways

Claude Mercier

Independent Researcher, Baie-Comeau, Canada.

DOI: 10.4236/jmp.2021.1212098                

Abstract

Observing galaxies receding from each other, Hubble found the universe’s expansion in 1929. His law that gives the receding speed as a function of distance implies a factor called Hubble constant H₀. We want to validate our theoretical value of H₀ ≈ 72.09548580(32) km⋅s^-1⋅MParsec^-1 with a new cosmological model found in 2019. This model predicts what may look like two possible values of H₀. According to this model, the correct equation of the apparent age of the universe gives ~ 14.14 billion years. In approximation, we get the well-known equation 1/H₀ ≈ 13.56 billion years. When we force these ages to fit the 1/H₀ formula, it gives two different Hubble constant values of ~69.2 and 72.1 km⋅s^-1⋅sdot;MParsec^-1. When we apply a theoretical correction factor of η ≈ 1.042516951 on the first value, both target the second one. We found 42 equations of H₀ linking different physics constants. Some are used to measure H₀ as a function of the average temperature T of the Cosmological Microwave Background and the universal gravitational constant G:

H₀ ≈ 72.06(90) km⋅s-¹⋅MParsec^-1 from T by Cobra probe & Equation (16)

H₀ ≈ 71.95(50) km⋅s^-1⋅MParsec^-1 from T by Partridge & Equation (16)

H₀ ≈ 72.086(36) km⋅s^-1⋅MParsec^-1 from G & Equation (34)

H₀ ≈ 72.105(36) km⋅s^-1⋅MParsec^-1 from G & Equations (74), (75), or (76). With 508 published values, H₀ ≈ 72.0957 ± 0.33 km⋅s^-1⋅MParsec^-1 seems to be the “ideal” statistical result. It validates our model and our theoretical H₀ value which are useful to find various interactions with the different constants. Our model also explains the ambiguity between the different universe’s age measurements and seems to unlock a tension between two H₀ values.

Keywords

Hubble Constant H₀, Hubble Tension, Age of the Universe

1. Introduction

In astrophysics, the Hubble constant H₀ [1] is a parameter to analyze the universe. Nevertheless, it is also one of the lesser-known values.

In 1916, Einstein found the general relativity laws [2]. His equations expect that the universe is either expanding or in a Big Crunch. He could have been the first to predict the universe’s expansion, but influenced by the popular idea, Einstein forced his model to be static with a cosmological constant Λ. In 1922, Friedmann showed from relativity that the universe expands at a calculable rate [3]. In 1927, Georges Lemaitre published independent research [4], giving what is now known as Hubble’s law. In 1929, Hubble discovered the universe’s expansion [1]. Equation (1) gives Hubble’s law, with $v$ being the receding speed in km·s⁻¹, D being the distance between the observed object and the observer, and H₀ being the Hubble constant. He measured about H₀ ≈ 500 km·s⁻¹·MParsec⁻¹. His high value was due to a wrong calibration of the cepheids used to evaluate distances. Hubble’s law was correct, but H₀ was remaining to be found with accuracy.

$v=D{H}_0$ (1)

Physicists get H₀ based on far cosmic objects (Cepheids, supernovae, red giants, etc.) or local measurements (CMB, universal gravitational constant G, etc.). Including error margins of published values (see the software in Annex A), H₀ is between 19 to 174 km·s⁻¹·MParsec⁻¹. However, two values are often measured ~69.2 and ~72.1 km·s⁻¹·MParsec⁻¹. An irreconcilable tension between some H₀ values shows up [5]. Even with good accuracies, their error margins do not always overlap. It may let us think that only one of these values is right. No one considered it possible that both values may be in some way correct.

In 2019, we wrote an article [6] explaining what may look like two values for H₀. We calculated the universe age, obtained a result of complex type, and an apparent age of the universe of ~14.4 billion years. The complete equation may be approximated by 1/H₀, giving ~13.56 billion years. We notice that there is a difference of ~4.25% between the approximated and the non-approximated values.

Cosmologists use 1/H₀ to calculate the universe’s age. Thus, if we could measure the apparent age of the universe with no approximation, we would conclude wrongly that the Hubble constant is ~4.25% lower than it should be.

We hypothesize that two values of H₀ are somehow obtained from an approximated and non-approximated equation of the apparent age of the universe. The confusion leads to a tension between two values when there should be only one.

We summarize our cosmological model [6] to get H₀ as a function of α, c, and r_e. We found ways to measure H₀ locally by using the Cosmological Microwave Background (CMB) temperature T and by using the universal gravitational constant G [6] [7]. Based on our model, we found a theoretical equation to calculate H₀ from CODATA values (Committee of Data for Science and Technology) [8].

$\begin{array}{l}{H}_0=\frac{c{\alpha }^{19}\sqrt{\beta }}{r_e}\approx 72.09548580\left(32\right)\text{km}\cdot {\text{s}}^{-1}\cdot {\text{MParsec}}^{-1}\\ \text{where}\beta =3-\sqrt{5}\approx 0.76\end{array}$ (2)

We want to validate this theoretical value of H₀ and highlight the tension between two measured values of H₀. We list the results of the most recent measures of H₀ and build a graph showing someway the popularity of each H₀ value range.

We list 42 H₀ equations. Certain overcome the difficulties to do experimental measurements. We use one of them as a third measurement of H₀. Our cosmological model shows that H₀ and the speed of light are not constant.

2. Physics Parameters

A compact form of notation is used to display tolerances (i.e., 2.734(10) K means 2.734 ± 0.010 K). The CODATA 2014 [8] is used to compare the results of our new equations with the articles published in 2019 and 2020.

Light speed in a vacuum $c=\text{2}99792458\text{m}\cdot {\text{s}}^{-\text{1}}$

Permeability of free space ${\mu }_0=\text{4}\pi \times {10}^{-7}{\text{NA}}^{-\text{2}}$

Permittivity of free space ${\epsilon }_0\approx 8.854187817\times {10}^{-12}\text{F}\cdot {\text{m}}^{-\text{1}}$

Universal gravitational constant $G\approx 6.67408\left(31\right)\times {10}^{-11}{\text{m}}^{\text{3}}\cdot {\text{kg}}^{-\text{1}}\cdot {\text{s}}^{-\text{2}}$

Electron rest mass $m_e\approx 9.10938356\left(11\right)\times {10}^{-31}\text{kg}$

Classical electron radius $r_e\approx 2.8179403227\left(19\right)\times {10}^{-15}\text{m}$

Electron charge $q_e\approx -1.6021766208\left(98\right)\times {10}^{-19}\text{C}$

Planck length $L_p\approx 1.616229\left(38\right)\times {10}^{-\text{35}}\text{m}$

Planck time $t_p\approx 5.39116\left(13\right)\times {10}^{-44}\text{s}$

Planck mass $m_p\approx \text{2}.176470\left(51\right)\times {10}^{-\text{8}}\text{kg}$

Planck constant $h\approx 6.626070040\left(81\right)\times {10}^{-34}\text{J}\cdot \text{s}$

Fine-structure constant $\alpha \approx 7.2973525664\left(17\right)\times {10}^{-3}$

Boltzmann constant $k_b\approx 1.38064852\left(79\right)\times {10}^{-23}\text{J}\cdot {\text{K}}^{-\text{1}}$

Rydberg constant $R_{\infty }\approx 10973731.568508\left(65\right){\text{m}}^{-1}$

3. Summary of our Theory

Our theory is based on a cosmological model officially shown in 2019 [6], but it summarizes papers we wrote at www.pragtec.com/physique since 2011. First, we outline some main milestones as we did in 2020 [7].

3.1. Our Cosmological Model

We hypothesize that there was one expanding sphere containing all matter at the Big Bang. There was no light. After ~360000 years [9], electrons became free to move because of a lower density universe, and the light appeared and began to travel through space, creating a 4-D expanding sphere called the “luminous universe”. As the matter cannot travel as fast as light [10], it created a smaller 4-D expanding sphere, the “material universe”, imbricated in the “luminous universe”.

Einstein found that the presence of a massive object reduces the speed of light v_L [11]. Schwarzschild calculated v_L in a context of a weak gravitational field Φ using general relativity [12]. With |Φ| << c² around a spherical mass, Equation (3) gives v_L as a function of c and a local refractive index n₀ (function of G [13] ).

$v_L\left(r\right)=\frac{c}{n_0}\text{where}{n}_0=\sqrt{\frac{1-2\Phi /c^2}{1+2\Phi /c^2}}\text{and}\Phi =\frac{-Gm}{r}\le 0$ (3)

From an observer on Earth, c seems constant. However, the knowledge of a precise value of c dates only from 19 century [14]. In 1929, Edwin Hubble found that the universe is expanding [1]. As the apparent universe radius increases, the density of this latest must decrease over time, causing the refractive index of the vacuum to drop. As a result, it causes light to accelerate slowly.

In Equation (3), c is the local speed limit for light in a vacuum in our universe area. Admitting that light accelerates while the universe expands, it will tend towards another asymptotical speed limit k affected by a local refractive index n. For now, k is unknown. Let us build Equation (4), which is analog to Equation (3) for the universe [2]. Our universe parcel is at a distance r_u from the universe’s apparent mass center m_u. The local speed of light c results from Equation (4).

$c=\frac{k}{n}\text{where}n=\sqrt{\frac{1-2\Theta /k^2}{1+2\Theta /k^2}}\text{and}\Theta =\frac{-G{m}_u}{r_u}\le 0$ (4)

Similarly to r_u, the R_u value is the apparent radius of curvature of the luminous universe [6] [15] (also called Hubble radius [16] ). It is a function of c and H₀. It is “apparent” since Equation (5) assumes c constant for a time equal to the universe’s age. Now, its speed is c, but it is not constant in our model [6]. It was lower in the past and will increase while the universe expands. The H₀ value represents the expansion rate of the material universe in km·s⁻¹·MParsec⁻¹ [1]. It is the local derivative of the velocity of matter $v_m$ with respect to the element of distance dr.

$H_0={\frac{\text{d}{v}_m}{\text{d}r}|}_{r=r_u}=\frac{\beta c}{r_u}=\frac{\beta c}{\beta R_u}\Rightarrow R_u=\frac{c}{H_0}$ (5)

Locally, at a distance r = r_u, matter recedes radially from the center of mass of the universe at a rate $\beta$ times slower than the speed of light c.

$r_u=\beta R_u=\frac{\beta c}{H_0}$ (6)

The apparent mass m_u of the universe is given by Equation (7) [15] [17]:

$m_u=\frac{c^3}{G{H}_0}=\frac{R_u{c}^2}{G}$ (7)

Our universe parcel is at a distance r_u from the center of the mass m_u. It travels at a speed v_m relative to this latest. The ratio $\beta$ is the asymptotical speed of light k in a vacuum (when R_u tends towards infinity) influenced by a refractive index n that is itself influenced by a gravitational potential Θ.

$v_m=\frac{\beta k}{n}\text{where}n=\sqrt{\frac{1-2\Theta /k^2}{1+2\Theta /k^2}}\text{and}\Theta =\frac{-G{m}_u}{r_u}$ (8)

Hubble measured H₀ from the global movement of galaxies at our location [1], at r_u. They have their own movement. As the universe expands, they are generally moving away from each other. The derivative of the material universe speed v_m according to the element of distance dr evaluated at r = r_u is H₀ [6].

$H_0={\frac{\text{d}{v}_m}{\text{d}r}|}_{r=r_u}=\frac{k\beta y}{r_u}\left(\frac{1}{\left(1+y\right)\sqrt{1-y^2}}\right)\text{where}y=\frac{2G{m}_u}{k^2{r}_u}$ (9)

Solving Equations (4) to (7), and (9) gives Equations (10) to (14) [6]. The expending speed ratio $\beta$ between the material and the luminous universes is geometric. It is also the ratio between r_u and R_u. It is unique to our model and essential to depict many constants and make links between the infinitely large and small in the Dirac hypothesis on large numbers [18] [19].

$k=c\sqrt{2+\sqrt{5}}\approx 6.17\times {10}^8\text{m}\cdot {\text{s}}^{-1}$ (10)

$\beta =3-\sqrt{5}\approx 0.764$ (11)

$R_u\approx 1.28\times {10}^{26}\text{m}$ (12)

$r_u\approx 9.80\times {10}^{25}\text{m}$ (13)

$m_u\approx 1.73\times {10}^{53}\text{kg}$ (14)

3.2. Our First Method to Measure H₀ as a Function of T (from CMB)

The accuracies of m_u, r_u, and R_u widely depend on H₀ which could be between 19 and 174 km·s⁻¹·MParsec⁻¹ (listed in the software in Annex A). Therefore, a better method of measuring H₀ is required to know m_u, r_u, and R_u more accurately.

We calculated the CMB temperature T as a function of H₀ and G [6]. This equation considers the universe as an ideal black body since it would absorb any incident radiation coming from outside, and it does not reflect or transmit any form of energy outside of the luminous universe (since it expands at the speed of light).

$T=\frac{\beta }{k_b}{\left(\frac{15{\alpha }^2{h}^3{c}^5{H}_0^2}{8{\pi }^{6}G}\right)}^{1/4}$ (15)

Let us isolate H₀ from Equation (15). The accuracy mainly depends on the CMB temperature T. Using T ≈ 2.736(17) K (from Cobra probe [20] ), we get.

$H_0\left(T\right)=\frac{{\pi }^3{T}^2{k}_b^2}{{\beta }^2\alpha }\sqrt{\frac{8G}{15c^5{h}^3}}\approx 72.06\left(90\right)\text{km}\cdot {\text{s}}^{-1}\cdot {\text{MParsec}}^{-1}$ (16)

with Partridge T ≈ 2.734(10) K, and H₀ ≈ 71.95(50) km·s⁻¹·MParsec⁻¹ [21]. As the least accurate value is T, Equation (16) measures H₀ from the CMB temperature. These values lead to new links and are in our software in Annex A.

3.3. Dirac Hypothesis about Large Numbers

Dirac found (inaccurately) that large numbers come into a few orders of magnitude with same dimensions quantities ratios [18] [19]. All ratios come from N, via certain factors [22]. It represents the maximum number of photons in the universe. We get the highest number when the associated mass m_ph of a photon is the smallest. This happens when the energy of the photons is at its lowest and with a wavelength of the same length as the circumference of the luminous universe (i.e., 2πR_u) [6]. Let us calculate m_ph by equating its corpuscular and wave energies.

$m_{ph}{c}^2=\frac{hc}{2\pi R_u}\Rightarrow m_{ph}=\frac{h}{2\pi R_{u}c}\approx 2.74\times {10}^{-69}\text{kg}$ (17)

We get N by dividing the apparent mass m_u of the universe (Equation (7)) by the mass m_ph associated with a photon of 2πR_u wavelength (Equation (17)).

$N=\frac{m_u}{m_{ph}}=\frac{2\pi c^5}{hG{H}_0^2}\approx 6.3018\left(62\right)\times {10}^{121}$ (18)

If we try to make a precise evaluation of N by using the Equations (6), (7), (16), and (17), we obtain Equation (19) which is dependent mainly on T. We evaluate the result by using the CODATA 2014 [8] and the average CMB temperature from Cobra probe [20]. Finally, we note that N is dimensionless as α.

$N=\frac{15h^2{\alpha }^2{\beta }^4{c}^{10}}{4{\pi }^5{G}^2{k}_b^4{T}^4}\approx 6.31\left(15\right)\times {10}^{121}$ (19)

Assuming α used as a scale factor applied a few times, we postulate Equation (20). It seems impossible to get this equation from standard physics [2].

$\text{POSTULATE\#1:}N=1/{\alpha }^{57}\approx 6.303419702\left(84\right)\times {10}^{121}$ (20)

In the next formulas, Planck temperature is T_p ≈ 1.42 × 10³² K. This is the highest temperature reached at the Big Bang. It happens when we put the entire mass m_u in a point-like pellet of Planck length radius L_p. Planck charge is given by q_p ≈ 1.88 × 10⁻¹⁸ C.

“Large” numbers are obtained with N exponent a fraction, such as N^1/2, N^1/3, N^1/4, … N^1/57, etc. We get these in different ways by using various parameters of the universe [2]. They are always unitless. Some come from Dirac’s hypothesis on large numbers [18] [19]. Some links will be used later [6].

$N^{2/3}=\frac{m_u\alpha }{m_e{\beta }^{1/2}}=\frac{R_u^2\beta }{r_e^2}=\frac{m_p^4{\alpha }^4}{m_e^4{\beta }^2}=\frac{m_e^2\beta }{m_{ph}^2{\alpha }^2}\approx 1.58\times {10}^{81}$ (21)

$N^{1/2}=\frac{m_p}{m_{ph}}=\frac{R_u}{L_p}=\frac{1}{t_p{H}_0}=\frac{2\pi T_p{k}_b}{h{H}_0}=\frac{-1}{q_e}\sqrt{\frac{4\pi m_u{R}_u\alpha }{{\mu }_0}}\approx 7.94\times {10}^{60}$ (22)

$N^{1/3}=\frac{m_u{r}_e\alpha }{m_e{R}_u\beta }=\frac{m_e\sqrt{\beta }}{m_{ph}\alpha }=\frac{R_u\sqrt{\beta }}{r_e}=\frac{\alpha q_e^2}{4\pi {\epsilon }_{0}G\beta m_e^2}\approx 3.99\times {10}^{40}$ (23)

$N^{1/4}=\frac{T_p}{T}{\left(\frac{15{\beta }^4{\alpha }^2}{{\pi }^3}\right)}^{1/4}=\frac{k_{b}T}{m_{ph}{c}^2}{\left(\frac{{\pi }^3}{15{\beta }^4{\alpha }^2}\right)}^{1/4}\approx 2.82\times {10}^{30}$ (24)

$N^{1/6}=\frac{r_e}{L_p\sqrt{\beta }}=\frac{m_p\alpha }{m_e\sqrt{\beta }}=\frac{{\alpha }^3}{4\pi R_{\infty }{L}_p\sqrt{\beta }}=\frac{2\pi r_e{k}_b{T}_p}{hc\sqrt{\beta }}\approx 1.99\times {10}^{20}$ (25)

$N^{1/16}={\left(\frac{4\pi c{R}_{\infty }\sqrt{\beta }}{H_0}\right)}^{57/256}={\left(\frac{\beta T_p}{T}\right)}^{1/4}{\left(\frac{15{\alpha }^2}{{\pi }^3}\right)}^{1/16}\approx 4.10\times {10}^7$ (26)

$N^{1/19}=\frac{1}{4\pi R_{\infty }{r}_e}={\left(\frac{\beta m_e^2}{m_{ph}^2}\right)}^{1/12}=16{\pi }^2\beta L_p{R}_u{R}_{\infty }^2\sqrt{\alpha }\approx 2.57\times {10}^6$ (27)

$N^{1/57}=\frac{q_p^2}{q_e^2}={\left(\frac{m_p^2}{m_e^2\beta }\right)}^{1/21}={\left(\frac{q_e^2}{4\pi \beta {\epsilon }_{0}G{m}_e^2}\right)}^{1/20}=\frac{1}{\alpha }\approx \text{137}$ (28)

In a non-published document [22], we show over 150 links that give N with various parameters. The universe is well-linked between the infinitely large and the infinitely small. Almost everything changes while the universe is expanding.

3.4. Precise Calculation of H₀

Unlike Equation (16), we look for an equation that does not use G and T to get H₀ since they do not have good accuracies. Usually, G intervenes in the calculations of gravitational force and energy. Without any details (see [6] [7] ), let us calculate the electrical energy E_e between two electrons separated by a space equal to the classical electron radius r_e. The electrical energy E_e is not linked to the distance since we get $E_e=m_e{c}^2$. We evaluate the gravitational energy for the same conditions, finding $E_g=G{m}_e^2/r_e$. If these experiments are done at the luminous universe periphery, we get an electrical energy ${E^{\prime }}_e=E_e$ and a gravitational energy ${E^{\prime }}_g=E_g/\beta$. The ratio between ${E^{\prime }}_e$ and ${E^{\prime }}_g$ gives Equation (29).

$\frac{{E^{\prime }}_e}{{E^{\prime }}_g}=\frac{m_e{c}^2}{\left(\frac{G{m}_e^2\beta }{r_e}\right)}=\frac{c^2{r}_e}{G{m}_e\beta }\approx 5.45\times {10}^{42}$ (29)

As in Equation (20), we realize that the fine-structure constant α plays a role in determining orders of magnitude. By adjusting the exponent of the fine-structure constant α, we obtain a result identical to Equation (29).

$\frac{1}{{\alpha }^{20}}\approx 5.45\times {10}^{42}$ (30)

Equations (29) and (30) seam equal. By isolating G, we get an equation that becomes postulate #2. We cannot deduce this equation from standard physics.

$\begin{array}{l}\text{POSTULATE\#2:}G=\frac{c^2{r}_e{\alpha }^{20}}{m_e\beta }\approx 6.673229809\left(86\right)\times {10}^{-11}{\text{m}}^3\cdot {\text{kg}}^{-1}\cdot {\text{s}}^{-2}\\ \text{where}\beta =3-\sqrt{5}\end{array}$ (31)

We associate the wave energy with the energy of the electron mass m_e.

$m_e{c}^2=\frac{hc\alpha }{2\pi r_e}$ (32)

with Equations (20), (31), and (32), we get Equation (33).

$H_0=\frac{c{\alpha }^{19}\sqrt{\beta }}{r_e}\approx 72.09548580\left(32\right)\text{km}\cdot {\text{s}}^{-1}\cdot {\text{MParsec}}^{-1}$ (33)

This value is like Soltis with 72.1 ± 2.0 km·s⁻¹·MParsec⁻¹, Martinelli’s with $\text{72}.{\text{1}}_{-1.8}^{+2.1}$ km·s⁻¹·MParsec⁻¹, and Salvatelli’s with $\text{72}.{\text{1}}_{-2.3}^{+3.2}$ km·s⁻¹·MParsec⁻¹ (see the list of value in our software in Annex A). Our theoretical value seems to make sense.

3.5. Our Second Method to Measure H₀ as a Function of G

We want to find a second way to measure H₀ as a function of G. We must use accurate parameters, such as α and the characteristics of the electron (m_e and r_e). We look for an equation dependent on G without any rational exponent that reduces the sensitivity. We can use Equations (31) and (33). From each of them, we isolate r_e, and we make both equal to get H₀. Since G is the least precise value, Equation (34) evaluates H₀ as a function of G. We used CODATA 2014 values.

$H_0=\frac{c^3{\alpha }^{39}}{G{m}_e\sqrt{\beta }}\approx 72.086\left(36\right)\text{km}\cdot {\text{s}}^{-1}\cdot {\text{MParsec}}^{-1}$ (34)

This result is about 25 times more precise than Equation (16) that uses the average CMB temperature T. We included this result in our software in Annex A.

4. Hubble Constant versus the Age of the Universe

We calculate the universe’s age with our cosmological model to understand what seems to be two potential values of H₀. We measure H₀ by observing cosmological objects. Universe’s age Δt_u is of complex type and results from the integral of the inverse of the expanding speed of the material universe v_m with the element of distance dr evaluated between the universe’s center of mass (at r = 0) and the apparent material universe radius of curvature at our location r_u.

$\Delta t_u={\displaystyle \underset{r=0}{\overset{r=r_u}{\int }}\frac{1}{v_m\left(r\right)}\text{d}r}=\Delta t_{hu}+\Delta t_{0h}$ (35)

The Δt_hu is the time elapsed between the horizon (r = r_h) and here (r = r_u):

$\Delta t_{hu}={\displaystyle \underset{r=r_h}{\overset{r=r_u}{\int }}\frac{1}{v_m\left(r\right)}\text{d}r}\left(\text{Realtyperesult}\right)$ (36)

The Δt_0h is the elapsed time between r = 0 and the horizon r = r_h:

$\Delta t_{0h}={\displaystyle \underset{r=0}{\overset{r=r_h}{\int }}\frac{1}{v_m\left(r\right)}\text{d}r}\left(\text{Imaginarytyperesult}\right)$ (37)

At the universe horizon r = r_h, the speed of light is zero. We cannot see beyond the horizon. The delay Δt_hu is the time elapsed between the horizon h and our actual position r_u in the universe. The delay Δt_0h is the time elapsed between the center of mass of the universe and the horizon r_h (given by Equation (38)).

$r_h=\frac{2G{m}_u}{k^2}$ (38)

Performing the integral calculation of Equation (35), we get Equation (39).

$\begin{array}{l}{\displaystyle \int \frac{1}{v_m\left(r\right)}\text{d}r}=\frac{\left(z(r)+2G\cdot m_u\ln \left(2\left[k^{2}r+z\left(r\right)\right]\right)\right)}{\beta k^3}\\ \text{where}z\left(r\right)=\sqrt{k^4{r}^2-4G^2{m}_u^2}\end{array}$ (39)

We can decompose the age of the universe Δt_u into two parts, Δt_hu and Δt_0h. The value Δt_hu represents the time elapsed between r = r_h (at the horizon) and our actual position r = r_u in the universe. The value Δt_0h gives the time elapsed between r = 0 (at the Big Bang) and r = r_h (at the horizon).

$\Delta t_u=\Delta t_{hu}+\Delta t_{0h}\approx \left(9.50+10.47i\right)\times {10}^9\text{yearswhere}i=\sqrt{-1}$ (40)

The imaginary time Δt_0h means that it elapses independently of our time. We cannot see an event between r = 0 and r = r_h, and an observer located between r = 0 and r_h could not see us. The Δt_hu equation is:

$\begin{array}{l}\Delta t_{hu}=\frac{1}{H_0}\left(\frac{{\left(\omega +2\ln \left[\omega +\beta \left(2+\sqrt{5}\right)\right]-\ln \left(4\right)\right)}^2}{\sqrt{22+10\sqrt{5}}}\right)\approx \frac{7}{10H_0}\\ \text{where}\omega =\sqrt{{\beta }^2\left(9+4\sqrt{5}\right)-4}\end{array}$ (41)

The precise equation for Δt_0h is:

$\Delta t_{0h}=\frac{-\left(2+\pi \right)}{H_0\sqrt{22+10\sqrt{5}}}i\approx \frac{-77}{100H_0}i$ (42)

The modulus of the complex age Δt_u gives the universe’s apparent age T_u.

$T_u=\left|\Delta t_u\right|=\left|{\Delta }_{hu}+\Delta t_{0h}\right|=\sqrt{{\left(\Delta t_{hu}\right)}^2+{\left(\Delta t_{0h}i\right)}^2}\approx 14.14\times {10}^9\text{years}$ (43)

$T_u=\frac{1}{H_0}\underset{\eta \approx 1\left(\text{withabout4}\text{.25\%oferror}\right)}{\underset{︸}{\sqrt{{\left(\frac{{\left(\omega +2\ln \left[\omega +\beta \left(2+\sqrt{5}\right)\right]-\ln \left(4\right)\right)}^2}{\sqrt{22+10\sqrt{5}}}\right)}^2+{\left(\left[\frac{-\left(2+\pi \right)}{\sqrt{22+10\sqrt{5}}}\right]i\right)}^2}}}$ (44)

As the square root over the accolade is approximatively equal to 1, we get:

$T_u\approx \frac{1}{H_0}\approx 13.56\times {10}^9\text{years}$ (45)

The value of the correction factor between Equations (43) and (45) is η.

$\eta =H_0{T}_u=H_0\sqrt{{\left(\Delta t_{hu}\right)}^2+{\left(\Delta t_{0h}i\right)}^2}\approx 1.042516951$ (46)

This η explains why scientists currently measure two values of H₀. Scientists can only size the apparent age of the universe with different techniques. They cannot measure the real part and the imaginary part of the universe’s age.

There is no “local” or “far” value of H₀. There is only one H₀. Some techniques give H₀ directly, and others need a correction factor. There is no need for any correction factor when H₀ is calculated from Equation (33), measured with the CMB temperature with Equation (16), or with the universal gravitational constant G with Equation (34). Other techniques may get similar results than Equation (43), and if we impose that value to fit with Equation (45), we get ${H^{\prime }}_0$.

${H^{\prime }}_0=\frac{1}{\left|\Delta t_u\right|}\approx \frac{1}{14.14\times {10}^9\text{years}}\approx \frac{H_0}{\eta }\approx 69.2\text{km}\cdot {\text{s}}^{-1}\cdot {\text{MParsec}}^{-1}$ (47)

However, Equation (45) gives the actual H₀ value:

$H_0\approx \frac{1}{13.56\times {10}^9\text{years}}\approx 72.1\text{km}\cdot {\text{s}}^{-1}\cdot {\text{MParsec}}^{-1}$ (48)

If scientists could measure the real part of the universe’s age and associate this value with 1/H₀, they would obtain the following value.

$H_0\approx \frac{1}{9.50\times {10}^9\text{years}}\approx 102.94\text{km}\cdot {\text{s}}^{-1}\cdot {\text{MParsec}}^{-1}$ (49)

If scientists could measure the imaginary part somehow, the association of this value with 1/H₀ (like in Equation (45)) would give the following H₀ value.

$H_0\approx \frac{1}{10.47\times {10}^9\text{years}}\approx 93.39\text{km}\cdot {\text{s}}^{-1}\cdot {\text{MParsec}}^{-1}$ (50)

with different types of experiments to measure the apparent age of the universe, scientists usually get either ~H₀ ≈ 69.2 or ~72.1 km·s⁻¹·Mparsec⁻¹. We assume that all calibration factors are used. New techniques could require other unknown corrective factors that have nothing to do with the related phenomenon.

The articles rarely give enough details to check if the process used needs η. Scientists must verify if the η factor is required for their approach.

5. Other Experimental Measurements of Hubble Constant H₀

In 1929, Hubble made the first observational-based measurements with cepheids and got H₀ ≈ 500 km·s⁻¹·MParsec⁻¹ [1]. Sadly, even with a correct principle, his value is higher than the typical value due to errors in distance calibrations.

Let us validate our theoretical H₀ with an adequate interpretation of 508 measurements found on the Internet. The ends of their tolerance ranges give 1016 values. To find H₀ that has the highest probability to be measured, we compile the number of crossings with the tolerance ranges for each value of H₀. It generates a curve with two tips (Figure 1). The higher it is, the greater the chances are that this value of H₀ may be part of many tolerance ranges among the collected data.

A simple statistical phenomenon may be described with a Gaussian function. For fitting a wavy curve, it is necessary to make the sum of many Gaussians. A simpler model with fewer degrees of liberty must always be privileged.

A curve fit is done by summing different Gaussians (shown in Figure 2). A better gap fitting reduces the risk of finding other results. Thus, we gave a heavier weight (×10) to all data located between 69.2 and 72.1 km·s⁻¹·MParsec⁻¹ (from our theory). We tried with and without this approach, and it gives about the same result. As it improves the gap fitting, we kept this approach.

Figure 1. Number of crossings with tolerance ranges as a function of the H₀.

Figure 2. Gaussian curves used to approximate the original curve in Figure 1.

Each tip in Figure 1 is approximated in Figure 2 with two positive Gaussians. We force these curves to be around two means, even though there are four positive curves. It removes two degrees of liberty. We must add a negative Gaussian to model the gap between the two mean values. We must elaborate on this negative Gaussian. Our theory predicts “two close values” of H₀. On the curve, a deep gap shows up. It is impossible to get such a gap by only adding positives Gaussians which give two little bumps without any gap. To get a real gap, we must add a negative Gaussian. Let us see in Figure 3 what would look like a curve fit without any negative Gaussian. Since the tips are close, they mix up to build only one tip.

The Gaussian sum in Figure 3 peaks around H₀ ≈ 71.11 km·s⁻¹·MParsec⁻¹. The result is not close to our theoretical H₀ ≈ 72.09548580 km·s⁻¹·MParsec⁻¹ (Equation (33)), but it is about what is found if statistics were used through the whole data set, thinking they should see only one tip. Moreover, Jang & Lee showed a similar value of H₀ ≈ 71.17 km·s⁻¹·MParsec⁻¹ (listed in our software in Annex A) that supposedly reduces the tension between the values obtained by cepheids (calibrated on SNe Ia) and CMB.

In Figure 1, we find two groups around H₀ ≈ 69.7 and 71.8 km·s⁻¹·MParsec⁻¹. It is known that there is currently a tension between two groups [5]. A significant gap appears between the two tips. The only way to create such a gap is to

Figure 3. Approximated curve (orange tip) without negative Gaussian curves.

withdraw values nearby a specific value. It would then create a negative Gaussian, such as in Figure 2. It is delicate to debate why some values may have been withdrawn. It could be intentional or not. In the past, it was difficult to see a difference between these groups. Now, the tolerances are small enough to clearly see two groups. With recent growing tensions between these two clans, some may be inclined to shrink or shift some tolerance ranges when it overlaps with neighbor values.

In Figure 4, we apply η to the curves around H₀ ≈ 69.882 km·s⁻¹·MParsec⁻¹. Then, all curves stand around H₀ ≈ 72.36 km·s⁻¹·MParsec⁻¹. Then, with the curves of Figure 4, we build the curve in Figure 5. Figure 6 is a zoom of its tip.

We want to know the precise value of H₀ for which the derivative of the Gaussian summation is 0. It corresponds to the highest probability of getting the true H₀ value. Unfortunately, the derivative of a Gaussian summation is not an easy equation to get in a software. We rather use a numerical technic to get it. In Figure 6, we show a zoom of the quadratic curve fit around the tip value. Using the equation, we take the derivative and find its maximum. The quadratic equation has the following form:

$\begin{array}{l}y\left(x\right)=A{x}^2+Bx+C\\ \text{Atthetip,theslopeis}:y^{\prime }\left(x\right)=\frac{\text{d}x}{\text{d}y}=2Ax+B=0\to x=\frac{-B}{2A}\\ \text{where}x=H_0\text{,}y=\text{numberofcrossingswithdifferenttoleranceranges}\end{array}$ (51)

$H_0=\frac{-B}{2A}\approx \frac{2423.2459592464}{2\times 16.8057572117}\approx 72.0957088907\text{km}\cdot {\text{s}}^{-1}\cdot {\text{MParsec}}^{-1}$ (52)

This result is well centered on our theoretical value within 3 parts per million. Our approach considers that both clans are someway right. Indeed, their different approaches and results also highlight a new phenomenon. It gives credit to our theory of the universe’s complex age that predicts a few possible fake H₀ values.

We have 508 data. Each has a tolerance range (that may be symmetrical or not) that generates two H₀ values. Therefore, there are a total of i_max = 1016 data at the end. The following equation depicts the statistical error e_t:

Figure 4. Gaussian curves modified with a correction factor η.

Figure 5. Result of the summation of 4 Gaussian curves from Figure 4.

Figure 6. Zoom of the tip shown in Figure 5 + parabolic curve fit.

$e_t\approx \frac{\sqrt{{\displaystyle \underset{i=1}{\overset{i=i_{\max }}{\sum }}{e}_i^2}}}{i_{\max }}$ (53)

We mention that 16 H₀ values in our software in Annex A come from statistics. We kept them since some are mixed up with new valuable data information. So, we modify Equation (53) to remove them to reduce their impact on the total e_t error. We use the following equation where n = 2 × 16 = 32 (each data generates two H₀ values) is the number of elements to exclude from our sample. The total e_t error reduces with the square root of the number of elements included in our sample.

$e_t\approx \frac{\sqrt{{\displaystyle \underset{i=1}{\overset{i=i_{\max }}{\sum }}{e}_i^2}}}{i_{\max }}\cdot \left[\frac{\sqrt{i_{\max }}}{\sqrt{i_{\max }-n}}\right]$ (54)

If n = 0, we fall back on Equation (53). With i_max = 1016, Equation (53) gives e_t ≈ ±0.32 km·s⁻¹·MParsec⁻¹. With i_max = 1016 and n = 32, Equation (54) rounds up to e_t ± 0.33 km·s⁻¹·MParsec⁻¹. The impact of these n elements has a very little impact.

$H_0\approx 72.0957\pm 0.33\text{km}\cdot {\text{s}}^{-1}\cdot {\text{MParsec}}^{-1}$ (55)

In Annex A, we supply the software used to get this result. All the main steps enumerated in this article are clearly shown. The software uses starting values (found via Excel) to fit the original curve with 5 Gaussian curves (#0 to #4 to use the same numbers as the software). Each Gaussian uses three parameters: μ is the mean value, σ represents the variance, and m is a multiplication factor.

$f\left(H_0\right)\approx \frac{m}{\sigma \sqrt{2\pi }}{\text{e}}^{\frac{-1}{2}{\left(\frac{H_0-\mu }{\sigma }\right)}^2}$ (56)

Here are the values for the 5 Gaussian curves used to fit the original curve:

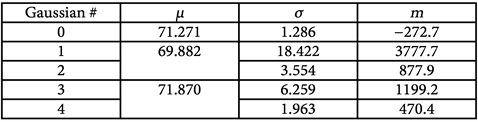(57)

For Gaussians #1 and #2, we force the software to use the same mean value. We do the same thing for Gaussians #3 and #4. We also note that the multiplication factor m of Gaussian #0 is negative. With these values, we stopped iterating when the sum of squares of errors was lower than 22000. We see in Figure 1 that the obtained approximated curve fits well the original curve. In our software (Annex A), the iterations start with values close to what they should be.

The specificity of our approach is to say that the two clans are someway right. However, we must apply a correction factor to one of them. Indirectly, it gives credit to a complex universe age that predicts a few possible fake values of H₀.

After reading this article, scientists should continue their work as they were doing, without applying any correction factor to their raw data. The correction factor should only be used on the final Gaussian curve to analyze data.

6. A Reminder of Different Useful Identities

To avoid repeating everything unnecessarily, we recall different identities that will be used later to determine H₀. Planck units are commonly defined as follows.

$\text{Planckmass}:m_p=\sqrt{\frac{hc}{2\pi G}}\approx 2.18\times {10}^{-8}\text{kg}$ (58)

$\text{Plancktime}:t_p=\sqrt{\frac{hG}{2\pi c^5}}=\frac{L_p}{c}\approx 5.91\times {10}^{-44}\text{s}$ (59)

$\text{Plancklength}:L_p=\sqrt{\frac{hG}{2\pi c^3}}=c{t}_p\approx 1.61\times {10}^{-35}\text{m}$ (60)

$\text{PlanckTemperature}:T_p=\sqrt{\frac{h{c}^3}{2\pi G{k}_b^2}}=\frac{m_p{c}^2}{k_b}\approx 1.42\times {10}^{32}\text{K}$ (61)

$\text{Planckcharge}:q_p=\sqrt{2ch{\epsilon }_0}=\frac{-q_e}{\sqrt{\alpha }}\approx 1.88\times {10}^{-18}\text{C}$ (62)

The fine-structure constant α is linked to Rydberg constant R_∞ and the electron mass m_e by the following equation:

$R_{\infty }=\frac{c{m}_e{\alpha }^2}{2h}$ (63)

The speed of light c is given as a function of μ₀ and ε₀.

$c=\frac{1}{\sqrt{{\mu }_0{\epsilon }_0}}$ (64)

Associating the mass-energy of a Planck particle with its wave energy and then, using Equations (31), (32), (64), and (62), we get Planck charge q_p defined several ways and as a function of c, G, and h like the other Planck units.

$q_p=\sqrt{\frac{2h}{c{\mu }_0}}=\sqrt{\frac{4\pi m_p{L}_p}{{\mu }_0}}=\sqrt{\frac{\beta G{h}^2}{\pi {\mu }_0{r}_e^2{c}^4{\alpha }^{19}}}$ (65)

The electron’s charge is determined from the mass of the electron m_e, the classical electron radius r_e, and the vacuum permeability μ₀.

$q_e=\sqrt{\frac{4\pi m_e{r}_e}{{\mu }_0}}\approx -1.60\times {10}^{-19}\text{C}$ (66)

Let us calculate the precise value of the average temperature T of the CMB. We first make equal Equations (16) and (33). Then, we replace G by Equation (31), and we get rid of Planck constant h by its value from Equation (32).

$T=\frac{m_e{c}^2}{k_b}{\left(\frac{15{\beta }^6{\alpha }^{17}}{{\pi }^3}\right)}^{1/4}\approx 2.7367958\left(16\right)\text{K}$ (67)

This CMB temperature is like Kimura with 2.737 K [23].

7. Different Equations to Calculate H₀

For an academic purpose and to show the interdependence of H₀ with the other “constants”, we will enumerate equations using various universe parameters. Some overcome the inherent difficulties in measuring H₀ and show a roundabout way of obtaining an accurate value of it. We also find some others which depend on interesting values, or more precise ones. Using the constants c, k_b, T, m_e, r_e, h, G, μ₀, ε₀, m_u, R_u, R_∞, q_e, q_p, t_p, l_p, T_p, m_p, m_ph, and $\beta$, we find many equations.

The H₀ parameter is not constant since 1/H₀ represents an approximation of the apparent universe’s age, and H₀ get smaller over time. Since the universe is old, H₀ changes slowly. If the constancy of all the universe’s parameters is maintained as it is currently done in metrology, the universe’s age and H₀ will seem constant.

Results of 508 different experiences reduce the error by 508^1/2 ≈ 22.5. It may look like a significant number, but it is nothing besides what has been done to measure the electron characteristics accurately. Particle accelerators use millions of electrons at each experiment, and they repeat these many times to find something new. Computers analyze the collisions’ results to make the electron’s characteristics more and more accurate. It is why there is no manner to get better results than that of Equation (33), as it is based on well-known characteristics of the electron. We will see further many other equations that give precise results.

Replacing G by Equation (31) in Equation (16), we get Equation (68).

$H_0={\pi }^3{k}_b^2{T}^2{\alpha }^9\sqrt{\frac{8r_e}{15m_e{c}^3{h}^3{\beta }^5}}$ (68)

Replacing h in Equation (68) by using Equation (32), we get Equation (69).

$H_0=k_b^2{T}^2\sqrt{\frac{{\pi }^3{\alpha }^{21}}{15r_e^2{m}_e^4{\beta }^5{c}^6}}$ (69)

Replacing h in Equation (16) by using Equation (32), we get Equation (70).

$H_0=\frac{k_b^2{T}^2}{{\beta }^2}\sqrt{\frac{{\pi }^{3}G\alpha }{15r_e^3{m}_e^3{c}^8}}$ (70)

Replacing T in Equation (70) by using Equation (67), we get Equation (71).

$H_0=\beta {\alpha }^9\sqrt{\frac{G{m}_e}{r_e^3}}$ (71)

Using Equation (32) in Equation (33), we get Equation (72).

$H_0=\frac{2\pi m_e{c}^2{\alpha }^{18}\sqrt{\beta }}{h}$ (72)

With Equations (63) and (72), we get the most accurate equation.

$H_0=4\pi c{R}_{\infty }{\alpha }^{16}\sqrt{\beta }$ (73)

Using Equation (31) in Equation (73), we get Equation (74).

$H_0=\frac{4\pi G{m}_e{R}_{\infty }{\beta }^{3/2}}{c{r}_e{\alpha }^4}$ (74)

Equation (74) gives H₀ with G₂₀₁₄ (from CODATA 2014). The measurement of H₀(G₂₀₁₄) ≈ 72.105(36) km·s⁻¹·MParsec⁻¹ is our fourth way to measure H₀.

Using Equation (63) in Equation (74), we get Equation (75). This equation is also a good candidate for measuring H₀ as a function of G.

$H_0=\frac{8\pi Gh{R}_{\infty }^2{\beta }^{3/2}}{r_e{c}^2{\alpha }^4}$ (75)

Using Equation (32) in Equation (75), we get Equation (76).

$H_0=\frac{16{\pi }^{2}G{m}_e{R}_{\infty }^2{\beta }^{3/2}}{c{\alpha }^7}$ (76)

This equation is another good candidate for measuring H₀ as a function of G. The measure still gives the same result as Equation (74).

We will enumerate other equations without making all the rather fastidious demonstrations. However, all these may be found from previous equations.

$H_0=\frac{2\pi m_{ph}{c}^2}{h}$ (77)

$H_0=2c^2\sqrt{\frac{\pi R_{\infty }{\alpha }^{55}}{G{m}_e}}$ (78)

$H_0=\beta {\alpha }^9\sqrt{\frac{m_{e}c}{r_e^3}}$ (79)

$H_0=8\beta \sqrt{G{m}_e{\left(\pi R_{\infty }\right)}^3{\alpha }^9}$ (80)

$H_0=8c\sqrt{\beta r_e{\left(\pi R_{\infty }\right)}^3{\alpha }^{29}}$ (81)

$H_0=\sqrt{\frac{2\pi c^5{\alpha }^{57}}{hG}}$ (82)

$H_0=2c\sqrt{\frac{\pi \beta R_{\infty }{\alpha }^{25}}{r_e}}$ (83)

$H_0=\sqrt{\frac{2\pi \beta m_e{c}^3{\alpha }^{37}}{h{r}_e}}$ (84)

$H_0=\frac{2{\pi }^2}{h}{\left(\frac{k_b^4{T}^4}{15m_u{\alpha }^2{c}^2{\beta }^4}\right)}^{1/3}$ (85)

$H_0=\frac{2\pi k_b{T}_p}{h}\sqrt{{\alpha }^{57}}$ (86)

$H_0=\frac{c{\mu }_0{q}_e^2{\alpha }^{19}\sqrt{\beta }}{4\pi m_e{r}_e^2}$ (87)

$H_0=\frac{q_e^2{\alpha }^{19}\sqrt{\beta }}{4\pi c{\epsilon }_0{m}_e{r}_e^2}$ (88)

$H_0=\frac{q_p^2{\alpha }^{18}\sqrt{\beta }}{2h{\epsilon }_0{r}_e}$ (89)

$H_0=\frac{c{\mu }_0{q}_p^2{\alpha }^{20}\sqrt{\beta }}{4\pi m_e{r}_e^2}$ (90)

$H_0=\frac{q_p^2{\alpha }^{20}\sqrt{\beta }}{4\pi c{\epsilon }_0{m}_e{r}_e^2}$ (91)

$H_0=\frac{c\beta q_p^2\sqrt{{\alpha }^{19}}}{4\pi {\epsilon }_0{k}_b{T}_p{r}_e^2}$ (92)

$H_0=\frac{c\beta q_e^2\sqrt{{\alpha }^{17}}}{4\pi {\epsilon }_0{k}_b{T}_p{r}_e^2}$ (93)

$H_0=\frac{c{q}_e^2{\beta }^2}{4{\epsilon }_0{k}_{b}T{r}_e^2}{\left(\frac{15{\alpha }^{97}}{{\pi }^7}\right)}^{1/4}$ (94)

$H_0=\frac{2k_{b}T}{\beta h}{\left(\frac{{\pi }^7{\alpha }^{55}}{15}\right)}^{1/4}$ (95)

$H_0=\frac{k_{b}T}{\beta r_e{m}_{e}c}{\left(\frac{{\pi }^3{\alpha }^{59}}{15}\right)}^{1/4}$ (96)

$H_0=\frac{4\pi k_{b}T}{\beta c{\mu }_0{q}_e^2}{\left(\frac{{\pi }^3{\alpha }^{59}}{15}\right)}^{1/4}$ (97)

$H_0=\frac{4\pi k_{b}T}{\beta c{\mu }_0{q}_p^2}{\left(\frac{{\pi }^3{\alpha }^{55}}{15}\right)}^{1/4}$ (98)

$H_0=\frac{G{k}_{b}T}{c^3{r}_e^2}{\left(\frac{{\pi }^3}{15{\alpha }^{21}}\right)}^{1/4}$ (99)

$H_0=\frac{2G{m}_e{k}_{b}T}{h{r}_e{c}^2}{\left(\frac{{\pi }^7}{15{\alpha }^{25}}\right)}^{1/4}$ (100)

$H_0=\frac{G{m}_p{k}_{b}T}{m_e{c}^3{r}_e^2}{\left(\frac{{\pi }^3{\alpha }^{21}}{15{\beta }^2}\right)}^{1/4}$ (101)

$H_0=\frac{G{m}_u{k}_{b}T}{m_e{c}^3{r}_e^2}{\left(\frac{{\pi }^3{\alpha }^{135}}{15{\beta }^2}\right)}^{1/4}$ (102)

$H_0=\frac{G{m}_e{k}_{b}T}{m_p{c}^3{r}_e^2}{\left(\frac{{\pi }^3{\beta }^2}{15{\alpha }^{63}}\right)}^{1/4}$ (103)

$H_0=\frac{16cG{k}_{b}T{\epsilon }_0{m}_e^2}{q_e^4}{\left(\frac{{\pi }^{11}}{15{\alpha }^{21}}\right)}^{1/4}$ (104)

$H_0=\beta m_e^2\sqrt{\frac{8{\pi }^{3}G{c}^3{\alpha }^{15}}{h^3}}$ (105)

$H_0=\frac{c^3{\alpha }^{39}}{G{m}_e\sqrt{\beta }}$ (106)

The last equation measures H₀ from G since all other constants are accurate. Many equations are excellent candidates for measuring H₀ as a function of G or T. These equations could represent valuable tools for cosmologists.

This document gives 42 equations of H₀ as a function of various universe parameters. Since H₀ may be defined using different parameters, we suggest that some of the most critical universe parameters are well linked, as much in the infinitely small as in the infinitely large, and H₀ is part of these.

8. Why Is H₀ Not Really a Constant?

We want to explain why Hubble parameter H₀ cannot be constant over time. As simple as it is, the reverse of Hubble parameter H₀ is related to the apparent age of the universe (see Equation (45)). Consequently, the H₀ parameter is changing over time. It is, therefore, by abuse of language that we call H₀ the Hubble “constant”. To be more precise, we should say the Hubble “parameter”.

When H₀ is expressed in km·s⁻¹·MParsec⁻¹, the ninth digit after the dot changes every year. It goes completely unnoticed. More than that, even if we could achieve this precision in our measurements of H₀, it would still go unnoticed since we forced c to be constant in 1983. In metrology, scientists choose the speed of light as a standard. Even though c changes every year, if we force it to be constant, we willfully readjust all other constants and units (distance, time, and mass) as a function of c to keep it constant. Then, H₀ looks constant as other parameters.

9. Conclusions

This article aimed to show that our theoretical value from Equation (33) (giving H₀ ≈ 72.09548580(32) km·s⁻¹·MParsec⁻¹) [6] is the right one, despite a growing tension [5] between values around 69.2 and 72.1 km·s⁻¹·MParsec⁻¹.

With 508 data (from [24] to [310] shown in our software in Annex A), a graph showing the actual tension [5] between two values is shown. We decomposed the curve into Gaussians. A negative one is required to explain the large gap between the two H₀ values, and it is due to withdrawn values. So, we restored them by removing that curve. Then, we applied a η ≈ 1.042516951 correction factor (from our theory) to the curves located at ~H₀ ≈ 69.2 km·s⁻¹·MParsec⁻¹. Our theory highlights a misunderstanding of the link between 1/H₀ and the universe’s apparent age. With the proper correction factor applied, we get a statistical value of H₀ ≈ 72.0957 ± 0.33 km·s⁻¹·MParsec⁻¹, which is close to our theoretical value. Our discovery of the η factor may help to reduce the tension between scientists. Someway we show that even if two H₀ values seem to be commonly found with various techniques, both are accurate if a proper correction factor is used.

With a new cosmological model, we get an apparent age of the universe of about 14.14 billion years. The exact formula is approximated from an elaborate integral result by the well-known 1/H₀ equation that gives 13.56 billion years. Different techniques may lead to either value. It depends if it is an attempt to measure the universe’s age locally or far away. There is no “local” or “distant” value of H₀, as some may pretend [46] [47]. Sticking their measurement of the apparent age of the universe to 1/H₀, most cosmologists get results that stand around 69.2 or 72.1 km·s⁻¹·MParsec⁻¹. Our hypothesis may explain the actual tension [5] relative to these two values. However, there is only one true H₀ value, and the other one is just misinterpreted as being the Hubble constant without quite being so.

Even if many theoretical equations of H₀ are shown in this article, we highlight that we also found a few interesting ways to measure the H₀ accurately using the CMB temperature T and the value of the universal gravitational constant G from CODATA 2014. These results confirm our theoretical value.

H₀ ≈ 72.06(90) km·s⁻¹·MParsec⁻¹ and 71.95(50) km·s⁻¹·MParsec⁻¹ from T,

H₀ ≈ 72.086(36) km·s⁻¹·MParsec⁻¹ and 72.105(36) km·s⁻¹·MParsec⁻¹ from G.

For an academic purpose, we enumerated 42 equations of H₀ using different parameters. These equations showed that H₀ is intricated with all other “constants”. For metrology purposes, the speed of light in a vacuum is forced to be constant to be an unchanging standard. If this situation is considered valid in a metrology context, H₀ should also be considered constant and become part of the CODATA. However, if 1/H₀ represents an approximation of the universe’s age, it would also make sense to say that H₀ is changing over time.

Einstein’s and Schwarzschild’s equations show that massive objects such as the universe influence the speed of light. As the universe expands, its density diminishes, and the local speed of light increases over time.

The fine-structure constant α is unitless and may be described as a ratio where the variation rate at the numerator counterbalances the variation rate at the denominator. Apart from α and $\beta$, all “constants” used to describe H₀ in our equations somehow emanate from fundamental units such as the meter, the second, and the kilogram. These units are now defined by the speed of light. As H₀ describes the universe’s age and depends on many unit-dependent “constants” based on c, we should consider c and all universe’s unit-dependent parameters as changing over time. Forcing c to be constant is necessary for metrology purposes, but it is not in the interest of physicists for explaining phenomena. An accurate value of H₀ has a great interest in deepening our understanding of the universe.

Annex A (C++ Software)

// This software finds "the best" experimental value of H0 with a set of 508 data

//Compiled on Dev-C++ 5.11 available for free at:

// https://sourceforge.net/projects/orwelldevcpp/

#include

#include

#include

#define printf __mingw_printf

#define nbH0 508 //Number of measurements of H0 analyzed

#define Pi 3.141592654 //Definition of Pi

double Mean[5],Sigma[5],Multiplier[5];//Caracteristics of Gaussian curves

double A,B,C; //Coefficients of the quadratic equation of the tip

double LMSTip; //Least mean square for the approximation tip curve

double BEH; //Best estimate of H0

double H0[2*nbH0-1],NbCrossings[2*nbH0-1];

double nbCrossings[2*nbH0-1]; //Vector of number of crossings

double Accuracy_ppm; //Accuracy of H0 compared to the theoretical value

double TVH = 72.09548580; //Theoretical value of H0 (in km/(s*MParsec)

unsigned int PosTipIndex; //Index corresponding to the tip of nbCrossings array

int n = 20; //Sample before & after PosTipIndex to build the tip equation

double Sqr(double value) {return value*value;} //***Returns the square value

//***Function that returns the square root value

double Sqrt(double Value) {

double D; /*Dummy value*/ double V; /*Returned value*/ int i; /*Counter*/

V=0; D=Value;

for (i=0;i<=50;i++) { //Gives 50 bits of precision

D=-D/2;

if (D<0) while (V*V>Value) V=V+D; else while (V*V

return V;

} //End of Sqrt

double Exp(double Value) { return pow(2.718281828,Value);} //***e^Value

//***This procedure creates a table of 2*nbH increasing values

//***of H0[i] with the tolerances T[i] and the signs +/- Variation[i].

void CreateTableOfCrossingH0Ranges(void) {

double PT[nbH0],NT[nbH0]; //Positive tolerance and negative tolerance

double Variation[2*nbH0]; //Variation from the tolerance range

double DH0,DSgn; //Dummy H0 and Sgn used to put H in increasing order

int DeltaCrossings; //Variation of on the number of crossings

int i,j,k; //Counters

i=0;

//We enumerate all H0 values and their tolerance range found on Internet

//In brackets, we add the bibliographic references

H0[i]=69; PT[i]=+16; NT[i++]=-8; // [24] Abbott et al.

H0[i]=70; PT[i]=+2.7; NT[i++]=-2.7; // [25] Addisson

H0[i]=72.4; PT[i]=+3.9; NT[i++]=-4.8; // [25] Addisson

H0[i]=73.1; PT[i]=+3.3; NT[i++]=-3.9; // [25] Addisson

H0[i]=73.2; PT[i]=+1.3; NT[i++]=-1.3; // [25] Addisson

H0[i]=68.7; PT[i]=+1.3; NT[i++]=-1.3; // [25] Addisson

H0[i]=73.5; PT[i]=+5.3; NT[i++]=-5.3; // [26] Baxter & Sherwin

H0[i]=73.3; PT[i]=+0.7; NT[i++]=-0.7; // [27] Blakeslee et al.

H0[i]=73.78; PT[i]=+0.84; NT[i++]=-0.84; // [28] Bonilla

H0[i]=73.577; PT[i]=+0.106; NT[i++]=-0.106; // [29] Dainotti et al.

H0[i]=73.493; PT[i]=+0.144; NT[i++]=-0.144; // [29] Dainotti et al.

H0[i]=73.222; PT[i]=+0.262; NT[i++]=-0.262; // [29] Dainotti et al.

H0[i]=73.664; PT[i]=+0.223; NT[i++]=-0.223; // [29] Dainotti et al.

H0[i]=73.576; PT[i]=+0.105; NT[i++]=-0.105; // [29] Dainotti et al.

H0[i]=73.513; PT[i]=+0.142; NT[i++]=-0.142; // [29] Dainotti et al.

H0[i]=73.192; PT[i]=+0.265; NT[i++]=-0.265; // [29] Dainotti et al.

H0[i]=73.678; PT[i]=+0.223; NT[i++]=-0.223; // [29] Dainotti et al.

H0[i]=71.8; PT[i]=+3.9; NT[i++]=-3.3; // [30] Denzel et al.

H0[i]=72.94; PT[i]=+0.75; NT[i++]=-0.75; // [31] Di Valentino

H0[i]=72.7; PT[i]=+1.1; NT[i++]=-1.1; // [31] Di Valentino

H0[i]=68.8; PT[i]=+45.7; NT[i++]=-25.5; // [32] Gayathri et al.

H0[i]=62.3; PT[i]=+9.1; NT[i++]=-9.1; // [33] Hagstotz et al.

H0[i]=70.5; PT[i]=+2.37; NT[i++]=-2.37; // [34] Kethan et al.

H0[i]=72.86; PT[i]=+0.036; NT[i++]=-0.036; //Mercier (this document)

H0[i]=72.105; PT[i]=+0.036; NT[i++]=-0.036; //Mercier (this document)

H0[i]=68.3; PT[i]=+4.6; NT[i++]=-4.6; // [35] Mukherjee et al.

H0[i]=70; PT[i]=+0.5; NT[i++]=-0.5; // [36] Park et al.

H0[i]=65.1; PT[i]=+3; NT[i++]=-5.4; // [37] Philcox et al.

H0[i]=65.6; PT[i]=+3.4; NT[i++]=-3.5; // [37] Philcox et al.

H0[i]=70.6; PT[i]=+3.7; NT[i++]=-5; // [37] Philcox et al.

H0[i]=78.3; PT[i]=+2.9; NT[i++]=-2.9; // [38] Qi et al.

H0[i]=73.6; PT[i]=+1.8; NT[i++]=-1.6; // [38] Qi et al.

H0[i]=73; PT[i]=+1.4; NT[i++]=-1.4; // [39] Riess et al.

H0[i]=73.2; PT[i]=+1.3; NT[i++]=-1.3; // [39] Riess et al.

H0[i]=72.1; PT[i]=+2; NT[i++]=-2; // [40] Soltis et al.

H0[i]=69.5; PT[i]=+4; NT[i++]=-4; // [41] Wang & Giannios

H0[i]=71; PT[i]=+20; NT[i++]=-20; // [42] Zhang et al.

H0[i]=67.4; PT[i]=+0.5; NT[i++]=-0.5; // [43] Aghanim et al.

H0[i]=67.73; PT[i]=+0.41; NT[i++]=-0.41; // [44] Benevento

H0[i]=68.22; PT[i]=+0.39; NT[i++]=-0.39; // [44] Benevento

H0[i]=72.5; PT[i]=+1.85; NT[i++]=-1.85; // [44] Benevento

H0[i]=69.17; PT[i]=+1.09; NT[i++]=-1.09; // [44] Benevento

H0[i]=74.5; PT[i]=+5.6; NT[i++]=-6.1; // [45] Birrer et al.

H0[i]=67.4; PT[i]=+4.1; NT[i++]=-3.2; // [45] Birrer et al.

H0[i]=75.35; PT[i]=+1.68; NT[i++]=-1.68; // [46] Camarena & Marra

H0[i]=74; PT[i]=+0.625; NT[i++]=-0.625; // [47] Chang & Zhu

H0[i]=73.8; PT[i]=+6.3; NT[i++]=-5.8; // [48] Coughlin et al.

H0[i]=71.2; PT[i]=+3.2; NT[i++]=-3.1; // [48] Coughlin et al.

H0[i]=72.4; PT[i]=+1.4; NT[i++]=-1.4; // [49] D'Agostino

H0[i]=71.5; PT[i]=+1.3; NT[i++]=-1.3; // [49] D'Agostino

H0[i]=71.54; PT[i]=+1.78; NT[i++]=-1.78; // [50] Dai WM et al.

H0[i]=73.12; PT[i]=+1.14; NT[i++]=-1.14; // [50] Dai WM et al.

H0[i]=66.2; PT[i]=+4.4; NT[i++]=-4.2; // [51] Dietrich et al.

H0[i]=69.9; PT[i]=+0.84; NT[i++]=-0.86; // [52] Gonzalez et al.

H0[i]=71; PT[i]=+4; NT[i++]=-4; // [53] González-Serrena et al.

H0[i]=74.62; PT[i]=+12.35; NT[i++]=-11.34; // [54] Haboury

H0[i]=71.89; PT[i]=+11.02; NT[i++]=-10.17; // [54] Haboury

H0[i]=76.44; PT[i]=+55.76; NT[i++]=-50.17; // [54] Haboury

H0[i]=50.9; PT[i]=+31.1; NT[i++]=-31.9; // [54] Haboury

H0[i]=50.81; PT[i]=+28.19; NT[i++]=-27.81; // [54] Haboury

H0[i]=71; PT[i]=+2; NT[i++]=-3; // [55] Harvey

H0[i]=65.9; PT[i]=+1.5; NT[i++]=-1.5; // [56] Holanda et al.

H0[i]=65.9; PT[i]=+4.4; NT[i++]=-4; // [56] Holanda et al.

H0[i]=64.3; PT[i]=+4.5; NT[i++]=-4.4; // [56] Holanda et al.

H0[i]=66.8; PT[i]=+13.4; NT[i++]=-9.2; // [57] Howlett & Davis

H0[i]=64.8; PT[i]=+7.3; NT[i++]=-7.2; // [57] Howlett & Davis

H0[i]=75.8; PT[i]=+5.2; NT[i++]=-4.9; // [58] Jaeger et al.

H0[i]=65.8; PT[i]=+3.5; NT[i++]=-3.5; // [59] Kim et al.

H0[i]=72.3; PT[i]=+1.4; NT[i++]=-1.4; // [60] Kreisch et al.

H0[i]=71.5; PT[i]=+11.9; NT[i++]=-10.6; // [61] Li & Zhang

H0[i]=74.7; PT[i]=+5.8; NT[i++]=-5.8; // [62] Lombriser

H0[i]=72.06; PT[i]=+0.09; NT[i++]=-0.09; // [7] Mercier

H0[i]=74; PT[i]=+1.6; NT[i++]=-1.6; // [63] Millon et al.

H0[i]=74.2; PT[i]=+1.7; NT[i++]=-1.8; // [63] Millon et al.

H0[i]=50.4; PT[i]=+28.1; NT[i++]=-19.5; // [64] Mukherjee et al.

H0[i]=62.2; PT[i]=+29.5; NT[i++]=-19.7; // [64] Mukherjee et al.

H0[i]=43.1; PT[i]=+24.6; NT[i++]=-11.4; // [64] Mukherjee et al.

H0[i]=67.6; PT[i]=+4.3; NT[i++]=-4.2; // [64] Mukherjee et al.

H0[i]=68.6; PT[i]=+14; NT[i++]=-8.5; // [65] Nicolaou et al.

H0[i]=69.6; PT[i]=+1; NT[i++]=-1.3; // [66] Niedermann and Sloth

H0[i]=71.4; PT[i]=+1; NT[i++]=-1; // [66] Niedermann and Sloth

H0[i]=72; PT[i]=+12; NT[i++]=-8.2; // [67] Palmese et al.

H0[i]=69.03; PT[i]=+0.87; NT[i++]=-0.87; // [68] Pandey et al.

H0[i]=70.6; PT[i]=+1.1; NT[i++]=-1.1; // [68] Pandey et al.

H0[i]=68.44; PT[i]=+0.52; NT[i++]=-0.52; // [68] Pandey et al.

H0[i]=68.1; PT[i]=+0.58; NT[i++]=-0.58; // [68] Pandey et al.

H0[i]=73.9; PT[i]=+3; NT[i++]=-3; // [69] Pesce et al.

H0[i]=68.6; PT[i]=+1.8; NT[i++]=-1.8; // [70] Pogosian et al.

H0[i]=74.03; PT[i]=+1.42; NT[i++]=-1.42; // [71] Rui-Yun et al.

H0[i]=75.1; PT[i]=+2.3; NT[i++]=-2.3; // [72] Schombert et al.

H0[i]=74.2; PT[i]=+2.7; NT[i++]=-3; // [73] Shajib et al.

H0[i]=67.52; PT[i]=+0.96; NT[i++]=-0.95; // [74] Sharov & Sinyakov

H0[i]=70.87; PT[i]=+1.63; NT[i++]=-1.62; // [74] Sharov & Sinyakov

H0[i]=69; PT[i]=+29; NT[i++]=-14; // [75] Vasylyev & Filippenko

H0[i]=67; PT[i]=+41; NT[i++]=-26; // [75] Vasylyev & Filippenko

H0[i]=71; PT[i]=+34; NT[i++]=-30; // [75] Vasylyev & Filippenko

H0[i]=70; PT[i]=+29; NT[i++]=-18; // [75] Vasylyev & Filippenko

H0[i]=72.3; PT[i]=+2.9; NT[i++]=-2.8; // [76] Vogl

H0[i]=75.3; PT[i]=+3; NT[i++]=-2.9; // [77] Wei & Melia

H0[i]=75.3; PT[i]=+1.9; NT[i++]=-1.9; // [77] Wei & Melia

H0[i]=67.9; PT[i]=+1.1; NT[i++]=-1.3; // [78] Wu et al.

H0[i]=72; PT[i]=+2.1; NT[i++]=-2.5; // [78] Wu et al.

H0[i]=73.65; PT[i]=+1.95; NT[i++]=-2.26; // [79] Yang et al.

H0[i]=67.95; PT[i]=+0.78; NT[i++]=-1.03; // [80] Zhang & Huang

H0[i]=69.81; PT[i]=+2.22; NT[i++]=-2.7; // [80] Zhang & Huang

H0[i]=66.75; PT[i]=+3.42; NT[i++]=-4.23; // [80] Zhang & Huang

H0[i]=70.75; PT[i]=+1.55; NT[i++]=-1.55; // [81] Agrawal

H0[i]=73.7; PT[i]=+1.4; NT[i++]=-1.4; // [82] Anderson

H0[i]=72.5; PT[i]=+2.1; NT[i++]=-2.3; // [83] Birrer

H0[i]=67.4; PT[i]=+0.5; NT[i++]=-0.5; // [84] Chang et al.

H0[i]=82.8; PT[i]=+9.4; NT[i++]=-8.3; // [85] Chen et al.

H0[i]=70.1; PT[i]=+5.3; NT[i++]=-4.5; // [85] Chen et al.

H0[i]=77; PT[i]=+4; NT[i++]=-4.6; // [85] Chen et al.

H0[i]=75.6; PT[i]=+3.2; NT[i++]=-3; // [85] Chen et al.

H0[i]=76.8; PT[i]=+2.6; NT[i++]=-2.6; // [85] Chen et al.

H0[i]=75.7; PT[i]=+4.5; NT[i++]=-4.4; // [86] Collett

H0[i]=76.8; PT[i]=+4.2; NT[i++]=-3.8; // [86] Collett

H0[i]=74.2; PT[i]=+3; NT[i++]=-2.9; // [86] Collett

H0[i]=67.6; PT[i]=+1.1; NT[i++]=-1.1; // [87] Cuceu et al.

H0[i]=67.4; PT[i]=+6; NT[i++]=-6.2; // [88] Domínguez

H0[i]=66.6; PT[i]=+1.6; NT[i++]=-1.6; // [88] Domínguez

H0[i]=70.3; PT[i]=+1.36; NT[i++]=-1.35; // [89] Dutta et al.

H0[i]=77; PT[i]=+37; NT[i++]=-18; // [90] Fishbach et al.

H0[i]=76; PT[i]=+19; NT[i++]=-13; // [90] Fishbach et al.

H0[i]=69.8; PT[i]=+0.8; NT[i++]=-0.8; // [91] Freedman et al.

H0[i]=68.09; PT[i]=+0.45; NT[i++]=-0.45; // [92] Guo et al.

H0[i]=69.34; PT[i]=+0.93; NT[i++]=-0.93; // [92] Guo et al.

H0[i]=69.67; PT[i]=+0.95; NT[i++]=-0.94; // [92] Guo et al.

H0[i]=69.36; PT[i]=+0.82; NT[i++]=-0.82; // [92] Guo et al.

H0[i]=69.25; PT[i]=+0.99; NT[i++]=-0.99; // [92] Guo et al.

H0[i]=74; PT[i]=+16; NT[i++]=-8; // [93] Hotokezaka et al.

H0[i]=70.3; PT[i]=+5.3; NT[i++]=-5; // [93] Hotokesaka et al.

H0[i]=82.4; PT[i]=+8.4; NT[i++]=-8.3; // [94] Jee et al.

H0[i]=67; PT[i]=+3; NT[i++]=-3; // [95] Kozmanyan et al.

H0[i]=72.2; PT[i]=+2.1; NT[i++]=-2.1; // [96] Liao et al.

H0[i]=73; PT[i]=+2.8; NT[i++]=-3; // [96] Liao et al.

H0[i]=67.8; PT[i]=+1.3; NT[i++]=-1.3; // [97] MacAulay et al.

H0[i]=67.37; PT[i]=+0.62; NT[i++]=-0.62; // [98] Martinelli

H0[i]=68.8; PT[i]=+1.6; NT[i++]=-1.6; // [98] Martinelli

H0[i]=73.9; PT[i]=+2.5; NT[i++]=-2.5; // [98] Martinelli

H0[i]=67.68; PT[i]=+0.46; NT[i++]=-0.46; // [98] Martinelli

H0[i]=68.4; PT[i]=+1; NT[i++]=-1; // [98] Martinelli

H0[i]=69.2; PT[i]=+1.5; NT[i++]=-1.5; // [98] Martinelli

H0[i]=67.51; PT[i]=+0.61; NT[i++]=-0.61; // [98] Martinelli

H0[i]=68.9; PT[i]=+1.1; NT[i++]=-1.1; // [98] Martinelli

H0[i]=72.1; PT[i]=+2.1; NT[i++]=-1.8; // [98] Martinelli

H0[i]=67.75; PT[i]=+0.46; NT[i++]=-0.46; // [98] Martinelli

H0[i]=68.59; PT[i]=+0.86; NT[i++]=-0.86; // [98] Martinelli

H0[i]=69.6; PT[i]=+1.3; NT[i++]=-1.3; // [98] Martinelli

H0[i]=71.505; PT[i]=+0.03; NT[i++]=-0.03; // [2] Mercier

H0[i]=69; PT[i]=+1.7; NT[i++]=-1.7; // [99] Park & Ratra

H0[i]=69.8; PT[i]=+1.8; NT[i++]=-1.8; // [99] Park & Ratra

H0[i]=68.9; PT[i]=+1.7; NT[i++]=-1.7; // [99] Park & Ratra

H0[i]=70.1; PT[i]=+1.9; NT[i++]=-1.9; // [99] Park & Ratra

H0[i]=68.5; PT[i]=+1.8; NT[i++]=-1.8; // [99] Park & Ratra

H0[i]=69.6; PT[i]=+1.9; NT[i++]=-1.9; // [99] Park & Ratra

H0[i]=72; PT[i]=+1.9; NT[i++]=-1.9; // [100] Reid

H0[i]=73.5; PT[i]=+1.4; NT[i++]=-1.4; // [100] Reid

H0[i]=74.22; PT[i]=+1.82; NT[i++]=-1.82; // [101] Riess et al.

H0[i]=74.03; PT[i]=+1.42; NT[i++]=-1.42; // [101] Riess et al.

H0[i]=72.8; PT[i]=+1.1; NT[i++]=-1.1; // [102] Riess

H0[i]=74.3; PT[i]=+1; NT[i++]=-1; // [102] Riess

H0[i]=71.6; PT[i]=+3.8; NT[i++]=-4.9; // [103] Rusu et al.

H0[i]=67.99; PT[i]=+0.91; NT[i++]=-0.88; // [104] Ryan

H0[i]=68.24; PT[i]=+2.39; NT[i++]=-2.33; // [104] Ryan

H0[i]=66.79; PT[i]=+2.6; NT[i++]=-2.32; // [104] Ryan

H0[i]=66.8; PT[i]=+2.5; NT[i++]=-2.3; // [104] Ryan

H0[i]=66.13; PT[i]=+1.38; NT[i++]=-2.09; // [104] Ryan

H0[i]=67.1; PT[i]=+2.4; NT[i++]=-2.3; // [104] Ryan

H0[i]=68.44; PT[i]=+0.7; NT[i++]=-0.69; // [104] Ryan

H0[i]=69.32; PT[i]=+1.42; NT[i++]=-1.42; // [104] Ryan

H0[i]=68; PT[i]=+2.27; NT[i++]=-1.94; // [104] Ryan

H0[i]=66.6; PT[i]=+2.2; NT[i++]=-1.9; // [104] Ryan

H0[i]=67.19; PT[i]=+1; NT[i++]=-1.6; // [104] Ryan

H0[i]=66.8; PT[i]=+1.8; NT[i++]=-1.7; // [104] Ryan

H0[i]=63.13; PT[i]=+6.48; NT[i++]=-6.48; // [105] Saha & Sahoo

H0[i]=74.2; PT[i]=+2.7; NT[i++]=-3; // [106] Shajib et al.

H0[i]=75; PT[i]=+40; NT[i++]=-32; // [107] Soares-Santos

H0[i]=78; PT[i]=+96; NT[i++]=-24; // [107] Soares-Santos

H0[i]=73.1; PT[i]=+0.7; NT[i++]=-0.7; // [108] Taubenberger et al.

H0[i]=68; PT[i]=+14; NT[i++]=-7; // [109] Tiwari et al.

H0[i]=68; PT[i]=+18; NT[i++]=-8; // [109] Tiwari et al.

H0[i]=73.9; PT[i]=+1; NT[i++]=-1; // [110] Verde et al.

H0[i]=72.5; PT[i]=+1.2; NT[i++]=-1.2; // [110] Verde et al.

H0[i]=73.3; PT[i]=+1.7; NT[i++]=-1.8; // [111] Wong et al.

H0[i]=72.4; PT[i]=+2; NT[i++]=-2; // [112] Yuan et al.

H0[i]=68.36; PT[i]=+0.53; NT[i++]=-0.52; // [113] Zhang & Huang

H0[i]=64.9; PT[i]=+4.6; NT[i++]=-4.3; // [114] Zeng and Yan

H0[i]=67.4; PT[i]=+1.1; NT[i++]=-1.2; // [115] Abbott et al.

H0[i]=69.3; PT[i]=+0.4; NT[i++]=-0.6; // [115] Abbott et al.

H0[i]=73.24; PT[i]=+1.74; NT[i++]=-1.74; // [116] Benetti et al.

H0[i]=72.5; PT[i]=+2.1; NT[i++]=-2.1; // [117] Bolejko

H0[i]=68.1; PT[i]=+2; NT[i++]=-2; // [117] Bolejko

H0[i]=76; PT[i]=+8; NT[i++]=-8; // [118] Braatz

H0[i]=69.3; PT[i]=+4.2; NT[i++]=-4.2; // [118] Braatz

H0[i]=71.9; PT[i]=+7.1; NT[i++]=-7.1; // [119] Cantiello et al.

H0[i]=73.24; PT[i]=+1.74; NT[i++]=-1.74; // [120] Chen

H0[i]=67.4; PT[i]=+0.5; NT[i++]=-0.5; // [120] Chen

H0[i]=73.24; PT[i]=+1.74; NT[i++]=-1.74; // [121] Choudhury & Choubey

H0[i]=72.8; PT[i]=+1.6; NT[i++]=-1.6; // [122] Dhawan et al.

H0[i]=55; PT[i]=+7; NT[i++]=-20;// [123] Di Valentino & Melchiorri

H0[i]=67.06; PT[i]=+1.68; NT[i++]=-1.68; // [124] Gomez-Valent

H0[i]=68.9; PT[i]=+1.96; NT[i++]=-1.96; // [124] Gomez-Valent

H0[i]=68.45; PT[i]=+2; NT[i++]=-2; // [124] Gomez-Valent

H0[i]=73.5; PT[i]=+4.6; NT[i++]=-4.7; // [125] Grillo

H0[i]=72.8; PT[i]=+4.3; NT[i++]=-4.1; // [125] Grillo

H0[i]=69.8; PT[i]=+5.3; NT[i++]=-4.1; // [125] Grillo

H0[i]=70.38; PT[i]=+0.6; NT[i++]=-0.6; // [126] Hoeneisen et al.

H0[i]=71.17; PT[i]=+1.66; NT[i++]=-1.66; // [127] Lee & Jang

H0[i]=73.52; PT[i]=+1.62; NT[i++]=-1.62; // [128] Riess et al.

H0[i]=73.83; PT[i]=+1.48; NT[i++]=-1.48; // [128] Riess et al.

H0[i]=73.48; PT[i]=+1.66; NT[i++]=-1.66; // [129] Riess et al.

H0[i]=74.4; PT[i]=+4.9; NT[i++]=-4.9; // [130] Van Putten

H0[i]=74.5; PT[i]=+7.3; NT[i++]=-7.3; // [130] Van Putten

H0[i]=74.9; PT[i]=+2.6; NT[i++]=-2.6; // [130] Van Putten

H0[i]=66.8; PT[i]=+1.9; NT[i++]=-1.9; // [130] Van Putten

H0[i]=73.75; PT[i]=+1.44; NT[i++]=-1.44; // [130] Van Putten

H0[i]=70; PT[i]=+12; NT[i++]=-8; // [131] Vitale

H0[i]=67; PT[i]=+4; NT[i++]=-4; // [132] Yu et al.

H0[i]=67.498; PT[i]=+7.97; NT[i++]=-3.278; // [133] Zhang

H0[i]=70; PT[i]=+12; NT[i++]=-8; // [134] Abbott

H0[i]=72.5; PT[i]=+2.5; NT[i++]=-8; // [135] Bethapudi & Desai

H0[i]=71.9; PT[i]=+2.4; NT[i++]=-3; // [136] Bonvin et al.

H0[i]=69.2; PT[i]=+1.4; NT[i++]=-2.2; // [136] Bonvin et al.

H0[i]=79; PT[i]=+4.4; NT[i++]=-4.2; // [136] Bonvin et al.

H0[i]=73.75; PT[i]=+2.11; NT[i++]=-2.11; // [137] Cardona

H0[i]=67.81; PT[i]=+0.92; NT[i++]=-0.92; // [137] Cardona

H0[i]=66.93; PT[i]=+0.62; NT[i++]=-0.62; // [137] Cardona

H0[i]=73.46; PT[i]=+1.4; NT[i++]=-1.4; // [137] Cardona

H0[i]=68.3; PT[i]=+2.7; NT[i++]=-2.6; // [138] Chen Yun et al.

H0[i]=68.4; PT[i]=+2.9; NT[i++]=-3.3; // [138] Chen Yun et al.

H0[i]=65; PT[i]=+6.6; NT[i++]=-6.6; // [138] Chen Yun et al.

H0[i]=67.9; PT[i]=+2.4; NT[i++]=-2.4; // [138] Chen Yun et al.

H0[i]=68; PT[i]=+2.8; NT[i++]=-2.8; // [139] Farooq

H0[i]=73.24; PT[i]=+1.74; NT[i++]=-1.74; // [139] Farooq

H0[i]=72.72; PT[i]=+1.67; NT[i++]=-1.67; // [140] Feeney et al.

H0[i]=73.15; PT[i]=+1.78; NT[i++]=-1.78; // [140] Feeney et al.

H0[i]=67.6; PT[i]=+0.7; NT[i++]=-0.6; // [141] Grieb et al.

H0[i]=73; PT[i]=+1.75; NT[i++]=-1.75; // [142] Guo & Zhang

H0[i]=73.24; PT[i]=+1.74; NT[i++]=-1.74; // [143] Hjorth et al.

H0[i]=69.13; PT[i]=+0.24; NT[i++]=-0.24; // [144] Huang and Huang

H0[i]=71.66; PT[i]=+1.8; NT[i++]=-1.8; // [145] Jang & Lee

H0[i]=73.72; PT[i]=+2.03; NT[i++]=-2.03; // [145] Jang & Lee

H0[i]=71.17; PT[i]=+1.66; NT[i++]=-1.66; // [145] Jang & Lee

H0[i]=66.2; PT[i]=+8.9; NT[i++]=-8.9; // [146] Pritychenko

H0[i]=67.2; PT[i]=+6.9; NT[i++]=-6.9; // [146] Pritychenko

H0[i]=69.13; PT[i]=+2.34; NT[i++]=-2.34; // [147] Wang et al.

H0[i]=73.24; PT[i]=+1.74; NT[i++]=-1.74; // [148] Wei & Wu

H0[i]=69.6; PT[i]=+0.7; NT[i++]=-0.7; // [148] Wei & Wu

H0[i]=73.1; PT[i]=+5.7; NT[i++]=-6; // [149] Wong et al.

H0[i]=72.5; PT[i]=+3.1; NT[i++]=-3.1; // [150] Zhang et al.

H0[i]=67.8; PT[i]=+0.9; NT[i++]=-0.9; // [151] Ade et al.

H0[i]=66; PT[i]=+6; NT[i++]=-6; // [152] Gao et al.

H0[i]=70.1; PT[i]=+0.34; NT[i++]=-0.34; // [153] Ichiki et al.

H0[i]=66.5; PT[i]=+1.8; NT[i++]=-1.8; // [154] Ludovic et al.

H0[i]=64.2; PT[i]=+1.9; NT[i++]=-1.9; // [154] Ludovic et al.

H0[i]=91.8; PT[i]=+5.3; NT[i++]=-5.3; // [155] Moresco et al.

H0[i]=72.25; PT[i]=+2.51; NT[i++]=-2.51; // [156] Riess et al.

H0[i]=72.04; PT[i]=+2.67; NT[i++]=-2.67; // [156] Riess et al.

H0[i]=76.18; PT[i]=+2.37; NT[i++]=-2.37; // [156] Riess et al.

H0[i]=74.5; PT[i]=+3.27; NT[i++]=-3.27; // [156] Riess et al.

H0[i]=73.24; PT[i]=+1.74; NT[i++]=-1.74; // [156] Riess et al.

H0[i]=76.2; PT[i]=+3.4; NT[i++]=-3.4; // [157] Tully et al.

H0[i]=75; PT[i]=+2; NT[i++]=-2; // [157] Tully et al.

H0[i]=68.17; PT[i]=+1.55; NT[i++]=-1.56; // [158] Cheng & Qing Guo

H0[i]=68.11; PT[i]=+1.69; NT[i++]=-1.69; // [158] Cheng & Qing Guo

H0[i]=68.11; PT[i]=+0.86; NT[i++]=-0.86; // [158] Cheng & Qing Guo

H0[i]=67.7; PT[i]=+1.1; NT[i++]=-1.1; // [159] Cuesta et al.

H0[i]=69.8; PT[i]=+2.6; NT[i++]=-2.6; // [160] Jang & Lee

H0[i]=72.2; PT[i]=+3.3; NT[i++]=-3.3; // [160] Jang & Lee

H0[i]=68.1; PT[i]=+5.9; NT[i++]=-5.9; // [161] Kumar et al.

H0[i]=73; PT[i]=+26; NT[i++]=-22; // [162] Kuo et al.

H0[i]=70.6; PT[i]=+2.6; NT[i++]=-2.6; // [163] Rigault et al.

H0[i]=68.8; PT[i]=+3.3; NT[i++]=-3.3; // [163] Rigault et al.

H0[i]=67.3; PT[i]=+1.2; NT[i++]=-1.2; // [164] Ade et al.

H0[i]=70.8; PT[i]=+2.4; NT[i++]=-2.4; // [165] Ben-Dayan et al.

H0[i]=69.6; PT[i]=+0.7; NT[i++]=-0.7; // [166] Bennett et al.

H0[i]=64.9; PT[i]=+4.2; NT[i++]=-4.2; // [167] Busti et al.

H0[i]=72.5; PT[i]=+2.5; NT[i++]=-2.5; // [168] Efstathiou

H0[i]=70.6; PT[i]=+3.3; NT[i++]=-3.3; // [168] Efstathiou

H0[i]=74.1; PT[i]=+2.2; NT[i++]=-2.2; // [169] Lima & Cunha

H0[i]=70; PT[i]=+2.2; NT[i++]=-2.2; // [170] Bennett et al.

H0[i]=69.32; PT[i]=+0.8; NT[i++]=-0.8; // [170] Bennett et al.

H0[i]=68; PT[i]=+4.8; NT[i++]=-4.8; // [171] Braatz et al.

H0[i]=68; PT[i]=+2.8; NT[i++]=-2.8; // [172] Farooq & Bathra

H0[i]=73.8; PT[i]=+2.4; NT[i++]=-2.4; // [172] Farooq & Bathra

H0[i]=69.7; PT[i]=+2.4; NT[i++]=-2.4; // [173] Hinshaw et al.

H0[i]=70.4; PT[i]=+2.5; NT[i++]=-2.5; // [173] Hinshaw et al.

H0[i]=69.33; PT[i]=+0.88; NT[i++]=-0.88; // [173] Hinshaw et al.

H0[i]=70.2; PT[i]=+1.4; NT[i++]=-1.4; // [173] Hinshaw et al.

H0[i]=70; PT[i]=+3; NT[i++]=-3; // [174] Humphreys et al.

H0[i]=68; PT[i]=+9; NT[i++]=-9; // [175] Kuo et al.

H0[i]=49.97; PT[i]=+0.19; NT[i++]=-0.19; // [176] Pietrzynski et al.

H0[i]=68.9; PT[i]=+7.1; NT[i++]=-7.1; // [177] Reid et al.

H0[i]=72.1; PT[i]=+3.2; NT[i++]=-2.3; // [178] Salvatelli et al.

H0[i]=74.1; PT[i]=+2.1; NT[i++]=-2.1; // [179] Scowcroft et al.

H0[i]=69; PT[i]=+6; NT[i++]=-6; // [180] Sereno and Pacificz

H0[i]=80; PT[i]=+5.8; NT[i++]=-5.7; // [181] Suyu et al.

H0[i]=75.2; PT[i]=+4.4; NT[i++]=-4.2; // [181] Suyu et al.

H0[i]=73.1; PT[i]=+2.4; NT[i++]=-3.6; // [181] Suyu et al.

H0[i]=74.4; PT[i]=+3; NT[i++]=-3; // [182] Tully et al.

H0[i]=71.3; PT[i]=+2; NT[i++]=-2; // [183] Xia et al.

H0[i]=73.8; PT[i]=+2.4; NT[i++]=-2.4; // [184] Calabrese et al.

H0[i]=68; PT[i]=+2.8; NT[i++]=-2.8; // [184] Calabrese et al.

H0[i]=69.7; PT[i]=+2.5; NT[i++]=-2.5; // [184] Calabrese et al.

H0[i]=74.3; PT[i]=+3.1; NT[i++]=-3.1; // [185] Chavez

H0[i]=67; PT[i]=+3.2; NT[i++]=-3.2; // [186] Colless et al.

H0[i]=74.3; PT[i]=+3; NT[i++]=-3; // [187] Freedman et al.

H0[i]=70.2; PT[i]=+0.14; NT[i++]=-0.14; // [188] Pozzo

H0[i]=75.4; PT[i]=+2.9; NT[i++]=-2.9; // [189] Riess et al.

H0[i]=56; PT[i]=+2; NT[i++]=-2; // [190] Wang

H0[i]=68; PT[i]=+5.5; NT[i++]=-5.5; // [191] Chen & Ratra

H0[i]=67; PT[i]=+3.2; NT[i++]=-3.2; // [192] Beutler et al.

H0[i]=71; PT[i]=+2.5; NT[i++]=-2.5; // [193] Jarosik et al.

H0[i]=70.4; PT[i]=+1.3; NT[i++]=-1.4; // [193] Jarosik et al.

H0[i]=74.8; PT[i]=+3.1; NT[i++]=-3.1; // [194] Riess et al.

H0[i]=74.4; PT[i]=+2.5; NT[i++]=-2.5; // [194] Riess et al.

H0[i]=73.8; PT[i]=+2.4; NT[i++]=-2.4; // [194] Riess et al.

H0[i]=73; PT[i]=+2; NT[i++]=-2; // [195] Freedman & Madore

H0[i]=66; PT[i]=+6; NT[i++]=-4; // [196] Paraficz et Hjorth

H0[i]=76; PT[i]=+3; NT[i++]=-3; // [196] Paraficz et Hjorth

H0[i]=70.6; PT[i]=+3.1; NT[i++]=-3.1; // [197] Suyu et al.

H0[i]=69.7; PT[i]=+4.9; NT[i++]=-5; // [197] Suyu et al.

H0[i]=70.5; PT[i]=+1.3; NT[i++]=-1.3; // [198] Hinshaw et al.

H0[i]=71.9; PT[i]=+2.6; NT[i++]=-2.7; // [198] Hinshaw et al.

H0[i]=70.5; PT[i]=+1.3; NT[i++]=-1.3; // [199] Komatsu et al.

H0[i]=70.4; PT[i]=+1.4; NT[i++]=-1.4; // [199] Komatsu et al.

H0[i]=70.9; PT[i]=+1.3; NT[i++]=-1.3; // [199] Komatsu et al.

H0[i]=70.1; PT[i]=+1.3; NT[i++]=-1.3; // [199] Komatsu et al.

H0[i]=74.2; PT[i]=+3.6; NT[i++]=-3.6; // [200] Riess et al.

H0[i]=84.2; PT[i]=+6; NT[i++]=-6; // [201] Russell

H0[i]=83.4; PT[i]=+8; NT[i++]=-8; // [201] Russell

H0[i]=88; PT[i]=+6; NT[i++]=-6; // [201] Russell

H0[i]=61.7; PT[i]=+1.2; NT[i++]=-1.1; // [202] Leith et al.

H0[i]=67; PT[i]=+13; NT[i++]=-10; // [203] Vuissoz et al.

H0[i]=63; PT[i]=+7; NT[i++]=-3; // [203] Vuissoz et al.

H0[i]=70; PT[i]=+6; NT[i++]=-6; // [204] Oguri

H0[i]=68; PT[i]=+6; NT[i++]=-6; // [204] Oguri

H0[i]=73.5; PT[i]=+3.2; NT[i++]=-3.2; // [205] Spergel et al.

H0[i]=73.2; PT[i]=+3.1; NT[i++]=-3.2; // [205] Spergel et al.

H0[i]=70.4; PT[i]=+1.5; NT[i++]=-1.6; // [205] Spergel et al.

H0[i]=76.9; PT[i]=+3.9; NT[i++]=-3.4; // [206] Bonamente et al.

H0[i]=73.7; PT[i]=+4.6; NT[i++]=-3.8; // [206] Bonamente et al.

H0[i]=77.6; PT[i]=+4.8; NT[i++]=-4.3; // [206] Bonamente et al.

H0[i]=70.8; PT[i]=+1.9; NT[i++]=-1.8; // [207] Hütsi

H0[i]=74.92; PT[i]=+2.28; NT[i++]=-2.28; // [208] Ngeow and Kanbur

H0[i]=74.37; PT[i]=+2.27; NT[i++]=-2.27; // [208] Ngeow and Kanbur

H0[i]=62.3; PT[i]=+1.3; NT[i++]=-1.3; // [209] Sandage et al.

H0[i]=60.9; PT[i]=+1.3; NT[i++]=-1.3; // [209] Sandage et al.

H0[i]=60.7; PT[i]=+1.5; NT[i++]=-1.5; // [209] Sandage et al.

H0[i]=72; PT[i]=+6; NT[i++]=-6; // [210] Wang et al.

H0[i]=73.2; PT[i]=+7; NT[i++]=-7; // [211] Gibson & Brook

H0[i]=75; PT[i]=+7; NT[i++]=-7; // [212] Hamuy

H0[i]=65; PT[i]=+12; NT[i++]=-12; // [212] Hamuy

H0[i]=58; PT[i]=+2; NT[i++]=-2; // [213] Magain

H0[i]=58; PT[i]=+2; NT[i++]=-2; // [214] Olivares et al.

H0[i]=73; PT[i]=+4; NT[i++]=-4; // [215] Riess

H0[i]=69; PT[i]=+8; NT[i++]=-8; // [216] Schmidt et al.

H0[i]=66; PT[i]=+8; NT[i++]=-8; // [217] Stritzinger et al.

H0[i]=78; PT[i]=+9; NT[i++]=-9; // [217] Stritzinger et al.

H0[i]=67; PT[i]=+30; NT[i++]=-18; // [218] Udomprasert et al.

H0[i]=64; PT[i]=+7; NT[i++]=-4; // [219] Boffi & Riess

H0[i]=33; PT[i]=+5; NT[i++]=-5; // [220] Dumin

H0[i]=69; PT[i]=+12; NT[i++]=-12; // [221] Jimenez et al.

H0[i]=75; PT[i]=+7; NT[i++]=-6; // [222] Koopmans

H0[i]=70; PT[i]=+7; NT[i++]=-7; // [223] Mei et al.

H0[i]=68; PT[i]=+6; NT[i++]=-6; // [223] Mei et al.

H0[i]=68; PT[i]=+5; NT[i++]=-5; // [223] Mei et al.

H0[i]=71; PT[i]=+4; NT[i++]=-4; // [223] Mei et al.

H0[i]=77; PT[i]=+19; NT[i++]=-15; // [224] Saunders et al.

H0[i]=85; PT[i]=+20; NT[i++]=-17; // [224] Saunders et al.

H0[i]=72; PT[i]=+5; NT[i++]=-5; // [225] Spergel et al.

H0[i]=71; PT[i]=+4; NT[i++]=-3; // [225] Spergel et al.

H0[i]=63; PT[i]=+2; NT[i++]=-2; // [226] Fassnacht et al.

H0[i]=72; PT[i]=+8; NT[i++]=-8; // [227] Freedman

H0[i]=57; PT[i]=+23; NT[i++]=-16; // [228] Grainge et al.

H0[i]=48; PT[i]=+7; NT[i++]=-4; // [229] Kochanek

H0[i]=71; PT[i]=+6; NT[i++]=-6; // [229] Kochanek

H0[i]=72; PT[i]=+8; NT[i++]=-8; // [229] Kochanek

H0[i]=62; PT[i]=+7; NT[i++]=-7; // [229] Kochanek

H0[i]=75; PT[i]=+8; NT[i++]=-8;// [230] Tikhonov & Galazoutdinova

H0[i]=81; PT[i]=+5; NT[i++]=-5;// [230] Tikhonov & Galazoutdinova

H0[i]=59; PT[i]=+15; NT[i++]=-10; // [231] Treu & Koopmans

H0[i]=71; PT[i]=+2; NT[i++]=-2; // [232] Freedman et al.

H0[i]=71; PT[i]=+3; NT[i++]=-3; // [232] Freedman et al.

H0[i]=70; PT[i]=+5; NT[i++]=-5; // [232] Freedman et al.

H0[i]=72; PT[i]=+9; NT[i++]=-9; // [232] Freedman et al.

H0[i]=82; PT[i]=+6; NT[i++]=-6; // [232] Freedman et al.

H0[i]=72; PT[i]=+8; NT[i++]=-8; // [232] Freedman et al.

H0[i]=65; PT[i]=+5; NT[i++]=-5; // [233] Itoh

H0[i]=76; PT[i]=+1.3; NT[i++]=-1.3; // [234] Jensen et al.

H0[i]=72; PT[i]=+2.3; NT[i++]=-2.3; // [234] Jensen et al.

H0[i]=65; PT[i]=+5; NT[i++]=-5; // [235] Koopmans et al.

H0[i]=71; PT[i]=+8; NT[i++]=-8; // [236] Liu & Graham

H0[i]=64; PT[i]=+14; NT[i++]=-18; // [237] Mason et al.

H0[i]=66; PT[i]=+14; NT[i++]=-11; // [237] Mason et al.

H0[i]=70; PT[i]=+7; NT[i++]=-7; // [238] Mei et al.

H0[i]=69; PT[i]=+4; NT[i++]=-4; // [239] Tonry

H0[i]=71; PT[i]=+6; NT[i++]=-6; // [240] Willick & Puneet

H0[i]=63; PT[i]=+4.3; NT[i++]=-4.3; // [241] Xiao-Feng et al.

H0[i]=69; PT[i]=+4; NT[i++]=-4; // [242] Ferrarese et al.

H0[i]=68; PT[i]=+2; NT[i++]=-2; // [243] Gibson et al.

H0[i]=71; PT[i]=+6; NT[i++]=-6; // [244] Mould et al.

H0[i]=68; PT[i]=+6; NT[i++]=-6; // [244] Mould et al.

H0[i]=71; PT[i]=+4; NT[i++]=-4; // [245] Sakai et al.

H0[i]=77; PT[i]=+7; NT[i++]=-7; // [246] Tikhonov et al.

H0[i]=69; PT[i]=+12; NT[i++]=-19; // [247] Biggs et al.

H0[i]=69; PT[i]=+18; NT[i++]=-12; // [248] Chae KH

H0[i]=74; PT[i]=+18; NT[i++]=-17; // [248] Chae KH

H0[i]=42; PT[i]=+9; NT[i++]=-9; // [249] Collier et al.

H0[i]=73; PT[i]=+6; NT[i++]=-6; // [250] Freedman et al.

H0[i]=64; PT[i]=+8; NT[i++]=-6; // [251] Jha et al.

H0[i]=85; PT[i]=+27; NT[i++]=-23; // [252] Mason & Myers

H0[i]=61; PT[i]=+15; NT[i++]=-14; // [252] Mason & Myers

H0[i]=61; PT[i]=+23; NT[i++]=-21; // [252] Mason & Myers

H0[i]=80; PT[i]=+19; NT[i++]=-17; // [252] Mason & Myers

H0[i]=68; PT[i]=+21; NT[i++]=-19; // [252] Mason & Myers

H0[i]=71; PT[i]=+5; NT[i++]=-5; // [252] Mason & Myers

H0[i]=86; PT[i]=+24; NT[i++]=-24; // [253] Mazumdar & Narasimba

H0[i]=67; PT[i]=+7; NT[i++]=-7; // [254] Tanvir et al.

H0[i]=62.9; PT[i]=+1.6; NT[i++]=-1.6; // [255] Tripp & Branch

H0[i]=62; PT[i]=+2; NT[i++]=-2; // [255] Tripp & Branch

H0[i]=60; PT[i]=+10; NT[i++]=-10; // [256] Branch

H0[i]=66; PT[i]=+15; NT[i++]=-14; // [257] Goicoechea et al.

H0[i]=77; PT[i]=+8; NT[i++]=-8; // [258] Harris et al.

H0[i]=47; PT[i]=+23; NT[i++]=-15; // [259] Hughes & Birkinshaw

H0[i]=82; PT[i]=+8; NT[i++]=-8; // [260] Lauer et al.

H0[i]=89; PT[i]=+10; NT[i++]=-10; // [260] Lauer et al.

H0[i]=65.2; PT[i]=+1.3; NT[i++]=-1.3; // [261] Riess et al.

H0[i]=63.8; PT[i]=+1.3; NT[i++]=-1.3; // [261] Riess et al.

H0[i]=55; PT[i]=+8; NT[i++]=-8; // [262] Tammann & Labhardt

H0[i]=60; PT[i]=+6; NT[i++]=-6; // [263] Tripp

H0[i]=70; PT[i]=+5; NT[i++]=-5; // [264] Giovanelli

H0[i]=76; PT[i]=+8; NT[i++]=-8; // [264] Giovanelli

H0[i]=67; PT[i]=+8; NT[i++]=-8; // [264] Giovanelli

H0[i]=75; PT[i]=+6; NT[i++]=-6; // [265] Gregg

H0[i]=67; PT[i]=+8; NT[i++]=-8; // [266] Hjorth & Tanvir

H0[i]=70; PT[i]=+7; NT[i++]=-7; // [266] Hjorth & Tanvir

H0[i]=60; PT[i]=+40; NT[i++]=-23; // [267] Holzapfel et al.

H0[i]=78; PT[i]=+34; NT[i++]=-28; // [267] Holzapfel et al.

H0[i]=78; PT[i]=+60; NT[i++]=-40; // [267] Holzapfel et al.

H0[i]=58; PT[i]=+10; NT[i++]=-5; // [268] Hoyle et al.

H0[i]=74; PT[i]=+10; NT[i++]=-10; // [269] Schechter

H0[i]=52.5; PT[i]=+2.5; NT[i++]=-2.5; // [270] Sciama

H0[i]=54.8; PT[i]=+0.3; NT[i++]=-0.3; // [270] Sciama

H0[i]=81; PT[i]=+6; NT[i++]=-6; // [271] Tonry et al.

H0[i]=69; PT[i]=+8; NT[i++]=-8; // [272] Amendola

H0[i]=80; PT[i]=+17; NT[i++]=-17; // [272] Amendola

H0[i]=49.5; PT[i]=+4.5; NT[i++]=-4.5; // [273] Biesiada

H0[i]=65; PT[i]=+8; NT[i++]=-8; // [274] Forbes et al.

H0[i]=103; PT[i]=+59; NT[i++]=-28; // [275] Kobayashi

H0[i]=82; PT[i]=+56; NT[i++]=-24; // [275] Kobayashi

H0[i]=60; PT[i]=+24; NT[i++]=-13; // [275] Kobayashi

H0[i]=51; PT[i]=+10; NT[i++]=-7; // [275] Kobayashi

H0[i]=33; PT[i]=+22; NT[i++]=-9; // [275] Kobayashi

H0[i]=74; PT[i]=+26; NT[i++]=-15; // [275] Kobayashi

H0[i]=63; PT[i]=+28; NT[i++]=-15; // [275] Kobayashi

H0[i]=80; PT[i]=+17; NT[i++]=-17; // [276] Mallik

H0[i]=87; PT[i]=+7; NT[i++]=-7; // [276] Mallik

H0[i]=55; PT[i]=+3; NT[i++]=-3; // [277] Schaefer

H0[i]=56; PT[i]=+3; NT[i++]=-3; // [277] Schaefer

H0[i]=82.5; PT[i]=+5.9; NT[i++]=-3; // [278] Grogin & Narayan

H0[i]=82.5; PT[i]=+8.7; NT[i++]=-5.6; // [278] Grogin & Narayan

H0[i]=71; PT[i]=+30; NT[i++]=-25; // [279] Herbig

H0[i]=74.6; PT[i]=+47; NT[i++]=-33; // [280] Holzapfel et al.

H0[i]=38; PT[i]=+18; NT[i++]=-16; // [281] Jones

H0[i]=80; PT[i]=+17; NT[i++]=-17; // [282] Kennicutt Jr et al.

H0[i]=73; PT[i]=+11; NT[i++]=-11; // [283] Mould

H0[i]=81; PT[i]=+11; NT[i++]=-11; // [283] Mould

H0[i]=84; PT[i]=+16; NT[i++]=-16; // [283] Mould

H0[i]=76; PT[i]=+10; NT[i++]=-10; // [283] Mould

H0[i]=82; PT[i]=+11; NT[i++]=-11; // [283] Mould

H0[i]=71; PT[i]=+10; NT[i++]=-10; // [283] Mould

H0[i]=80; PT[i]=+17; NT[i++]=-17; // [283] Mould

H0[i]=80; PT[i]=+17; NT[i++]=-17; // [284] Nakamura & Suto

H0[i]=58; PT[i]=+6; NT[i++]=-6; // [285] Rephaeli

H0[i]=51; PT[i]=+7; NT[i++]=-7; // [286] Schaefer

H0[i]=61; PT[i]=+12; NT[i++]=-12; // [286] Schaefer

H0[i]=26; PT[i]=+5; NT[i++]=-5; // [286] Schaefer

H0[i]=69; PT[i]=+8; NT[i++]=-8; // [287] Tanvir et al.

H0[i]=78; PT[i]=+11; NT[i++]=-11; // [288] Whitmore & Schweizer

H0[i]=65; PT[i]=+25; NT[i++]=-25; // [289] Birkinshaw & Hughes

H0[i]=55; PT[i]=+17; NT[i++]=-17; // [289] Birkinshaw & Hughes

H0[i]=80; PT[i]=+17; NT[i++]=-17; // [290] Freedman

H0[i]=84; PT[i]=+5; NT[i++]=-5; // [291] Lu et al.

H0[i]=73; PT[i]=+6; NT[i++]=-6; // [292] Schmidt & Kirshner

H0[i]=90; PT[i]=+10; NT[i++]=-10; // [293] Tully

H0[i]=43.5; PT[i]=+2.7; NT[i++]=-2.7; // [294] Duemmler

H0[i]=77; PT[i]=+8; NT[i++]=-8; // [295] Lauer & Postman

H0[i]=51; PT[i]=+5; NT[i++]=-5; // [295] Lauer & Postman

H0[i]=75; PT[i]=+30; NT[i++]=-30; // [296] Leibundgut & Pinto

H0[i]=40; PT[i]=+9; NT[i++]=-9; // [297] Birkinshaw

H0[i]=45; PT[i]=+12; NT[i++]=-12; // [297] Birkinshaw

H0[i]=82; PT[i]=+7; NT[i++]=-7; // [298] Tonry

H0[i]=52; PT[i]=+2; NT[i++]=-2; // [299] Sandage & Tammann

H0[i]=45; PT[i]=+3; NT[i++]=-3; // [299] Sandage & Tammann

H0[i]=73; PT[i]=+10; NT[i++]=-10; // [300] Visvanathan

H0[i]=50; PT[i]=+10; NT[i++]=-10; // [301] Sandage & Tammann

H0[i]=52; PT[i]=+2; NT[i++]=-2; // [301] Sandage & Tammann

H0[i]=50; PT[i]=+7; NT[i++]=-7; // [301] Sandage & Tammann

H0[i]=67; PT[i]=+10; NT[i++]=-10; // [302] Dressler

H0[i]=74.3; PT[i]=+11; NT[i++]=-11; // [304] Visvanathan

H0[i]=74.3; PT[i]=+11; NT[i++]=-11; // [305] Hanes

H0[i]=76; PT[i]=+8; NT[i++]=-8; // [306] Bottinelli & Gouguenheim

H0[i]=50.3; PT[i]=+4.3; NT[i++]=-4.3; // [307] Sandage & Tammann

H0[i]=56.9; PT[i]=+3.4; NT[i++]=-3.4; // [308] Sandage & Tammann

H0[i]=57; PT[i]=+6; NT[i++]=-6; // [309] Sandage & Tammann

H0[i]=55.5; PT[i]=+8.7; NT[i]=-8.7; // [310] Sandage & Tammann

//Creates an H0 array that contains all the extremities of the tolerance ranges

for (i=0;i<=nbH0-1;i++) {

H0[i+nbH0]=H0[i]+PT[i]; Variation[i+nbH0]=PT[i];

H0[i]=H0[i]+NT[i]; Variation[i]=NT[i]; }

//Sorts H0 array in ascending order with corresponding Variation of tolerance

for (j=0;j<=2*nbH0-2;j++) {

for (i=j+1;i<=2*nbH0-1;i++) {

if (H0[i]

DH0=H0[j]; DSgn=Variation[j]; H0[j]=H0[i];

Variation[j]=Variation[i]; H0[i]=DH0; Variation[i]=DSgn; } } }

for (i=0;i<=2*nbH0-1;i++) { //Builds the nbCrossings array

if (i==0) { nbCrossings[i]=1; }

else {

if (Variation[i]<0) {nbCrossings[i]=nbCrossings[i-1]+1;}

if (Variation[i]>0) {nbCrossings[i]=nbCrossings[i-1]-1;}

if (H0[i]==H0[i-1]) {

j=i; DeltaCrossings=0;

do {

if (Variation[j]<0) {DeltaCrossings=DeltaCrossings+1;}

if (Variation[j]>0) {DeltaCrossings=DeltaCrossings-1;}

j=j-1; } while (H0[j]==H0[i]);

for(k=i;k>j;k--) {nbCrossings[k]=nbCrossings[j]+DeltaCrossings;}

} } } } //End of CreateTableOfCrossingH0Ranges

//***Function that returns the y coordinate corresponding to x for non

//***centered Gaussian curve

double GaussianCurve(double x, double Mean, double Sigma, double Multiplier) {

double y; //Coordinate y corresponding to x for a non centered Gaussian

y=(Multiplier/(Sigma*Sqrt(2*Pi)))*exp(-0.5*Sqr((x-Mean)/Sigma));

return y; } //End of CreateApproximativeCurve

//***These are the best Gaussians to fit the nbCrossing array as a function of H0***

double FindsGaussianCurvesLS(double Mean[5],double Sigma[5], double Multiplier[5]) {

int i,j; /*Counters*/ double LS = 0; //Least square

double Sum; //Sum of the 5 Gaussien curve for a specific H0 value

for (j=0;j<=2*nbH0-1;j++) {

Sum=0;

for (i=0;i<=4;i++) {

Sum=Sum+GaussianCurve(H0[j],Mean[i],Sigma[i],Multiplier[i]); }

//We give a heavier weight to any error between 69.2 and 72.1 to

// model the gap between these values

if ((H0[i]>=69.2)&&(H0[i]<=72.1)) {

LS=LS+10*(Sqr(nbCrossings[j]-Sum));}

else { LS=LS+Sqr(nbCrossings[j]-Sum); }

} return LS; } //End of FindsGaussianCurvesLS

//***This function finds the best Gaussians to fit the real curve

void FindsBestGaussiansToFitRealCurve(void) {

int i; //Counter

double DMean[5],DSigma[5],DMultiplier[5]; //Dummy arrays

double LS, PLS; //Least Square and Previous Least Square

double StepMean = 0.1, StepSigma = 0.1, StepMultiplier = 0.1; //Variations

int nbMeanNotImproved = 0; //Tells how many times not improved

int nbSigmaNotImproved = 0; //Tells how many times not improved

int nbMultiplierNotImproved = 0; //Tells how many times not improved

//Starting values (approximative values only)

Mean[0]=71; Sigma[0]=1; Multiplier[0]=-280;

Mean[1]=68; Sigma[1]=17; Multiplier[1]=3800;

Mean[2]=Mean[1]; Sigma[2]=3; Multiplier[2]=880;

Mean[3]=73; Sigma[3]=7; Multiplier[3]=1200;

Mean[4]=Mean[3]; Sigma[4]=2; Multiplier[4]=470;

//Fills the 3 dummy arrays DMean, DSigma and DMultiplier

//with the same values than the arrays Mean, Sigma and Multiplier

for(i=0;i<=4;i++) {

DMean[i]=Mean[i]; DSigma[i]=Sigma[i]; DMultiplier[i]=Multiplier[i]; }

//Tries to find the 5 best Gaussians to fit the curve

do {

for (i=0;i<=4;i++) {

//We improve Mean[i], but we force

//Mean[2] = Mean[1] & Mean[4] = Mean[3]

if ((i!=2)&&(i!=4)) {

PLS=FindsGaussianCurvesLS(Mean,Sigma,Multiplier);

DMean[i]=Mean[i]+StepMean;

if (i==1) {DMean[2]=DMean[i];}

if (i==3) {DMean[4]=DMean[i];}

LS=FindsGaussianCurvesLS(DMean,DSigma,DMultiplier);

if (LS

Mean[i]=DMean[i];

if (i==1) {Mean[2]=DMean[i];}

if (i==3) {Mean[4]=DMean[i];}

nbMeanNotImproved=0; }

else {

DMean[i]=Mean[i]-StepMean;

if (i==1) {DMean[2]=DMean[i];}

if (i==3) {DMean[4]=DMean[i];}

LS=FindsGaussianCurvesLS(DMean,DSigma,DMultiplier);

if (LS

Mean[i]=DMean[i];

if (i==1) {Mean[2]=DMean[i];}

if (i==3) {Mean[4]=DMean[i];}

nbMeanNotImproved=0; }

else {

DMean[i]=Mean[i];

if (i==1) {DMean[2]=DMean[i];}

if (i==3) {DMean[4]=DMean[i];}

nbMeanNotImproved++;

if (nbMeanNotImproved>=100) {

nbMeanNotImproved=0; StepMean=StepMean/10; } } } }

//We try to improve Sigma[i]

PLS=FindsGaussianCurvesLS(Mean,Sigma,Multiplier);

DSigma[i]=Sigma[i]+StepSigma;

LS=FindsGaussianCurvesLS(DMean,DSigma,DMultiplier);

if (LS

else {

DSigma[i]=Sigma[i]-StepSigma;

LS=FindsGaussianCurvesLS(DMean,DSigma,DMultiplier);

if (LS

Sigma[i]=DSigma[i]; nbSigmaNotImproved=0; }

else {

DSigma[i]=Sigma[i]; nbSigmaNotImproved++;

if (nbSigmaNotImproved>=100) {

nbSigmaNotImproved=0; StepSigma=StepSigma/10; } } }

//We try to improve Multiplier[i]

PLS=FindsGaussianCurvesLS(Mean,Sigma,Multiplier);

DMultiplier[i]=Multiplier[i]+StepMultiplier;

LS=FindsGaussianCurvesLS(DMean,DSigma,DMultiplier);

if (LS

Multiplier[i]=DMultiplier[i]; nbMultiplierNotImproved=0; }

else {

DMultiplier[i]=Multiplier[i]-StepMultiplier;

LS=FindsGaussianCurvesLS(DMean,DSigma,DMultiplier);

if (LS

Multiplier[i]=DMultiplier[i]; nbMultiplierNotImproved=0; }

else {

DMultiplier[i]=Multiplier[i]; nbMultiplierNotImproved++;

if (nbMultiplierNotImproved>=100) {

nbMultiplierNotImproved=0;

StepMultiplier=StepMultiplier/10; } } } }

LS=FindsGaussianCurvesLS(DMean,DSigma,DMultiplier);

} while (LS>=22000); //Sets a stop point

for(i=0;i<=4;i++) {

printf("\n Mean[%i]=%10lf Sigma[%i]=%10lf Multiplier[%i]=%10lf",

i,Mean[i],i,Sigma[i],i,Multiplier[i]);

} } //End of FindsBestGaussiansToFitRealCurve

//***The function begins by shifting Mean[1] and Mean[2] of the two

//***Gaussian curves that are around H0=69.2km/(s*MParsec) to

//***H0=72.1km/(s*MParsec) with a theoretical factor of 1.042516951. Then

//***the function that modifies the global H0 array builds the summation of

//***the 4 positive Gaussian curves.

void CreatesFinalGaussianCurve(void) {

int i; //Dummy index value

//We shift Mean[1] and Mean[2] with a theoretical factor of 1.042516951

Mean[1]=Mean[1]*1.042516951; Mean[2]=Mean[1];

//We omit i=0 to remove the negative Gaussian curve

for(i=1;i<=nbH0*2-1;i++) {

nbCrossings[i]=GaussianCurve(H0[i],Mean[1],Sigma[1],Multiplier[1]);

nbCrossings[i]=nbCrossings[i]+GaussianCurve(H0[i],Mean[2],Sigma[2],

Multiplier[2]);

nbCrossings[i]=nbCrossings[i]+GaussianCurve(H0[i],Mean[3],Sigma[3],

Multiplier[3]);

nbCrossings[i]=nbCrossings[i]+GaussianCurve(H0[i],Mean[4],Sigma[4],

Multiplier[4]); } } //End of CreatesFinalGaussianCurve

//***Returns the Least Mean Square of the equation DA*x^2+DB*x+DC.

double FindsLMS(double DA, double DB, double DC) {

int i; /*Dummy index value*/ double LMS = 0; //Least Mean Square

for(i=PosTipIndex-n;i<=PosTipIndex+n;i++){

LMS=LMS+Sqr(nbCrossings[i]-(DA*H0[i]*H0[i]+DB*H0[i]+DC));

} return LMS; } //End of FindsLMS

//***Returns A, B, and C coefficients of the quadratic equation of the tip

void ApproximatesTipEquation(void) {

double LMSTipMin; //Reminds the lowest value of least mean square

double PLMSTip, NLMSTip; //LMSTip for a forward and backward step

double DA,DB,DC; //Dummy values of A, B and C coefficients

double StepA,StepB,StepC; //Step variation of the coefficients

double nbCrossingsMax = 0; //Maximum number crossings at the tip

double xa,xb,xc,ya,yb,yc; /*3 coordinates*/ int i; //Dummy index value

for(i=0;i<=nbH0*2-1;i++) { //Finds the index of the approximated tip

if (nbCrossings[i]>nbCrossingsMax) {

nbCrossingsMax=nbCrossings[i]; PosTipIndex=i; } }

i=PosTipIndex; xa=H0[i-n]; xb=H0[i]; xc=H0[i+n];

ya=nbCrossings[i-n]; yb=nbCrossings[i]; yc=nbCrossings[i+n];

//Sets coefficients ABC

A=((yc-ya)/((xc-xa)*(xc-xb)))-((yb-ya)/((xb-xa)*(xc-xb)));

B=((yb-ya)/(xb-xa))-A*(xb+xa); C=ya-A*xa*xa-B*xa; DA=A;DB=B;DC=C;

} //End of ApproximatesTipEquation

//***Function that returns the Best estimate of H0

void BestEstimateOfH0(void) {

CreateTableOfCrossingH0Ranges(); FindsBestGaussiansToFitRealCurve();

CreatesFinalGaussianCurve(); ApproximatesTipEquation();

BEH=-B/(2*A); Accuracy_ppm = (BEH-TVH)/(TVH*1E-6);

LMSTip=FindsLMS(A,B,C); } //End of BesEstimateOfH0

int main(void) {

BestEstimateOfH0();

printf("\n\n Equation of the tip: y = %.10lfx^2+ %.10lfx+ %.10lf",A,B,C);

printf("\n Best estimate of H0 = %.10lf km/(s*MParsec)",BEH);

printf("\n Theoretical H0 = %.10lf km/(s*MParsec)",TVH);

printf("\n Relative accuracy versus theoretical value = %.10lf ppm",

Accuracy_ppm);

getchar(); return 0;

} //End of main

Conflicts of Interest

The author claims that he has no conflict of interest in connection with the pub-lication of this article.

References

[1]	Hubble, E. (1929) Proceedings of the National Academy of Sciences of the United States of America, 15, 168-1973. https://doi.org/10.1073/pnas.15.3.168
[2]	Einstein, A. (1916) Annalen der Physik, 354, 769-822. https://doi.org/10.1002/andp.19163540702
[3]	Friedman, A. (1922) Zeitschrift für Physics, 10, 377-386. https://doi.org/10.1007/BF01332580
[4]	Lemaître, G. (1927) Annales de la Société Scientifique de Bruxelles, A47, 49-59. Partially Translated in English: Lemaître, G. (1931) Monthly Notices of the Royal Astronomical Society, 91, 483-490.
[5]	Verde, L., Treu, T. and Riess, A.G. (2019) Nature Astronomy, 3, 891-895. https://doi.org/10.1038/s41550-019-0902-0
[6]	Mercier, C. (2019) Journal of Modern Physics, 10, 641-662. https://doi.org/10.4236/jmp.2019.106046
[7]	Mercier, C. (2020) Journal of Modern Physics, 11, 1428-1465. https://doi.org/10.4236/jmp.2020.119089
[8]	Mohr, P.J., Newell, D.B. and Taylor, B.N. (2016) Review of Modern Physics, 88, Article ID: 035009. https://doi.org/10.1103/RevModPhys.88.035009
[9]	Jenkins, A., Villard, R. and Riess, A (2018) Hubblesite. https://stsci-opo.org/STScI-01EVSQXZ976ZY1QKQX17XJ7P5H.pdf
[10]	Einstein, A. (1905) Annalen der Physik, 322, 891-921. https://doi.org/10.1002/andp.19053221004
[11]	Einstein, A. (1911) Annalen der Physik, 340, 898-908. https://doi.org/10.1002/andp.19113401005
[12]	Grøn, Ø. (2016) American Journal of Physics, 84, 537-541. https://doi.org/10.1119/1.4944031
[13]	Binney, J. and Merrifield, M. (1998) Galactic Astronomy. Princeton University Press, Princeton, 816 p. https://press.princeton.edu/titles/6358.html
[14]	Mulligan, J.F. (1976) American Journal of Physics, 44, 960-969. https://doi.org/10.1119/1.10241
[15]	Mercier, C. (2019) Journal of Modern Physics, 10, 980-1001. https://doi.org/10.4236/jmp.2019.108065
[16]	Zichichi, A. (2000) Proceedings of the International School of Subnuclear Physics, 36, 1-708.
[17]	Carvalho, J.C. (1995) International Journal of Theoretical Physics, 34, 2507-2509. https://doi.org/10.1007/BF00670782
[18]	Dirac, P.A.M. (1938) Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 165, 199-208. https://doi.org/10.1098/rspa.1938.0053
[19]	Dirac, P.A.M. (1974) Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 338, 439-446. https://doi.org/10.1098/rspa.1974.0095
[20]	Gush, H.P. (1981) Physical Review Letters, 47, 745-748. https://doi.org/10.1103/PhysRevLett.47.745
[21]	Partridge, R.B. (1997) An Introduction to the Cosmic Microwave Background Radiation. From Quantum Fluctuations to Cosmological Structures: Proceedings of the 1st Moroccan School of Astrophysics, Casablanca, 1-10 December 1996, 141-184.
[22]	Mercier, C. (2016) More than a Hundred Ways to Get the Large Number N. Not Published. http://pragtec.com/physique/index_en.html
[23]	Kimura, K., Hashimoto, M., Sakoda, K. and Sakoda, K. (2001) The Astrophysical Journal, 561, L19-L22. https://doi.org/10.1086/324569
[24]	Abbott, B.P., et al. (2021) The Astrophysical Journal, 909, Article No. 218. https://doi.org/10.3847/1538-4357/abdcb7
[25]	Addison, G.E. (2021) The Astrophysical Journal, 912, Article No. L1. https://doi.org/10.3847/2041-8213/abf56e
[26]	Baxter, E.J. and Sherwin, B.D. (2021) Monthly Notices of the Royal Astronomical Society, 501, 1023-1035. https://doi.org/10.1093/mnras/staa3706
[27]	Blakeslee, J.P., Jensen, J.B., Ma, C.-P., Milne, P.A. and Greene, J.E. (2021) The Astrophysical Journal, 911, Article No. 65. https://doi.org/10.3847/1538-4357/abe86a
[28]	Bonilla, A., Kumar, S. and Nunes, R.C. (2021) The European Physical Journal C, 81, Article No. 127. https://doi.org/10.1140/epjc/s10052-021-08925-z
[29]	Dainotti, M.G., et al. (2021) The Astrophysical Journal, 912, Article No. 150. https://doi.org/10.3847/1538-4357/abeb73
[30]	Denzel, P., Coles, J.P., Saha, P. and Williams, L.L.R. (2021) Monthly Notices of the Royal Astronomical Society, 501, 784-801. https://doi.org/10.1093/mnras/staa3603
[31]	Di Valentino, E. (2021) Monthly Notices of the Royal Astronomical Society, 502, 2065-2073. https://doi.org/10.1093/mnras/stab187
[32]	Gayathri, V., et al. (2021) The Astrophysical Journal Letters, 908, Article No. L34. https://doi.org/10.3847/2041-8213/abe388
[33]	Hagstotz, S., Reischke, R. and Lilow R (2021) A New Measurement of the Hubble Constant Using Fast Radio Bursts. arXiv:2104.04538v1, Not Published.
[34]	Khetan, N., et al. (2021) Astronomy and Astrophysics, 647, Article No. A72. https://doi.org/10.1051/0004-6361/202039196
[35]	Mukherjee, S., et al. (2021) Astronomy and Astrophysics, 646, Article No. A65. https://doi.org/10.1051/0004-6361/201936724
[36]	Park, J.W., et al. (2021) The Astrophysical Journal, 910, Article No. 39. https://doi.org/10.3847/1538-4357/abdfc4
[37]	Philcox, O.H.E., Sherwin, B.D., Farren, G.S. and Baxter, E.J. (2021) Physical Review D, 103, Article ID: 023538. https://doi.org/10.1103/PhysRevD.103.023538
[38]	Qi, J.-Z., Zhao, J.-W., Cao, S., Biesiada, M. and Liu, Y. (2021) Monthly Notices of the Royal Astronomical Society, 503, 2179-2186. https://doi.org/10.1093/mnras/stab638
[39]	Riess, et al. (2021) The Astrophysical Journal Letters, 908, L6. https://doi.org/10.3847/2041-8213/abdbaf
[40]	Soltis, J., Casertano, S. and Riess, A.G. (2021) The Astrophysical Journal Letters, 908, L5. https://doi.org/10.3847/2041-8213/abdbad
[41]	Wang, H. and Giannios, D. (2021) The Astrophysical Journal, 908, Article No. 200. https://doi.org/10.3847/1538-4357/abd39c
[42]	Zhang, J.-C., Jiao, K. and Zhang, T.-J. (2021) Model-Independent meAsurement of the Hubble Constant and the Absolute Magnitude of Type Ia Supernovae. Not Published. arXiv:2101.05897.
[43]	Aghanim, N.A., Forveille, T., Pentericci, L. and Shore, S. (2020) Astronomy & Astrophysics, 641, Article No. E1. https://doi.org/10.1051/0004-6361/202039265
[44]	Benevento, G., Hu, W. and Raveri, M. (2020) Physical Review D, 101, Article ID: 103517. https://doi.org/10.1103/PhysRevD.101.103517
[45]	Birrer, S., et al. (2020) Astronomy & Astrophysics, 643, Article No. A165. https://doi.org/10.1051/0004-6361/202038861
[46]	Camarena, D. and Marra, V. (2020) Physical Review Research, 2, Article ID: 013028. https://doi.org/10.1103/PhysRevResearch.2.013028
[47]	Chang, Z. and Zhu, Q.-H. (2020) Physical Review D, 101, Article ID: 084029. https://doi.org/10.1103/PhysRevD.101.084029
[48]	Coughlin, M.W., et al. (2020) Nature Communications, 11, Article No. 4129. https://doi.org/10.1038/s41467-020-17998-5
[49]	D’Agostino, R. and Nunes, R.C. (2020) Physical Review D, 101, Article ID: 103505. https://doi.org/10.1103/PhysRevD.101.103505
[50]	Dai, W.M., Ma, Y.-Z. and He, H.-J. (2020) Physical Review D, 102, Article ID: 121302. https://doi.org/10.1103/PhysRevD.102.121302
[51]	Dietrich, T., et al. (2020) Science, 370, 1450-1453. https://doi.org/10.1126/science.abb4317
[52]	Gonzalez, M., Hertzberg, M.P. and Rompineve, F. (2020) Journal of Cosmology and Astroparticle Physics, 10, Article No. 028. https://doi.org/10.1088/1475-7516/2020/10/028
[53]	González-Serrena, B., Cuesta, A.J. and Ortiz-Mora, A. (2020) Contributions to the XIV.0 Scientific Meeting (Virtual) of the Spanish Astronomical Society.
[54]	Haboury, N. (2020) Measuring the Hubble Constant with Standard Sirens. University of Geneva, Astronomy Department, Geneva, 1-22, Not Published. https://www.researchgate.net/publication/343679057_Measuring_the_Hubble_constant_with_standard_sirens
[55]	Harvey, D. (2020) Monthly Notices of the Royal Astronomical Society, 498, 2871-2886. https://doi.org/10.1093/mnras/staa2522
[56]	Holanda, R.F.L., Pordeus-da-Silva, G. and Pereira, S.H. (2020) Journal of Cosmology and Astroparticle Physics, 9, Article No. 053. https://doi.org/10.1088/1475-7516/2020/09/053
[57]	Howlett, C. and Davis, T.M. (2020) Monthly Notices of the Royal Astronomical Society, 492, 3803-3815. https://doi.org/10.1093/mnras/staa049
[58]	De Jaeger, T., Stahl, B.E., Zheng, W., Filippenko, A.V., Riess, A.G. and Galbany, L. (2020) Monthly Notices of the Royal Astronomical Society, 496, 3402–3411. https://doi.org/10.1093/mnras/staa1801
[59]	Kim, Y.J., Kang, J., Lee, M.G. and Jang, I.S. (2020) The Astrophysical Journal, 905, Article No. 104. https://doi.org/10.3847/1538-4357/abbd97
[60]	Kreisch, C.D., Cyr-Racine, F.-Y. and Doré, O. (2020) Physical Review D, 101, Arrticle ID: 123505. https://doi.org/10.1103/PhysRevD.101.123505
[61]	Li, H. and Zhang, X. (2020) Science Bulletin, 65, 1419-1421. https://doi.org/10.1016/j.scib.2020.04.038
[62]	Lombriser, L. (2020) Physics Letters B, 803, Arrticle ID: 135303. https://doi.org/10.1016/j.physletb.2020.135303
[63]	Millon, M., et al. (2020) Astronomy and Astrophysics, 639, Article No. A101. https://doi.org/10.1051/0004-6361/201937351
[64]	Mukherjee, S., Ghosh, A., Graham, M.J., Karathanasis, C., et al. (2020) First Measurement of the Hubble Parameter from Bright Binary Black Hole GW190521. Not Published (Under Review with MNRAS), arXiv:2009.14199, 1 8.
[65]	Nicolaou, C., Lahav, O., Lemos, P., Hartley, W. and Braden, J. (2020) Monthly Notices of the Royal Astronomical Society, 495, 90-97. https://doi.org/10.1093/mnras/staa1120
[66]	Niedermann, F. and Sloth, M.S. (2020) Physical Review D, 102, Article ID: 063527. https://doi.org/10.1103/PhysRevD.102.063527
[67]	Palmese, A., et al. (2020) The Astrophysical Journal Letters, 900, Article No. L33. https://doi.org/10.3847/2041-8213/abaeff
[68]	Pandey, K.L., Karwalb, T. and Dasc, S. (2020) Journal of Cosmology and Astroparticle Physics, 7, Article No. 026. https://doi.org/10.1088/1475-7516/2020/01/026
[69]	Pesce, D.W., Braatz, J.A., Reid, M.J., Riess, A.G., et al. (2020) The Astrophysical Journal, 891, Article No. L1. https://doi.org/10.3847/2041-8213/ab75f0
[70]	Pogosian, L., Zhao, G.-B. and Jedamzik, K. (2020) The Astrophysical Journal Letters, 904, Article No. L17. https://doi.org/10.3847/2041-8213/abc6a8
[71]	Guo, R.-Y., Zhang, J.-F. and Zhang, X. (2020) Science China Physics, Mechanics & Astronomy, 63, Article No. 290406. https://doi.org/10.1007/s11433-019-1514-0
[72]	Schombert, J., McGaugh, S. and Lelli, F. (2020) The Astronomical Journal, 160, Article No. 71. https://doi.org/10.3847/1538-3881/ab9d88
[73]	Shajib, A.J., et al. (2020) Monthly Notices of the Royal Astronomical Society, 494, 6072-6102. https://doi.org/10.1093/mnras/staa828
[74]	Sharov, G.S. and Sinyakov, E.S. (2020) Mathematical Modelling and Geometry, 8, 1-20. https://doi.org/10.26456/mmg/2020-811
[75]	Vasylyev, S.S. and Filippenko, A.V. (2020) The Astrophysical Journal, 902, Article No. 149. https://doi.org/10.3847/1538-4357/abb5f9
[76]	Vogl, V. (2020) Cosmological Distances of Type II Supernovae from Radiative Transfer Modeling. Dissertation, Max-Planck-Institut Fur Astrophysik, Garching bei München, 172 p, Not Published. https://mediatum.ub.tum.de/doc/1542626/1542626.pdf
[77]	Wei, J.-J. and Melia, F. (2020) The Astrophysical Journal, 897, Article No. 127. https://doi.org/10.3847/1538-4357/ab959b
[78]	Wu, W.L.K., Motloch, P., Hu, W. and Raveri, M. (2020) Physical Review D, 102, Article ID: 023510. https://doi.org/10.1103/PhysRevD.102.023510
[79]	Yang, T., Birrer, S. and Hu, B. (2020) Monthly Notices of the Royal Astronomical Society, 497, L56-L61. https://doi.org/10.1093/mnrasl/slaa107
[80]	Zhang, X. and Huang, Q.-G. (2020) Science China Physics Mechanical Astronomy, 63, Article No. 290402. https://doi.org/10.1007/s11433-019-1504-8
[81]	Agrawal, P., Cyr-Racine, F.-Y., Pinner, D. and Randall, L. (2019) Rock ‘n’ Roll Solutions to the Hubble Tension. Cornell University, Ithaca, arXiv:1904.01016v1, Not Published.
[82]	Anderson, R.I. (2019) Astronomy & Astrophysics, 631, Article No. A165. https://doi.org/10.1051/0004-6361/201936585
[83]	Birrer, S., Treu, T., Rusu, C.E., Bonvin, V., et al. (2019) Monthly Notices of the Royal Astronomical Society, 484, 4726-4753. https://doi.org/10.1093/mnras/stz200
[84]	Chang, Z., Huang, Q.-G., Wang, S. and Zhao, Z.-C. (2019) The European Physical Journal C, 79, Article No. 177. https://doi.org/10.1140/epjc/s10052-019-6664-0
[85]	Chen, G.C.-F., Fassnacht, C.D., Suyu, S.H., Rusu CE, et al. (2019) Monthly Notices of the Royal Astronomical Society, 490, 1743-1773. https://doi.org/10.1093/mnras/stz2547
[86]	Collett, T., Montanari, F. and Räsänen, S. (2019) Physical Review Letters, 123, Article ID: 231101. https://doi.org/10.1103/PhysRevLett.123.231101
[87]	Cuceu, A., Farr, J., Lemos, P. and Font-Ribera, A. (2019) Journal of Cosmology and Astroparticle Physics, 10, Article No. 044. https://doi.org/10.1088/1475-7516/2019/10/044
[88]	Domínguez, A., et al. (2019) The Astrophysical Journal, 885, Article No. 137. https://doi.org/10.3847/1538-4357/ab4a0e
[89]	Dutta, K., et al. (2019) Physical Review D, 100, Article ID: 075028. https://doi.org/10.1103/PhysRevD.100.075028
[90]	Fishbach, M., et al. (2019) The Astrophysical Journal Letters, 871, Article No. L13. https://doi.org/10.3847/2041-8213/aaf96e
[91]	Freedman, W.L., et al. (2019) The Astrophysical Journal, 882, Article No. 34. https://doi.org/10.3847/1538-4357/ab2f73
[92]	Guo, R.-Y., Zhang, J.-F. and Zhang, X. (2019) Journal of Cosmology and Astroparticle Physics, 2, Article No. 054. https://doi.org/10.1088/1475-7516/2019/02/054
[93]	Hotokezaka, K., et al. (2019) Nature Astronomy, 3, 940-944. https://doi.org/10.1038/s41550-019-0820-1
[94]	Jee, I., et al. (2019) Science, 365, 1134-1138. https://doi.org/10.1126/science.aat7371
[95]	Kozmanyan, A., Bourdin, H., Mazzotta, P., Rasia, E. and Sereno, M. (2019) Astronomy & Astrophysics, 621, Article No. A34. https://doi.org/10.1051/0004-6361/201833879
[96]	Liao, K., Shafieloo, A., Keeley, R.E. and Linder, E.V. (2019) The Astrophysical Journal Letters, 886, Article No. L23. https://doi.org/10.3847/2041-8213/ab5308
[97]	Macaulay, E., et al. (2019) Monthly Notices of the Royal Astronomical Society, 486, 2184-2196. https://doi.org/10.1093/mnras/stz978
[98]	Martinelli, M. and Tutusaus, I. (2019) Symmetry, 11, Article No. 986. https://doi.org/10.3390/sym11080986
[99]	Park, C.-G. and Ratra, B. (2019) Astrophysics and Space Science, 364, Article No. 134. https://doi.org/10.1007/s10509-019-3627-8
[100]	Reid, M.J., Pesce, D.W. and Riess, A.G. (2019) The Astrophysical Journal, 886, Article No. L27. https://doi.org/10.3847/2041-8213/ab552d
[101]	Riess, A.G., et al. (2019) The Astrophysical Journal, 876, Article No. 85. https://doi.org/10.3847/1538-4357/ab1422
[102]	Riess, A.G. (2019) Nature Reviews Physics, 2, 10-12. https://doi.org/10.1038/s42254-019-0137-0
[103]	Rusu, C.E., et al. (2020) Monthly Notices of the Royal Astronomical Society, 498, 1440-1468. https://doi.org/10.1093/mnras/stz3451
[104]	Ryan, J., Chen, Y. and Ratra, B. (2019) Monthly Notices of the Royal Astronomical Society, 488, 3844-3856. https://doi.org/10.1093/mnras/stz1966
[105]	Saha, S. and Sahoo, S. (2019) The African Review of Physics, 14, 7-9.
[106]	Shajib, A.J., Birrer, S., Treu, T., Agnello, A., et al. (2019) Monthly Notices of the Royal Astronomical Society, 494, 6072-6102. https://doi.org/10.1093/mnras/staa828
[107]	Soares-Santos, M., et al. (2019) The Astrophysical Journal Letters, 876, Article No. L7. https://doi.org/10.3847/2041-8213/ab14f1
[108]	Taubenberger, S., et al. (2019) Astronomy and Astrophysics, 628, Article No. L7. https://doi.org/10.1051/0004-6361/201935980
[109]	Tiwari, S., Haney, M. and Boetzel, Y. (2019) A Gravitational-Wave Measurement of the Hubble Constant Following the Second Observing Run of Advanced LIGO and Virgo. University of Zurich, Zurich, Not Published. arXiv.org 1908.06060.
[110]	Verde, L., Treu, T. and Riess, A.G. (2019) Nature Astronomy, 3, 891-895. https://doi.org/10.1038/s41550-019-0902-0
[111]	Wong, K.C., et al. (2019) Monthly Notices of the Royal Astronomical Society, 498, 1420-1439. https://doi.org/10.1093/mnras/stz3094
[112]	Yuan, W., et al. (2019) The Astrophysical Journal, 886, Article No. 61. https://doi.org/10.3847/1538-4357/ab4bc9
[113]	Zhang, X. and Huang, Q.-G. (2019) Communications in Theoretical Physics, 71, 826-830. https://doi.org/10.1088/0253-6102/71/7/826
[114]	Zeng, H. and Yan, D. (2019) The Astrophysical Journal, 882, Article No. 87. https://doi.org/10.3847/1538-4357/ab35e3
[115]	Abbott, T.M.C., et al. (2018) Monthly Notices of the Royal Astronomical Society, 480, 3879-3888. https://doi.org/10.1093/mnras/sty1939
[116]	Benetti, M., Graef, L.L. and Alcaniz, J.S. (2018) Journal of Cosmology and Astroparticle Physics, 7, Article No. 066. https://doi.org/10.1088/1475-7516/2018/07/066
[117]	Bolejko, K. (2018) Physical Review D, 97, Article ID: 083515. https://doi.org/10.1103/PhysRevD.97.083515
[118]	Braatz, J., et al. (2018) Proceedings of the International Astronomical Union, 13, 86-91. https://doi.org/10.1017/S1743921317010249
[119]	Cantiello, M., et al. (2018) The Astrophysical Journal Letters, 854, Article No. L31. https://doi.org/10.3847/2041-8213/aaad64
[120]	Chen, H.-Y., Fishbach, M. and Holz, D.E. (2018) Nature, 562, 545-547. https://doi.org/10.1038/s41586-018-0606-0
[121]	Choudhury, S.R. and Choubey, S. (2019) Journal of Cosmology and Astroparticle Physics, 9, Article No. 017. https://doi.org/10.1088/1475-7516/2018/09/017
[122]	Dhawan, S., Jha, S.W. and Leibundgut, B. (2018) Astronomy and Astrophysics, 609, Article No. A72. https://doi.org/10.1051/0004-6361/201731501
[123]	Di Valentino, E. and Melchiorri, A. (2018) Physical Review D, 97, Article ID: 041301. https://doi.org/10.1103/PhysRevD.97.041301
[124]	Gómez-Valent, A. and Amendola, L. (2018) Journal of Cosmology and Astroparticle Physics, 4, Article No. 051. https://doi.org/10.1088/1475-7516/2018/04/051
[125]	Grillo, C., et al. (2018) The Astrophysical Journal, 860, Article No. 94. https://doi.org/10.3847/1538-4357/aac2c9
[126]	Hoeneisen, B. (2018) International Journal of Astronomy and Astrophysics, 8, 386-405. https://doi.org/10.4236/ijaa.2018.84027
[127]	Lee, M.G. and Jang, I.S. (2018) The TRGB and the Hubble Constant in 2017: TIPSNU. In: Jensen, J., Michael Rich, R. and de Grijs, R., Eds., Stellar Populations and the Distance Scale, Vol. 514, Astronomical Society of the Pacific, San Francisco, 143-150.
[128]	Riess, A.G., et al. (2018) The Astrophysical Journal, 861, 1-13.
[129]	Riess, A.G., et al. (2018) The Astrophysical Journal, 855, Article No. 136.
[130]	Van Putten, M.H.P.M. (2018) European Physical Journal Web of Conferences, 168, Article No. 08005. https://doi.org/10.1051/epjconf/201816808005
[131]	Vitale, S. and Chen, H.-Y. (2018) Physical Review Letters, 121, Article ID: 021303. https://doi.org/10.1103/PhysRevLett.121.021303
[132]	Yu, H., Ratra, B. and Wang, F.-Y. (2018) The Astrophysical Journal, 856, Article No. 3. https://doi.org/10.3847/1538-4357/aab0a2
[133]	Zhang, J. (2018) Publications of the Astronomical Society of the Pacific, 130, Article ID: 117002. https://doi.org/10.1088/1538-3873/aae4ca
[134]	Abbott, B.P., et al. (2017) Nature, 551, 85-88. https://doi.org/10.1038/nature24471
[135]	Bethapudi, S. and Desai, S. (2017) The European Physical Journal Plus, 132, Article No. 78. https://doi.org/10.1140/epjp/i2017-11390-3
[136]	Bonvin, V., et al. (2017) Monthly Notices of the Royal Astronomical Society, 465, 4914-4930. https://doi.org/10.1093/mnras/stw3006
[137]	Cardona, W., Kunza, M. and Valeria, P. (2017) Journal of Cosmology and Astroparticle Physics, 3, Article No. 056. https://doi.org/10.1088/1475-7516/2017/03/056
[138]	Chen, Y., Kumar, S. and Ratra, B. (2017) The Astrophysical Journal, 835, Article No. 86. https://doi.org/10.3847/1538-4357/835/1/86
[139]	Farooq, O., Madiyar, F.R., Crandall, S. and Ratra, B. (2017) The Astrophysical Journal, 835, Article No. 26. https://doi.org/10.3847/1538-4357/835/1/26
[140]	Feeney, S.M., Mortlock, D.J. and Dalmasso, N. (2017) Monthly Notices of the Royal Astronomical Society, 476, 3861-3882. https://doi.org/10.1093/mnras/sty418
[141]	Grieb, J.N., et al. (2017) Monthly Notices of the Royal Astronomical Society, 467, 2085-2112. https://doi.org/10.1093/mnras/stw3384
[142]	Guo, R.-Y. and Zhang, X. (2017) The European Physical Journal C, 77, Article No. 882. https://doi.org/10.1140/epjc/s10052-017-5454-9
[143]	Hjorth, J., et al. (2017) The Astrophysical Journal Letters, 848, Article No. L31. https://doi.org/10.3847/2041-8213/aa9110
[144]	Huang, H. and Huang, L. (2017) International Journal of Modern Physics D, 26, Article No. 1740001. https://doi.org/10.1142/S0218271817400016
[145]	Jang, I.S. and Lee, M.G. (2017) The Astrophysical Journal, 836, Article No. 74. https://doi.org/10.3847/1538-4357/836/1/74
[146]	Pritychenko, B. (2017) EPJ Web of Conferences, 146, Article No. 01006. https://doi.org/10.1051/epjconf/201714601006
[147]	Wang, Y., Xu, L. and Zhao, G.-B. (2017) The Astrophysical Journal, 849, Article No. 84. https://doi.org/10.3847/1538-4357/aa8f48
[148]	Wei, J.-J. and Wu, X.-F. (2017) The Astrophysical Journal, 838, Article No. 160. https://doi.org/10.3847/1538-4357/aa674b
[149]	Wong, K.C., et al. (2017) Monthly Notices of the Royal Astronomical Society, 465, 4895-4913. https://doi.org/10.1093/mnras/stw3077
[150]	Zhang, B.R. (2017) Monthly Notices of the Royal Astronomical Society, 471, 2254-2285. https://doi.org/10.1093/mnras/stx1600
[151]	Ade, P.A.R., et al. (2016) Astronomy & Astrophysics, 594, Article No. A13. https://doi.org/10.1051/0004-6361/201525830
[152]	Gao, F., et al. (2016) The Astrophysical Journal, 817, Article No. 128. https://doi.org/10.3847/0004-637X/817/2/128
[153]	Ichiki, K., Yoo, C.-M. and Oguri, M. (2016) Physical Review D, 93, Article ID: 023529. https://doi.org/10.1103/PhysRevD.93.023529
[154]	Ludović, V.V., D’Agostino, R. and Vittorio, N. (2016) Astronomy and Astrophysics, 595, Article No. A109. https://doi.org/10.1051/0004-6361/201628217
[155]	Moresco, M., et al. (2016) Journal of Cosmology and Astroparticle Physics, 5, Article No. 014. https://doi.org/10.1088/1475-7516/2016/05/014
[156]	Riess, A.G., et al. (2016) The Astrophysical Journal, 826, Article No. 56. https://doi.org/10.3847/0004-637X/826/1/56
[157]	Tully, R.B., Courtois, H.M. and Sorce, J.G. (2016) The Astronomical Journal, 152, Article No. 50. https://doi.org/10.3847/0004-6256/152/2/50
[158]	Cheng, C. and Huang, Q.G. (2015) Science China Physics, Mechanics & Astronomy, 58, Article No. 599801. https://doi.org/10.1007/s11433-015-5684-5
[159]	Cuesta, A.J., Verde, L., Riess, A. and Jimenez, R. (2015) Monthly Notices of the Royal Astronomical Society, 448, 3463-3471. https://doi.org/10.1093/mnras/stv261
[160]	Jang, I.S. and Lee, M.G. (2015) The Astrophysical Journal, 807, Article No. 133. https://doi.org/10.1088/0004-637X/807/2/133
[161]	Kumar, S.R., Stalin, C.S. and Prabhu, T.P. (2015) Astronomy and Astrophysics, 580, Article No. A38. https://doi.org/10.1051/0004-6361/201423977
[162]	Kuo, C.Y., Braatz, J.A., Lo, K.Y., Reid, M.J., Suyu, S.H., Pesce, D.W., Condon, J.J., Henkel, C. and Impellizzeri, C.M.V. (2015) The Astrophysical Journal, 800, Article No. 26. https://doi.org/10.1088/0004-637X/800/1/26
[163]	Rigault, M. and Schombert, J.M. (2015) The Astrophysical Journal, 802, Article No. 18. https://doi.org/10.1088/0004-637X/802/1/18
[164]	Ade, P.A.R., et al. (2014) Astronomy & Astrophysics, 571, Article No. A16. https://doi.org/10.1051/0004-6361/201321591
[165]	Ben-Dayan, I., Durrer, R., Marozzi, G. and Schwarz, D.J. (2014) Physical Review Letters, 112, Article ID: 221301. https://doi.org/10.1103/PhysRevLett.112.221301
[166]	Bennett, C.L., et al. (2014) The Astrophysical Journal, 794, Article No. 135. https://doi.org/10.1088/0004-637X/794/2/135
[167]	Busti, V.C., Clarkson, C. and Seikel, M. (2014) Proceedings of the International Astronomical Union, 10, 25-27. https://doi.org/10.1017/S1743921314013751
[168]	Efstathiou, G. (2014) Monthly Notices of the Royal Astronomical Society, 440, 1138-1152. https://doi.org/10.1093/mnras/stu278
[169]	Lima, J.A.S. and Cunha, J.V. (2014) The Astrophysical Journal Letters, 781, Article No. L38. https://doi.org/10.1088/2041-8205/781/2/L38
[170]	Bennett, C.L., et al. (2013) The Astrophysical Journal, 208, Article No. 20. https://doi.org/10.1088/0067-0049/208/2/20
[171]	Braatz, J., et al. (2013) Proceedings of the International Astronomical Union, 8, 255-261. https://doi.org/10.1017/S1743921312021515
[172]	Farooq, O. and Rathra, B. (2013) The Astrophysical Journal Letters, 766, Article No. L7. https://doi.org/10.1088/2041-8205/766/1/L7
[173]	Hinshaw, G., et al. (2013) The Astrophysical Journal Supplement Series, 208, Article No. 19. https://doi.org/10.1088/0067-0049/208/2/19
[174]	Humphreys, E.M.L., Reid, M.J., Moran, J.M., Greenhill, L.J. and Argon, A.L. (2013) The Astrophysical Journal, 775, Article No. 13. https://doi.org/10.1088/0004-637X/775/1/13
[175]	Kuo, C.Y., Braatz, J.A., Reid, M.J., Lo, K.Y., Condon, J.J., Impellizzeri, C.M.V. and Henkel, C. (2013) The Astrophysical Journal, 767, Article No. 155. https://doi.org/10.1088/0004-637X/767/2/155
[176]	Pietrzyński, G., et al. (2013) Nature, 495, 76-79. https://doi.org/10.1038/nature11878
[177]	Reid, M.J., et al. (2013) The Astrophysical Journal, 767, Article No. 154. https://doi.org/10.1088/0004-637X/767/2/154
[178]	Salvatelli, V., Marchini, A., Lopez-Honorez, L. and Mena, O. (2013) Physical Review D, 88, Article ID: 023531. https://doi.org/10.1103/PhysRevD.88.023531
[179]	Scowcroft, V., et al. (2013) Proceedings of the International Astronomical Union, 8, 274-281. https://doi.org/10.1017/S1743921312021540
[180]	Sereno, M. and Paraficz, D. (2013) Monthly Notices of the Royal Astronomical Society, 437, 600-605. https://doi.org/10.1093/mnras/stt1938
[181]	Suyu, S.H., et al. (2013) The Astrophysical Journal, 766, Article No. 70. https://doi.org/10.1088/0004-637X/766/2/70
[182]	Tully, R.B., et al. (2013) The Astronomical Journal, 146, Article No. 86. https://doi.org/10.1088/0004-6256/146/4/86
[183]	Xia, J.-Q., Li, H. and Zhang, X. (2013) Physical Review D, 88, Article ID: 063501. https://doi.org/10.1103/PhysRevD.88.063501
[184]	Calabrese, E., Archidiacono, M., Melchiorri, A. and Ratra, B. (2012) Physical Review D, 86, Article ID: 043520. https://doi.org/10.1103/PhysRevD.86.043520
[185]	Chávez, R., et al. (2012) Monthly Notices of the Royal Astronomical Society, 425, L56-L60. https://doi.org/10.1111/j.1745-3933.2012.01299.x
[186]	Colless, M., Beutler, F. and Blake, C. (2012) Proceedings of the International Astronomical Union, 8, 319-322. https://doi.org/10.1017/S1743921312021618
[187]	Freedman, W.L., et al. (2012) The Astrophysical Journal, 758, Article No. 24. https://doi.org/10.1088/0004-637X/758/1/24
[188]	Del Pozzo, W. (2012) Physical Review D, 86, Article ID: 043011. https://doi.org/10.1103/PhysRevD.86.043011
[189]	Riess, A.G., Fliri, J. and Valls-Gabaud, D. (2012) The Astrophysical Journal, 745, Article No. 156. https://doi.org/10.1088/0004-637X/745/2/156
[190]	Wang, M. (2012) AIP Conference Proceedings, 1441, 503-505. https://doi.org/10.1063/1.3700599
[191]	Chen, G. and Ratra, B. (2011) Publications of the Astronomical Society of the Pacific, 123, Article No. 1127. https://doi.org/10.1086/662131
[192]	Beutler, F., et al. (2011) Monthly Notices of the Royal Astronomical Society, 416, 3017-3032. https://doi.org/10.1111/j.1365-2966.2011.19250.x
[193]	Jarosik, N., et al. (2011) The Astrophysical Journal Supplement Series, 192, Article No. 14. https://doi.org/10.1088/0067-0049/192/2/14
[194]	Riess, A.G., et al. (2011) The Astrophysical Journal, 730, Article No. 119. https://doi.org/10.1088/0004-637X/730/2/119
[195]	Freedman, W.L. and Madore, B.F. (2010) Annual Review of Astronomy and Astrophysics, 48, 673-710. https://doi.org/10.1146/annurev-astro-082708-101829
[196]	Paraficz, D. and Hjorth, J. (2010) The Astrophysical Journal, 712, 1378-1384. https://doi.org/10.1088/0004-637X/712/2/1378
[197]	Suyu, S.H., et al. (2010) The Astrophysical Journal, 711, 201-221. https://doi.org/10.1088/0004-637X/711/1/201
[198]	Hinshaw, G., et al. (2009) The Astrophysical Journal Supplement Series, 180, 225-245. https://doi.org/10.1088/0067-0049/180/2/225
[199]	Komatsu, et al. (2009) The Astrophysical Journal Supplement Series, 180, 330-376. https://doi.org/10.1088/0067-0049/180/2/330
[200]	Riess, A.G., et al. (2009) The Astrophysical Journal, 699, 539-563. https://doi.org/10.1088/0004-637X/699/1/539
[201]	Russell, D.G. (2009) Journal of Astrophysics and Astronomy, 30, 93-118. https://doi.org/10.1007/s12036-009-0006-9
[202]	Leith, B.M., Ng, S.C.C. and Wiltshir, D.L. (2008) The Astrophysical Journal, 672, L91-L94. https://doi.org/10.1086/527034
[203]	Vuissoz, C., et al. (2008) Astronomy & Astrophysics, 488, 481-490. https://doi.org/10.1051/0004-6361:200809866
[204]	Oguri, M. (2007) The Astrophysical Journal, 660, 1-15. https://doi.org/10.1086/513093
[205]	Spergel, D.N., et al. (2007) The Astrophysical Journal Supplement Series, 170, 377-408. https://doi.org/10.1086/513700
[206]	Bonamente, M., Joy, M.K., La Roque, S.J. and Carlstrom, J.E. (2006) The Astrophysical Journal, 647, 25-54. https://doi.org/10.1086/505291
[207]	Hütsi, G. (2006) Cosmic Sound: Measuring the Universe with Baryonic Acoustic Oscillations. Dissertation, Ludwig Maximilian University of Munich, München, 1-148, Not Published. (uni-muenchen.de)
[208]	Ngeow, C. and Kanbur, S.M. (2006) The Astrophysical Journal, 642, L29-L32. https://doi.org/10.1086/504478
[209]	Sandage, A., et al. (2006) The Astrophysical Journal, 653, 843-860. https://doi.org/10.1086/508853
[210]	Wang, X., Wang, L., Pain, R., Zhou, X. and Li, Z. (2006) The Astrophysical Journal, 645, 488-505. https://doi.org/10.1086/504312
[211]	Gibson, B.K. and Brook, C.B. (2005) Symposium—International Astronomical Union, 201, 200-208. https://doi.org/10.1017/S0074180900216264
[212]	Hamuy, M. (2005) The Standard Candle Method for Type II Supernovae and the Hubble Constan. In: Marcaide, J.M and Weiler, K.W., Eds., Cosmic Explosions, Vol. 99, Springer, Berlin, Heidelberg, 535-541. https://doi.org/10.1007/3-540-26633-X_71
[213]	Magain, P. (2005) Time Delay in Gravitational Lenses: An Alternative Route to the Hubble Constant. Proceedings of ASP Conference Series, Vol. 335, Brussels, 19-22 July 2004, 207-214.
[214]	Olivares, G., Atrio-Barandela, F. and Pavón, D. (2005) Physical Review D, 71, Article ID: 063523. https://doi.org/10.1103/PhysRevD.71.063523
[215]	Riess, A.G. (2005) The Astrophysical Journal, 627, 579-607. https://doi.org/10.1086/430497
[216]	Schmidt, R.W., Allen, S.W. and Fabian, A.C. (2004) Monthly Notices of the Royal Astronomical Society, 352, 1413-1420. https://doi.org/10.1111/j.1365-2966.2004.08032.x
[217]	Stritzinger, M. and Leibundgut, B. (2004) Astronomy & Astrophysics, 431, 423-431. https://doi.org/10.1051/0004-6361:20041630
[218]	Udomprasert, P.S., Mason, B.S., Readhead, A.C.S. and Pearson, T.J. (2004) The Astrophysical Journal, 615, 63-81. https://doi.org/10.1086/423946
[219]	Boffi, F.R. and Riess, A.G. (2003) The Type Ia Supernova 1998aq and the Hubble Constant. ASP Conference Proceedings, Vol. 303, La Palma, 27-31 May 2002, 101-104.
[220]	Dumin, Y.V. (2003) Advances in Space Research, 31, 2461-2466. https://doi.org/10.1016/S0273-1177(03)00533-7
[221]	Jimenez, R., Verde, L., Treu, T. and Stern, D. (2003) The Astrophysical Journal, 593, 622-629. https://doi.org/10.1086/376595
[222]	Koopmans, L.V.E., Treu, T., Fassnacht, C.D., Blandford, R.D. and Surpi, G. (2003) The Astrophysical Journal, 599, 70-85. https://doi.org/10.1086/379226
[223]	Mei, S., Scodeggio, M., Silva, D.R. and Quinn, P.J. (2003) Astronomy and Astrophysics, 399, 441-448. https://doi.org/10.1051/0004-6361:20021800
[224]	Saunders, R., et al. (2003) Monthly Notices of the Royal Astronomical Society, 341, 937-940. https://doi.org/10.1046/j.1365-8711.2003.06467.x
[225]	Spergel, D.N., et al. (2003) The Astrophysical Journal Supplement Series, 148, 175-174. https://doi.org/10.1086/377226
[226]	Fassnacht, C.D., Xanthopoulos, E., Koopmans, L.V.E. and Rusin, D. (2002) The Astrophysical Journal, 581, 823-835. https://doi.org/10.1086/344368
[227]	Freedman, W.L. (2002) The Status of the Hubble Constant. In: Metcalfe, N. and Shanks, T., Eds., A New Era in Cosmology. ASP Conference Proceedings, Vol. 283, Astronomical Society of the Pacific, San Francisco, 249-257.
[228]	Grainge, K., et al. (2002) Monthly Notices of the Royal Astronomical Society, 333, 318-326. https://doi.org/10.1046/j.1365-8711.2002.05429.x
[229]	Kochanek, C.S. (2002) Gravitational Lenses, the Distance Ladder and the Hubble Constant: A New Dark Matter Problem. arXiv:astro-ph/0204043v1.
[230]	Tikhonov, N.A. and Galazoutdinova, O.A. (2002) Astrophysics, 45, 253-266. https://doi.org/10.1023/A:1020168130980
[231]	Treu, T. and Koopmans, L.V.E. (2002) Monthly Notices of the Royal Astronomical Society, 337, L6-L10. https://doi.org/10.1046/j.1365-8711.2002.06107.x
[232]	Freedman, W.L., et al. (2001) The Astrophysical Journal, 553, 47-72. https://doi.org/10.1086/320638
[233]	Itoh, N. (2001) The Astronomical Herald, 94, 214-220.
[234]	Jensen, J.B., et al. (2001) The Astrophysical Journal, 550, 503-521. https://doi.org/10.1086/319819
[235]	Koopmans, L.V.E. and The CLASS Collaboration (2001) Publication of Astronomical Society of Australia, 18, 179-181. https://doi.org/10.1071/AS01024
[236]	Liu, M.C. and Graham, J.R. (2001) The Astrophysical Journal, 557, L31-L34. https://doi.org/10.1086/323174
[237]	Mason, B.S., Myers, S.T. and Readhead, A.C.S. (2001) The Astrophysical Journal, 555, L11-L15. https://doi.org/10.1086/321737
[238]	Mei, S., Quinn, P.J. and Silva, D.R. (2001) Astronomy and Astrophysics, 371, 779-794. https://doi.org/10.1051/0004-6361:20010427
[239]	Tonry, J.L. and High-Z Supernova Search Team (2001) Type Ia Supernovae, the Hubble Constant, the Cosmological Constant and the Age of the Universe. In: von Hippel, T., Simpson, C. and Manset, N., Eds., Astrophysical Ages and Times Scales, ASP Conference Series, Vol. 245, San Francisc, Astronomical Society of the Pacific, 593-601.
[240]	Willick, J.A. and Batra, P. (2001) The Astrophysical Journal, 548, 564-584. https://doi.org/10.1086/319005
[241]	Wang, X.-F., Chen, L. and Li, Z.-W. (2001) Chinese Physics Letters, 18, 154-156. https://doi.org/10.1088/0256-307X/18/1/354
[242]	Ferrarese, L., et al. (2000) The Astrophysical Journal, 529, 745-767. https://doi.org/10.1086/308309
[243]	Gibson, B.K., et al. (2000) The Astrophysical Journal, 529, 723-744. https://doi.org/10.1086/308306
[244]	Mould, J.R., et al. (2000) The Astrophysical Journal, 529, 786-794. https://doi.org/10.1086/308304
[245]	Sakai, S. (2000) The Astrophysical Journal, 529, 698-722. https://doi.org/10.1086/308305
[246]	Tikhonov, N.A., Galazoutdinova, O.A. and Drozdovskii, I.O. (2000) Astrophysics, 43, 367-380. https://doi.org/10.1023/A:1010902305550
[247]	Biggs, A.D., Browne, I.W.A., Helbig, P., Koopmans, L.V.E., Wilkinson, P.N. and Perley, R.A. (1999) Monthly Notices of the Royal Astronomical Society, 304, 349-358. https://doi.org/10.1046/j.1365-8711.1999.02309.x
[248]	Chae, K.-H. (1999) The Astrophysical Journal, 524, 582-590. https://doi.org/10.1086/307842
[249]	Collier, S., Horne, K., Wanders, I. and Peterson, B.M. (1999) Monthly Notices of the Royal Astronomical Society, 302, L24-L28. https://doi.org/10.1046/j.1365-8711.1999.02250.x
[250]	Freedman, W.L. and Feng, L.L. (1999) Proceedings of the National Academy of Sciences of the United States of America, 96, 11063-11064. https://doi.org/10.1073/pnas.96.20.11063
[251]	Jha, S., et al. (1999) The Astrophysical Journal Supplement Series, 125, 73-97. https://doi.org/10.1086/313275
[252]	Mason, B.S. (1999) An Improved Measurement of the Hubble Constant Using the Sunyaev-Zeldovich Effect. Dissertations, University of Pennsylvania, Philadelphia, UMI Number: AAI9953569. https://repository.upenn.edu/dissertations/AAI9953569
[253]	Mazumdar, A. and Narasimba, D. (1999) Bulletin of the Astronomical Society of India, 27, 267.
[254]	Tanvir, N.R. (1999) Monthly Notices of the Royal Astronomical Society, 310, 175-188. https://doi.org/10.1046/j.1365-8711.1999.02954.x
[255]	Tripp, R. and Branch, D. (1999) The Astrophysical Journal, 525, 209-214. https://doi.org/10.1086/307883
[256]	Branch, D. (1998) Annual Review of Astronomy and Astrophysics, 36, 17-55. https://doi.org/10.1146/annurev.astro.36.1.17
[257]	Goicoechea, L.J., Mediavilla, E., Oscoz, A., Serra, M. and Buttrago, J. (1998) Astrophysics and Space Science, 261, 341-344. https://doi.org/10.1023/A:1002042026159
[258]	Harris, W.E., et al. (1998) Nature, 395, 45-47. https://doi.org/10.1038/25673
[259]	Hughes, J.P. and Birkinshaw, M. (1998) The Astrophysical Journal, 501, 1-14. https://doi.org/10.1086/305788
[260]	Lauer, T.R., Tonry, J.L., Postman, M., Ajhar, E.A. and Holtzman, J.A. (1998) The Astrophysical Journal, 499, 577-588. https://doi.org/10.1086/305671
[261]	Riess, A.G., et al. (1998) The Astronomical Journal, 116, 1009-1038. https://doi.org/10.1086/300499
[262]	Tamman, G.A. and Labhardt, L. (1998) A Forty-Year Search for the Hubble Constant. In: Riffert, H., Ruder, H., Nollert, H.P. and Hehl, F.W., Eds., Relativistic Astrophysics, Vieweg+Teubner Verlag, Wiesbaden, 238-261. https://doi.org/10.1007/978-3-663-11294-5_15
[263]	Tripp, R. (1998) Astronomy and Astrophysics, 331, 815-820.
[264]	Giovanelli, R. (1997) The Extragalactic Distance Scale. Proceedings of the ST ScI May Symposium, Baltimore, 7-10 May 1996, 113.
[265]	Gregg, M.D. (1997) New Astronomy, 1, 363-371. https://doi.org/10.1016/S1384-1076(97)00005-5
[266]	Hjorth, J. and Tanvir, N.R. (1997) The Astrophysical Journal, 482, 68-74. https://doi.org/10.1086/304124
[267]	Holzapfel, W.L., et al. (1997) The Astrophysical Journal, 480, 449-465. https://doi.org/10.1086/303979
[268]	Hoyle, F., Burhidge, G. and Narlikar, J.V. (1997) Monthly Notices of the Royal Astronomical Society, 286, 173-182. https://doi.org/10.1093/mnras/286.1.173
[269]	Schechter, P.L. (1997) The Astrophysical Journal, 475, L85-L88. https://doi.org/10.1086/310478
[270]	Sciama, D.W. (1997) Monthly Notices of the Royal Astronomical Society, 289, 945-947. https://doi.org/10.1093/mnras/289.4.945
[271]	Tonry, J.L., Blakeslee, J.P., Ajhar, E.A. and Dressler, A. (1997) The Astrophysical Journal, 475, 399-413. https://doi.org/10.1086/303576
[272]	Amendola, L. (1996) Astronomy and Astrophysics, 312, 353-356.
[273]	Biesiada, M. (1996) Monthly Notices of the Royal Astronomical Society, 283, 997-982. https://doi.org/10.1093/mnras/283.3.977
[274]	Forbes, D.A., Brodie, J.P. and Huchra, J. (1996) Astronomical Journal, 112, 2448-2460. https://doi.org/10.1086/118194
[275]	Kobyashi, S., Sasaki, S. and Suto, Y. (1996) Publications of the Astronomical Society of Japan, 48, L107-L111. https://doi.org/10.1093/pasj/48.6.L107
[276]	Mallik, D.C.V. (1996) Current Science, 71, 547-552. https://www.jstor.org/stable/24098091
[277]	Schaefer, B.E. (1996) The Astrophysical Journal, 460, L19-L23. https://doi.org/10.1086/309963
[278]	Grogin, N.A. and Narayan, R. (1995) The Astrophysical Journal, 473, 570-571. https://doi.org/10.1086/178171
[279]	Herbig, T., Lawrence, C.R., Readhead, A.C.S. and Gulkis, S. (1995) The Astrophysical Journal, 449, L5-L8. https://doi.org/10.1086/309616
[280]	Holzapfel, W.L., et al. (1995) Bulletin of the American Astronomical Society, 27, 1413.
[281]	Jones, M. (1995) Astrophysical Letters and Communications, 32, 347-353.
[282]	Kennicutt Jr., R.C., Freedman, W.L. and Mould, J.R. (1995) The Astrophysical Journal, 110, 1476-1491. https://doi.org/10.1086/117621
[283]	Mould, J., et al. (1995) The Astrophysical Journal, 449, 413-421.
[284]	Nakamura, T.T. and Suto, Y. (1995) Astrophysical Journal Letters, 447, L65-L68. https://doi.org/10.1086/309580
[285]	Raphaeli, Y. (1995) Annual Review of Astronomy and Astrophysics, 33, 541-579. https://doi.org/10.1146/annurev.aa.33.090195.002545
[286]	Scheafer, B.E. (1995) The Astrophysical Journal, 447, L13-L16.
[287]	Tanvir, N.R., Shanks, T., Ferguson, H.C. and Robinson, D.R.T. (1995) Nature, 377, 27-31. https://doi.org/10.1038/377027a0
[288]	Whitmore, B.C. and Schweizer, F. (1995) The Astronomical Journal, 210, 960-980 and 1411-1416 (For Graphics).
[289]	Birkinshaw, M. and Hughes, J.P. (1994) The Astrophysical Journal, 420, 33-43. https://doi.org/10.1086/173540
[290]	Freedman, W., et al. (1994) Nature, 371, 757-762. https://doi.org/10.1038/371757a0
[291]	Lu, N.Y., Salpeter, E.E. and Hoffman, G.L. (1994) The Astrophysical Journal, 426, 473-485. https://doi.org/10.1086/174083
[292]	Schmidt, B.P., et al. (1994) Astrophysical Journal, 432, 42-48.
[293]	Tully, R.B. (1993) Proceedings of the National Academy of Sciences of the United States of America, 90, 4806-4810. https://doi.org/10.1073/pnas.90.11.4806
[294]	Duemmler, R. (1992) Astronomy and Astrophysics, 264, 1-10.
[295]	Lauer, T.D. and Postman, M. (1992) The Astrophysical Journal, 400, L47. https://doi.org/10.1086/186646
[296]	Leibundgut, B. and Pinto, P. (1992) The Astrophysical Journal, 401, 49-59. https://doi.org/10.1086/172037
[297]	Birkinshaw, M., Hughes, J.P. and Arnaud, K.A. (1991) The Astrophysical Journal, 379, 466-481. https://doi.org/10.1086/170522
[298]	Tonry, J.L. (1991) Astrophysical Journal Letters, 373, L1. https://doi.org/10.1086/186037
[299]	Sandage, A. and Tammann, G.A. (1990) The Astrophysical Journal, 365, 1-12. https://doi.org/10.1086/169453
[300]	Visvanathan, N. (1990) Australian Journal of Physics, 43, 189-210. https://doi.org/10.1071/PH900189
[301]	Sandage, A. and Tammann, G. (1988) The Astrophysical Journal, 328, 1-3. https://doi.org/10.1086/166263
[302]	Dressler, A. (1987) The Astrophysical Journal, 317, 1-10. https://doi.org/10.1086/165251
[303]	Tamman, G.A. and Sandage, A. (1985) The Astrophysical Journal, 294, 81-95. https://doi.org/10.1086/163277
[304]	Visvanathan, N. (1983) The Astrophysical Journal, 275, 430-444. https://doi.org/10.1086/161544
[305]	Hanes, D.A. (1979) Monthly Notices of the Royal Astronomical Society, 188, 901-909. https://doi.org/10.1093/mnras/188.4.901
[306]	Bottinelli, L. and Gouguenheim, L. (1976) Astronomy and Astrophysics, 51, 275-306.
[307]	Sandage, A. and Tammann, G.A. (1976) The Astrophysical Journal, 210, 7-24. https://doi.org/10.1086/154798
[308]	Sandage, A. and Tammann, G.A. (1975) The Astrophysical Journal, 197, 265-280. https://doi.org/10.1086/153510
[309]	Sandage, A. and Tammann, G.A. (1974) The Astrophysical Journal, 194, 559-568. https://doi.org/10.1086/153275
[310]	Sandage, A. and Tammann, G.A. (1974) The Astrophysical Journal, 194, 223-243. https://doi.org/10.1086/153238