Validation of Numerical Modeling for the Prediction of Elastic and Failure Behavior of Diamond Powder Filled Woven Composites ()
1. Introduction
Textile structural composites are a widely used class of composites finding their applications in aerospace, automotive and manufacturing industries. They possess relatively high ratios of strain to failure in tension, compression or impact load as compared to traditional unidirectional prepreg composites [1] .
The research and developments reported in this paper have been conducted within the framework of the experiments for particle physics, such as those carried out at the Large Hadron Collider (LHC) at the European Organization for Nuclear Research (CERN). Here light-weight but very stable support structures for high precision sensors are required with the additional constraint that they need to be able to remove the heat produced from the read-out electronics and the sensors themselves. Carbon fiber reinforced composites are used in this case to provide mechanical support and protection from thermal runaway of the detector [2] . This study has been carried out to investigate the potential improvements in the elastic and failure properties of the composite materials used, with the intention of improving the mechanical behavior of the support structure of the pixel detector of the ATLAS experiment at the LHC.
Woven fabric composite laminates offer a number of attractive properties compared to their unidirectional tape counterparts. Some of these properties are, lower production costs, better drapability, good resistance to fracture and transverse rupture due to weaving resistance and high impact strength [3] . Although the mechanical properties are not as good as those of their non-woven counterparts, they still offer reasonable specific stiffness and strength with particularly good impact and energy absorption characteristics [4] . Typical failure modes of woven composites include fiber fracture, matrix fracture, fiber-matrix interface debonding and interlaminar delamination [5] [6] . The cohesive matrix fracture and adhesive fracture of the fiber-matrix interface are known as inter-fiber fracture [6] . Inter-fiber fracture is a macro type damage which starts by the initiation of matrix micro-cracks at the fiber-matrix interface during matrix curing or due to transverse stress as a result of loading, thermal stresses, or fatigue loading. The micro-cracks subsequently propagate through the matrix to form macro-cracks. In addition to the inter-fiber fracture of composites, the low failure strain and ductility are other drawbacks in the mechanical response when composites in general are loaded in fiber direction (on-axis loading) [7] . It is not uncommon that composite parts are subjected to large-deflection bending and multiple impacts in service conditions and that these quasi-static and dynamic loads generate high local stresses and strains leading to complex damage modes due to heterogeneity and anisotropy of composite laminates. In a bending scenario, a laminate experiences transverse shear and normal stresses resulting in interlaminar delamination damage, because of their low through-thickness strength and stiffness [8] . Damage evolution results in significant reduction of in-service mechanical properties and leads to a loss of structural integrity of the composite. One of the common techniques to overcome the premature failure of composites due to delamination/debonding is to reinforce the composites with fillers [3] . Carbon nanotubes (CNTs), nano-clay, graphene nanoparticles (GNPs), and nano-silica are common non-metallic nanoparticles used to fabricate nanocomposites [9] [10] . Discovered by Ijima in 1991 [11] , CNTs have attracted the attention of many scientists worldwide, because of their exceptional mechanical properties compared with conventional structural materials. Hossain et al. [12] reported a 49% and 31% increase in the flexural strength and modulus of on-axis woven E-glass/polyester composites reinforced by 0.1 - 0.4 wt% carbon nano fibers (CNF). Qiu et al. [13] examined the tensile and shear behavior of (GFRP) composites, with 1.0% by weight functionalised multi-walled carbon nanotubes (MWCNTs). It was reported that a 14% and 5% increase in on-axis tensile and shear strengths respectively was achieved. The tensile strength and modulus of the composites filled with carbon black (CB) were shown to increase with increasing filler contents but impact strength and elongation at break were reduced. It was also reported that the composites with more than 30% CB were very brittle and were difficult to mix.
Few studies have examined the use of fillers to improve thermal, tensile and failure behavior of woven fabric composites. In previous research carried out by authors, an improvement in the out of plane thermal conductivity by a factor of 2.3 and 2.8 was achieved for the standard modulus T300 and the high modulus YS90A composites filled with 14% and 12% volume fractions of DP respectively [2] . This investigation is an extension of the previous research and it has been intended to predict the mechanical and failure behavior of T300 and YS90A woven composites filled with diamond powder under tensile loading conditions. The objectives of this research were:
1) To predict the elastic properties of epoxy-diamond powder matrix through a homogenization method.
2) To develop a micromechanical unit cell model to predict the elastic properties of the diamond powder filled standard modulus T300 and the high modulus YS90A woven composites.
3) To carry out the possible experiments and the numerical models to evaluate the on-axis tensile behavior of the diamond powder filled T300 and YS90A woven composites through progressive damage modeling.
2. Homogenization of Heterogeneous Matrix Microstructure
The macro response of the epoxy-diamond powder matrix was calculated from the micro response through numerical homogenization. The mechanical properties of a micro heterogeneous matrix material were characterized by a spatially variable elasticity tensor C. Generally, in order to demonstrate the homogenized effective macroscopic response of such materials, the relation between averages are described as shown in the following:
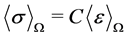 (1)
(1)
where C is defined as the effective property which is the elasticity tensor used in structural scale analysis. 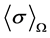 and
and 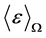 are the volume average stress and strain tensor fields within a statistically Representative Volume Element (RVE) of volume
are the volume average stress and strain tensor fields within a statistically Representative Volume Element (RVE) of volume . The two phases considered in the matrix here are epoxy (m) and diamond powder filler (d) which are denoted by volume fraction as
. The two phases considered in the matrix here are epoxy (m) and diamond powder filler (d) which are denoted by volume fraction as 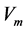 and
and . The total averaged stress and strain tensors defined by the rule of mixtures is then given by
. The total averaged stress and strain tensors defined by the rule of mixtures is then given by
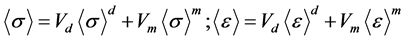 (2)
(2)
The homogenized effective elastic modulus of diamond powder filled polymer matrix composite was obtained by finite element analysis with a 2D RVE consisting of randomly distributed spherical diamond powder fillers. An algorithm as reported in the author’s previous research [2] [14] was used to generate the fillers content up to 25% volume fraction (Figure 1). The effective elastic properties of the composite were predicted from the properties of their constituents. Both the diamond powder filler and the epoxy matrix were considered to be isotropic materials with the Young’s modulus and the Poisson’s ratio given as Ed = 1000 GPa, νd = 0.2 and Em = 3.5 GPa, νm = 0.35, respectively. Python scripts were used to generate RVE’s in the commercial code ABAQUS and were meshed with 4-node bilinear plane strain quadrilateral elements with reduced integration CPE4R. Periodic boundary conditions (PBC) were then applied to the RVE. The PBC are a set of boundary conditions that are normally used when the physical geometry of interest and the expected pattern of the solutions have a periodically repeating nature. They can be used to simulate a bulk material by modeling a finite RVE [15] . For the RVE shown in Figure 1, the PBC’s were applied to the RVE to ensure a macroscopically uniform stress or displacement field for tension and shear load (Equations (3) and (4) [16] ).
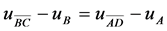 (3)
(3)
 (4)
(4)
where u is the displacement vector of any node on the boundary. The subscripts A, B, C and D correspond to the vertices. AB, BC, AD and DC correspond to the edges between the two vertices (Figure 1). The PBC’s were implemented in the form of equations using the constraint option in ABAQUS® through a python script.
PBC as Constraint Equations in ABAQUS
A general linear homogeneous equation is defined as follows
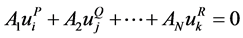 (5)
(5)
![]()
Figure 1. Representation of the periodic boundary condition in tensile (a) and shear (b) loading scenarios.
where R is the node, k is the degree of freedom and AN is a constant coefficient that defines the relative motion of the nodes [15] . In order to apply the PBC using the constraint equations as described in Equation (5), a dummy node was introduced in ABAQUS®. In Equation (5), zero on the right side of the equation would be replaced by a nonzero value
 (6)
(6)
where  is the prescribed displacement value. In ABAQUS®, the prescribed value
is the prescribed displacement value. In ABAQUS®, the prescribed value 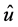 was applied through a dummy node, I, which was not attached to any other part in the model. A reference point (Figure 1) with arbitrary coordinates was defined to represent the dummy node. This node was specified as a boundary condition with the value
was applied through a dummy node, I, which was not attached to any other part in the model. A reference point (Figure 1) with arbitrary coordinates was defined to represent the dummy node. This node was specified as a boundary condition with the value 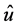 in a certain direction, as shown in Equation (7).
in a certain direction, as shown in Equation (7).
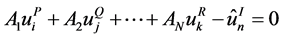 (7)
(7)
where n is the direction. A load step was defined in order to apply the prescribed displacement  as a boundary condition.
as a boundary condition.
The homogenization scheme was implemented with the volume averaged stress and strain calculated in each element to predict the effective elastic properties of the diamond powder filled polymer matrix composites. As expected, the diamond powder epoxy matrix became stiffer as the tensile and shear moduli increased with the increase in content of the diamond powder (Table 1).
3. Prediction of Elastic Properties of DP Filled Woven Composites
The prediction of the macromechanical properties of T300 and YS90A woven composites filled with diamond powder were evaluated with the periodic unit cell structure through the micromechanical method. The unit cell was modelled using TexGen [17] by considering that the warp and weft yarns posses geometric and material similarities (Figure 2). The developed geometric models together with the information of textile data (Table 2), fiber material data (Table 3) and mesh details were imported into ABAQUS® through an input file containing voxel based mesh details using 8 node 3D linear brick elements. The elastic properties of diamond powder filled polymer matrix which were predicted through numerical homogenization in the previous section (Table 1) were applied to the TexGen [17] material data for predicting the macroscopic properties
![]()
Table 1. Effective elastic properties of the DP-epoxy matrix predicted through the numerical homogenization technique.
![]()
Figure 2. FEM Model developed in TexGen with the 2/2 twill weave and the plain weave reinforcement fabrics.
![]()
Table 2. TexGen® model data for T300* and YS90A fiber**.
![]()
Table 3. T300 [18] and GRANOC YS90A [19] fiber material data.
of woven composites. The contents of the diamond powder were limited to volume fractions of 14%, 25% in epoxy corresponding to 6% and 12% by volume fraction in the composite.
The orthotropic behavior of the yarns were defined by a 3D stiffness matrix consisting of nine independent constants and are shown in Equation (10). The displacement boundary conditions for the unit cell have been defined following the procedures defined by Li et al [20] . As specified by Li et al. [20] the unit cells were treated by using the translational symmetry transformation. The macroscopic strains![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() as shown in Equation (8), were treated as six extra degrees of freedom through which loads to the unit cell have been prescribed.
as shown in Equation (8), were treated as six extra degrees of freedom through which loads to the unit cell have been prescribed.
![]() (8)
(8)
Concentrated forces were applied to these degrees of freedom and effectively, macroscopic stresses were applied to the unit cell [20] . Periodic boundary conditions were applied in the form of equations for all the unit cells that can be implemented using an equation option in ABAQUS®. Uniaxial loads (Fx, Fy, Fz, Fyz, Fxz, Fxy and ΔT) were applied to the unit cell at any point in the cell defined as constraint driven point (Figure 3) assigned as x = 0, y = 1, z = 2, xy = 3, xz = 4 and yz = 5 in the analysis to obtain the elastic properties [20] .
With the macroscopic stresses being expressed in terms of forces applied to the unit cell, the effective properties of the material represented by the unit cell were obtained in terms of the independent degrees of freedom (![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ) and the applied loads (Fx, Fy, Fz, Fyz, Fxz, Fxy and ΔT) [20] . The predicted elastic properties of T300 and YS90A composites with and without diamond powder through this micromechanical method are listed in Table 4.
) and the applied loads (Fx, Fy, Fz, Fyz, Fxz, Fxy and ΔT) [20] . The predicted elastic properties of T300 and YS90A composites with and without diamond powder through this micromechanical method are listed in Table 4.
4. Failure Behavior under Tensile and Bending
4.1. Experimental Tensile Testing
The experimental testing was only carried out for the high modulus YS90A composite filled with diamond powder in order to characterize the elastic properties of the composite filled with diamond powder under tensile loading.
![]()
Figure 3. Assigning a constraint driver point within the unit cell for applying the uniaxial loads.
![]()
Table 4. Predicted numerical elastic properties of the standard modulus T300 (55% fiber volume fraction) and the high modulus YS90A (50% fiber volume fraction)―diamond powder epoxy filled woven composites.
Twenty six layers of the plain weave fabric (On-axis 0˚ - 90˚) with an areal weight of 125 g∙m−2 relating to a fiber volume fraction of 50% were used for the fabrication of specimens. The first sample was prepared without DP and the resin mixture was infused via vacuum into the carbon fiber reinforcement fabric during the impregnation process. The remaining two samples were prepared by incorporating DP into the epoxy resin corresponding to DP volume fractions of 6% and 12% in the composite. A vacuum assisted hand layup technique was applied and the samples were cured in an autoclave at a static pressure of 24 bar for close to 9 hours. The average dimensions of the composite specimens were 200 mm long, 250 mm wide and 3 mm thick. Water-jet cutting was used to prepare coupons of 83 mm length, 15 mm width and 3 mm thickness. 1 mm thick epoxy tabs were attached to the ends of the composite coupons to facilitate adequate gripping of the specimens in the testing frame and to avoid slippage and possible failure at the grips. The on-axis tensile tests were performed (at the Institute of Composite Materials, Kaiserslautern, Germany) to examine the tensile behavior of YS90A woven composite filled without and with DP (at volume fractions of 6% and 12% in the composite). The tensile tests were performed using a SHIMADZU® Universal testing machine (Figure 4). The machine had a load cell with a capacity of 40 kN and the tests were performed at 2 mm/min following ASTM D3039 standards. In every test, load, displacement and strain were measured and recorded. The displacement was measured by the frame LVDT while the strain was measured by laser extensometer (developed and produced by Fiedler Optoeletronik GmbH) which enabled a contact free measurement of locally resolved strain distribution over the samples.
4.2. Finite Element Modeling
Numerical modeling was carried out for both the standard modulus T300 and the high modulus YS90A composites under tensile loading. Mesomechanical damage models were developed for damage detection, evolution and propagation through a progressive failure analysis methodology. Material strength, interlaminar strength and fracture toughness properties of T300 woven composite (Table 5) were taken from [21] [22] and the interlaminar strengths for the YS90A composite were examined by numerical analyses as the experimental tests to measure the strength and the fracture properties of these composites were not performed. Continuum damage mechanics models were implemented in ABAQUS® to represent the intralaminar damage modes (transverse matrix cracking and fiber failure) and cohesive elements were used to capture delamination at ply interfaces. The intralaminar and interlaminar damage models implemented are briefly described below.
4.2.1. Interlaminar Damage
Delamination is one of the typical failure modes in composite laminates due to weak bonding between fiber and polymer matrix. The constitutive response of the cohesive elements can be defined by a bilinear traction-separation law (Figure 5) which relates the nominal stress acting on the interface with the nominal strain. The cohesive elements are normally specified with unit thickness, the nominal strain corresponds to the separation value. Initially the crack is assumed to be elastic and the crack closing forces are related to the interfacial displacement jump by a high penalty stiffness (elastic modulus) Kn. The linear elasticity defines the behavior before the initiation of damage and relates the nominal stress to the nominal strain.
![]()
Table 5. T300 woven material strength [21] , interlaminar strength and toughness [22] ; YS90A material strength, interlaminar strength.
![]() (9)
(9)
The onset of damage is attained when the total stress acting on the interface reaches a critical value ![]() as given by:
as given by:
![]() (10)
(10)
where ![]() in the Equation (10) stands for Macaulay brackets which indicates that the compressive normal stress does not contribute to damage initiation and
in the Equation (10) stands for Macaulay brackets which indicates that the compressive normal stress does not contribute to damage initiation and![]() ,
, ![]() ,
, ![]() are the nominal stresses in the pure normal mode, first shear, second shear direction and
are the nominal stresses in the pure normal mode, first shear, second shear direction and![]() ,
, ![]() ,
, ![]() are the components of relative displacement between top and bottom of the cohesive element. Damage propagation leads to a progressive reduction in the stresses transferred through the interface as well as in the interface stiffness [23] . The actual reduction of the stress transferred by the cohesive crack can be defined by the slope of the softening region which depends on
are the components of relative displacement between top and bottom of the cohesive element. Damage propagation leads to a progressive reduction in the stresses transferred through the interface as well as in the interface stiffness [23] . The actual reduction of the stress transferred by the cohesive crack can be defined by the slope of the softening region which depends on ![]() and the fracture toughness GTC. The interply toughness depends on the mode-mix behavior which can be determined by the Benzeggaagh-Kenane criterion as:
and the fracture toughness GTC. The interply toughness depends on the mode-mix behavior which can be determined by the Benzeggaagh-Kenane criterion as:
![]() (11)
(11)
where ![]() is the Benzeggaagh-Kenane material parameter, GIC and GIIC are the critical fracture toughness values for pure Mode I and Mode II fracture
is the Benzeggaagh-Kenane material parameter, GIC and GIIC are the critical fracture toughness values for pure Mode I and Mode II fracture![]() ,
,![]() .
.
4.2.2. Intralaminar Damage
The constitutive stress-strain relationship are formulated in a local Cartesian coordinate system considering the base vectors aligned with the fiber directions. The fabric reinforced ply was modelled as a homogeneous orthotropic elastic material with the potential to sustain progressive stiffness degradation due to fiber/matrix cracking and plastic deformation under shear loading [23] . It has been assumed that the elastic stress-strain relationship is given by orthotropic damage elasticity. Four failure modes including fiber tension, fiber compression, matrix tension, and matrix compression are considered. Initiation of damage, which refers to the onset of damage at a material point is based on the Hashin damage model and four different failure modes based on the Hashin Criteria [24] are described in Equations (12) to (15):
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
In the above equations, ![]() are the components of the effective stress tensor, and XT and XC are the longitudinal tensile and compressive strengths, YT and YC are the tensile and compressive strengths of the matrix. SL and ST denote the longitudinal and transverse shear strengths.
are the components of the effective stress tensor, and XT and XC are the longitudinal tensile and compressive strengths, YT and YC are the tensile and compressive strengths of the matrix. SL and ST denote the longitudinal and transverse shear strengths. ![]() denotes the fiber tensile failure when
denotes the fiber tensile failure when![]() ,
, ![]() denotes the fiber compression failure when
denotes the fiber compression failure when![]() ,
, ![]() denotes the matrix tensile failure when
denotes the matrix tensile failure when ![]() and
and ![]() denotes the matrix compression failure when
denotes the matrix compression failure when![]() . The coefficient
. The coefficient ![]() in Equation (12) determines the contribution of the shear stress to the initiation of fiber tensile failure. Once the damage initiation function has been satisfied, the associated damage variable would be different from zero and further loading would cause degradation of the material stiffness coefficients [23] . The stiffness matrix of a damaged ply could therefore be defined as
in Equation (12) determines the contribution of the shear stress to the initiation of fiber tensile failure. Once the damage initiation function has been satisfied, the associated damage variable would be different from zero and further loading would cause degradation of the material stiffness coefficients [23] . The stiffness matrix of a damaged ply could therefore be defined as
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
where D as shown in Equation (18) is equal to![]() . df is the damage variable associated with fiber fracture and dm is the damage variable associated with matrix failure.
. df is the damage variable associated with fiber fracture and dm is the damage variable associated with matrix failure.
![]() (19)
(19)
ds is the shear damage variable calculated from Equation (19). The damage evolution laws for the damage variables are defined in terms of the fracture energy dissipated during the damage process. The damage evolution laws are needed to predict the material response as loading increases beyond the point of initial damage and the damage progressions are characterised by degradation of the stiffness matrix. At the point of initiation, the damage evolution model would begin to calculate the reduction in stress as the displacement of the element increases. The stress will drop until it reaches zero, the amount of displacement required to get to this point would be defined by the fracture energy, GC. In case the strength properties remain constant when the fracture energy has been increased, the element will experience a larger displacement before it reaches ultimate failure [23] .
4.2.3. Model Set-Up
Progressive failure analysis for a specimen was performed with the on-axis laminates (0˚ - 90˚) of 117 mm in length, 15 mm in width and 3 mm in thickness respectively (Figure 6). A 5-ply laminate with a ply thickness of 0.6 mm along with a cohesive layer of nearly zero thickness between each ply was modeled (Figure 6) for the tensile loading.
Each ply was modelled in ABAQUS® using quadrilateral continuum shell elements, type SC8R which is an 8-node, quadrilateral, and uses first-order interpolation with reduced integration and 3 degrees of freedom per node. Each ply was discretized by a single layer of continuum elements with reduced integration through the thickness. As the ply failure criteria and continuum damage models were derived based on the stress state of a whole ply, only a single integration point through the thickness of each ply is required. The cohesive layers between plies were modeled using COH3D8 elements which are three dimensional, 8 node (brick) cohesive elements. The ply elements were connected with the cohesive elements by using Tie constraints. The initial thickness of the cohesive elements were specified as unit thickness and a value of 1 × 106 N∙mm−3 was specified as the penalty stiffness for the interface. The interface elements were meshed with an element size of 0.5 mm. It is known that the response of cohesive elements are affected by the mesh size, however a detailed investigation of different element size towards the damage behavior was not carried out here. To alleviate the convergence difficulties, the viscous regularization option was assigned to the cohesive elements. The material data giving the elastic properties of the standard (T300) and the high modulus (YS90A) woven composite filled with diamond powder are detailed in Table 4. The strength and the toughness properties of the T300 composite (Table 5) were taken from [21] [22] .
As suggested by by H. Ullah et al. in [22] , normal and shear strengths of the YS90A composite were examined from a FEM model of an undamaged coupon under the same boundary conditions. In the numerical analysis the interlaminar
![]()
Figure 6. Finite element model representing the laminate and cohesive zone modeling for the on-axis tensile and bending.
shear stress was assumed as the interlaminar shear strength and normal stress at the ultimate load was taken as the normal strength of the laminate (Table 5). For the on-axial tensile models, fully clamped boundary conditions were applied at one end of the specimen and an uniform axial displacement was prescribed at the opposite end (Figure 6). Three different configurations of T300 and YS90A filled composite under static tension corresponding to coupons without DP and coupons with 6% and 12% DP by volume fraction in the composite, were simulated by means of an implicit numerical scheme. On average, each on-axis tensile simulation took about five hours to run on a single 3.4 GHz Intel® CoreTM i7 processor.
5. Results and Discussion
5.1. On-Axis Tensile Simulation
5.1.1. T300 Composite
The FEM results of the on-axis tensile stress-strain behavior of the standard modulus T300 woven composite with and without DP are presented in Figure 7.
The characteristics of an instantaneous load drop past the maximum tensile load would prove to be an actual case where the fiber failure occurs in all the plies almost simultaneously corresponding to the behavior of brittle failure. Fiber, matrix and the delamination damage modes are presented in Figure 8(a), Figure 8(b), Figure 9 which demonstrate the typical characteristics of brittle failure.
It can be seen that the damage initiation was faster with 6 vol % and 12 vol % DP present in the composite. From Figure 8(a) it is clear that the fiber failure occurs in all the plies. Matrix damage (Figure 8(b)) and delaminations (Figure 8(b), Figure 9) were only confined to the crack path. Overall, matrix damage in the composite has been reduced with the addition of diamond powder. With the inclusion of diamond powder, the elongation at break in the composite reduced
![]()
Figure 7. FEM results for the on-axis tensile behavior of T300- diamond powder epoxy filled composite.
![]()
Figure 8. Contour plots (a), (b) of the fiber failure (DAMEGEFT), the matrix damage (DAMEGEMT) in the standard modulus T300 composite under tension at the final failure state.
![]()
Figure 9. Contour plots showing the delamination in the standard modulus T300 composite under tension (elements were deleted upon reaching maximum degradation).
drastically (Table 6, Figure 7) as the diamond powder enhanced epoxy matrix became stiffer and more brittle. As a result of enhancing the epoxy matrix with diamond powder, the polymer viscosity, tensile modulus and tensile strength of the composite increases while the elongation at break reduces substantially, which means that high strength fillers like DP change the matrix behavior into a more rigid-like material.
5.1.2. YS90A Composite
1) Experimental tensile results
The experimental tensile testing results showed a brittle fiber fracture along with delamination. From the tensile testing, a drastic reduction in the elastic modulus and strength of the YS90A composite filled with diamond powder was observed (Figure 11, Table 7). The average ultimate tensile strength of the composite reduced to 320 MPa with 6% volume fraction of DP in the composite, while with 12% volume fraction of DP in the composite, the ultimate tensile strength reduced to 286 MPa (Figure 11). The failure strain of the composite increased to 0.56% with 12% volume fraction of DP in the composite. Elastic moduli reduced significantly to 157.7 GPa and 129.6 GPa with DP volume fractions of 6% and 12% in the composite. One of the reasons for the severe reduction in the strength and stiffness are due to the non-homogeneous dispersion (Figure 10) of the DP in the matrix.
Ultrasonication techniques were not used to achieve uniform dispersion and the manufacturing procedure was carried out by hand-layup, which led to a reduction in the production quality of the testing coupons. A higher content of diamond powder led to agglomerations and also the sharp edges of the DP itself can contribute to stress concentrations through geometric defects. A good dispersion and the interfacial properties between the epoxy resin and DP are crucial for determining the properties of the composite as the interface between the two is the region where the stresses are transferred from the epoxy resin to diamond
![]()
Table 6. On-axis tensile FEM results of the T300 composite coupons representing the modulus of elasticity (E), ultimate strength (![]() ), failure strain (
), failure strain (![]() ).
).
![]()
Table 7. Experimental results of the on-axis tension of the YS90A composite coupons representing the modulus of elasticity (E), ultimate strength (![]() ) and failure strain (
) and failure strain (![]() ).
).
![]()
Figure 10. SEM image showing non-homogeneities in dispersion of DP (marked in red) in the composite.
powder and thereby into the composite material itself. It is stated in the literature [25] that higher filler content leads to an agglomeration of particles, which reduces the adhesion between matrix and fillers and causes a drop in the mechanical strength of composites. Agubra et al. have stated that an increasing viscosity causes problems in the homogeneous dispersion of fillers and therefore results in the agglomeration of the filler particles [9] . Hossain et al. and Demirkol et al. have reported that, the non-homogeneous distribution of fillers at high filler content led to agglomeration and caused stress concentration regions, leading to some drop in the strength and modulus [26] [27] . Sobia et al. reported [28] that the mechanical properties of epoxy-diamond composites initially increased at lower contents of DP but with the higher content the mechanical properties decreased due to agglomeration. High modulus YS90A being a pitch based carbon fiber was extremely fragile to handle in terms of fabrication of the samples and the interface bonding between diamond powder-epoxy resin was not perfectly formed which can be seen from the SEM image shown in Figure 10. From the SEM image, it can be noted that, as the content of DP increased in the matrix, the DP filler network could have trapped some portion of epoxy resin preventing it from infiltrating the reinforcing fibers properly. The above hypothesis could be one of the reasons for the reduction in the tensile properties (Figure 11, Table 7) of the DP filled composite.
To understand the above mentioned behavior further, finite element modeling was performed with and without stress concentrations in the present composite specimen.
2) FEM without stress concentrations
The FEM results of the on-axis tensile behavior of the YS90A woven composite (without stress concentrations) exhibited a delamination type failure. Delamination triggered a substantial level of load drop due to dissipation of energy (Figure 11). At the ultimate tensile strength of the composite (Figure 11) just before the occurrence of massive delamination, it is worth noting that fiber failure was not detected in any of the plies (Figure 12(a)) and that matrix damage was also not present. After this point, the propagation of delamination (Figure 12(b), Figure 13) at the interface developed further. Figure 12(a), Figure 12(b) represents the damage mode occuring in the plies and demonstrates that fibers in the on-axis plies have not failed even as the load drops significantly to a level corresponding to the failure stress.
The FEM analysis of laminates without DP showed a tensile strength and
![]()
Figure 11. Comparison between the experimental tensile testing results and FEM tensile behavior without considering stress concentrations in the laminate.
![]()
Figure 12. Contour plots (a) (b) showing detection of the final fracture of the YS90A composite under tension.
![]()
Figure 13. Delamination in the interface between the plies of the YS90A composite under tension.
![]()
Table 8. On-axis tensile FEM results of the YS90A composite (without stress concentrations) representing the modulus of elasticity (E), ultimate strength (![]() ), failure strain (
), failure strain (![]() ).
).
modulus of 215 GPa and 355 MPrespectively (Figure 11, Table 8) which are in close agreement with the experimental results (Figure 11). The analysis of laminates with 6 vol % and 12 vol % of DP shows an increasing trend in the elastic modulus whereas the experimental results shows a decreasing trend due to the presence of DP induced stress concentration in the samples.
3) FEM with stress concentrations
To study the behavior of stress concentrations in the YS90A composite filled with diamond powder, Open Hole Tension (OHT) coupons were modeled with diameters of 6 mm (laminate filled with 6 vol % DP, Figure 14(a)) and 10 mm (laminate filled with 12 vol % DP, Figure 14(b)). The FEM results with the Open Hole Tensile (OHT) coupons exhibited a brittle fiber fracture (Figure 15(a), Figure 15(b)) along with delamination. The results also revealed that the presence of stress concentrations would severely reduce the stiffness and strength of the DP filled composite.Comparison of the experimental results (Figure 11) with the FEM OHT results are listed in Table 9. The FEM results with the OHT coupons predicted a reduction in the elastic modulus for the composite filled with DP (6% and 12% volume fraction) with the predictions showing reasonable accuracy when compared to the experimental results (Table 9). From the data given above, it is evident that the reduction in the elastic modulus is due to inhomogeneities in the dispersion of the DP and the presence of possible stress concentrations in the composite. The FEM results also show that a higher content of DP causes weak adhesion in the fiber-matrix interface which reduces the the strength of the composite and also reduces the ability of the composite to resist the damage (Figure 15(a), Figure 15(b), Table 9). The FEM results also show that the presence of a rigid filler reduces the elongation at the
![]()
Figure 14. Development of the OHT laminate with a diameter of 6 mm (a) and 10 mm (b) for studying the behavior of stress concentrations under tensile loading.
![]()
Figure 15. Fiber failure under tension for the YS90A composite with stress concentrations modeled with OHT coupons.
![]()
Table 9. Comparison of the experimental tensile and FEM-OHT results of the on-axis tension of the YS90A composite representing the modulus of elasticity(E), ultimate strength(![]() ) and failure strain (
) and failure strain (![]() ).
).
break (Table 9). In general, the elastic and the failure properties reduce significantly with the presence of stress concentrations. The drastic increase in the failure strain (Table 9, Figure 11) as shown by the experimental results for the composite filled with 12% volume fraction of DP requires further investigation.
6. Conclusions
In this study, the elastic and failure characteristics of standard modulus T300 and high modulus YS90A woven composites filled with diamond powder were examined. A numerical homogenization technique was applied to predict the elastic properties of the diamond powder enhanced matrix. Micromechanical unit cell models were first developed to predict the elastic properties of the diamond powder filled woven composites. Finite element modeling was then carried out to predict the failure behavior of the composite under tension. From the on-axis FEM simulations, it was observed that with the addition of DP, elongation at break in the composite reduced drastically as the DP filled epoxy matrix became stiffer and more brittle.
Fabrication of the YS90A composite through the matrix modification technique with DP led to agglomeration. An inhomogeneous dispersion of the diamond powder in the composite was observed from SEM images. This eventually reduced the elastic properties of the YS90A composite when subjected to on-axis tensile testing. Finite element modeling of the YS90A composite was carried out with OHT coupons to investigate the effect of stress concentrations in the composite when subjected to tensile loading. A reduction in the elastic modulus was observed with the OHT FEM results.
Ultrasonic dispersion technique to overcome the problem of an inhomogeneous dispersion of diamond powder in the composite must be explored and investigated. Furthermore, experimental testing must be carried out to examine the interfacial shear strength and stiffness of the diamond powder filled woven composites.
A detailed investigation of the mesh sensitivity towards the predicted damage behavior must also be carried out. Different constitutive laws considering through the thickness mechanical properties as well as strain rate effects in the diamond powder filled composite are required and need to be developed which could be implemented through an explicit rather than implicit FEA modeling scheme.