Existence and Uniqueness of Solution for Cahn-Hilliard Hyperbolic Phase-Field System with Dirichlet Boundary Condition and Regular Potentials ()
1. Introduction
G. Caginalp introduced in [1] the following phase-field system
 (1)
(1)
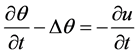 (2)
(2)
where u is the order parameter and 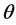 is the (relative) temperature. These equations model phase transition processes such as melting-solidification processes and have been studied, see [2] - [6] , for a similar phase-field model with a nonlinear term.
is the (relative) temperature. These equations model phase transition processes such as melting-solidification processes and have been studied, see [2] - [6] , for a similar phase-field model with a nonlinear term.
These Cahn-Hilliard phase-fiel system are known as the conserved phase-field system (see [7] - [9] ) based on type III heat conduction and with two temperatures (see [10] ). The authors have proved the existence and the uniqueness of the solutions, the existence of global attractor and of exponential attractors with singularly or regular potentials.
In [11] , Ntsokongo and Batangouna have studied the following Cahn-Hilliard phase- field system
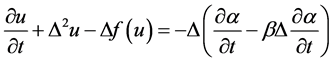 (3)
(3)
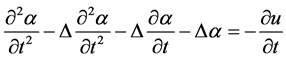 (4)
(4)
where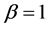 , u is the order parameter and
, u is the order parameter and  is the (relative) temperature, they have proved the existence and the uniqueness solution with Dirichlet boundary condition and regular potentials.
is the (relative) temperature, they have proved the existence and the uniqueness solution with Dirichlet boundary condition and regular potentials.
In this paper, we consider the following Cahn-Hilliard hyperbolic phase-fiel system
 (5)
(5)
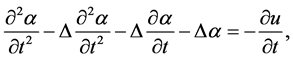 (6)
(6)
 (7)
(7)
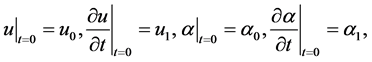 (8)
(8)
which is the perturbed phase-field system of Cahn-Hilliard phase-field system (3)-(4) with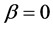 . In the above hyperbolic system
. In the above hyperbolic system 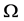 is a bounded and regular domain of
is a bounded and regular domain of 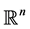 with
with 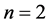 or 3 and f is the nonlinear regular potentials.
or 3 and f is the nonlinear regular potentials.
The hyperbolic system has been extensively studied for Dirichlet boundary conditions and regular or singular potentials (see [12] - [14] ). Whose certain have to end at existence of global attractor or at the existence of exponential attractors (see [15] ).
In this paper we prove the existence and the uniqueness of solutions of (5)-(8). We consider the regular potential 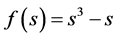 which satisfies the following properties:
which satisfies the following properties:
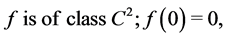 (9)
(9)
 (10)
(10)
![]() (11)
(11)
2. Notations
We denote by ![]() the usual L2-norm (with associated product scalar (.,.)) and set
the usual L2-norm (with associated product scalar (.,.)) and set
![]() , where
, where ![]() denotes the minus Laplace operator with Dirichlet
denotes the minus Laplace operator with Dirichlet
boundary conditions. More generally, ![]() denote the norm of Banach space X.
denote the norm of Banach space X.
Throughout this paper, the same letters ![]() and
and ![]() denote (generally positive) constants which may change from line to line, or even a same line.
denote (generally positive) constants which may change from line to line, or even a same line.
3. A Priori Estimates
We multiply (5) by ![]() and (6) by
and (6) by![]() , integrate over
, integrate over ![]() and add the two resulting differential equalities. We find
and add the two resulting differential equalities. We find
![]()
where
![]()
satisfies
![]()
Finaly, we conclude that![]() ,
,
![]()
and
![]()
for all![]() .
.
Multiply (6) by ![]() and integrate over
and integrate over![]() . We get.
. We get.
![]()
![]()
Then![]() .
.
In this study, we have three main results; existence theorem, uniqueness theorem and existence theorem with more regularity.
4. Existence and Uniqueness of Solutions
Theorem 4.1. (Existence) We assume ![]() then the system (5) - (8) possesses at least one solution
then the system (5) - (8) possesses at least one solution ![]() such that
such that
![]() ,
,
![]() ,
,
![]()
and![]() , for all
, for all![]() .
.
The proof is based on a priori estimates obtained in the previous section and on a standard Galerkin scheme.
Theorem 4.2. (Uniqueness) Let the assumpptions of Theorem 4.1 hold. Then, the system (5) - (8) possesses a unique solution ![]() such that
such that
![]() ,
,
![]() ,
,
![]()
and ![]() for all
for all![]() .
.
Proof. Let ![]() and
and ![]() be two solutions of the system (5)-(8) with initial data
be two solutions of the system (5)-(8) with initial data ![]() and
and![]() , respectively. We set
, respectively. We set ![]() and
and![]() , then
, then ![]() is solution of the following system
is solution of the following system
![]() (12)
(12)
![]() (13)
(13)
![]()
![]()
![]()
We multiply (12) by ![]() and integrate over
and integrate over![]() . We find
. We find
![]() (14)
(14)
Multiplying (13) by ![]() and integrating over
and integrating over![]() , we get
, we get
![]() (15)
(15)
Now summing (14) and (15) we obtain
![]() (16)
(16)
where
![]()
Lagrange theorem gives a estimates
![]()
which implies
![]()
Inserting the above estimate into (16), we have
![]()
Applying Gronwall’s lemma, we obtain for all ![]()
![]()
We deduce the continuous dependence of the solution relative to the initial conditions, hence the uniqueness of the solution.
The existence and uniqueness of the solution of problem (5)-(8) being proven in a larger space, we will seek the solution with more regularity. ![]()
Theorem 4.3. Assume
![]() ,
,
then the system (5)-(8) possesses a unique solution ![]() such that
such that
![]() ,
,
![]() ,
,
![]() ,
,
![]()
and![]() , for all
, for all![]() .
.
Proof. Following theorems 4.1 and 4.2, the system (5)-(8) possesses the unique solution ![]() such that
such that
![]() ,
,
![]() ,
,
![]()
and![]() , for all
, for all![]() .
.
Multiply (2.1) by ![]() and integrate over
and integrate over![]() . We have
. We have
![]()
we deduce the following inequality
![]() (17)
(17)
Thanks to use![]() , we find the following estimate
, we find the following estimate
![]()
Since![]() , then the estimate (17) implies
, then the estimate (17) implies
![]() (18)
(18)
Multiplying (6) by ![]() and integrating over
and integrating over![]() , we get
, we get
![]() (19)
(19)
Now summing (18) and (19), we obtain
![]()
where
![]()
Appling the Gronwall’s lemma, we deduce that![]() ,
,
![]()
and
![]() .
.
Multiplying (5) by ![]() and integrating ovre
and integrating ovre![]() , we obtain
, we obtain
![]() (20)
(20)
Thanks to use ![]() and the fact that
and the fact that![]() , we get
, we get
![]()
Inserting the above estimate into (20), we obtain
![]()
which implies that![]() .
.
Multiplying (6) by ![]() and integrating over
and integrating over![]() , we find
, we find
![]()
that implies![]() .
. ![]()
5. Conclusion
We have just shown the theorems of existence and uniqueness of the solutions for perturbed Cahn-Hilliard hyperbolic phase-field system with regular potentials.