A Stochastic SIVS Epidemic Model Based on Birth and Death Process ()
1. Introduction
Recently, a great interest in the analysis and prediction of consequences of public health strategies designed to control infectious disease, particularly tuberculosis and (Acquired Immune Deficiency Syndrome) AIDS [1] , has arised. The epidemic model includes vaccination and is referred to as an (Susceptible-Infected-Vaccinated-Susceptible) SIVS epidemic model, where the classes contain susceptible, infective, and vaccinated in- dividuals [1] [2] . The deterministic model was analyzed by Christopher M. Kribs-Zaleta [3] . Transmission and control of infections disease are affected by many uncertain factors, then become a stochastic process. Trend of the spread of the disease is usually only with a certain current state. That is to say, under certain conditions, each class number changes is the nature of the Mrakov process.
Birth and death process [4] is a kind of important and wide application of Markov process, the theoretical results are systematical, mature and in-depth. But various studies focused on the birth and death process itself, few people use it. Birth and death process in random environment have been researched by L. J. S. Allen and P. S. Mandal [5] [6] .
Plentful well-known stochastic epidemic models have been used to investigate questions regarding the dynamics of an epidemic [7] - [13] . There are many studies have been investigated using stochastic models [8] [14] . Our goal in this investigation is to compare the dynamics of the deterministic and the stochastic epidemic model. The stochastic models are a continuous-time Markov chain model and a stochastic dif- ferential equation model [4] [14] [15] . The stochastic differential equation model is a new formulation that is derived from the Markov chain model.
In this paper, the continuous time Markov chain model and the stochastic dif- ferential equation model based on birth and death process [4] [14] [16] are formulated based on the deterministic epidemic model. We use the cumulative generating function to express the moment equation of the numerical characteristics of random variables and Itô stochastic differential equation [4] [14] [16] of continuous time and discrete state. In addition, at the disease-free equilibrium, it is shown that the expected values of the random variables agree with the solution to the deterministic model. Finally, through extensive numerical simulations, the comparison of deterministic model and stochastic model is given.
2. Deterministic Epidemic Model
Consider a model for an (Susceptible-Infected-Susceptible)SIS disease where a vacci- nation program is in effect, which was analyzed by C. M et al. [3] . The model consists of three differential equations, one for each of the three disease states: susceptible, infective, and vaccinated, with the number in each class denoted by S(t), I(t), and V(t), respectively. The system of differential equations for the deterministic epidemic model is
 (1)
(1)
where N is the constant total population size; thus we can reduce the size of the model by letting 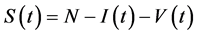 and get the new model as
and get the new model as
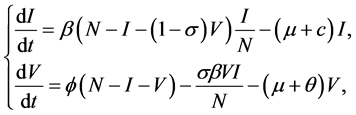 (2)
(2)
note that the parameters are all non-negative, and  is the transmission rate,
is the transmission rate, 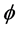 is the vaccination rate,
is the vaccination rate, 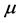 is the natural death or birth rate, c is the recovery rate,
is the natural death or birth rate, c is the recovery rate,  is the rate of vaccine waning. The vaccine is assumed to be useful but imperfect. Thus the vaccine efficacy denoted by
is the rate of vaccine waning. The vaccine is assumed to be useful but imperfect. Thus the vaccine efficacy denoted by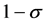 ,
,  measures the efficiency of the vaccine as a multiplier to the infection rate: when
measures the efficiency of the vaccine as a multiplier to the infection rate: when , vaccination is hundred percent effective; and when
, vaccination is hundred percent effective; and when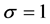 , the vaccine is totally useless.
, the vaccine is totally useless.
Although model (1) can well describe the development of the disease, in the spread and control of disease there still exist some uncertain factors such as temperature, environment of the hospital symptomtesting, etc. And the effect produced by these factors is particularly important. Based on the deterministic model (2) after dimension reduction, we take the influence of random factors on the spread of disease into considering, and establish the continuous time Markov chain (CTMC) model, namely the birth and death process.
3. The Birth and Death Process under CTMC
In this section, we construct a CTMC model under birth and death view for the epi- demic model based on the ordinary differential equation model (2). Let 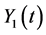 and
and 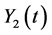 denote the discrete random variables for the number of infected and vaccinated cells at time t, the random variables
denote the discrete random variables for the number of infected and vaccinated cells at time t, the random variables 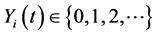 and
and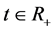 ,
, . Let the initial values be fixed,
. Let the initial values be fixed, 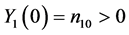 and
and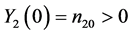 . The corresponding pro- babilities associated with the bivariate process
. The corresponding pro- babilities associated with the bivariate process ![]() are as follows:
are as follows:
![]() (3)
(3)
where![]() ,
,![]() . Set
. Set ![]() and
and ![]() be sufficiently small such that
be sufficiently small such that ![]() for
for![]() . We formulate the continuous time Markov chain model as a birth and death process in each of the variables [4] . When time is sufficiently small, there is
. We formulate the continuous time Markov chain model as a birth and death process in each of the variables [4] . When time is sufficiently small, there is
![]() (4)
(4)
where![]() ,
, ![]() ,
, ![]() ,
,
![]() . The probabilities
. The probabilities ![]() satisfy the forward
satisfy the forward
Kolmogorov differential equation [4] . Then, we have
![]() (5)
(5)
where ![]()
In addition, when![]() , we have
, we have
![]() (6)
(6)
where ![]()
When![]() , we have
, we have
![]() (7)
(7)
where ![]() For
For![]() , there is
, there is
![]() (8)
(8)
The moment of the distribution corresponding to the bivariate process can be derived directly from the preceding forward Kolmogorov differential equation. The form of the moment generating function is
![]() (9)
(9)
for some![]() , the moment generating function is a solution of the partial differential equation by follows [4] [17] [18] :
, the moment generating function is a solution of the partial differential equation by follows [4] [17] [18] :
![]() (10)
(10)
By applying the product rule for differentiation, and differentiating both sides of the preceding differential Equation (10) with respect to![]() , we get
, we get
![]() (11)
(11)
Take ![]() in Equation (10), the equations for expectation of
in Equation (10), the equations for expectation of ![]() is:
is:
![]() (12)
(12)
Differentiating both sides of the preceding differential Equation (10) with respect to![]() , it shows that
, it shows that
![]() (13)
(13)
Equation (10) then gives the following differential equations for the expectation of ![]() by substituting
by substituting![]() :
:
![]() (14)
(14)
From all of the above, we get
![]() (15)
(15)
To enlarge type on the right side, it follows that
![]() (16)
(16)
Take
![]() (17)
(17)
then
![]() (18)
(18)
This represents that ![]() and
and ![]() are constrained by certain conditions, so the ex- pectations of the random variables lie in the region
are constrained by certain conditions, so the ex- pectations of the random variables lie in the region
![]() (19)
(19)
For the above![]() , the number of infected and vaccinated also lies in this region. And the set
, the number of infected and vaccinated also lies in this region. And the set
![]() (20)
(20)
is invariant. Therefore, the expectations have the same property as the variables in the deterministic model.
4. Itô Stochastic Differential Equations
Based on the CTMC model, Itô SDEs can be derived by applying the methods in [17] [19] . The possible changes of CTMC model are given in Table 1, similar to the Markov chain model.
Let ![]() and
and ![]() denote continuous random variables for the side of I and V, respectively. Then
denote continuous random variables for the side of I and V, respectively. Then ![]() is a vector random variable defined on an appropriately defined sample space, where
is a vector random variable defined on an appropriately defined sample space, where
![]() (21)
(21)
As in the CTMC model, it is assumed that the time interval ![]() is sufficiently small, so that at most one birth or death occur in this time interval. Let
is sufficiently small, so that at most one birth or death occur in this time interval. Let ![]() , where
, where![]() ,
,![]() . The ith change is denoted by
. The ith change is denoted by![]() . Terms
. Terms ![]() are neglected. For sufficiently small
are neglected. For sufficiently small![]() , the expectation vector of
, the expectation vector of ![]() is
is
![]() (22)
(22)
In addition, the variance of![]() ,
, ![]() is defined as
is defined as ![]() , then the covariance of
, then the covariance of ![]() and
and ![]() is
is ![]() . The covariance matrix for
. The covariance matrix for ![]() is
is
![]() (23)
(23)
where ![]() is neglected since it is
is neglected since it is![]() .
.
![]() (24)
(24)
hence
![]() (25)
(25)
where![]() . In addition, we also have
. In addition, we also have
![]() (26)
(26)
for![]() . Therefore, the covariance matrix
. Therefore, the covariance matrix ![]() can be approximated as follows [19] :
can be approximated as follows [19] :
![]() (27)
(27)
For sufficiently small ![]() and large
and large![]() ,
, ![]() has an approximate normal distribution with mean
has an approximate normal distribution with mean ![]() and covariance matrix
and covariance matrix![]() , where
, where![]() , see [15] [19] . Let
, see [15] [19] . Let![]() . Then there is
. Then there is ![]() and the approximation to
and the approximation to![]() :
:
![]() (28)
(28)
Due to that the preceding expression is an Euler-Maruyama approximation to a system of Itô stochastic differential equation [20] , that is to say, the system (28) can converge in the mean square sense to the system of Itô stochastic differential equation as follows:
![]() (29)
(29)
where ![]() and B mean the drift term and the diffusion matrix, respectively. Thereby the system can be represented by the following formula:
and B mean the drift term and the diffusion matrix, respectively. Thereby the system can be represented by the following formula:
![]() (30)
(30)
where ![]() and
and ![]() are two independent Wiener processes.
are two independent Wiener processes.
Note 1: The form of the Itô stochastic differential equation is not unique. From the reference [18] , the form of Equation (30) can be expressed in other ways as the equivalent stochastic differential equations with the same joint probability density like
![]() (31)
(31)
where ![]() and
and
![]() (32)
(32)
with ![]() a vector of four independent Wiener process [4] [19] and it represent independent standard Brownian motion respectively.
a vector of four independent Wiener process [4] [19] and it represent independent standard Brownian motion respectively.
Note 2: Birth and death rates can be varied in forms. In the preceding formulations, we have assumed that the per capita birth and death rates of the population are positive and negative, respectively. In fact, we can take the birth and death rates from the Itô stochastic differential equation.
For example, let
![]() (33)
(33)
where ![]() and
and ![]() are positive constants,
are positive constants, ![]() , and satisfy the following re- lations:
, and satisfy the following re- lations:
![]() (34)
(34)
for redefined ![]() and
and![]() , we can get the following Itô stochastic differential equation by a similar method.
, we can get the following Itô stochastic differential equation by a similar method.
![]() (35)
(35)
it is clear that the terms in the Wiener processes of the Itô stochastic differential equation are greater in model (35) since![]() ,
, ![]() for
for![]() .
.
5. Numerical Simulation
Numerical simulations are used to illustrate the dynamics of the deterministic model, continuous time Markov chain model and stochastic differential equation model. We simulate the birth and death process perspective of infectious disease model by ap- plying MATLAB. Throughout the paper, we choose the parameters as:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . Take initial values
. Take initial values![]() . The stable equilibrium in the deterministic model is
. The stable equilibrium in the deterministic model is ![]() which is a global attractor.
which is a global attractor.
Figure 1(a) and Figure 1(b) respectively display two sample paths of the stochastic model graphed with the ordinary differential equation. It can be clearly seen from the dashed line in Figure 1 that with the change of time, infected number are gradually
increased and close to the equilibrium value. At the same time, vaccinated number are gradually reduced. One sample path for the stochastic differential equation models (30) and (35) is graphed in Figure 1(a) and Figure 1(b) with the solid line. Figure 1 shows the solution of the stochastic model fluctuates around the solution of deterministic model due to weak noise intensities which reflects that the disease will persistent.
At t = 1000, 15,000 sample paths are used to compute probability histograms for the stochastic equation models (30) and (35). The initial conditions lie in the basin of attraction for the stable endemic equilibrium for the deterministic model is ![]() . The two models of the probability distributions are visible in Figure 2(a) and Figure 2(b). The graphs in Figure 2(a) and Figure 2(b) are computed from the CTMC model.
. The two models of the probability distributions are visible in Figure 2(a) and Figure 2(b). The graphs in Figure 2(a) and Figure 2(b) are computed from the CTMC model.
The number of infected people is represented by the horizontal axis and vaccinated people is represented by the vertical axis. A two-dimensional random walk is given in Figure 3. It’s easy to see the path of the random walk around the equilibrium point![]() .
.
6. Conclusions
In this paper, two new stochastic epidemic models, namely, a continuous time Markov model and a stochastic differential epidemic model, are formulated to account for the variability inherent in the birth, death, and infection process. Our goals are to provide the solution of the stochastic model and CTMC model fluctuates around the endemic disease equilibrium![]() , and the average fluctuations around the endemic disease equilibrium
, and the average fluctuations around the endemic disease equilibrium ![]() in time are small due to the weak noise intensities. Furthermore, we get the path of the random walk of infected number and vaccinated number also
in time are small due to the weak noise intensities. Furthermore, we get the path of the random walk of infected number and vaccinated number also
around the equilbrium point.
The continuous time Markov chain model is preferred over the stochastic differential equation model because the continuous time Markov chain model preserves the discrete population values. We also derived the formula for the fluctuation of the solution around the endemic equilibrium and obtained the ergodicity of the stochastic model. Computer simulations are presented to verify our theoretical results. Based on the parameter value, simulations of the CTMC model show for a population size N = 500 and depending on the initial values, introduction of a small number of infective individuals into a population can have similar long term outcomes in the stochastic model. We found that weak noise intensities affect long term behavior of each state slightly. These results regarding population size and choice of deterministic versus stochastic model apply to the pertussis model but may hold for more general epidemic models when the population is homogeneously mixed.
Acknowledgements
We are grateful to the editor and referees for their valuable comments that greatly improved the presentation of this paper.