A New Lung Mechanics Model and Its Evaluation with Clinical Data ()
1. Introduction
Acute Respiratory Distress syndrome (ARDS) is a major cause of morbidity and has a high mortality (between 20% and 50%) [1]. ARDS can be triggered by various conditions such as trauma, pneumonia or sepsis. Mechanical ventilation (MV) is a life saving treatment for many patients in the intensive care unit (ICU) [2]-[4]. Especially, patients with acute lung injury (ARDS and others), suffering from lung failure, need to be mechanically ventilated for breathing support. But there is no golden rule or protocol for mechanical ventilation in the treatment of ARDS patients. Especially these patients exhibit diverse conditions and a heterogeneous distributions of healthy and diseased alveoli in their lungs, thus a patient-specific protocol is necessary to choose optimal settings of MV [5] [6] (in particular positive end expiratory pressure (PEEP) levels). However, inappropriate settings of MV can lead to ventilator induced lung injury (VILI) [7] [8]. An optimal solution would choose the best initial parameters and adjust them continuously during the treatment to optimize the therapy for each patient [9]. This goal can be achieved with a model-based approach that can assimilate the various MV standards. This approach allows patient-specific parameter identification and thus the reduction of the risk of lung injury during MV. However, for a lung model to be successful it should not require additional measurement equipment in ICU. While there are many models developed for this purpose [10]-[16], not many of them are able to fit all ventilation modes. This study introduces a new lung model which is based on the non-linear autoregressive (NARX) model previously presented by Langon et al. [17]. This new modified NARX model (mNARX model) consists of a pressure dependent elastance term and a pressure dependent resistance term and both terms were modeled via basis functions.
2. Material and Methods
2.1. Patient Data
The data were measured between 2000 and 2002 in the intensive care units of eight German hospitals [18] and a total of 28 patient’s measurements were taken. These patients suffered from acute lung injury or ARDS and the protocol was approved by local ethics committee of each participating institution. All patients were mechanically ventilated for more or equal to 24 hours before the study entry. Airway pressure was measured by a piezo resistive pressure transducer; flow was measured using a pneumo- tachograph connected to a differential pressure transducer. Volume-controlled ventilation was used with a constant inspiratory flow rate, the tidal volume of 8 ± 2/kg and the PaCO2 < 55 mmHg were maintained before the measurements. The patients were ventilated with zero end expiratory pressure (ZEEP) for 5 minutes, having an end-inspira- tory pause of ≥0.2 seconds and afterwards the PEEP level was increased in steps of 2 cm H2O―each PEEP level was kept constant for 10 breathing cycles. The volume was calculated through continuous integration of the flow with adjustment for volume creep. The data sampling rate was 62.5 Hz. Full details of the original study can be found in Stahl et al. (2006) [18]. In our study the NARX model and mNARX model were applied to 25 of these patient data sets, according to Langdon et al. [19] the other 3 datasets have been excluded from this analysis, because they showed highly nonlinear behavior.
2.2. Lung Mechanics Models
2.2.1. First Order Model
The simplest pulmonary model to describe the human lungs is a first order model (FOM). The FOM simplifies the lung as being one compartment with a constant airway resistance and constant lung compliance. The behavior of the FOM can be expressed by Equation (1).
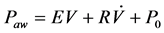 (1)
(1)
where Paw is airway pressure,  is airway flow rate, E is pulmonary elastance, V is the inspired volume and P0 is the offset pressure.
is airway flow rate, E is pulmonary elastance, V is the inspired volume and P0 is the offset pressure.
2.2.2. Non-Linear Autoregressive Model (NARX)
Langdon et al. (2015) proposed a non-linear autoregressive model (NARX) of the pulmonary mechanics, based on an FOM. This NARX model determines the input-output relationship of the system and thus can predict the pressure volume relationship, based on previous inputs. It consists of a pressure dependent elastance term and a multi-valued resistance term that captures changes in pressure.
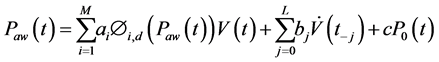 (2)
(2)
where ai, bj and c are parameters to be identified, M the number of basis-functions Φi,d (Paw(t)) of degree d, V(t) is the inspired volume, L is the length of the resistance vector, j is the index of the resistance vector and  is airway flow rate.
is airway flow rate.
Zeroth and higher order basis functions are defined as:
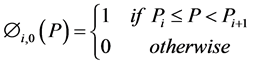 (3)
(3)
 (4)
(4)
2.2.3. Modified Non-Linear Autoregressive Model
The modified NARX (mNARX) model was built on the basis of the NARX model by replacing the multi-valued resistance term by a pressure dependent resistance via the use of basis functions. The modified NARX model was defined as:
 (5)
(5)
where ai are the coefficients for the basis functions that represents the elastance terms, M the number of elastance basis functions Φi,d(Paw(t)) of degree d, bj are the resistance coefficients that represent the resistance terms, L the number of the pressure dependent resistance basis functions ∏j,d(Paw(t)) of degree d.
Zeroth and higher order basis functions are defined as:
 (6)
(6)
 (7)
(7)
 (8)
(8)
 (9)
(9)
2.3. Model Class Selection
Though the final goal was to identify the parameters ai (elastance coefficients), bj (resistance coefficients) and c (offset or initial pressure), first the optimum number (M) of basis functions for the elastance term, the number (L) of basis functions for the resistance term and their order (d) had to be determined. Therefore the mNARX model was applied to 25 data sets and by varying the values of M, L and d, this parameters were determined via analyzing the fit of the model. First, the optimal value of L was selected, followed by d and finally M. To get the optimal value for L, it was varied until convergence of the root mean squared (RMS) residuals was achieved. In the case of d, cumulative distribution function (CDF) plots were determine to find significant differences between the residuals. Finally, the optimal value of M was determined as a tradeoff between improving residuals and avoidance of over fitting.
3. Results
The value of L was varied from 1 (in steps of 10) until a convergence was achieved, with constant values for M = 5 and d = 1. Convergence was assumed when the root mean squared residual stopped improving by more than 0.5% of the previous value. Figure 1(a) and Figure 1(b) shows the RMS pressure residual for patient 2, NARX with L = 1, 100 and 342 (converged values) and mNARX with L = 2, 5 and 20. Figure 1(c) and Figure 1(d) illustrates the significant decrease of the RMS pressure residual with increase in L values for both the models. The peaks in Figure 1(d) indicate the poor performance of the model for low values of L. The order of basis functions d was varied (d = 0, 1 and 2), with L (the gained converged value) and M = 5 the RMS residuals were calculated.
Figure 2(a) and Figure 2(b) shows the empirical CDF’s for the residuals of patient 10. The number of the basis functions was varied (M = 2, 5, 10 and 15) using constant values for d = 1 and L (respective converged value). In the NARX model an average decrement of 5.4% in residuals between M = 2 and M = 5, 3% between M = 5 and M = 10 and finally 1.5% between M = 10 and M = 15 could be observed. Similarly, in the mNARX model: 3.9% between M = 2 and M = 5, 1.2% between M = 5 and M = 10, and 0.6% decrement between M = 10 and M = 15. The RMS residual changes were minimal―hence, the elastance coefficients were also taken into consideration. Figure 2(c) and Figure 2(d) show the plot of ai coefficients for patient 1, the elastance coefficients in ARDS patients are expected to be smooth and curve due to lung characteristics (such as recruitment phases and overdistention during different PEEP levels). Figure 2(c) and Figure 2(d) show that the elastance coefficients become more unstable for M > 5, hence the numbers of basis functions for both the models were promising for M = 5. The final structure for NARX and mNARX was formulated with the parameters which showed the best results. Table 1 shows the optimal parameter values for the final selection and formulation of the models.
Pressure Identification in Case of Missing Data
The parameters of the NARX and the mNARX model were identified by using the first 4 and the last 4 different PEEP levels―the remaining data (approx. 5 different PEEP levels) was used to evaluate the model performance assuming missing data. Figure 3(b) shows the RMS residual for NARX, mNARX and FOM calculated from evaluated data.
4. Discussion
The NARX model and mNARX model fit all the 25 patients successfully and both the models were able to describe all the parts of the breathing cycle. The outcomes of the NARX and mNARX models were compared with the outcome of the FOM. The model fit during the inspiratory pause and expiratory relation were promising in NARX and mNARX, while the FOM failed to describe all parts of the breathing cycle in higher PEEP-levels. Figure 1 showed that there was a significant decrease of the RMS residuals with increase in L and poor modeling with low values of L. In the NARX model, L was used as the length of the resistance vector (L = 350)―whereas, in the mNARX model L represented the number of pressure dependent basis functions. Using L = 20 (mNARX) allowed to fit all 25 data sets with minimal RMS residuals. Regarding d, first order basis functions were used for both models, due to the improved results of 8.84% (NARX model) and 3.8% (mNARX model) between zeroth and first order basis functions. Figure 2(a) and Figure 2(b) show this significant difference in the NARX model between zeroth and first order basis functions and negligible changes between first and second order basis functions. Furthermore, in Figure 1 it can be seen, that zeroth order basis functions are not sufficient to capture the complex behavior of ARDS patients. RMS
![]()
Table 1. Final structure of NARX and mNARX model.
![]()
![]()
Figure 3. Parameter identification data (blue) and evaluation data (red) (left). RMS residuals for NARX, mNARX and FOM calculated via evaluated data (right).
residuals showed improved results between zeroth and first order basis functions, while the usage of second order basis functions didn’t show worthwhile improvements. Hence, first order basis functions were sufficient for both models. The elastance coefficients in ARDS patients are expected to be smooth and curve due to the lung characteristics of ARDS patients such as recruitment phases and overdistention during different PEEP levels. Figure 2(c) and Figure 2(d) show the elastance coefficients for M = 2 - it is just a straight line and limits the basis functions to describe the recruitment phases between different PEEP levels. Similarly, for M > 5 the ai coefficients becomes unstable and doesn’t allow predicting the future and past PEEP levels. Hence, the number of basis function for both the models was set to M = 5. Figure 3(b) shows the predictive behavior of NARX and mNARX models when some parts of the clinical data are missing.
A limitation for the prediction behavior of NARX and mNARX is that the range of identification pressure should cover the entire range of interpolation. A multiple and broad range of steps were undertaken to evaluate both models to find the optimal values of their final structure. A broad range of clinical conditions and ventilation modes were applied to both models to capture the different behavior and the obtained results enabled us to interpret and compare the models. Figure 4 showed that the NARX model can be more complex, a higher dimension of the resistance vector could possibly lead to overfitting compared to the mNARX model. Overall both the models were able to model all the parts of the breathing cycle successfully, however considering noise the mNARX model performed better than the NARX.
5. Conclusion
In this study a new lung mechanics model was introduced. The multivariate process was undertaken to determine the optimal parameters for the final structure of the mNARX model. The model was able to fit all 25 patient data sets and successfully describe all the parts of the breathing cycle. The model was highly successful in predicting missing data with minimal error compared to the FOM. Hence, this model could be
![]()
![]()
Figure 4. Example of overfitting of noise (left) NARX and (right) mNARX.
used by the clinicians to optimize patient specific ventilator settings. Further improvements of the model could be done by investigating the order of the basis functions of the resistance term which was not evaluated in this study.