On the Theory of Fractional Order Differential Games of Pursuit ()
Received 15 July 2016; accepted 19 August 2016; published 22 August 2016

1. Introduction
The dynamics of the systems described by the equations of fractional order is the subject of research experts from around the middle of the XX century. The study of dynamical systems with fractional order management is actively developing in the last 5 - 8 years [1] [2] . The growing interest in these areas is due to two main factors. Firstly, by the middle of the last century it has been adequately worked out the mathematical foundations of fractional integro-differential calculus and the theory of differential equations of fractional order. Around the same time, it began to develop a methodology and application of fractional calculus in applications, and we started to develop numerical methods for calculating integrals and derivatives of fractional order. Secondly, in fundamental and applied physics by this time, it had accumulated a considerable amount of results, which showed the need for fractional calculus apparatus for an adequate description of a number of real systems and processes [3] . Examples of real systems will mention electrochemical cells, capacitors fractal electrodes, the viscoelastic medium. These systems have typically not trivial physical properties useful from a practical standpoint [4] - [7] . For example, the irregular structure of the electrodes in capacitors allows them to reach a much larger capacity, and the use of electrical circuits with elements having a transfer characteristic of fractional- power type, provides more flexible configuration of fractional order controllers used in modern control systems. For such control systems of fractional order as of today, there are no similar results Pontryagin type [8] - [11] .
2. Methods
Let driving of object in a finite-dimensional Euclidean space of 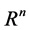 be described by a differential equation of a fractional order of a look
be described by a differential equation of a fractional order of a look
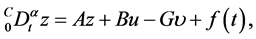 (1)
(1)
where 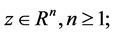
 ―operator of fractional derivation,
―operator of fractional derivation, 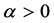 ,
, 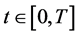 ,
,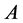 ―
―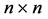 ,
, ―
―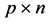 and
and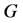 ―
―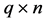 constant matrixes,
constant matrixes,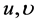 ―the operating parameters,
―the operating parameters,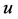 ―the operating parameter of the pursuing player,
―the operating parameter of the pursuing player, 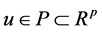 ,
,![]() ―the operating parameter of the running-away player,
―the operating parameter of the running-away player, ![]() ,
, ![]() and
and ![]() - compact,
- compact, ![]() -known measurable vector function. We will understand a fractional derivative as left-side fractional derivative Kaputo [1] - [6] . Let’s remind that fractional derivative Kaputo of the random inappropriate order
-known measurable vector function. We will understand a fractional derivative as left-side fractional derivative Kaputo [1] - [6] . Let’s remind that fractional derivative Kaputo of the random inappropriate order ![]() from function
from function![]() , is defined by expression
, is defined by expression
![]() (2)
(2)
Besides in space ![]() the terminal set M is allocated. The running-away player seeks to place the aim of the pursuing player to bring z to a set M, to it. The problem of prosecution about rapprochement of a trajectory of the conflict operated system (1) with a terminal set M for terminating time from the standard initial positions
the terminal set M is allocated. The running-away player seeks to place the aim of the pursuing player to bring z to a set M, to it. The problem of prosecution about rapprochement of a trajectory of the conflict operated system (1) with a terminal set M for terminating time from the standard initial positions ![]() is considered. Let’s say that differential game (1) can be finished from initial situation
is considered. Let’s say that differential game (1) can be finished from initial situation ![]() during
during ![]() if there is such measurable function
if there is such measurable function ![]() that the solution of the equation
that the solution of the equation
![]()
belongs to a set M at the time of ![]() at any measurable functions
at any measurable functions ![]()
![]() .
.
This work is dedicated to the receipt of sufficient conditions for the completion of the prosecution managed fractional order systems adjacent to the study [12] - [22] . Some results of this paper were announced at the International Labour Conference [16] [17] . In such a setting the pursuit problem was studied in [8] - [11] , but it was devoted to the study of control systems of the whole order. In this sense, this paper summarizes these works.
3. Results and Discussion
Let’s pass to the formulation of the main results. Everywhere further: 1) the terminal set M has an appearance![]() , where the
, where the![]() ―linear subspace
―linear subspace![]() ,
,![]() ―subset of a subspace of L―orthogonal addition
―subset of a subspace of L―orthogonal addition![]() ; 2)
; 2)![]() ―operator of orthogonal projection from
―operator of orthogonal projection from ![]() on L; 3) operation
on L; 3) operation ![]() is understood as operation of a geometrical subtraction [8] .
is understood as operation of a geometrical subtraction [8] .
Let ![]() -matrix
-matrix![]() ―an exponential curve [1] and
―an exponential curve [1] and ![]()
![]()
![]()
![]() ;
;
![]() (3)
(3)
Theorem 1. If in game (1) at some![]() , inclusion is carried out
, inclusion is carried out
![]() (4)
(4)
That from initial situation ![]() is possible will finish prosecution during
is possible will finish prosecution during![]() .
.
Let now the ![]() -arbitraries splitting a piece
-arbitraries splitting a piece![]() ,
, ![]() и
и![]() ,
,
![]() (5)
(5)
Theorem 2. If in game (1) at some![]() , inclusion is carried out
, inclusion is carried out
![]() (6)
(6)
That from initial situation ![]() is possible will finish prosecution during
is possible will finish prosecution during![]() .
.
Let’s designate through ![]() set
set ![]() defined at all
defined at all![]() . Let’s consider
. Let’s consider
integral
![]() (7)
(7)
Theorem 3. If in game (1) at some![]() , inclusion is carried out
, inclusion is carried out
![]() (8)
(8)
that from initial situation ![]() is possible will finish prosecution during
is possible will finish prosecution during![]() .
.
Proof of the theorem 1. Two cases are possible: 1)![]() ;
;![]() . Case 1) trivial as at
. Case 1) trivial as at ![]() of inclusion (4) we have
of inclusion (4) we have ![]() or
or ![]() that is equivalent to inclusion
that is equivalent to inclusion![]() . Let now
. Let now![]() . After a
. After a
theorem condition![]() , then there will be vectors
, then there will be vectors ![]() and
and
![]() such that (see (3), (4))
such that (see (3), (4))![]() . Further, according to determination of integral
. Further, according to determination of integral ![]() there is a summable function
there is a summable function ![]() that
that![]() .
.
Considering this equality, we will consider the equation
![]() (9)
(9)
Relatively ![]() at fixed
at fixed ![]() and
and![]() . As
. As![]() , the equation (9) has the decision. We will choose the least in lexicographic sense from all solutions of the equation (9) and we will designate it through
, the equation (9) has the decision. We will choose the least in lexicographic sense from all solutions of the equation (9) and we will designate it through![]() . Function
. Function![]() , is lebegovsk measurable on
, is lebegovsk measurable on ![]() and borelevsk measurable on
and borelevsk measurable on ![]() [7] . Therefore for any measurable function
[7] . Therefore for any measurable function![]() , function
, function![]() , will be lebegovsk measurable function [7] . Let’s put
, will be lebegovsk measurable function [7] . Let’s put ![]() and we will show that at such way of management of the parameter of u the trajectory
and we will show that at such way of management of the parameter of u the trajectory ![]() gets on a set M in time, not surpassing
gets on a set M in time, not surpassing![]() .
.
Really, on (9) for the decision![]() , the equation
, the equation
![]()
we have ( [1] , p. 414)
![]()
As![]() . Further we have
. Further we have![]() . From here we will receive that
. From here we will receive that![]() . The theorem is proved completely.
. The theorem is proved completely.
Proof of the theorem 2. In view of a case triviality we will begin ![]() consideration with a case
consideration with a case![]() .
.
We have (see (5), (6))![]() .
. ![]() is alternating integral with an
is alternating integral with an
initial set ![]() [8] . Therefore for it semigroup property [4] is executed
[8] . Therefore for it semigroup property [4] is executed
![]() (10)
(10)
where the![]() ―arbitraries positive fixed number
―arbitraries positive fixed number![]() ;
;![]() ,the
,the![]() ―arbitraries measurable function with values from Q.
―arbitraries measurable function with values from Q.
Let![]() ―arbitrary measurable function
―arbitrary measurable function![]() . According to theorem conditions in an instant
. According to theorem conditions in an instant ![]() is known a narrowing
is known a narrowing![]() , functions
, functions ![]() on a piece
on a piece![]() . Follows from inclusion (10) that for the arbitrary function
. Follows from inclusion (10) that for the arbitrary function![]() , we have
, we have
![]() (11)
(11)
Thus, for the arbitrary function![]() , inclusion takes place (12). Therefore, at
, inclusion takes place (12). Therefore, at ![]() , inclusion is fair (12). From here existence of measurable function
, inclusion is fair (12). From here existence of measurable function![]() , such follows that
, such follows that ![]() and
and
![]() (12)
(12)
Then
![]() (13)
(13)
Further we argue similarly. As
![]() (14)
(14)
Let’s receive
![]() (15)
(15)
For the arbitrary measurable function![]() . Therefore, there is a measurable function
. Therefore, there is a measurable function![]() , such that
, such that ![]() and
and
![]() (16)
(16)
Follows from a ratio (16) that
![]() (17)
(17)
etc. It is clear, that there is a natural number j it that: 1)![]() ; 2) on the known function
; 2) on the known function![]() , where the
, where the ![]() narrowing of function
narrowing of function![]() , on a piece
, on a piece![]() , will be the measurable function
, will be the measurable function ![]()
![]() meeting a condition ((17))
meeting a condition ((17))
![]() (18)
(18)
But
![]() (19)
(19)
Therefore ((18), (19))
![]() (20)
(20)
Similarly on formulas (18), (19), (20) finally we receive
![]()
Thus, for any point ![]() we have
we have![]() , that is the trajectory, left a point
, that is the trajectory, left a point![]() , in an instant
, in an instant ![]() turns out M on a set. The theorem is proved completely.
turns out M on a set. The theorem is proved completely.
Proof of the theorem 3. Owing to a condition of the theorem (8) we have ![]() . Therefore (7), there is such measurable function
. Therefore (7), there is such measurable function ![]() , that
, that
![]() (21)
(21)
Let ![]() arbitrary measurable function, by definition of subtraction operation
arbitrary measurable function, by definition of subtraction operation ![]() we will receive
we will receive
![]() (22)
(22)
From here owing to a condition of measurability existence of the measurable functions ![]() defined on a piece
defined on a piece ![]() follows and
follows and
![]() (23)
(23)
We will determine function by the found measurable function ![]()
![]() (24)
(24)
For the decision ![]() corresponding to functions
corresponding to functions ![]() we have (21)-(24)
we have (21)-(24)
![]()
From here![]() , that is the trajectory which left a point
, that is the trajectory which left a point ![]() in an instant
in an instant ![]() turns out M on a set. The theorem is proved completely.
turns out M on a set. The theorem is proved completely.
4. Conclusion
Summarizing the results, we conclude that the differential game of pursuit of fractional order (1), starting from the position can be completed in time, respectively. Thus, to solve the game problem kind of persecution (1), we used a derivative of fractional order Caputo, which is determined by the expression (2). Many (3) analogue of the so-called first integral Pontryagin, including (4) gives the first sufficient condition for the possibility of the persecution of the task. Many (5)―an analog of the second integral Pontryagin, inclusion (6) gives the second sufficient condition for the possibility of the persecution of the task. Lots (7)―analogue N. Satimova third method, and the inclusion (8) gives a sufficient condition for the third opportunity to end the game. In Theorems 1 - 3, we obtain sufficient conditions for the solution of relevant problems in this form.