Probabilistic Model of Technical Queuing Systems with Subsystems for Detection and Recovery of Failures ()
Received 10 December 2015; accepted 2 August 2016; published 5 August 2016

1. Introduction
Reliability is a technical system property to preserve its characteristics under the given maintenance conditions. Taking into account the above definition, the development and distribution of complex systems, such as computer systems, communication systems, automatic control systems, etc. require new approaches in order to raise their reliability characteristics. Creation of new technical systems requires high quality and reliability standards, which in its turn, makes it necessary to develop appropriate methods of calculation and forecast of new technology reliability. Due to various reasons (complexity, cumbersome, inaccessibility, etc.), we have to study not the system itself, but a formal description of its peculiarities, which are essential for the assessment of its reliability. Hence in order to calculate system reliability characteristics it is necessary to create a mathematical model of system operation and to develop computer methods, algorithms and reliability analysis programs. The influence of the types of distribution laws of characteristics of elements on system reliability, taking into consideration system operation peculiarities, such as element condition control, aftereffects of failures, the necessity of taking into account non-simultaneity of element operation, switching to the reserve, opportunity of system reconfiguration in the process of system operation, introduction of different reservation types, etc. lead to a necessity of system analysis with arbitrary distribution laws. At present, however, not only practical methods are absent, but theoretical calculation methods of effective operation of systems of variable structures, which can change randomly over short time intervals, are absent as well. Structural changes are always related to the changes of functions performed by the system. The existing methods are unable to calculate reliability of current systems with a large number of states and complex relationships. A similar picture can be observed with the dynamically changing boundary between failures and operation states. Reliability theory problems of such complexity have not been sufficiently studied.
At present numerous publications are known which reflect technologies, logical, physical and program structure of contemporary computer networks [1] - [4] . Theoretical methods of analysis and synthesis of computer networks found a reflection in numerous articles and separate sections of monographs [5] - [11] oriented mainly on mathematicians. Complexity and multitude of approaches, absence of systematization of basic directions of analysis and synthesis of the computer networks create considerable difficulties for plan developers and designers willing to use theoretical approaches for solution to practical tasks.
2. Purpose
The article is dedicated to the development of one specific but a more generalized model of analysis and synthesis of complex networks that is based on the theory of systems and networks of mass service (theory of queues). The preculiatity of this model is in the use of methods of the theory of reliability for accounting of the reliable characteristics of serving devices. The article represents a certain perfection and generalization of previous works of the author [12] - [14] .
The given paper deals with the development of an analytical model of complex technical queuing systems with various operation states, taking into account servicer reliability and available time redundancy. It is also assumed that time reservation is used for system switching and reconfiguration, recovery after failures, for a repeated fulfillment of the performed task, etc.
The results of the presented work applied to reliability and efficiency analysis of the above-mentioned technical systems enable one to take into consideration the following peculiarities: variable system structure, a large number of states, arbitrary distribution laws of random factors, forms and types of failures and their aftereffects, ways and characteristics of element operability control system, operation peculiarities in real time, time of reconfiguration, availability of technical maintenance, breaks in the process of element operation, different states of hardware reserve; it also takes into account time reserve, multifunctionality of the system, choice of optimal parameters of the system.
The apparatus used in the paper includes classical methods of reliability theory, theory of mathematical and functional analysis, probability theory, theory of differential equations, theory of integral equations, theory of graphs and queuing theory.
The results of the paper can be applied to system operation reliability and efficiency assessment both at the stage of system design and at operation stage in order to ensure optimal characteristics.
The present paper develops a technical queuing system operation model under the following assumptions:
・ The number of servicers is n;
・ The system performs a task, for the accomplishment of which under trouble-free conditions of all n servicers, time t is required;
・ The servicers are affected by the Poisson flow of gradual and sudden failures, the total intensity of which in a general case depends on the number of servicers and is equal to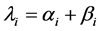 , where
, where  is the intensity of the gradual failure flow, and
is the intensity of the gradual failure flow, and 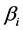 is the intensity of sudden failures;
is the intensity of sudden failures;
・ The system is designed to ensure availability of a reliable control, which with a time distribution function 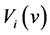 confirms the fact of gradual or sudden failures with a subsequent recovery of the failed servicers;
confirms the fact of gradual or sudden failures with a subsequent recovery of the failed servicers;
・ As soon as they are detected, the failed servicers are sent for recovery, which is performed with an arbitrary distribution function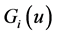 ;
;
・ It is assumed in the given model that the failures do not depreciate the work that has been already done and after the recovery of a servicer the task is resumed at the failure point.
3. Introduction of Special Functions
For a probabilistic description of the mentioned system the following functions are introduced:
・ 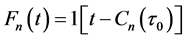 is a unit function of task accomplishment time distribution according to which the task is accomplished in a minimum required time
is a unit function of task accomplishment time distribution according to which the task is accomplished in a minimum required time 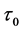 when the technical system is serviceable (the number of trouble-free servicers is
when the technical system is serviceable (the number of trouble-free servicers is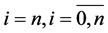 );
);
・  is a time distribution function of non-accomplishment of the task in time t;
is a time distribution function of non-accomplishment of the task in time t;
・  is a probability distribution function of task accomplishment in the system with i operable servicers in a time less than t, under the condition that a part of the task
is a probability distribution function of task accomplishment in the system with i operable servicers in a time less than t, under the condition that a part of the task  has already been accomplished at time
has already been accomplished at time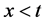 , by a system with
, by a system with 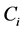 productivity.
productivity.
Using the introduced functions, on the basis of probabilistic considerations we can write the following integral equation defining the process of task fulfillment in the described system:
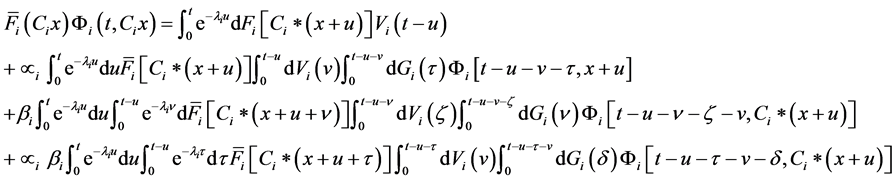 (1)
(1)
We will explain the meaning of the expressions involved in Equation (1):
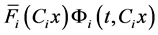 is the shared probability of the following events:
is the shared probability of the following events:
1) ![]() is the probability of an event for which at time
is the probability of an event for which at time ![]() the
the ![]() -th part of the task arriving at time
-th part of the task arriving at time ![]() will be done by the system in the state with i operable servicers, the whole task, however, will not be accomplished;
will be done by the system in the state with i operable servicers, the whole task, however, will not be accomplished;
2) ![]() is the probability of an event for which the incoming task to be served will be accomplished during the time less than t by the system in a state with i operable servicers, under the condition that during time
is the probability of an event for which the incoming task to be served will be accomplished during the time less than t by the system in a state with i operable servicers, under the condition that during time ![]() the
the ![]() -th part of the task has been accomplished;
-th part of the task has been accomplished;
![]() is the probability of the following shared events:
is the probability of the following shared events:
1)![]() ―at time u in the interval
―at time u in the interval ![]() no possible types of failures will occur (gradual; sudden);
no possible types of failures will occur (gradual; sudden);
2)![]() ―at time
―at time ![]() the task will be accomplished by the system in a state with i operable servicers;
the task will be accomplished by the system in a state with i operable servicers;
3)![]() ―at time
―at time ![]() the reliable control confirming trouble-free accomplishment of the task ends.
the reliable control confirming trouble-free accomplishment of the task ends.
![]() ―is the probability of the following shared events:
―is the probability of the following shared events:
1)![]() ―at time u in the interval
―at time u in the interval ![]() a gradual failure occurred, which was immediately detected by the monitoring system;
a gradual failure occurred, which was immediately detected by the monitoring system;
2)![]() ―at time
―at time ![]() of the interval
of the interval ![]() the task was not accomplished by the system in the state with i operable facilities;
the task was not accomplished by the system in the state with i operable facilities;
3)![]() ―at time v in the interval
―at time v in the interval ![]() the system of reliable control will accomplish its work, which will confirm the fact of an occurred failure, resulting in sending the system for recovery;
the system of reliable control will accomplish its work, which will confirm the fact of an occurred failure, resulting in sending the system for recovery;
4)![]() ―at time
―at time ![]() in the time interval
in the time interval ![]() the system will be recovered after a failure;
the system will be recovered after a failure;
5)![]() ―is the probability that during a period of time less than
―is the probability that during a period of time less than ![]() the system will accomplish the task under the condition that its
the system will accomplish the task under the condition that its ![]() -th part has been already done over time
-th part has been already done over time ![]() by the system in a state with i operable devices;
by the system in a state with i operable devices;
![]() is the probability of the following shared events:
is the probability of the following shared events:
1)![]() ―at time u in the interval
―at time u in the interval ![]() a sudden failure occurred, which was immediately detected by the control system;
a sudden failure occurred, which was immediately detected by the control system;
2)![]() ―over time
―over time ![]() in the interval
in the interval ![]() the task was not accomplished by the system in a state with i operable servicers;
the task was not accomplished by the system in a state with i operable servicers;
3)![]() ―over time v in the interval
―over time v in the interval ![]() the system of reliable control will accomplish its work, which will confirm the fact of the occurred failure that resulted in sending the system for recovery;
the system of reliable control will accomplish its work, which will confirm the fact of the occurred failure that resulted in sending the system for recovery;
4)![]() ―at time in the interval
―at time in the interval ![]() the system will be recovered after a failure;
the system will be recovered after a failure;
5)![]() ―is the probability that over the time less than
―is the probability that over the time less than ![]() the system will accomplish the task under the condition that its
the system will accomplish the task under the condition that its ![]() -th part has already been done during time
-th part has already been done during time ![]() by the system in a state with i operable servicers;
by the system in a state with i operable servicers;
![]() ―is the probability of the following shared events:
―is the probability of the following shared events:
1) ![]() is the probability of an event during which at time u in the interval
is the probability of an event during which at time u in the interval ![]() a sudden failure will occur;
a sudden failure will occur;
2) ![]() is the probability of an event when at time
is the probability of an event when at time ![]() in the time interval
in the time interval ![]() a gradual failure will occur;
a gradual failure will occur;
3) ![]() is the probability that over time
is the probability that over time ![]() the
the ![]() -th part of the task will be done, but it will not be accomplished by the system in a state with i operable servicers;
-th part of the task will be done, but it will not be accomplished by the system in a state with i operable servicers;
4)![]() ―over time v in the interval
―over time v in the interval ![]() the system of reliable control will accomplish its work confirming the fact of a sudden failure that resulted in sending the system for recovery;
the system of reliable control will accomplish its work confirming the fact of a sudden failure that resulted in sending the system for recovery;
5)![]() ―at time
―at time ![]() in the time interval
in the time interval ![]() the system will be recovered after a sudden failure;
the system will be recovered after a sudden failure;
6)![]() ―is the probability that during the time less than
―is the probability that during the time less than ![]() the system will accomplish the task under the condition that the
the system will accomplish the task under the condition that the ![]() -th part of it has already been done over time
-th part of it has already been done over time ![]() by the system with i operable servicers:
by the system with i operable servicers:
![]() (2)
(2)
If we divide both parts Equation (2) into ![]() and differentiate it with respect to x, after simple transformations we have
and differentiate it with respect to x, after simple transformations we have
![]() (3)
(3)
The solution of the above equation can be expressed as:
![]() (4)
(4)
The constant С is defined by Equation (2), under the condition that![]() , in the following way:
, in the following way:
![]() . Substituting it in (4), we have:
. Substituting it in (4), we have:
![]() (5)
(5)
Using the obtained probabilities we can easily find various indicators of the effective functioning of the described system. In particular,
when no work has been done before the starting time, i.e. when![]() , we have:
, we have:
![]() (6)
(6)
when there are no undetectable failures, i.e. when![]() ,
, ![]() , Formula (6) takes the following form:
, Formula (6) takes the following form:
![]() (7)
(7)
Differentiating Equation (7) with respect to s when s tends to zero, we obtain the average time of task accomplishment under defined conditions:
![]() ;
;
where ![]() is the average control time,
is the average control time, ![]() is the average recovery time.
is the average recovery time.
When there are no detectable failures in the system, i.e. when ![]() and, consequently,
and, consequently, ![]() Formula (6) takes the following form:
Formula (6) takes the following form:
![]() (8)
(8)
Differentiating Equation (8) with respect to s when s tends to zero and opening the indeterminate according L’Hopital’s rules, we obtain the average time of task accomplishment under defined conditions:
![]() ;
;
For the general case when![]() ,
, ![]() ,
, ![]() similar transformations of Formula (5) give the average time of task accomplishment:
similar transformations of Formula (5) give the average time of task accomplishment:
![]() ;
;
The formula for calculating the availability ratio of the described type of the technical system will have the following form:
![]()
4. Conclusions
Results obtained in the given paper represent a certain generalization of the results already described in technical literature. They enable one to calculate probabilities of possible states of the system described above, the application of which makes it possible to express other important characteristics of a reliable and efficient operation of such systems.
The adequacy of the proposed model, taking into consideration the above-mentioned assumptions, can be proved by means of strict mathematical considerations and transformations as well as by the obtained conclusions.
The assertion that the model is new and the most generalized is proved by the fact that under certain assumptions with respect to system parameters, models are obtained that coincides with some models already known in literature.
The results of the article can be successfully applied to the analysis and synthesis of complex technical systems, such as computer data transmission systems, local and distributed, stationary and mobile computer and communication systems and networks, flexible production lines, various automatic control systems for manufacturing, organizational and technological processes as well as to other sophisticated technical systems serving both civil and military purposes. They can be used both for the assessment of the existing and the required levels of reliability, durability, productivity and operation efficiency of complex technical systems both at the design and operation stages.