About the Influence of the Giant Planets on Long-Term Evolution of Global Temperature ()


1. Formulation of the Problem
The observed variability of global temperature [1] is usually explained through the decrease in the coefficient of the grayness of the Earth caused by increased content of greenhouse gases in the atmosphere, such as CO2 [2], i.e. by the anthropogenic ally caused increase in the greenhouse effect. The validity of such views raises some doubts, as their validity is based either on the results of the climate simulation [3], or on the results of the regression analysis [4], in relation to which the fullness of the used set of regression does not seem certain. At the same time, just the results of climate modeling do not seem to be quite reliable, above all, for the reasons stated in [5]. Thus, the uniqueness of the solution of global circulation equation (the Navier-Stokes equations in a rotating coordinate system) is more than controversial in view of the phenomenon of turbulence, which entails a fundamental limitation on the applicability of numerical solution methods, and slew rate of errors inherent in the initial conditions, fundamentally limits reasonable time of prediction through the duration of the synoptic cycle value [5].
2. Working Hypothesis and Its Testing
Based on simple numerical estimates, one can easily obtain the mean displacement of the center of gravity of the solar system relative to the center of the Sun that is equal to 5/4 of its radius. The oppositions of two heaviest planets in the solar system (Jupiter and Saturn) repeated at a frequency of about half the frequency of revolution of Saturn around the Sun (1/29.46 years), as is easily seen, can cause this kind of bias by a value of about 1.64 of solar radii. This can, in turn, determine a significant asymmetry in the distribution of the photosphere, i.e. Sun’s radiation pattern, as well as change in the Earth-to-Sundistance by about 0.67%. Such variations are equivalent to a change in the solar constant value of about 20 W/m2, despite the fact that energy equivalent of the anthropogenically caused greenhouse effect is equal, according to the authors [2], to a value that is almost an order of magnitude smaller (~2.4 W/m2). Such changes are bound to lead to changes in the parameters of the oscillatory energy-balance system of the Earth, primarily due to the albedo oscillations caused by the total cloud amount. These fluctuations have to cause parametric resonance at the frequencies corresponding to the doubling of the period of oscillations caused by oppositions of Jupiter and Saturn. Based on these considerations, the following regression model was built for the global temperature:
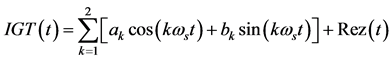 (1)
(1)
where: IGT is a global temperature deviation from the climatic norm;  years (Saturn’s
years (Saturn’s
orbital period around the Sun), Rez(t) is residual of the simulation.
The amount of (1) is limited by the superscript two due to the limitations of the full extent of seriesby 160 years. When preparing the data, it was revealed that the crutem3 [1] database did not completely rule out seasonal variations in global temperature, and its contribution with a full amplitude of 0.66 K (on) four harmonics of seasonal variation was also included in the model. As Figure 1 showed, the statistical significance of the model (1) was at the level of the Fisher statistical value being equal to 3503 and a coefficient of determination of 65%. Note that without a model (1), the trend of series was 0.52 ± 0.01 K/100 years (the coefficient of determination was 42%), with a statistical significance being at the level of the Fisher statistic equal to 1410, and after eliminating the effect of parametric resonance of opposition of giant planets (1), it was equal to 0.01 ± 0.008 K/100 years at a statistical significance being at the level of Fisher statistic equal to 0.4 minutes.
![]()
Figure 1. Model of global temperature variability.
![]()
Figure 2. Forecast of global temperature deviations from the climatic normals.
It is important to note that the residuals of the model (1) are a succession close to white noise: the Durbin- Watson statistic is 2.14 for it, and the coefficient of determination of the integrated periodogram of the straight line passing through the origin of coordinates is equal to 90%. Figure 2 shows the forecast for future changes in global temperature and its margin of error is 0.24 K.
3. Conclusions
The main contribution to long-term changes in global temperature is formed by the parametric resonance phenomenon along with the phenomenon of oppositions of Jupiter and Saturn giant planets. The contribution of such planets as Uranus and Neptune cannot be determined today using the regression modeling techniques due to the limited succession of observations and its small length of time in comparison with the periods of the parametric resonance of said planets (about 330 years).
Even more this limitation relates to the oppositions of the giant planets of a ratio being higher than 2, i.e. to the oppositions involving three or more giant planets.
Acknowledgements
This paper was partially supported by the RFBR grant No. 13-05-01036a.