Universe and Matter Conjectured as a 3-Dimensional Lattice with Topological Singularities ()
Received 30 June 2016; accepted 30 July 2016; published 2 August 2016

1. Introduction
This paper presents a theory recently developed [1] and published in a book [2] [3] , which shows that an Eulerian approach of the deformation of a Newtonian lattice in an absolute space can furnish an investigation frame extremely rich and interesting for physics, if judicious elastic and structural properties of the considered lattice are postulated. Indeed, it shows very strong and often perfect analogies with all the modern physics theories of the macrocosm and microcosm, as the Maxwell equations, the special relativity, the Newtonian gravitation, the general relativity, the modern cosmology, the quantum physics and the standard model of elementary particles.
This book does not present a theory of everything which would be completely elaborated and usable, but it would and could be extremely fruitful to give simple explanations to the modern physics theories which are very difficult, if not impossible, to deeply understand. It could also and above all be useful to define close links and unifying bridges between the diverse theories of modern physics.
In a first part, one summarizes autonomously a first book published in French during year 2013 [4] (also recently translated in English [5] ), which lays methodically the foundations of an original approach of the solid lattices deformation using the Euler coordinates, and which introduces in details the concept of tensor dislocation charges and tensor disclination charges within a lattice. This new concept allows one to quantify the topological singularities, which can appear at the microscopic scale of a solid lattice. On the basis of this original approach of the solid lattices and their topological singularities, one can deduce a set of fundamental and phenomenological equations allowing to treat rigorously the macroscopic spatiotemporal evolution of a Newtonian solid lattice which deforms in the absolute space of an external observer laboratory.
In a second part, one introduces an imaginary lattice, named “cosmic lattice”, with quite special elastic and structural properties. The Newton equation of this lattice and its topological singularities present then a set of very surprising properties, which will be progressively developed in the course of the chapters. It will appear strong and amazing analogies with all modern physics theories: Maxwell equations, special relativity, Newtonian gravitation, general relativity, modern cosmology, quantum physics and standard model of elementary particles.
2. The Problem of Unified Theories
One fundamental problem of modern physics is the search for a theory of everything able to explain the nature of space-time, what matter is and how matter interacts. Since the 19th century, physicists have attempted to develop unified field theories [6] , which would consist of a single coherent theoretical framework able to account for several fundamental forces of nature. For instance:
・ Grand Unified Theory [7] merges electromagnetic, weak and strong interaction forces,
・ Quantum Gravity [8] , Loop Quantum Gravity [9] and String Theories attempt to describe the quantum properties of gravity,
・ Super-symmetry [10] - [15] proposes an extension of the space-time symmetry relating the two classes of elementary particles, bosons and fermions,
・ String and Superstring Theories [16] - [23] are theoretical frameworks incorporating gravity in which point- like particles are replaced by one-dimensional strings, whose quantum states describe all types of observed elementary particles,
・ M-Theory [24] - [32] is a unifying theory of five different versions of string theories, with the surprising property that extra dimensions are required for its consistency.
However, none of them is able to consistently explain at the present and same time electromagnetism, relativity, gravitation, quantum physics and observed elementary particles. Many physicists believe now that 11-dimensional M-theory is the theory of everything. However, there is no widespread consensus on this issue and, at present, there is no candidate theory able to calculate the fine structure constant or the mass of the electron. Particle physicists expect that the outcome of the ongoing experiments-search for new particles at the large particle accelerators and search for dark matter-are needed to provide further input for a theory of everything.
In the recent theoretical work presented in the book [2] [3] , it is suggested that Universe could be a massive elastic 3D-lattice, and that fundamental building blocks of Ordinary Matter could consist of topological singularities of this lattice, namely diverse dislocation loops and disclination loops. We find, for an isotropic elastic lattice obeying Newton’s law, with specific assumptions on its elastic properties, that the behaviors of this lattice and of its topological defects display “all” known physics, unifying electromagnetism, relativity, gravitation and quantum physics, and resolving some longstanding questions of modern cosmology. Moreover, studying lattices with axial symmetries, represented by “colored” cubic 3D-lattices, one can identify a lattice structure whose topological defect loops coincide with the complex zoology of elementary particles, which could open a promising field of research.
In this paper, motivations, main steps and principal results of the new theories presented in the two parts of book [2] [3] are summarized as succinctly as possible, without showing the mathematical concepts and developments contained in the book.
3. Motivation of the First Part: Searching for a New Description of the Lattice Deformation
3.1. Eulerian Deformation Theory of Newtonian Lattices
When one desires to study the solid deformation, one generally uses Lagrangian coordinates to describe the evolution of the deformations, and diverse differential geometries to describe the topological defects contained in the solid.
The use of Lagrangian coordinates presents a number of inherent difficulties. From the mathematical point of view, the tensors describing the continuous solid deformation are always of order higher than one concerning the spatial derivatives of the displacement field components, which leads to a very complicated mathematical formalism when the solid presents strong distortions (deformations and rotations). To these mathematical difficulties are added physical difficulties when one has to introduce some known properties of solids. Indeed, the Lagrangian coordinates become practically unusable, for example when one has to describe the temporal evolution of the microscopic structure of a solid lattice (phase transitions) and of its structural defects (point defects, dislocations, disclinations, boundaries, etc.), or when it is necessary to introduce some physical properties of the medium (thermal, electrical, magnetic or chemical properties) leading to scalar, vectorial or tensorial fields in the real space.
The use of differential geometries in order to introduce topological defects as dislocations in a deformable continuous medium has been initiated by the work of Nye [33] (1953), who showed for the first time the link between the dislocation density tensor and the lattice curvature. On the other hand, Kondo [34] (1952) and Bilby [35] (1954) showed independently that the dislocations can be identified as a crystalline version of the Cartan’s concept [36] of torsion of a continuum. This approach was generalized in details by Kröner [37] (1960). However, the use of differential geometries in order to describe the deformable media leads very quickly to difficulties similar to those of the Lagrangian coordinates system. A first difficulty arises from the complexity of the mathematical formalism which is similar to the formalism of general relativity, what makes very difficult to handle and to interpret the obtained general field equations. A second difficulty arises with the differential geometries when one has to introduce topological defects other than dislocations. For example, Kröner [38] (1980) has proposed that the existence of extrinsic point defects could be considered as extra-matter and introduced in the same manner that matter in general relativity under the form of Einstein equations, which would lead to a pure Riemannian differential geometry in the absence of dislocations. He has also proposed that the intrinsic point defects (vacancies and interstitials) could be approached as a non-metric part of an affine connection. Finally, he has also envisaged introducing other topological defects, as disclinations for example, by using higher order geometries much more complex, as Finsler or Kawaguchi geometries. In fact, the introduction of differential geometries implies generally a heavy mathematical artillery (metric tensor and Christoffel symbols) in order to describe the spatiotemporal evolution in infinitesimal local referentials, as shown for example in the mathematical theory of dislocations of Zorawski [39] (1967).
In view of the complexity of calculations in the case of Lagrangian coordinates as well as in the case of differential geometries, it seemed that it would be better to develop a much simpler approach of deformable solids, but at least equally rigorous, which has been finally published in a first book [4] during year 2013: la théorie eulérienne des milieux déformables.
In the first part of book [2] [3] , one presents a summary of this new and original Eulerian approach of the deformation of solids through several sections:
The first section introduces the Eulerian deformation theory of Newtonian lattices. The deformation of a lattice is characterized by distortions and contortions. A vectorial representation of the tensors, presenting undeniable advantages over purely tensorial representation thanks the possibility to use the powerful formalism of the vectorial analysis, allows to obtain the geometro-compatibility equations of the lattice which insure its solidity, and the geometro-kinetics equations of the lattice, which allow one to describe the deformation kinetics. One introduces then the physics in this topological context, namely the Newtonian dynamics and the Eulerian thermo-kinetics (based on the first and second principles of thermodynamics). With all these ingredients, it becomes possible to describe the particular behaviors of a solid lattice, as the elasticity, the anelasticity, the plasticity and the self-diffusion. This first section ends with the establishment of the complete set of evolution equations of a lattice in the Euler coordinate system.
The second section is dedicated to the applications of the Eulerian theory. It presents very succinctly some examples of phenomenologies of everyday solids. One shows how to obtain the functions and equations of state of an isotropic solid, what are the elastic and thermal properties which can appear, how waves propagate and why there exist thermoelastic relaxations, what are the mass transport phenomena and why it could appear inertial relaxations, what are the common phenomenologies of anelasticity and plasticity, and finally how it can appear structural transitions of first and second order in a solid lattice.
3.2. Dislocation and Disclination Charges in Eulerian Lattices
Regarding the description of defects (topological singularities) which can appear within a solid, as dislocations and disclinations, it is a domain of physics initiated principally by the idea of macroscopic defects of Volterra [40] (1907). This domain experienced a fulgurant development during the twentieth century, as well illustrated by Hirth [41] (1985). The lattice dislocation theory started up in 1934, when Orowan [42] , Polanyi [43] and Taylor [44] published independently papers describing the edge dislocation. In 1939, Burgers [45] described the screw and mixed dislocations. And finally in 1956, Hirsch, Horne et Whelan [46] and Bollmann [47] observed independently dislocations in metals by using electronic microscopes. Concerning the disclinations, it is in 1904 that Lehmann [48] observed them in molecular crystals, and in 1922 that Friedel [49] gave them a physical explanation. From the second part of the century, the physics of lattice defects has grown considerably.
In the first part of the books [2] [3] , the dislocations and the disclinations are approached by introducing intuitively the concept of dislocation charges by using the famous Volterra pipes [40] (1907) and an analogy with the electrical charges. With Euler coordinates, the concept of dislocation charge density appears then in an equation of geometro-compatibility of the solid, when the concept of flux of charges is introduced in an equation of geometro-kinetics of the solid.
The rigorous formulation of the charge concept in the solids makes the essential originality of this approach of the topological singularities. The detailed development of this concept leads to the appearance of tensorial charges of first order, the dislocation charges, associated with the plastic distortions of the solid (plastic deformations and rotations), and of tensorial charges of second order, the disclination charges, associated with the plastic contortions of the solid (plastic flexions and torsions). It appears that these topological singularities are quantified in a solid lattice and that they have to appear as strings (thin tubes) which can be modelized as unidimensional lines of dislocation or disclination, or as membranes (thin sheets) which can be modelized as two-dimensional boundaries of flexion, torsion or accommodation.
The concept of dislocation and disclination charges allows one to find rigorously the main results obtained by the classical dislocation theory. But it allows above all to define a tensor 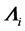 of linear dislocation charge, from which one deduces a scalar
of linear dislocation charge, from which one deduces a scalar 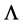 of linear rotation charge, which is associated with the screw part of the dislocation, and a vector
of linear rotation charge, which is associated with the screw part of the dislocation, and a vector 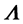 of linear flexion charge, which is associated with the edge part of the dislocation. For a given dislocation, both charges
of linear flexion charge, which is associated with the edge part of the dislocation. For a given dislocation, both charges  and
and 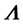 are perfectly defined without needing a convention at the contrary of the classical definition of a dislocation with its Burger vector! On the other hand, the description of the dislocations in the Eulerian coordinate system by the concept of dislocation charges allows one to treat exactly the evolution of the charges and the deformations during very strong volumetric contractions and expansions of a solid medium.
are perfectly defined without needing a convention at the contrary of the classical definition of a dislocation with its Burger vector! On the other hand, the description of the dislocations in the Eulerian coordinate system by the concept of dislocation charges allows one to treat exactly the evolution of the charges and the deformations during very strong volumetric contractions and expansions of a solid medium.
The description of this new approach of the topological defects of a lattice is presented in the two following sections of part one of the book:
The third section is dedicated to the introduction of dislocation charges and disclination charges in the Eulerian lattices. After the analytical introduction of the concepts of density and flux of dislocation and disclination charges in the lattices, one presents a detailed review of the lattice macroscopic and microscopic topological singularities, which can be associated to the dislocation and disclination charges. Then one discusses the motion of dislocation charges within the lattice by introducing the dislocation charges flux and the Orowan relations. Finally, one deduces the Peach and Koehler force, which acts on the dislocations, and one establishes the new set of evolution equations of a lattice in the Euler coordinate system, which takes into account the existence of topological singularities within the lattice.
The fourth section is dedicated to the applications of the charge concept within the Eulerian solid lattice. It shows the elements of the dislocation theory in the everyday solids. One begins to show that, in the particular case of the deformation of isotropic lattices by pure shears, one can replace the shear strain tensor by the rotation vector, which allows one to find a set of equations, which corresponds strictly to all the Maxwell equations of electromagnetism! Then one shows how to calculate the fields and energies of the screw and edge dislocations in an isotropic lattice, just as the interactions, which can occur between dislocations. One finishes this section of applications by presenting the string model of dislocations, which is the fundamental model allowing one to explain most of the macroscopic behaviors of anelasticity and plasticity of crystalline solids.
4. Motivation of the Second Part: Searching for a “Cosmic Lattice”
In the first part of the book, it is shown that it is possible to calculate the resting energy  of the dislocations, which corresponds to the elastic energy stored in the lattice by their presence, and their kinetic energy
of the dislocations, which corresponds to the elastic energy stored in the lattice by their presence, and their kinetic energy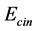 , which corresponds to the kinetic energy of the lattice particles mobilized by their movement. This allows to assign to the dislocations a virtual inertial mass
, which corresponds to the kinetic energy of the lattice particles mobilized by their movement. This allows to assign to the dislocations a virtual inertial mass  which satisfies relations similar to the famous equation
which satisfies relations similar to the famous equation 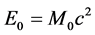 of the Einstein special relativity, but which is obtained here through purely classical calculations, without using relativity principles! Moreover, at high velocity, the dislocation dynamics satisfy also the special relativity principles and the Lorentz transformations.
of the Einstein special relativity, but which is obtained here through purely classical calculations, without using relativity principles! Moreover, at high velocity, the dislocation dynamics satisfy also the special relativity principles and the Lorentz transformations.
It is also shown in the first part that it appears, in the case of isotropic solid media presenting a constant and homogeneous volumetric expansion, a perfect and complete analogy with the Maxwell equations of electromagnetism when the shear stress tensor is replaced by the rotation vector. The existence of an analogy between the electromagnetism and the theory of incompressible continuous media has already been distinguished very long ago by several authors, as shown by Whittaker [50] (1951). However, this analogy is much more complete in the first book [4] , because it is not restricted to one of the two Maxwell equation couples in the vacuum, but it is generalized to the two equation couples as well as to the diverse phenomenologies of dielectric polarization and magnetization of matter, just as to the electrical charges and the electrical currents! The analogy with the Maxwell equations is very surprising on account of the fact that it is initially postulated a solid lattice satisfying a simple and purely Newtonian dynamics in the absolute reference frame of the external observer laboratory, which is equipped with absolute orthonormal measuring rods and an absolute clock. At the contrary, the topological singularities within the lattice (dislocations and disclinations) with their respective charges, responsible for the plastic distortions and contortions of the lattice, are submitted to a relativistic dynamics within the lattice, due to the Maxwellian equation set governing the shear strains of the massive elastic lattice. From this point of view, the relativistic dynamics of the topological singularities is a direct consequence of the purely classical Newtonian dynamics of the elastic lattice in the absolute frame of the external observer!
Finally, it also appears in the first part that the tensorial aspect of the distortion fields at short distances of a localized topological singularities cluster formed by one or more dislocation or disclination loops can be easily neglected at great distances of the cluster, because the distortion fields can then be completely described by only two vectorial fields, the vectorial field of rotation by torsion and the vectorial field of curvature by flexion, associated respectively to the only two scalar charges of the cluster, its scalar rotation charge and its scalar curvature charge. The rotation charge becomes the perfect analogue of the electrical charge in the Maxwell equations, when the curvature charge presents some analogy with the gravitational mass in the gravitation theory.
The existence of analogies between the theories of continuum mechanics and solid defects and the theories of electromagnetism, special relativity and gravitation has already been the subject of several publications, from which the more famous are most certainly those of Kröner [37] [38] . Excellent reviews in this physics field have also been published, in particular by Whittaker [50] (1951) and Unzicker [51] (2000). But none of these publications has gone as far as the approach published in the first book [4] concerning these highlighted analogies.
The numerous analogies which appear in the first part between the Eulerian theory of deformable media and the theories of electromagnetism, gravitation, special relativity, general relativity and even standard model of elementary particles, reinforced by the absence of particles analogue to magnetic monopoles, by a possible solution of the famous paradox of electron field energy and by the existence of a small asymmetry between curvature charges of vacancy or interstitial type, were sufficiently surprising and remarkable to alert any open and curious scientific spirit! But it was also clear that these analogies were, by far, not perfect. It was then tantalizing to analyze much more carefully these analogies and to try to find how to perfect them. That is the reason of the second part of the book, which is entirely allotted to the deepening, the improvement and the understanding of these analogies.
The second part of book [2] [3] is composed of five sections. Progressively, by introducing several judicious conjectures, one addresses the problem of the analogies existing between 1) the Eulerian theory of lattice deformation described in the first part, and applied to a very particular lattice, the cosmic lattice, and 2) the modern physics theories of the macrocosm and the microcosm, as the Maxwell equations, the special relativity, the Newtonian gravitation, the general relativity, the modern cosmology, the quantum mechanics and the standard model of elementary particles.
4.1. The “Cosmic Lattice” and Its Newton’s Equation
The first section of part two is dedicated to the introduction of the “cosmic lattice”. By introducing an imaginary lattice with very original elastic properties concerning the volumetric expansion, the shear strain and especially the rotation field, and by expressing the distortion free energy per volume unit of this lattice, one obtains a lattice, which presents a very particular Newton equation. Indeed, it appears in particular a novel force term directly related to the distortion free energy due to the singularities contained in the lattice, which will play subsequently a very important role for the analogies with the gravitation and the quantum physics.
Then one shows that the propagation of waves in this cosmic lattice presents interesting particularities: propagation of linearly polarized transversal waves is always associated with longitudinal wavelets, and propagation of pure transversal waves can only be obtained with circularly polarized waves (which will be strongly linked with the photons). On the other hand, when the local value of the lattice volumetric expansion becomes less than a given critical value, propagation of longitudinal waves disappears for the benefit of the appearance of localized longitudinal vibrations modes (which will be strongly linked with the quantum physics).
Afterwards, the calculation of the curvature of wave rays in the vicinity of a singularity of the lattice volumetric expansion allows one to find the conditions for which this expansion singularity becomes a real capturing trap for the waves, in other words a “black hole”!
Finally, one shows that such a cosmic lattice, if finite in the absolute space, can present dynamical volumetric expansion and/or contraction if it contains some quantity of expansion kinetics energy. This phenomenon is perfectly similar to the cosmological expansion of the universe! Following the signs and the values of the lattice elastic modules, several cosmological behaviors of the lattice can appear, some of which presenting phenomena as big-bang, rapid inflation and acceleration of the expansion velocity, which can be sometimes followed by a re-contraction of the lattice driving to a big-bounce phenomenon! One deduces that it is the expansion elastic energy contained in the lattice which is responsible for these phenomena, and notably for an expansion velocity increase, a phenomenon which has been recently discovered by the astrophysicists in the case of the present universe, and which has been attributed to a hypothetical “black energy”.
4.2. Maxwell’s Equations and Special Relativity
The second section is dedicated to the Maxwell equations and the special relativity. One begins to show that the Newton equation of the cosmic lattice can be separated in a curl part and a divergent part, and that the curl part creates a set of equations for the macroscopic rotation field, which is perfectly identical to the set of the Maxwell equations of the electromagnetism.
Then one shows that the Newton equation can also be separated in a different manner, in two partial Newton equations allowing to calculate on the one hand the distortion elastic fields associated with the topological singularities, and on the other hand the volumetric expansion perturbations associated with the distortion elastic energies of the topological singularities. By using the first partial Newton equation, on can calculate the fields and energies of elastic distortions generated by topological singularities within the cosmic lattice. One can then find conditions on the elastic modules of this lattice such as it is possible to attribute in a perfectly conventional manner an inertial mass to the topological singularities, which always satisfies the famous Einstein relation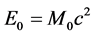 .
.
Then one demonstrates that the topological singularities satisfy a typically relativist dynamics when their velocity inside the lattice becomes close to the celerity of the transversal waves.
On these foundations, one finishes this section by discussing the analogy between this theory and the theory of special relativity. One notices that the cosmic lattice acts in fact as an aether, in which the topological singularities satisfy exactly the same properties than those of the special relativity concerning the length contraction, the time dilatation, the Michelson-Morley experiment and the Doppler-Fizeau effect. The existence of the cosmic lattice allows then to explain very simply some obscure sides of the special relativity, as for example the twin paradox!
4.3. Gravitation, General Relativity, Weak Interaction and Cosmology
The third section is dedicated to the gravitation and the cosmology. Thanks to the second partial Newton equation, one begins with the calculation of the external expansion perturbations, that is to say the external scalar gravitation field, associated with a localized macroscopic topological singularity, knowing either its distortion elastic energy, or its curvature charge, or its rotation charge.
Immediately afterwards, one describes also macroscopic vacancy singularities and macroscopic interstitial singularities, which can appear within the lattice in the form of a macroscopic hole in the lattice or an interstitial embedment of a piece of lattice. These singularities will become subsequently the ideal candidates to explain respectively the black holes and the pulsars of our universe.
By applying the calculations of the external gravitation field of topological singularities to localized microscopic topological singularities, in the form of loops of screw disclination, loops of edge dislocation or loops of mixed dislocation, one deduces the whole of the properties of these loops. It appears then the new concept of “curvature mass” of the edge dislocation loops, which corresponds to the equivalent mass associated to the gravitational effects of the curvature charges of these loops, and which can be positive (in the case of loops of vacancy type) or negative (in the case of loops of interstitial type). In fact, the curvature charge and the equivalent curvature mass which is associated do not appear in any other physics theory, neither in general relativity, nor in quantum physics, nor in standard model of elementary particles. The appearance of this new curvature charge is certainly the most important finding of our theory, because it is precisely that curvature mass which is responsible for a small asymmetry between the particles (hypothetically containing edge dislocation loops of interstitial type) and the antiparticles (hypothetically containing edge dislocation loops of vacancy type), which will play a fundamental role concerning the weak interaction and the cosmological evolution of the topological singularities within the universe!
By considering the gravitational interactions existing between the topological singularities composed essentially of screw disclination loops, one can deduce the behaviors of the measuring rods and clocks of local observers as a function of the local expansion field, which takes place within the cosmic lattice. One shows that, for any local observer, and whatever is the value of the local volumetric expansion of the lattice, the Maxwell equations remain always perfectly invariant, so that, for this local observer, the transversal wave velocity is a perfect constant, when the transversal wave velocity measured by a hypothetical observer situated outside the lattice in the absolute space depends strongly on the local expansion of the lattice!
One shows that these gravitational interactions present strong analogies with the Newton’s gravitation and with the general relativity, and one discusses in details the perfectly analogue points, as the perfect analogy with the Schwarzschild metric at great distances from massive objects and the curvature of wave rays by massive objects.
But one shows that this Eulerian theory of the cosmic lattice provides also new elements to the gravitation theory, notably modifications of the Schwarzschild metric at very short distances from massive objects, and a better understanding of the critical radii associated with black holes: the radii of the photon perturbation sphere and of the point of no return become both equal to the Schwarzschild radius , and the limit radius for which the time dilatation of a falling observer would stretch to an infinite value becomes zero, so that our theory is not limited beyond the Schwarzschild sphere for the description of a black hole.
, and the limit radius for which the time dilatation of a falling observer would stretch to an infinite value becomes zero, so that our theory is not limited beyond the Schwarzschild sphere for the description of a black hole.
One establishes next a complete table of all the gravitational interactions existing between the diverse topological singularities of the cosmic lattice, and one finds that the gravitational interactions between screw disclination loops is largely dominant.
By considering now a topological singularity formed by coupling a screw disclination loop with an edge dislocation loop, called a dispiration loop, it appears an interaction force between the rotation field of the screw loop and the curvature field of the edge loop, which is perfectly similar to a catch potential with a very small range, and which presents an interaction between the two loops perfectly analog to the weak interaction between elementary particles of the standard model.
On the basis of the cosmological behaviors of a lattice described in the first section, and the gravitational interactions between topological singularities described in the third section, on can imagine a very plausible scenario for the cosmological evolution of the topological singularities contained in a cosmic lattice, leading to the present structure of our universe. This scenario allows one to give a very simple explanation of several facts occurring during the universe expansion and still poorly understood, as the formation of galaxies, the disappearance of antimatter, the formation of gigantic black holes at the heart of the galaxies, and even the famous “dark matter” that the astrophysicists had to concoct for explaining the gravitational behavior of the galaxies.
In our theory, the dark matter would be in fact a sea of repulsive neutrinos in which the galaxies would have precipitated and would be immersed. Indeed, in the case of the simplest edge dislocation loops, analogically similar to neutrinos, the “gravitational curvature mass” dominates the inertial mass, so that the neutrinos should be the only particles gravitationally repulsive, when the antineutrinos should be gravitationally attractive. It is this surprising peculiarity which could explain the formation of a repulsive neutrinos sea playing the role of dark matter for the galaxies, due to the compression force exerted by the repulsive neutrinos sea on the galaxies periphery!
Finally, one shows how can be treated the Hubble constant, the galaxy redshift and the evolution of the cosmic microwave background in the frame of our Eulerian theory of cosmic lattice.
4.4. Quantum Physics, Particles Spin and Photons
The fourth section is dedicated to the quantum physics and the standard model of particles. One begins by using the second partial Newton equation, in the dynamical case, to show that there exists also longitudinal gravitational perturbations associated to moving topological singularities inside the lattice. By conjecturing operators similar to those of the quantum mechanics, one shows then that the second partial Newton equation allows one to deduce the gravitational fluctuations associated to a topological singularity moving quasi-freely with relativistic velocities within the lattice.
In the case of non-relativistic topological singularities bonded to a potential, one shows that the second partial Newton equation applied to the longitudinal gravitational fluctuations associated to these singularities leads to the Schrödinger equation of the quantum physics, which allows one for the first time to give a simple and realistic physical interpretation to the Schrödinger equation and to the quantum wave function: the quantum wave function deduced from the Schrödinger equation represents the amplitude and the phase lag of longitudinal gravitational vibrations associated to a topological singularity within the cosmic lattice!
All the consequences of the Schrödinger equation appear now with a simple physical explanation, as for example the stationary wave equation of a topological singularity placed inside a static potential, the Heisenberg uncertainty principle and the probability interpretation of the square of the wave function.
In the case where the gravitational fluctuations of two topological singularities are coupled, it appears also very simply the concepts of bosons and fermions, as well as the Pauli exclusion principle.
At the heart of a topological singularity loop, one shows that there cannot exist static solutions to the second partial Newton equation for the longitudinal gravitational fluctuations. It becomes then necessary to find a dynamical solution to this equation. The simplest dynamical solution is to imagine that the loop rotates around one of its diameter. By solving this rotation motion with the second partial Newton equation, which is nothing other than the Schrödinger equation, one obtains a quantified solution for the internal gravitational fluctuations of the loop. This solution is in fact nothing other than the quantic loop spin, which can take several different values (1/2, 1, 3/2, ∙∙∙) and which is perfectly similar to the spin of particles in the standard model! If the loop is composed of a screw disclination loop, it appears also a magnetic moment of the loop, proportional to the famous Bohr magneton. The notorious argument of the quantum physics pioneers wherein the spin cannot be a real rotation of the particle on itself because the equatorial velocity should become superior to light velocity, is swept out in our theory by the fact that the static expansion at the vicinity of the loop heart is so high that the light velocity becomes much higher than the equatorial rotation velocity of the loop!
In this argumentation about the absolute necessity of a spin of the singularity loops for satisfying the second partial Newton equation, only the exact value of the spin of a loop, namely 1/2 or 1, does not find at the moment a simple explanation!
One finishes by showing how to construct a pure transversal wave packet with a circular polarization and why it appears a quantification of the energy of these fluctuations. These waves packets form quasi-particles which have properties perfectly similar to the quantum properties of photons: circular polarization, zero mass, non- zero momentum, non-locality, wave-particle duality, quantum entanglement and quantum decoherence.
4.5. Standard Model of Elementary Particles and Strong Interaction
In a second part of the fourth section, one searches for the ingredients, which have to be added to the cosmic lattice in order to find an analogy between the loop singularities and the diverse particles of the standard model. One shows that, by introducing a cubic lattice with three families of planes (imaginary “colored” in red, green and blue), satisfying some simple rules concerning their successive arrangement and their mutual rotation, one can find topological loops perfectly analogous to all the particles, leptons and quarks, of the first family of elementary particles of the standard model. One finds also topological loops analogous to the W and Z bosons of the standard model. It appears spontaneously a strong force, in the sense that this force presents an asymptotical behavior, acting between the loops analogous to the quarks of the standard model, and which is due to the formation of a tube of stacking fault linking these loops. This implies that these loops have to group together in triplets to form combinations of three loops analogous to the baryons, or in doublets to form combinations of loop-anti-loop analogous to the mesons. Furthermore, one finds topological bicolor loops which correspond perfectly to the gluons associated to the strong force in the standard model!
In order to explain the existence of three families of quarks and leptons in the standard model, one shows that the introduction of more complicated topological structures of the edge dislocation loops, based on assembling of pairs of edge disclination loops replacing the edge dislocation loops, allows one to explain in a satisfactory way the existence of three, or even four, families of particles with very different energies.
Finally, one discusses the interest of this strong analogy between the topological singularities of a cubic “colored” lattice and the elementary particles of the standard model, as well as the numerous questions still pending concerning this analogy.
4.6. Vacuum Quantum State Fluctuations
The fifth section is dedicated to some very hypothetical consequences concerning the pure gravitational fluctuations associated to the perfect cosmic lattice. One can imagine the existence of pure longitudinal fluctuations within the cosmic lattice, which are not correlated with the presence of topological singularities, and which can be treated either as random gravitational fluctuations that could present some analogy with the vacuum quantum state fluctuations, or as stable gravitational fluctuations that could lead at the macroscopic scale to a cosmological theory of multiverse. At the microscopic scale, stable gravitational fluctuations could also lead to stable quasiparticles which could be called gravitons, by analogy with the photons, but which have nothing common with the gravitons postulated in the frame of the general relativity.
One finishes the book by a general conclusion in which one shows the central roles played by the Newton equation and by the microscopic structure of the cosmic lattice. One highlights also the numerous positive points, but also the still misunderstood points, which have appeared throughout this essay concerning the analogy between the Newtonian cosmic lattice and all the theories of modern physics.
5. Conclusions
It is remarkable that the description, using Euler’s coordinates in an absolute space-time frame, of a massive elastic “colored” cubic 3D-lattice containing loop topological singularities and having particular elastic properties allows one to find all observed natural phenomena.
In fact, the theory described in the book [2] [3] and summarized here is not yet completed, as there remain several questions without answers, as for example the exact nature of the “colored” 3D-lattice and its relation with the Higgs field postulated in standard model, the detailed rotation mechanisms of the topological loops and the reason for spin values of 1/2 or 1, and still several other unsolved problems detailed in the book.
However, it appears that this theory is the first and only 1) to combine all known physics in a very simple manner, unifying electromagnetism, relativity, gravitation and quantum physics, 2) to give a simple meaning to the local space-time and the quantum behavior of topological singularities, 3) to find a new scalar curvature charge which allows very simple explanations of the weak asymmetry observed between matter and anti-matter, of the nuclear weak interaction, of the formation of galaxies, of the disappearance of antimatter, of the formation of gigantic black holes in the heart of the galaxies, and of the famous dark matter, 4) to propose simple explanations to well-known problems of modern cosmology, as for example the universe expansion, the big-bang and the dark energy, and 5) to propose a model of “colored” cubic 3D-lattice whose diverse microscopic loop singularities correspond exactly to each of the elementary particles of the three families of particles of the standard model, and which allows to give a simple structural explanation to the strong force.
Acknowledgements
I would like to thank Gianfranco D’Anna, Marc Fleury, Daniele Mari and Willy Benoit for providing valuable input and comments, and Marc Fleury for his English translation of the book.