A New Second Order Numerical Scheme for Solving Forward Backward Stochastic Differential Equations with Jumps ()
Received 1 April 2016; accepted 26 July 2016; published 29 July 2016

1. Introduction
Bismut (1973) studied the existence of the linear backward stochastic differential equation, the results could be regarded as a promotion of a famous Girsanov theorem. The existence and uniqueness of solutions for nonlinear backward stochastic differential equations (BSDEs) were first proved by Pardoux and Peng (1990).Since then, BSDEs have been extensively studied by many researchers. In [1] , Peng obtained the relation between the backward stochastic differntial equation and the parabolic partial differential equation (PDE), and in Peng (1990), the stochastic maximum principle for optimal control problems were based on BSDEs. The applications of BSDEs now cover many scientific fields, such as stochastic control, stock markets, risk measure, turbulence fluid flow, biology, chemical reactions, partial differential equations, and so on. Thus it is very important and useful to obtain solutions of BSDEs for real applications. However, it is often quite difficult to obtain analytic solutions of BSDEs, so computing approximate solutions of BSDEs become highly desired, by using the relation between the BSDE and PDE. As far as we know, there have been very few schemes obtained with second-order convergence rate, such as [2] [3] .
In this paper, we propose a new second order numerical scheme for the solution of forward-backward sto- chastic differential qquations (FBSDE in short) with jumps with the following form
 (1)
(1)
From [4] , we know that the solution 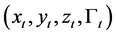 can be represented as
can be represented as
 (2)
(2)
where the vector function 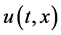 is the classical solution of the following parabolic differential equation (PDE) of the form
is the classical solution of the following parabolic differential equation (PDE) of the form
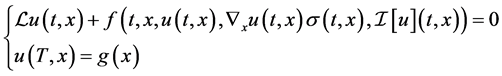 (3)
(3)
where 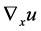 denotes the gradient of u with respect to the space variable x,
denotes the gradient of u with respect to the space variable x,
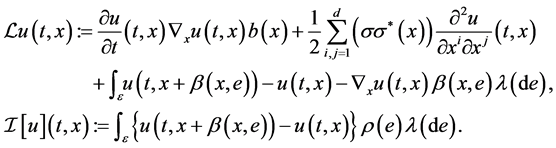 (4)
(4)
2. Preliminaries and Notation
Let T be a fixed positive number and 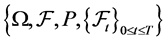 be a complete,filtered probability space on which is
be a complete,filtered probability space on which is
defined a standard Brownian motion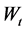 , such that
, such that ![]() is the natural filtration of the Brownian motion
is the natural filtration of the Brownian motion
![]() and all the P-null sets are augmented to each s-field
and all the P-null sets are augmented to each s-field![]() . Denote by
. Denote by ![]() the set of all
the set of all ![]() -adapted and mean-square-integrable processes.
-adapted and mean-square-integrable processes.
A process ![]() is called an
is called an ![]() -adapted solution of the FBSDE(1) if it’s
-adapted solution of the FBSDE(1) if it’s ![]() -adapted and
-adapted and ![]() -integrable, and satisfies (1). Under some standard conditions on the functions f and h, there is a unique adapted random process.
-integrable, and satisfies (1). Under some standard conditions on the functions f and h, there is a unique adapted random process.
Now we introduce a new probability space: for ![]() is an exponential martingale and satisfies
is an exponential martingale and satisfies
![]() , we define
, we define![]() . The random processes
. The random processes![]() , it is easy to verify that
, it is easy to verify that ![]() is an exponential martingale.
is an exponential martingale.
![]() (5)
(5)
Let us first introduce the following lemma.
Lemma 1. Given the time partition![]() , X is a
, X is a ![]() -measurable random variable,and satisfies
-measurable random variable,and satisfies![]() .
.
![]() (6)
(6)
We use the following Itô-Taylor approximation to solve the forward SDEs with jumps
![]() (7)
(7)
where
![]() (8)
(8)
and the coefficient function
![]() (9)
(9)
with
![]() (10)
(10)
Now we introduce some basic notations.
・ ![]() : the s-field generated by the Brownian motion.
: the s-field generated by the Brownian motion.
・ Throughout this paper, we denote by C a generic constant depending only on T, the upper bounds of the derivatives of the functions f.
3. Numerical Schemes for Solving BSDE
From the time interval![]() , we introduce the following time partition:
, we introduce the following time partition:![]() , let
, let
![]() and
and![]() . According to (1), it’s easy to obtain that for
. According to (1), it’s easy to obtain that for![]() ,
,
![]() (11)
(11)
From (5) and (11),we have
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
From (12), (13) and (14), by applying Itô formula to![]() , we obtain the equation
, we obtain the equation
![]() (15)
(15)
From (15), it is easy to obtain that for![]() ,
,
![]() (16)
(16)
Taking the conditional mathematical expectation ![]() on both side of the obtained equation, and by the nature of the conditional mathematical expectation,we deduce
on both side of the obtained equation, and by the nature of the conditional mathematical expectation,we deduce
![]() (17)
(17)
Based on (17), we have
![]() (18)
(18)
where
![]() (19)
(19)
and
![]() (20)
(20)
According to Lemma 1, the equality![]() , we have
, we have
![]() (21)
(21)
Let ![]() for
for![]() . Then
. Then ![]() is a standard Brownian motion with mean zero and vari- ance
is a standard Brownian motion with mean zero and vari- ance![]() . Now multiply (11) by
. Now multiply (11) by![]() , taking the conditional mathematical expectation
, taking the conditional mathematical expectation ![]() on both sides of the obtained equation, and using the Itô isometric formula, we deduce
on both sides of the obtained equation, and using the Itô isometric formula, we deduce
![]() (22)
(22)
From (22) we have,
![]() (23)
(23)
where
![]() (24)
(24)
Let![]() , similarly multiplying (11) by
, similarly multiplying (11) by ![]() yields
yields
![]() (25)
(25)
From (25) we have,
![]() (26)
(26)
where
![]() (27)
(27)
Based on (21), (23) and (26), for solving the BSDE (1) we propose the following scheme.
Scheme 1. Given![]() , solve
, solve ![]() backwardly by
backwardly by
![]()
4. Error Estimates
In this section, we will give the error estimates of Scheme 1 proposed in Section 3. Now we introduce the error
![]() ,
, ![]() and
and ![]() in
in ![]() norm, where
norm, where ![]() is the
is the
solution of the FBSDEs (1), and ![]() is the solution of Scheme 1. For the sake of simplicity, we only consider one-dimensional BSDEs
is the solution of Scheme 1. For the sake of simplicity, we only consider one-dimensional BSDEs![]() . However, all error estimate that we obtain in the sequel also hold for general multidimensional BSDEs. In our error analysis, we will use a constraint on the time partition step
. However, all error estimate that we obtain in the sequel also hold for general multidimensional BSDEs. In our error analysis, we will use a constraint on the time partition step![]() :
:
![]() (32)
(32)
Let us introduce the following Lemma, its proof can be found in the reference [2] .
Lemma 2. Let![]() ,
, ![]() and
and ![]() (
(![]() ) be the truncation errors defined in (21), (23) and (26), respec- tively. It holds that
) be the truncation errors defined in (21), (23) and (26), respec- tively. It holds that
![]() (33)
(33)
![]() (34)
(34)
Here C is a positive constant depending on T. We first give the error estimate for ![]() in the following theorem.
in the following theorem.
Theorem 1. Let ![]() (
(![]() ) be the solution of the FBSDE (1) and
) be the solution of the FBSDE (1) and
![]() be the solution of Scheme 1. Assume
be the solution of Scheme 1. Assume![]() . Then for sufficiently small time step
. Then for sufficiently small time step![]() , we have
, we have
![]() (35)
(35)
for![]() , where C is a constant depending on T.
, where C is a constant depending on T.
Proof. Let![]() . Subtracting (29) from (21) to get
. Subtracting (29) from (21) to get
![]() (36)
(36)
Under the conditions of the theorem and by Lemma 2,we deduce that,
![]() (37)
(37)
where L is the Lipschitz constant of ![]() with respect to y. Applying the inequality
with respect to y. Applying the inequality
![]() for
for ![]() with
with![]() ,
,
![]() , and
, and![]() , we deduce,
, we deduce,
![]() (38)
(38)
which by the inequality ![]() gives
gives
![]() (39)
(39)
Taking the mathematical expectation on both sides of (35), for sufficiently small ![]() we have
we have
![]() (40)
(40)
for![]() . The terminal condition
. The terminal condition![]() , the time step constraint (28) and the inequality
, the time step constraint (28) and the inequality
![]() (41)
(41)
lead to ![]() for
for![]() . The proof is completed.
. The proof is completed.
Then we turn to estimating the error![]() .
.
Theorem 2. Let ![]() be the solution of the FBSDE(1) and
be the solution of the FBSDE(1) and ![]() be the solution of Scheme 1. Assume
be the solution of Scheme 1. Assume![]() . Then for sufficiently small time step
. Then for sufficiently small time step![]() , we have
, we have
![]()
for![]() ,where C is a constant depending on T.
,where C is a constant depending on T.
Proof. Let![]() . From (19) and (25), we get
. From (19) and (25), we get
![]()
By Lemma 2, the inequality ![]() and Hölder’s inequality, we deduce
and Hölder’s inequality, we deduce
![]() (42)
(42)
where ![]() is a positive number which depends on p and the constant C in Lemma 2. Taking the mathematical expectation on both sides of the Equation (38) gives
is a positive number which depends on p and the constant C in Lemma 2. Taking the mathematical expectation on both sides of the Equation (38) gives
![]() (43)
(43)
by using Theorem 1 and constraint (28), leads to ![]() for
for![]() . The proof is completed.
. The proof is completed.
At last, we estimate the error![]() .
.
Theorem 3. Let ![]() be the solution of the FBSDE(1) and
be the solution of the FBSDE(1) and ![]() be the solution of Scheme 1. Assume
be the solution of Scheme 1. Assume![]() . Then for sufficiently small time step
. Then for sufficiently small time step![]() , we have
, we have
![]() (44)
(44)
for![]() , where C is a constant depending on T.
, where C is a constant depending on T.
Proof. Let![]() . From (26) and (31),we get
. From (26) and (31),we get
![]() (45)
(45)
By Lemma 2, the inequality ![]() and Hölder’s inequality, we deduce
and Hölder’s inequality, we deduce
![]() (46)
(46)
where ![]() is a positive number which depends on p and the constant C in Lemma 2. Taking the mathematical expectation on both sides of the Equation (42) gives
is a positive number which depends on p and the constant C in Lemma 2. Taking the mathematical expectation on both sides of the Equation (42) gives
![]() (47)
(47)
by using Theorem 1 and constraint (28), leads to ![]() for
for![]() . The proof is completed.
. The proof is completed.