Received 1 June 2016; accepted 24 June 2016; published 27 June 2016

1. Introduction
Let 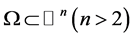 be a bounded domain. Assume
be a bounded domain. Assume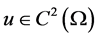 , we consider the Laplacian equation
, we consider the Laplacian equation
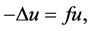
where 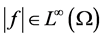 and
and 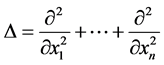 with
with . This is a second order differential
. This is a second order differential
equation. If 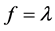 is a constant, then u is an eigenfunction with eigenvalue
is a constant, then u is an eigenfunction with eigenvalue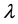 . By a standard Moser’s iteration in [1] - [5] , we have
. By a standard Moser’s iteration in [1] - [5] , we have 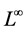 interior estimates of u controlled by the
interior estimates of u controlled by the 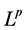 norm of u for
norm of u for![]() . In this paper, we use heat flow to consider the
. In this paper, we use heat flow to consider the ![]() estimate and give a new proof of the
estimate and give a new proof of the ![]() estimates without using iteration. First, we recall the definition of the heat kernel. For any
estimates without using iteration. First, we recall the definition of the heat kernel. For any ![]() and
and![]() , let
, let
![]()
be the heat kernel in![]() . For fixed
. For fixed![]() , we know that
, we know that
![]()
where ![]() is the standard Laplacian in
is the standard Laplacian in ![]() with respect to x. Our main result is the following
with respect to x. Our main result is the following
Theorem 1. Let ![]() be a bounded domain with
be a bounded domain with![]() . Assume
. Assume ![]() and
and
![]()
on ![]() with
with![]() . Then for any
. Then for any ![]() and any compact sub-domain
and any compact sub-domain![]() , we have the interior
, we have the interior ![]() estimate
estimate
![]() (1)
(1)
where ![]() is the distance of
is the distance of ![]() and the boundary of
and the boundary of![]() .
.
Remark 2. Following from the proof, one can consider equation ![]() or
or ![]() by choosing appropriate kernel function
by choosing appropriate kernel function![]() .
.
2. Proving the Theorem
To estimates on![]() , by the translation invariant and scaling invariant of the estimates, we only need to consider
, by the translation invariant and scaling invariant of the estimates, we only need to consider ![]() and
and![]() . By using heat flow, we have the following lemma.
. By using heat flow, we have the following lemma.
Lemma 1. Let ![]() be a unite ball. Assume
be a unite ball. Assume ![]() and
and
![]()
on ![]() with
with![]() . Then for any
. Then for any![]() , we have the interior
, we have the interior ![]() estimate
estimate
![]() (2)
(2)
Proof. Let ![]() be a standard smooth cutoff function with support in
be a standard smooth cutoff function with support in ![]() and
and ![]() on
on![]() , moreover,
, moreover,![]() . For any
. For any![]() , let
, let
![]()
By the heat equation![]() , integrating by parts, we have
, integrating by parts, we have
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
where we use integrating by parts for term ![]() to get (7) from (6). By direct estimate, since
to get (7) from (6). By direct estimate, since ![]() for
for ![]() and
and![]() , then
, then![]() . Therefore, for
. Therefore, for![]() , we have
, we have
![]()
Hence, for ![]() and noting that
and noting that![]() , we have
, we have
![]()
Since![]() , then we have
, then we have
![]()
By the property of heat kernel, we have![]() . Then we have
. Then we have
![]()
On the other hand, as![]() , we have
, we have
![]() (9)
(9)
Combining with![]() , we have
, we have
![]()
Hence we finish the proof.
The following lemma is fundamental.
Lemma 2. For any ![]() and any
and any![]() , we have
, we have
![]()
Proof. Let ![]() and
and![]() . Then
. Then
![]() (10)
(10)
![]() (11)
(11)
Now we are ready to prove Theorem 1.
Proof of Theorem 1. Refmaintheorem. For any compact subset![]() , let
, let![]() . For any
. For any![]() , we have
, we have![]() . Consider equation
. Consider equation
![]()
on![]() . By Lemma 1, since the estimates are scaling invariant, we have
. By Lemma 1, since the estimates are scaling invariant, we have
![]()
If![]() , then
, then![]() . By Lemma 2, we have
. By Lemma 2, we have
![]()
Hence we finish the proof.
Acknowledgements
The research is supported by National Natural Science Foundation of China under grant No.11501027. The first author would like to thank Dr. Wenshuai Jiang, Xu Xu for many helpful conversations.