Estimation of the Piecewise Exponential Model by Bayesian P-Splines via Gibbs Sampling: Robustness and Reliability of Posterior Estimates ()
Received 1 April 2016; accepted 19 June 2016; published 22 June 2016

1. Introduction
In several bio-statistical applications on censored follow-up time data, the interest lies mainly on the prognostic role of clinical/biological covariates. To such end, non-parametric and semi-parametric methods have been preferred over parametric ones. The most widely adopted tool is the Cox model, which avoids any assumption of the functional form of the hazard function on time. However, such feature is not useful if the interest lies on investigating the shape of the hazard or in predictive modeling. A solution was to include a flexible expression of the hazard function directly in the likelihood function for survival models (e.g. [1] - [3] ): this was considered since 1995 by Herndon and Harrell, who used restricted cubic splines ( [4] ).
Spline functions require the definition of the number of basis and position of spline knots. This can be difficult when the phenomenon under investigation presents complex features, such as a non-monotonic shape of the hazard with multiple peaks, or time dependent covariate effects. Penalized splines (P-splines) may be of advantage, since they avoid an arbitrary definition of spline bases, by using a high number of bases and eventually knots placed on a grid of equally spaced points. Furthermore, the degree of smoothing is controlled by regularized estimation, thus reducing the effective number of model degrees of freedom, and, therefore, giving a systematic method for the bias variance trade-off. Different kinds of penalization can be applied, potentially giving different results. The most common method has been proposed by Eilers and Marx ( [5] ), based on B-splines regularized with finite difference penalty functions (also called “roughness penalties”).
Penalized methods for estimating survival models have been described in the frequentist framework by Kauermann ( [6] ), amongst others. The proposal is based on specifying the hazard function through flexible polynomials, including directly such function in the likelihood function for survival data, and treating the coefficients of the polynomials as random effects. This approach allows resorting to the relationship between P-splines and mixed model theory (cfr: [7] ). However, the implementation of the above method can be cumbersome, because it requires the maximization of a likelihood function that includes a complex integral without a closed-form solution.
For what concerns penalized estimation methods in general, the confidence intervals based on the multivariate normal distribution of the estimates have unsatisfactory performances, because of penalty-induced biases (cfr: [8] ). Imposing a determined penalty is equivalent to specify some prior belief about the characteristics of the best model. In fact, the penalty makes explicit the fact that smooth models are believed to be more likely than “wiggly” ones. This has been a motivating rationale to use Bayesian methods ( [9] [10] ).
Bayesian P-splines have been introduced by Lang and Brezger ( [11] ). Fahrmeir and Hennerfiend ( [12] ) discuss their implementation in survival analysis. Dedicated routines are available, for example, in the software package BayesX ( [13] ). In such a context, point and interval estimates of model parameters and survival functions may be obtained in a straightforward way from posterior density samples. To this aim, Markov Chain Monte Carlo (MCMC) methods are needed, but they require efficient sampling algorithms in order to guarantee convergence of the Markov chains, and may be computationally intensive. The estimation method in [12] also deals with the survival likelihood, and, thus, shares the problem of the intractability of the cumulated hazard with the previously cited frequentist methods. In order to solve this problem, specific sampling schemes have been adopted for computation. Therefore, a dedicated software must be used to fit models in practice.
In order to make available a more user-friendly approach to researchers, we considered estimation of Piecewise Exponential (PE) models by Bayesian P-splines methods. Spline functions can be used in PE, which offer a compromise between a semi-parametric and a full parametric model based on weak distributional assumptions. That is, an exponential distribution within fixed time intervals for the time to event. The method of Eilers and Marx was developed in the context of generalized linear models (GLM): thus, it is suitable for PE models, because of their link with the Poisson distribution (GLM family of distributions). The PE family of models has been a basic block in past works ( [14] [15] ) for developing useful strategies of model building and assessment in the competing risks setting. Recognizing the advantage of penalized splines, recently ( [16] ) we described in detail the specification of a Bayesian PE model with a hazard function modeled by penalized splines for the analysis of univariate survival times. The model is analogous to the general model in [12] , but it is provided of a tractable likelihood function. In contrast with earlier approaches, the model can be fitted through general routines for estimating GLM hierarchical models: therefore, general Bayesian software can be used for computation.
In [16] , we described the implementation of Bayesian P-splines method for obtaining estimates of the hazard, of regression coefficients and survival probabilities. Examples have been given of estimation of models with a second order difference penalty and two distinct priors for the smoothing parameter. In this work we considered an extended expression of the model above, allowing regularized estimation of non-linear and time-varying effects of prognostic factors. Furthermore, we extended the evaluation of the robustness of the Gibbs sampling estimation method. To such end, we fitted several competing models, with different combinations of penalties and a more extensive set of prior densities, to two datasets, from breast cancer and soft tissue sarcoma patients, respectively. The adequacy of the competing models was assessed through the deviance information criterion (DIC) ( [17] ) using the standard expression for Poisson regression models. Furthermore, the reliability of the method was preliminarily evaluated by comparing the estimates of the hazard function on a large case series (breast cancer dataset) against benchmark clinical situations derived from literature: i.e. papers on tumor dormancy in breast cancer (cfr: [18] [19] ).
The remainder of this paper is organized as follows. In the method section we illustrate the construction of a general PE model with smooth components for the baseline hazard function, non-linear and/or time-varying effects of covariates. The smooth components above were specified following Eilers and Marx’s approach ( [5] ). In the subsequent section, results are presented concerning the evaluation of the robustness and the reliability of the estimates. Finally, conclusions and open issues are discussed.
2. Methods
In this section, a brief illustration of the characteristics of the standard PE model, with particular attention to the link with Poisson regression models, is firstly provided. Subsequently, methods for penalized estimation are reviewed. After this, the Bayesian P-splines estimation method is illustrated, and the general expression of the Bayesian PE models is illustrated. The section ends with two sub-sections concerning, respectively, the practical implementation of Bayesian P-splines and the definition of the DIC.
2.1. Simple PE Model
For univariate, possibly right-censored, survival data, let (Ui, Ci) be the random variables indicating, respectively, failure time and censoring time of the i-th subject. The observed data is represented by: ti = min(ui, ci) and by the status: vi:vi = 0 if ti = ci and 1 if ti = ui. Let Xi (p × 1 vector) indicate the set of covariates of subject i recorded at the beginning of the study. In the standard PE model the follow-up time is partitioned into a fixed set of H intervals: {Th = [τh−1, τh); τ0 = 0,  } and it is assumed that the time to failure U has an exponential distribution within each interval, whose parameters depend on the time intervals and the covariates. In the simplest case of proportional hazards, the relationship between the hazard function of the PE model and the covariates:
} and it is assumed that the time to failure U has an exponential distribution within each interval, whose parameters depend on the time intervals and the covariates. In the simplest case of proportional hazards, the relationship between the hazard function of the PE model and the covariates: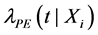 ; is expressed as follows:
; is expressed as follows:
 (1)
(1)
where: 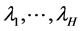 are the unknown parameters of the baseline hazard function;
are the unknown parameters of the baseline hazard function;  is the p × 1 vector of regression coefficients; and I(tÎTh) is an indicator function being equal to 1 if τh−1 ≤ t < τh and 0 otherwise.
is the p × 1 vector of regression coefficients; and I(tÎTh) is an indicator function being equal to 1 if τh−1 ≤ t < τh and 0 otherwise.
For right censored data the likelihood function has the general form:
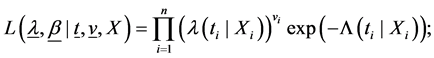 (2)
(2)
where t is a vector of n observed times, v a vector of the corresponding status, and the n × p matrix X represent
the covariates. The function 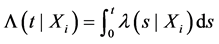 is the cumulative hazard. This likelihood resembles the
is the cumulative hazard. This likelihood resembles the
likelihood of a Poisson random variable Vi, with mean parameter . By substituting
. By substituting  in expression (2) with
in expression (2) with  (expression (1)), the likelihood becomes:
(expression (1)), the likelihood becomes:
 (3)
(3)
where for each subject i there is a product of Hi terms, Hi being the number of intervals in which the subject is followed. In the expression above, vih is the status of the i-th subject within the interval Th (0 = alive or censored, 1 = failed); Δih is the time spent in Th by the subject.
From expression (3) it may be seen that LPE is proportional to the product of Poisson likelihoods for Vih with mean parameters: . As a consequence, the expression of the Poisson regression model is:
. As a consequence, the expression of the Poisson regression model is:
 (4)
(4)
where αh = log(λh) are log-hazard parameters, and the term log(Δih) is an offset.
For fitting the PE model through model (4) as Poisson regression model, an augmented dataset must be derived from the original one. To such end, the data of each subject needs to be replicated for each interval in which it is followed. For each replicate, a row data indicating subject covariates, time interval and the status of the subject within the interval must be created for . Also, H dummy variables must be included for estimating the parameters αh. Time varying effects of, say, a variable Z1, may be easily included through a product of the dummy variables above and Z1. For more details about the PE model we refer to Rodríguez-Girondo et al. ( [20] ) and to the textbooks of Lawless ( [21] ) and Congdon ( [22] ) for more methodologically oriented discussions.
. Also, H dummy variables must be included for estimating the parameters αh. Time varying effects of, say, a variable Z1, may be easily included through a product of the dummy variables above and Z1. For more details about the PE model we refer to Rodríguez-Girondo et al. ( [20] ) and to the textbooks of Lawless ( [21] ) and Congdon ( [22] ) for more methodologically oriented discussions.
2.2. Hazard Smoothing
To obtain an interpretable shape of the hazard, a method for smoothing the time terms of the piecewise linear predictors is needed. Spline functions are the widest applied approaches. A spline function is a flexible polynomial constructed by joining ordinary polynomials within a set of intervals. For the time to event T, let’s consider a generic partition of the range of possible values formed by a set of K adjacent intervals, say: ; the extremes of the intervals are called knots. A spline of degree p may then be written as:
; the extremes of the intervals are called knots. A spline of degree p may then be written as:
![]()
where Pj(t;p) are polynomials of the same degree p. Usually, specific constraints are used for guaranteeing the continuity of spf(t;p) in the knots, so that to impose a smooth shape to the function.
Several classes of splines have been proposed in literature. Basis splines (B-splines) are the most widely used by statisticians, because of their favorable properties ( [23] ). The general expression of a B-spline is:
![]() (5)
(5)
where: ![]() is a M × 1 vector of spline bases, and
is a M × 1 vector of spline bases, and ![]() is the vector of
is the vector of
associated coefficients (M × 1). The expressions of the bases Bj(t; p) for differing values of p are derived by a recursive formula that is not of interest here. Usually, cubic splines are considered.
In regression models, the amount of flexibility of the splines depends on their degree and on the number of knots. However, increasing the flexibility of the splines does not always guarantee a better fit of the “true” hazard. The motivation, in brief, is that estimation of models that include too complex splines leads to a better interpolation of data, but at the same time it could reduce the reliability of the estimates. In other words, a too complex spline function approximates “signal plus noise” while it should give a good estimate of the signal only. This issue is commonly known as overfitting (see: [24] [25] ). On the other hand, a too simple spline leads to biased estimation: therefore, a method for choosing an optimal compromise between bias and overfitting is necessary.
To such end, penalized splines (P-splines) have been proposed in the GLM regression context by Eilers and Marx ( [5] ). The method is based on penalized estimation of the coefficients of B-spline functions using finite difference penalties (or roughness penalties). It may be applied in a natural fashion for regularizing the estimates of the hazard function. In the PE model, the baseline hazard function is piecewise constant. Such a function is a particular case of B-splines, given for p = 0. Thus we can write for each h:![]() , and substituting this term in expression (4). Thus for applying Eilers and Marx’s method, a penalization term on the coefficients
, and substituting this term in expression (4). Thus for applying Eilers and Marx’s method, a penalization term on the coefficients ![]() is needed. By referring to the GLM model (4), the estimates are determined by maximizing the penalized log-likelihood
is needed. By referring to the GLM model (4), the estimates are determined by maximizing the penalized log-likelihood![]() :
:
![]() (6)
(6)
where ![]() is the log-likelihood for model (4), φ2 is a smoothing parameter, and Dd repre-
is the log-likelihood for model (4), φ2 is a smoothing parameter, and Dd repre-
sents the finite differences operator of order d:![]() . More specifically, Δd is defined as
. More specifically, Δd is defined as
the functional that maps any variable into its finite differences: for d = 1:![]()
![]() ; for d = 2:
; for d = 2:![]()
![]() ; for a generic value of d:
; for a generic value of d:
![]() ;
; ![]() Therefore, since stronger irregularities of the hazard correspond to
Therefore, since stronger irregularities of the hazard correspond to
higher finite differences of the parameters αh, the “effect” of the penalty term:![]() ; on the pe-
; on the pe-
nalized log-likelihood function consists in supporting models with more regular hazard shapes over models with more irregular ones (expression (6)). The smoothing parameter φ2 is an additional parameter required for “tuning” the trade-off between model fit and model smoothness.
2.3. Bayesian P-Splines
The Bayesian P-splines method ( [11] ) is based on a hierarchical model for expression (4) with non informative priors for the regression coefficients ![]() and a Gaussian Random Walk (RW) prior of order d for the coefficients of the hazard function (B-spline), conditional to a smoothing parameter τ2. The general expression of the RW prior is the following:
and a Gaussian Random Walk (RW) prior of order d for the coefficients of the hazard function (B-spline), conditional to a smoothing parameter τ2. The general expression of the RW prior is the following:
![]() (7)
(7)
where:![]() . By assuming τ2 = 1/φ2, the argument of the exp() function above closely resembles the penalty term in expression (6).
. By assuming τ2 = 1/φ2, the argument of the exp() function above closely resembles the penalty term in expression (6).
By indicating the RW prior with the term: RW(τ2, Pd), a general expression of the PE model with a regularized hazard function is:
![]() (8)
(8)
where: B0 is the vector form of a B-spline of degree 0 defined on the intervals: ![]() of the follow-up period, and
of the follow-up period, and ![]() and
and ![]() are generic prior densities for the regression coefficients and the smoothing parameter. Further details on these priors will be given in a following subsection. For the former prior, univariate diffuse Gaussian densities are typically used in literature. For
are generic prior densities for the regression coefficients and the smoothing parameter. Further details on these priors will be given in a following subsection. For the former prior, univariate diffuse Gaussian densities are typically used in literature. For![]() , the most common choice is an inverse-gamma density with a high variance. However, in principle every prior for variance parameters in hierarchical models could be used ( [26] ). Furthermore, it has been pointed out (e.g.: [27] ) that the choice of
, the most common choice is an inverse-gamma density with a high variance. However, in principle every prior for variance parameters in hierarchical models could be used ( [26] ). Furthermore, it has been pointed out (e.g.: [27] ) that the choice of ![]() may have an unwanted influence on the posterior estimates: thus a sensitivity analysis is recommended in effective applications.
may have an unwanted influence on the posterior estimates: thus a sensitivity analysis is recommended in effective applications.
The expression above defines a hierarchical (mixed effect) Poisson model where the log-hazard parameters: ![]() are treated as random effects. The estimation of this model may be carried out by general MCMC sampling algorithms for hierarchical GLM models. In particular, software based on Gibbs sampling (e.g. WinBUGS) are an adequate choice, which facilitates the application of a global strategy for building useful models. We provided elsewhere the code for the estimation of model (8) through WinBUGS; other examples have been given as accompanying material for the paper by Murray et al. ( [28] ).
are treated as random effects. The estimation of this model may be carried out by general MCMC sampling algorithms for hierarchical GLM models. In particular, software based on Gibbs sampling (e.g. WinBUGS) are an adequate choice, which facilitates the application of a global strategy for building useful models. We provided elsewhere the code for the estimation of model (8) through WinBUGS; other examples have been given as accompanying material for the paper by Murray et al. ( [28] ).
2.4. General PE Model with Smoothed Components
Expression (8) may be easily extended for penalized estimation of possible non-linear and/or time-dependent effects of covariates, by including in the model expression, for each covariate, a basis spline function (B-spline polynomial) and an additional RW prior for each covariate. From now on, we will indicate with: ![]() the covariates with time-dependent effects; by
the covariates with time-dependent effects; by ![]() the covariates with non-linear effects, and with X the matrix including the values of covariates with unpenalized effects. The general expression of the PE model with regularized effects is the following:
the covariates with non-linear effects, and with X the matrix including the values of covariates with unpenalized effects. The general expression of the PE model with regularized effects is the following:
![]() (9)
(9)
The time-dependent effects for each covariate are:![]() ;
;![]() . Thus, for each Z1j, its values
. Thus, for each Z1j, its values
multiplied for a piecewise constant function:![]() ; in the parameters
; in the parameters![]() . This enables the
. This enables the
effect of each Z1j to vary in each interval Th of the original partition of the follow-up: ![]() for tÎTh. On the other hand, the effects of
for tÎTh. On the other hand, the effects of ![]() have been represented trough the general expression of B-splines (expression (5)), with the vector
have been represented trough the general expression of B-splines (expression (5)), with the vector ![]() including the spline basis of Z2l calculated for the i-th individual. Thus, in this case the degree and the knots of each spline are fixed following conventional rules (cfr: [5] ).
including the spline basis of Z2l calculated for the i-th individual. Thus, in this case the degree and the knots of each spline are fixed following conventional rules (cfr: [5] ).
2.5. Implementation Details
A more detailed discussion is needed concerning the implementation of RW priors in software. From expression (7) it may be seen that RW priors are essentially multivariate Gaussian priors with mean vector 0 and covariance matrix![]() . However, the matrix Pd is rank-deficient. To justify this statement, we recall that
. However, the matrix Pd is rank-deficient. To justify this statement, we recall that![]() , where Dd is the finite difference matrix of order d. The rank of Pd equals the rank of Dd (since rank(MTM) = rank(M) ; M being a generic n × k matrix), and Dd is generally not full-rank, due to the properties of the finite difference operators.
, where Dd is the finite difference matrix of order d. The rank of Pd equals the rank of Dd (since rank(MTM) = rank(M) ; M being a generic n × k matrix), and Dd is generally not full-rank, due to the properties of the finite difference operators.
For the reasons above, the standard densities available in software does not apply to the RW prior. In alternative one can use the CAR function, which is specifically designed for Gaussian autoregressive stochastic processes, and is available in WinBUGS (cfr: [29] ). Another alternative that does not require specific software consists in a reparameterization of the hazard parameters ![]() in two independent vectors with full-rank covariance matrices and regular prior densities (see: [30] for details). The reparameterization is based on the following expression:
in two independent vectors with full-rank covariance matrices and regular prior densities (see: [30] for details). The reparameterization is based on the following expression:
![]() ;
;
where![]() ,
, ![]() are vectors of length d and H-d, and Ψ1, Ψ2 are matrices of dimensions H × d and
are vectors of length d and H-d, and Ψ1, Ψ2 are matrices of dimensions H × d and![]() , respectively. Thus, the dimensions of the terms above depends on the choice of the degree d of the penalty func-
, respectively. Thus, the dimensions of the terms above depends on the choice of the degree d of the penalty func-
tion. In particular, ![]() , whereas the expression of Ψ1 is obtained as follows, by matrix algebra
, whereas the expression of Ψ1 is obtained as follows, by matrix algebra
argumentations. A useful expression for deriving Ψ1 is: ![]() (required for guaranteeing the orthogonality of Ψ1 and Ψ2). This implies that the columns of Ψ1 form a basis for the null space of the finite difference operator Δd (section: hazard smoothing). In practice: for d = 1, the expression becomes:
(required for guaranteeing the orthogonality of Ψ1 and Ψ2). This implies that the columns of Ψ1 form a basis for the null space of the finite difference operator Δd (section: hazard smoothing). In practice: for d = 1, the expression becomes:![]() ;
;![]() . This implies: Δ1(Ψh) = 0; which is satisfied by:
. This implies: Δ1(Ψh) = 0; which is satisfied by:![]() . For d = 2, the condition: Δ2(
. For d = 2, the condition: Δ2(![]() ) = 0 is satisfied by
) = 0 is satisfied by ![]() and by another vector that includes a linear succession:
and by another vector that includes a linear succession:![]() . For higher values of d, the columns of Ψ1 will be obtained by including additional vectors,
. For higher values of d, the columns of Ψ1 will be obtained by including additional vectors, ![]() that will include successions of higher order.
that will include successions of higher order.
From the definitions above it follows that the parameters in ![]() have a flat prior density, whereas independent conditional Gaussian priors (conditional to τ2) must be assumed for the parameters in
have a flat prior density, whereas independent conditional Gaussian priors (conditional to τ2) must be assumed for the parameters in![]() . For example, the following expression shows an equivalent reformulation of model (8) that can be readily implemented in WinBUGS as like as in any other dedicated software:
. For example, the following expression shows an equivalent reformulation of model (8) that can be readily implemented in WinBUGS as like as in any other dedicated software:
![]() (10)
(10)
For more general models (expression (9)) the equivalent expressions are obtained straightforwardly.
2.6. Deviance Information Criterion
The DIC is a frequently used tool for comparing the adequacy of competing models (cfr: [17] ). For GLM models, it can be considered as a generalization of the Akaike Information Criterion (AIC), and thus it yields a ranking of competing models based on their predictive ability. The general expression is:
![]()
where: ![]() is the model deviance calculated in the posterior mean of the parameters:
is the model deviance calculated in the posterior mean of the parameters:![]() ,
, ![]() is a “measure” of the effective degrees of freedom. The DIC is a useful statistic for hierarchical models and, also, for penalized models, for which the traditional measures of model complexity does not apply. Furthermore, the DIC is calculated very easily from the output of Gibbs sampling software. For such reasons, we considered the DIC as an appealing tool for model comparison in this work.
is a “measure” of the effective degrees of freedom. The DIC is a useful statistic for hierarchical models and, also, for penalized models, for which the traditional measures of model complexity does not apply. Furthermore, the DIC is calculated very easily from the output of Gibbs sampling software. For such reasons, we considered the DIC as an appealing tool for model comparison in this work.
3. Results
3.1. General Plan of Analysis
The Bayesian P-splines method was applied to two datasets on breast cancer and soft tissue sarcoma patients (cfr: [31] [32] ). The covariates included in the models were fixed a priori and corresponded to well-known prognostic factors for the investigated outcomes. The partition of the follow-up time was based on routine clinical follow-up schedules. Moreover, previous experience on breast cancer patients analysis suggested us that narrower intervals do not improve the knowledge of disease dynamics. In the remainder application, there is a higher uncertainty about this issue; however the assumption of a constant hazard between consecutive patient visits is reasonable on clinical grounds.
For the breast cancer dataset only discrete covariates were included: age at diagnosis (≤35 years, 36 - 45 years, 46 - 55 years, 56 - 65 years, >65 years), tumor size (≤0.5 cm, 0.6 - 1.0 cm, 1.1 - 1.5 cm, 1.6 - 2.0 cm, >2.0 cm), nodal status (N−, 1 N+, 2 - 3 N+, ≥4 N+), histologic type (infiltrating intraductal component or infiltrating lobular component: IDC + ILC; extensive intraductal component: EIC; other histology) and tumor site (external, internal or central); according to the original study ( [31] ). The hazard function was expressed through basis functions (expression (10)). We considered both a model without time-varying covariate effects (that is, proportional hazards (PH) model), and a model with a time-varying effect of tumor size.
For each of the models above, the robustness of the estimation method was assessed in the following way: ten competing model expressions have been specified, including distinct combinations of priors for smoothing parameters and penalty matrices. The resulting estimates: posterior means and respective 95% credible intervals for the hazard and the regression coefficients have been compared by descriptive methods (tabulation, graphical representation). A more formal comparison was performed using the DIC.
The priors used for defining the competing models were: four inverse-gamma priors for the smoothing coefficients (τ2): Γ−1(a,a) with a = 1, 10−2, 10−4, 10−6; and a uniform prior: U(0,100) for τ. The penalties were specified through finite difference penalties of order 2 and 3. Furthermore, the reliability of the estimation method has been assessed, by comparing the behavior of the estimated hazards against benchmark clinical situations derived from literature ( [18] [19] ).
In the second application (soft tissue sarcoma), the covariates were: age (years) and tumor size (cm) (continuous variables), histologic subtype, grading and surgical margins (microscopic, macroscopic) (categorical variables). The classes of categorical covariates corresponded to those used in the original study ( [32] ). Concerning the shape of the hazard, there is no widely accepted knowledge: thus a PE model with a smoothed hazard function (without time-varying covariate effects) was used as a tool for exploratory analysis. The robustness of the estimation method has been assessed following the same strategy illustrated above.
In each application, MCMC sampling was performed by executing WinBUGS under R ( [33] ), via the R2WinBUGS package ( [34] ). Subsequent calculations were done in R with the coda package ( [35] ) added. Posterior estimates were obtained from single chains of length 20,000, with burn-in of 2000 and thinning by 5. Thus, the effective size of the posterior sample was 3600. In each case, standard diagnostic techniques showed appreciable mixing properties of the Markov Chains, and autocorrelations rapidly approaching zero.
3.2. Application 1: Breast Cancer Dataset
3.2.1. PE Model with a Smoothed Hazard Function
The sample included 2010 patients out of 2233 who underwent conservative surgery at Milan Cancer Institute between 1970 and 1987. The outcome considered here was event-free survival (which included: local recurrences, distant metastases, other primary tumor, death).
Due to the large sample size, a procedure for avoiding an excessive computational burden was required: recall that for fitting the PE model the original dataset must be augmented (methods section). We resorted to a “binning” approach (as, for example, in [36] ): the patients were grouped in K groups, identified by the K possible combinations of covariate values observed in the sample (bins). Then, a new dataset of K rows was constructed, including: the total number of subjects in the group; the number of observed events and the total follow-up times for the subjects above; and the set of covariate values corresponding to each bin. The PE models described in the following were then fitted to the binned datasets. The benefits of this procedure increase as the difference n (sample size) and K becomes higher.
For specifying the PE model with a smooth hazard function, the follow-up period was divided in 18 consecutive intervals of one year length. The covariates were all categorical. They were included in the expression of the model through dummy variables using the “reference category” coding. By indicating the dummy variables with the letter D, the linear predictor of the model: η = log(μ) was:
![]() (11)
(11)
where: AGE, TSIZE, NSTATUS, HIST and TSITE indicate, respectively: age at diagnosis, tumor size, nodal status, histologic type, and tumor site. The intercept corresponds to the first element of the vector ![]() (because the first column of Ψ1 is always a constant vector of ones). The model includes 33 parameters: 32 in the linear predictor (18 hazard parameters for the baseline hazard function and 14 for the regression coefficients) plus 1 smoothing parameter.
(because the first column of Ψ1 is always a constant vector of ones). The model includes 33 parameters: 32 in the linear predictor (18 hazard parameters for the baseline hazard function and 14 for the regression coefficients) plus 1 smoothing parameter.
Posterior means and 95% credible intervals of all the 33 parameters above were robust with respect to the priors and penalties used (Table A1). Since the PH parameterization of the model, for evaluating the shape of the hazard function any combination of the covariates included in the model can be considered. Thus, we reported in Figure 1 the estimated hazards from all the ten competing models previously described for a
![]() (a)
(a)![]() (b)
(b)
Figure 1. Estimated hazard functions for model (11). Panel (a): 5 models with distinct priors for the smoothing parameter and second order difference penalty; Panel (b): 5 models with the same priors and a third order difference penalty. Black solid lines: posterior means; dotted lines: 95% credibility intervals. Covariate values were: Age: ≤35 years, tumor size: 0.5 cm, nodal status: 4 N+, quadrant: external, histology: IDC + ILC.
fixed set of covariate values: age ≤ 35 years, tumor size ≤ 0.5 cm, nodal status = 4 N+, quadrant = external, histology = IDC + ILC). As it may be seen, the estimates were practically undistinguishable.
Concerning the clinical interpretation of the function, the shape resulting from Figure 1 showed a major peak within the third year of follow-up, followed by a non constant trend, in which two other peaks could be noticed. This behaviour is consistent with accepted clinical knowledge on breast cancer case series (e.g.: [18] [19] ), although the accuracy of estimates was rather low (especially in the later follow-up period).
A more formal evaluation of the ten competing models was performed through the DIC. From the values reported in Table 1, no relevant differences emerged in terms of model fit (deviance), effective degrees of freedom (pD) and therefore in terms of overall adequacy (DIC). Thus, in the present example the choice of different priors and/or penalties had a negligible influence on posterior sample estimates.
3.2.2. PE Model with a Time-Varying Effect of Tumor Size
The specification of the time-varying effect required to include extra basis functions (B-splines of degree 0) for the modalities of tumor size (expression 9). The expression of the linear predictor was specified as discussed in the following. In expression (9) the term: ![]() represents a piecewise constant hazard for patients with tumor
represents a piecewise constant hazard for patients with tumor
size lower or equal 0.5 cm (the reference category), whereas smooth terms of the form: ![]() would
would
represent (smooth) differences between the hazard of the remainder categories of tumor size (k = 1 - 4) and the previously indicated hazard. We considered more appealing to obtain smooth estimates directly for each hazard function: therefore, we slightly modified the expression:
![]()
into the following one:
![]() .
.
This was analogous to reparameterizing a two-way factorial ANOVA model with reference category coding
![]()
Table 1. Adequacy of the competing models for estimating model (11) Dbar = deviance; pD = effective degrees of freedom; DIC = Deviance Information Criterion.
for tumor size and cell means coding for follow-up time, into a model with cell means coding for both the “factors” above. The final expression of the linear predictor was made similar to expression (10):
![]() (12)
(12)
Due to the very low frequency of events observed at later times, the follow up was truncated to 15 years (instead of 18) for overcoming hard convergence problems of the Markov Chains. After this, a regular behaviour of the chains was shown in each case. Model (12) included a total of 90 parameters, divided in: 75 parameters for the time-varying effect of tumor size; 10 for other regression coefficients and 5 smoothing parameters.
As in the previous section, the estimates of all model parameters were robust with respect to priors and penalties. For sake of simplicity, results were reported for only one competing model (uniform prior for the smoothing parameters, second order difference penalty). The most evident time-varying effects of tumor size were shown comparing the hazard shapes for tumors sized ≤1.0 cm with the shapes for tumor size: from 1.1 - 1.5 cm to >2.0 cm (Figure 2). A high peak after the second year of follow-up emerged clearly only for tumor size ≥1.1. cm; a second evident peak may be seen at the 10th year of follow-up, for tumor size between 1.6 cm. and 2.0 cm. These characteristics are, again, consistent with the clinical experience. Even though the estimates for tumor size >2.0 cm were inaccurate. This outcome was likely due to a low number of events occurred in the later follow-up.
3.3. Application 2: Soft Tissue Sarcoma Data
Data were collected from a case series of 192 subjects affected by soft tissue sarcoma in care at Istituto Nazionale dei Tumori di Milano who underwent surgical resection of primary localized disease. The end-point of interest was time elapsed form surgery to death from any cause. Time was measured in months.
For specifying the PE model with a smooth hazard function, the follow-up period was divided in 15 intervals according to the schedule of patients control visits. The covariates were: age (years) and tumor size (cm) (continuous variables), histologic subtype, grading and surgical margins (microscopic, macroscopic) (categorical variables). Age was centered with respect to the mean (age), while a non linear effect of tumor size was modelled through a Restricted Cubic Spline with three knots. The expression of the smoothed PE model was then the following:
![]() (13)
(13)
![]()
Figure 2. Estimated hazard functions for model (12). Reported in the figure is the hazard function for a patient with the same covariates as in Figure 1, except for tumor size. Black solid lines: posterior means; dotted lines: 95% credibility intervals.
where: RCS1(tsize) and RCS2(tsize) indicate the spline bases of the restricted cubic spline for tumor size, orthogonalized for improving the efficiency of the MCMC sampling algorithm. The terms: HIST, GRADE, MARG, HIST; indicate, respectively, histologic subtype (Liposarcoma, Leyomiosarcoma: LEYO; MPNST, FST, Other), grading (1,2,3) and surgical margins (microscopic: MICRO; macroscopic: MACRO). The model included 26 parameters: 15 hazard parameters, 10 regression coefficients, and 1 smoothing parameter.
In Figure 3, we reported the estimated hazard function from the ten competing models. Given the PH structure of the model, the shape of the hazard was reported for a fixed set of covariate values: age = 55 years; tumor size = 20 cm; histology = liposarcoma; grading = 2; margin = microscopic. These functions showed distinct behaviors, thus evidencing the dependency of the results from the choice of the structural components of the model. For what concern the estimates of covariate effects, the values of posterior means and respective credible intervals were robust.
In the following table (Table 2), the competing models have been ranked according to the DIC. Little differences emerged among the models in terms of deviance (Dbar), while major ones were shown in terms of effective degrees of freedom (pD). More interestingly, it seems that the order of the penalty had not a relevant influence on model adequacy, and, thus, the priors had a leading role. Overall, the “best” models correspond to more diffuse priors.
4. Discussion
Several clinical studies are focused on pathologies with long follow up times, and on the prognostic effect of a large set of variables. The aim is to investigate disease dynamics by maintaining the maximum possible amount of the information included in the variables. Thus, continuous variables are included in the model in their original measurement scale. Biologically plausible interactions and time-varying effects also need to be considered. In such a way the model could be complex and penalized estimation methods could be useful tools. Our approach relies on the use of the Bayesian P-splines method for estimating of a PE model with a flexible specification of the baseline hazard, non-linear and/or time-dependent covariate effects. In the context of penalized estimation the Bayesian methodology provides a unified theoretical framework for all the inferential procedures.
![]()
Figure 3. Estimated hazard functions for model (13). Black solid lines: posterior means; dotted lines: 95% credibility intervals. Covariate values were: Age: 55 years; tumor size: 20 cm; histology: liposarcoma; grading: 2; margin: microscopic. On the left (panels: a, c, e, g, i) estimates from competing models with a second order difference penalty; on the right (panels: b, d, f, h, j) estimates from models with a third order difference penalty.
![]()
Table 2. Adequacy of the competing models for estimating model (13) Dbar = deviance; pD = effective degrees of freedom; DIC = Deviance Information Criterion.
This is an advantage over frequentist methods, where in the presence of penalties the standard large sample theory does not provide useful results for interval estimation.
Our approach has two main distinctive features with respect to the cited papers on the Bayesian P-splines method:
1) We focused the attention upon on the PE family of models, which did not require specific sampling algorithms or specific software for estimation.
2) Due to the link between PE models and the GLM family of regression models, several already available methods, such as the DIC, could be used for developing an efficient strategy of model building. Again, the implementation of such methods should not require, in principle, specific accommodations for computation.
The approach has several points in common with Fahrmeir and Hennerfiend’s method ( [12] ), and, also, with the approach more recently discussed by Murray et al. ( [28] ). In particular, the family of models considered in our work is a subset of the general model in [12] ; however, in our case the likelihood function is tractable, and, thus, specific solutions for approximating the integrated hazard are not needed. Also the model in [28] can be considered as a subset of the general model above, characterized by a piecewise linear hazard function and a tractable likelihood. In the cited paper, the estimates from this model slightly outperformed the PE model in simulations, even though for the latter a major robustness of the estimates emerged with sparse data. The major focus of the paper was on the performances of estimates, whereas a formal method of model assessment was not covered.
On the other hand, the major critics to the PE model are (e.g.: [28] ): 1) a piecewise constant hazard function is generally not “realistic”; 2) estimates of the hazards are sensitive to the partition of the follow-up time (number and length of intervals). Without any doubt we agree with the first remark. Notwithstanding, we advocate our approach as a useful one for exploratory assessment of the hazard function. In particular, the presence of discontinuities in the estimated hazard does not prevent from evidencing relevant features of the “true” hazard. Concerning the second critic, this one could not be a real issue. We recall that Eiler’s and Marx’s approach provide a mean for overcoming problems concerning the choice of spline bases and knots, by partitioning the range of the variables in a high number of intervals. However, as far as we know an effective study concerning the issue above has not been carried out yet in our context.
The results shown in this paper concern the estimation of “pre-specified” regression models (i.e.: models specified a priori according to validated clinical knowledge), in studies with long follow-up periods. In the first application (breast cancer) the data has been collected from a large case series. The estimates from several competing models, differing for the specification of their smoothing functions (using distinct combinations prior densities for the smoothing parameters and finite difference penalties), were practically undistinguishable. Also, no sensible differences emerged in terms of model adequacy, as indicated by the DIC cri1terion. These results emerged in the estimation of both a “simple” PE model with a smooth hazard function, and in a more complex model including smoothed time-varying effects of a covariate.
Since Bayesian P-splines require the specification of non-informative priors, the sensitivity of posterior estimates is an essential task in effective applications. As stated in the method section, the influence of the specific prior for the smoothed parameter has been evidenced in literature, and thus it was one of the primary objects of investigation in our works. For the breast cancer dataset, no relevant influence has been found. We hypothesized that the posterior density “converged” to the (penalized) likelihood function. This was checked by comparing the posterior estimates of all the parameters of the models above with the corresponding estimates obtained by GAM regression (via the mgcv package of R ( [37] ). We found a good overall agreement between the two methods; in particular, the GAM estimates of the hazard function closely overlapped the Bayesian ones.
The low frequency of events occurring at later follow-up times had some influence on the efficiency of the sampling algorithm: in fact, for estimating the model with time-varying coefficients we were forced to truncate the follow-up period to 15 years. However, MCMC diagnostics evidenced no further problems after this. Moreover, it is likely that the above scarcity of events affected the accuracy of the estimates of the hazard in the upper tail of the follow-up. Higher or more specific case series are needed for improving the “information content” of such estimates, whatever the specific estimation method or family of regression models adopted in the analysis.
Concerning the interpretation of the hazard function, the shape of the hazard resulting in the breast cancer data set was in agreement with clinical knowledge, thus suggesting that the estimation method has a good reliability in our example.
The application of the method on a relatively small case series (sarcoma dataset) yielded both positive and negative results. Concerning the former ones, the estimates of regression coefficients were robust with respect to the specification of the “structural components” of the regularized PE model (same as above). As emerged in previous work ( [16] ), this holds also for the estimates of the survival function. The “bad” result consists in the sensitivity of the posterior estimates of the hazard function with respect to the structural components of the model. In this application the prior density for the smoothing parameter was the major determinant of the differences between the competing models. An interesting result was that the estimates from the “best” model, according to the DIC criterion, were the most close to the corresponding estimates from GAM regression. This could be a good hint in favor of the utility of the DIC for picking up the best approximation of the underlying hazard; however, a more thorough investigation is needed concerning its effective performances.
5. Conclusions
Our approach provides a practical alternative for regularized estimation of survival regression models. The Gibbs sampling algorithm provides efficient computation of the posterior estimates in the examples reported here. General software routines may be used in real applications, thus facilitating the application of Bayesian P-splines to practitioners. Overall, the estimates are robust with respect to the choice of the components of the smoothing functions included in the model, and provide reliable results. The issue of the sensitivity with respect to the priors results to be limited to the estimates of the hazard function, and seems more only when a relatively small case series are under investigation.
Overall, the proposed method could be a useful tool for the flexible modeling of disease dynamics in complex frameworks like cancer follow-up studies.
Acknowledgements
This work was funded by the Italian Association for Cancer Research (AIRC). IG 2012 rif: 13420, “Statistical Tools for Prognosis and Prediction in Cancer: Assessments and Application to a Sarcoma Case Series”. EMB was Principal Investigator. GM was a fellow of AIRC. The authors thank Dr. Alessandro Gronchi for providing the data on the sarcoma case series.
Appendix 1
(a) ![]() (b)
(b) ![]()
Table A1. Estimates for application 1: Posterior means and 95% credible intervals (a) hazard parameters, second order difference penalty. (b) Regression coefficients, second order difference penalty.
NOTES
![]()
*Corresponding author.