Electromagnetic Modeling of a Planar Structure Integrating a Via-Hole Using the Method FWCIP

Sameh Toumi Sahli¹, Fethi Mejri², Taoufik Aguili¹

¹Syscom Laboratory, National Engineering School of Tunis, Tunis, Tunisia.
²Faculty of Sciences of Bizerte, Bizerte, Tunisia.

DOI: 10.4236/ojapr.2016.42006                

Abstract

We present in this paper a new formulation of the iterative method FWCIP “Fast Wave Concept Iterative Process” based on the wave concept. It calculates the electromagnetic parameters of a planar structure including a via-hole. This is modelled by the electromagnetic field that it creates in the structure. The validation of results found by this new formulation is ensured by comparison with those obtained by HFSS “high frequency structural simulator” software from Ansoft. They show that they are in good agreement.

Keywords

Microstrip Line, Iterative Method FWCIP, Impedance Input, Planar Structure, Via-Hole

Received 19 March 2016; accepted 14 June 2016; published 17 June 2016

1. Introduction

The field of microwave and hyperfrequency which are based on planar structures, has been known in recent years as a very high-demand and technological progress. The application domain now affects different areas from professional applications such as high-precision navigation systems for terrestrial and space communications, remote sensing, radar (civil and military) and radiometry. The communication hyperfrequency has many public applications such as television, mobile phones, radio, alarm systems and security [1] .

Indeed, the high cost of technology and time implemented for the realization of a function of analog electronics make the traditional approach impossible to test several models for testing arriving at the necessary improvements. The designer of microwave circuit must have a simulation tool to predict the performance of a component or a circuit operating in different conditions [2] .

We were interested in this work to planar structures incorporating a via-hole. This technique will allow better use of both sides of a printed circuit substrate. To model this structure the iterative method [3] has been reformulated to reflect the presence of the via-hole in the circuit. In this formulation the TE (Transversal Electric) modes, TM (Transversal Magnetic) and TEM (Transverse Electro-Magnetic) are used as digital basis of spectral domain in which the FFT (Fast Fourier Transform) [4] is projected. Subsequently, the concept of fast wave is introduced to reflect the boundary conditions and continuity of relationships in different parts of the interface in terms of waves. The iterative method consists of determining an effective relationship between the incident and reflected waves in different dielectric layers. The reflected waves are expressed in the modal domain and the incident waves in the space domain. The iterative process is then used to move from one field to another using the FMT (Fast Modal Transform) and to speed up the iterative process and then the convergence of the method. This formulation retains the well-known advantages of the iterative method including ease of implementation and speed of execution compared to other methods.

2. Reformulation of Method FWCIP

2.1. Representation of the Study Structure

The study of structure (Figure 1(a)) is a microstrip line dimensions (Lxw₁), connected to the ground through a via-hole of dimensions (h₂xw₂). The thickness of the line and the via-hole is assumed to be negligible. The excitation of the structure is provided by a source of localized electric fields S₀{E₀,J₀}. The plan W (Figure 1(b)) is located between two dielectric media, relative permittivities ε_r1 and ε_r2 supposed without losses.

Parameters of the study structure:

, , , , , , ,.

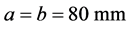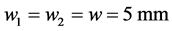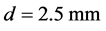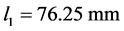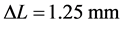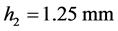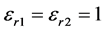W: Area (Or discontinuity plan) between the areas 1 and 2.

2.2. Formulation of the Problem

The analysis method is an iterative method. It has been described in various articles and thesis [5] - [7] . It is developed for modelling planar structures, single or multilayer, arbitrary shape, comprising passive or active components. It is based on two types of waves, incident (A_k) and reflected (B_k), respectively expressed in spatial and modal fields, relationships (1) and (2). The passage of these waves from one domain to another is provided by the iterative process using the FMT, which is none other than the weighted FFT on each mode. The use of the FMT, significantly reduces the computation time and accelerates the convergence of the method, but requires the description in pixels of different regions of discontinuity plan W. At any point of this interface is defined an associate wave vector of the electromagnetic field by:

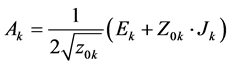(1)

Figure 1. Structure of study (a) and plan of discontinuity W (b).

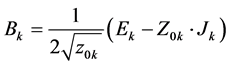(2)

with:

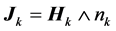, (3)

: Indicates the area 1 or 2 and n_k is a normal unit vector to W.

: Tangential components of the electromagnetic field.

: Impedance of the characteristic area k.

Operational equations on which this method is based are defined by:

n: Number of iterations.

: Incident wave initializing the iterative process, it is issued by an excitation source (level) on either side of the plane W.

: Diffraction operator giving the incident waves from the reflected waves in the spatial domain. It describes the boundary conditions and continuity of the different constituents regions plan W of structure.

: Modal reflection operator giving the waves reflected from the incident waves in the modal field, k is the area 1 or 2.

・ Area 1: described the nature of the walls of the box and the dielectric of the area 1 of the structure.

(6)

・ Area 2: described the nature of the walls of the box and the dielectric of the area 2 of the structure. It also introduces the influence of the electromagnetic field created by the via-hole in the area 2.

(7)

(8)

The phrase reflects the electromagnetic field of the n modes created by the via-hole in the area 2.

With:: Basic functions of box (in this case the box is in electrical walls).

: Admittance modes, upper and lower covers, reduced at the plane W.

The modes of the rectangular waveguide are given according to the nature of the walls in the following Table 1 and Table 2.

Let that: ,

Table 1. Function modes of a rectangular waveguide with electrical walls.

Table 2. Function modes of a rectangular waveguide with magnetic walls.

with:

The structure is divided into pixels, we will proceed to the following variable change:

and

N₀₁ and N₀₂ are the total number of pixels respectively according to (ox) and (oy).

・ If a top or bottom cover placed at a distance h from the discontinuity plane W.

・ For an open circuit (in the absence of the cover/guide infinity).

With: is the admittance of mode given for the modes:

: is the propagation constant expressed in the spectral domain according to the geometrical sizes and

different characteristic elements of the considered area k. It is expressed by the following equation:

: Basic functions of the via-hole.

: Reflection coefficients of the via-hole.

: Reflection coefficients modes of the via-hole.

: Electric field of fundamental mode of via-hole.

: Reflection coefficient of the fundamental mode.

, we have for the area 2: Þ Þ

: Intrinsic impedance of the area k.

: Vacuum impedance.

: Impedance of the mode TEM.

: Characteristic impedance, w is the width of the via-hole.

2.3. Modal Study of the via-Hole

We present in this section an analytical calculation of the electromagnetic field created by the via-hole in the area 2 (Figure 2).

To calculate the electric field created by the via-hole in the study of structure, we assume that it is placed in a rectangular waveguide with metal walls and filled with a dielectric substrate relative permittivity e_r2 (Figure 3). The via-hole and the waveguide are considered infinite in length to eliminate side effects. We also neglect the losses in the conductor and the dielectric thereby further simplifies the problem formulation.

The fundamental mode of propagation of such a support is not TEM because the cross section is not homogeneous. However, since the amplitudes of the longitudinal components of electric and magnetic fields are sufficiently small to be neglected, one thus speaks by quasi-TEM mode. This makes it then possible modeling of the structure in the form of a characteristic line impedance Z_c transmission immersed in an equivalent homogeneous medium characterized by an effective relative permittivity e_r2.

To define the position of the via-hole we split the area 2 of the structure into two regions “I” and “II” (Figure 2 and Figure 3).

2.3.1. Fundamental Electric Field Created by the Via-Hole

1) General formulas of the electric field created by the via-hole along the axis (ox), in the regions “I” and “II” by Figure 3 are defined by:

(9)

Figure 2. Presentation of the via-hole in the study structure (a) and the oxy plane (b).

Figure 3. Study structure to calculate the electric field created by the via-hole.

(10)

With the length of the metal strip and.

Or designate the amplitude of the mode (),and are the basic

functions of an infinite waveguide:

,

,

With si n = 0

si n ≠ 0

n: Modes indices TE and TM.

a: Box dimensions along the axis (ox).

b: Propagation constant.

2) The following field via-hole axis (oz) is written as follows:

(11)

(12)

Note: To calculate the electric field created by the via-hole we must begin by calculating the amplitude of TE and TM modes “” and the calculation of the propagation constant “b”.

3) Knowing the components of the following electric field (ox) and (oz) we can determine the electric field component along the axis (oy) from the following relationship:

(13)

(14)

(15)

Which give:

(18)

(19)

(20)

: Is the propagation constant expressed in the spectral domain according to the geometrical sizes and different characteristic elements of the considered area k. It is expressed by the following relationship:

, with (21)

: Wave number in the vacuum.

: Speed of light.

: Indicator mode TE, TM.

: Area considered.

: Relative permittivity of the Area k.

: Permittivity of vacuum [F/m].

: Permeability magnetic of vacuum [H/m].

: Angular pulsation equal to 2Õf [rd/s].

: Admittance of mode returned to the interface W separating the Area 1 and 2, it depends on the dielectric thickness “h₁” and “h₂” of the Area (Figure 2(a)). His expression based on TE and TM modes is:

and (22)

and (23)

We have than we can write:

(24)

4) Calculation of the amplitude of the mode:

Is the amplitude of the mode which will be calculated by applying the following definition:

(25)

m: Index relative to the number of test functions.

When m = 2:

(26)

We put b₁ = 1 and we determine b₂:

(27)

With:: Basic function of the box.

We can write the current form:

(28)

Test functions were chosen as follows:

(29)

With:

On the metal we have:

(30)

(31)

M with a matrix mxm formed of the following elements:

, avec. (32)

The components are unknown and designates a test vector.

The Galerkin method [8] allows us to conclude that Equation (31) admits a solution other than the trivial solution () if:

(33)

From this equation we can determine the propagation constant for each working frequency.

In the expression of the determinant of M we notice the presence of two variables, the propagation constant and the frequency.

(34)

By definition:

(35)

The results of the scalar product in the Equations (32), (34) and (35) are as follows:

;

;

Knowing b₂ we can calculate the amplitude of the mode:

To calculate the via-hole fields we must also calculate the propagation constant b.

2.3.2. Propagation Constant b

The calculation of the electromagnetic field and created by the via-hole is based on the calculation of the propagation constant b.

To calculate the electromagnetic field created by the via-hole with more precise, we must introduce all modes which influence the results. For this we need to calculate the propagation constant b for all modes.

Then to determine the propagation constant b we proceeded as follows: in the expression of the determinant of M we notice the presence of two variables, such as the propagation constant β and the operating frequency f.

First we need to calculate the cut-off frequencies of the study structure, then for a fixed value of the working frequency we need to solve the following equation:

(36)

To trace the curve b depending on the frequency, the resolution of the Equation (36) takes place point by point (Figure 4).

Figure 4 shows the first propagation constant of the six modes of a frequency band that ranges from 0 to 6 GHz. In our work we chose a frequency of 5 GHz, and in that frequency the Figure 4 shows that there are 4 modes present in the structure.

To make sure the Figure 4 is good we compare our work (the fundamental mode) with results calculated by Line Calc software ADS version 11.1.1.

Figure 5 shows the results of the propagation constant b of the fundamental mode are in good agreement with those calculated by the Line Calc software ADS. This validates our calculation method.

Figure 6 shows that the error between our results and those calculated by the ADS software Line calc was 0.2% in the 5 GHz frequency.

Figure 4. Presentation of β in function of the frequency.

Figure 5. Variation of the propagation constant β of the fundamental mode as a function of the frequency.

Figure 6. Error on the results of the propagation constant β the fundamental mode.

2.3.3. Normalization of Electric Field

1) Normalisation of electric field in the Region I:

To calculate the normalized electric field, we must apply the following definition:

(37)

We find:

(38)

with:

2) Normalisation of electric field in the Region II:

We find:

(39)

with:

2.3.4. Convergence of the Via-Hole Field According to the Number of Basic Functions

In our work, the convergence of results is a very important step to achieve the desired accuracy. We see from the above formulas that the electric field created by the via-hole depends on the number of basic functions “n” and the number of test functions “m”.

From Figure 7 we see that the electric field created by the via-hole converges from “n” equal to 150 basic functions.

2.3.5. Convergence of the Via-Hole Field Depending on the Number of Test Function

In this part we have increased the number of test functions for even what value of “m” electrical field converges to a specific value.

When we increase the number of test function we must recalculate the amplitude of mode, the propagation constant b and thereafter the electric field, for each “m” chosen.

From Figure 8 we see that the electric field created by the via-hole converges almost from m = 2.

2.3.6. Magnetic Field Created by the Via-Hole

We express the magnetic field H, created by the via-hole, from the following equation:

(40)

with:

Figure 7. Convergence field created by the via-hole according to the number of basic function.

Figure 8. Field of convergence via-hole according to the number of test function.

By definition the rotational is written:

(41)

This allows us to write:

(42)

In the region “I” of the study structure (Figure 2) the calculated magnetic field along the axis (ox) gives:

(43)

In the region “II” of the structure the magnetic field is written:

(44)

Around “I” the magnetic field along the axis (oy) gives:

(45)

(46)

In the region “II” the magnetic field is:

(47)

(48)

Then the results obtained give the relationship between the magnetic fields and electric fields as follows:

, (49)

,

,

,

2.3.7. The Current J Crossing the Via-Hole

Knowing the magnetic field we can calculate the current crossing the via-hole:

(50)

We also know that:

(51)

It is or then we can write the electric field as follows:

(52)

After that

(53)

The reduced admittance is:

(54)

With: and

And

We prove that

(55)

・ It is

(56)

We put:

(57)

We can write:

・ It is

We put:

(58)

: Reduced current.

Finally we can write:

Knowing the magnetic field we can calculate the current:

is

And also we can write the reduced current in the normalization:

The calculation of the scalar product of the normalization will by applying the formula:

So

and thus

Which β_n depend of the modes TE and TM.

We can write and

So

(59)

The formulation of the current in the region “I”:

(60)

In the region “II” the current written:

(61)

2.3.8. Presentation of the Current and the Field at the Via-Hole

Figures 9-11 for the fundamental mode, the appearance of the current J and E field at the via-hole, without the presence of the microstrip line.

Figure 9. J current appearance at the via-hole for w = 5 mm. (a) in 3D, (b) in 2D for y = 63 pixels.

Figure 10. Appearance of the field E (x, y) at the via-hole for w = 5 mm. (a) in 3D, (b) in 2D for y = 63 pixels.

Figure 11. Appearance of the field E (x, y) at the via-hole for w = 15 mm. (a) in 3D, (b) in 2D for y = 63 pixels.

We note from this Figure 9 that the current is maximum at the via-hole and almost zero else. This clearly verifies the boundary conditions which validates the method of analysis used.

We note from Figure 10 that the field is almost zero on the metal (at the via-hole). To better check the boundary conditions we have increased the width of the via-hole 15 mm (Figure 11). We note that the field is zero on the metal. This clearly verifies the boundary conditions which validate even more the method of analysis used.

3. Convergence of the Iterative Method

The determination of the impedance input of the microstrip line, seen by the excitation source pass by a convergence study.

This Figure 12 shows that the number of iterations required for convergence of results is obtained from 200 iterations for the imaginary part of the impedance input Z_e and from 700 iterations for the real part of impedance input Z_e. So the results obtained below are at the convergence.

The speed of convergence of the iterative method FWCIP is solid compared to other numerical methods used to solve problems of electromagnetism.

4. Validation of the Method

4.1. Influence of Via-Hole on the Circuit Current

The presence of the via-hole in the circuit changes the current waveform in the structure as shown in Figure 13 and Figure 14.

Figure 13 shows that the current is minimum at the end of the line open circuit (without the presence of the via-hole). Figure 14 shows that the current is maximum in the via-hole (the microstrip line connected to the ground through a via-hole).

4.2. Validation of the Results of Different Simulations

Figure 15 presents a comparison of the input impedance of a microstrip line connected to the ground through a via-hole with those calculated by the analytic formula. They show in good agreement. This provides the first validation of the analytical method used.

Figure 16 shows that there is a good agreement between the results “variation of the input impedance according to frequency” of a microstrip line short circuited by a via-hole and microstrip line short-circuited by the box through a metallic ribbon of the same size as the via-hole. This presents the second validation results.

Figure 17 shows a comparison between the input impedance of a line connected to the ground through a via-hole and a line open circuit.

Simulation results clearly show that it is a line short circuit “Z_{e_vh} in the form jZ_c×tg(bL)” and a line open circuit “Z_{e_co} in the form −jZ_c×cotg(bL)”. This validates even more the results of simulations found.

Figure 12. Convergence of the input impedance according to iterations for f = 1.8 GHz.

Figure 13. Current presentation of a microstrip line in open circuit (without the presence of the via-hole).

Figure 14. Current presentation of a microstrip line connected to the ground through a via-hole.

Figure 18 shows a comparison between the input impedance calculated by our method and that calculated by Ansoft HFSS software that is based on the finite element method. The results show that they are in good agreement.

In our work we chose the frequency 5 GHz to calculate the electrical field present in the via-hole and we note the number of mode exists are 4 modes (Figure 4).

Figure 19(a) shows the input impedance Z_e according to the frequency and the number of modes. In this

Figure 15. Comparison Z_e of a microstrip line connected to the ground through a via-hole with those calculated by the analytic formula.

Figure 16. Variation of the input impedance of the microstrip line according to the frequency.

Figure 17. Variation of the input impedance of the microstrip line according to the frequency.

Figure 18. Comparison between our results with those calculated by Ansoft HFSS software.

Figure 19. (a) Variation of the input impedance of the microstrip line according to the frequency; (b) Fluctuations similar to those observed by HFSS.

Figure 19(a) we have presented a comparison between our iterative method while varying the number of mode (fundamental mode, two modes and then four modes).

Based on the various simulations of Z_e, we note that the convergence of our results to those of HFSS is

Figure 20. Resonance of the box.

observed from 4 modes over the entire frequency band used (domain resonance and off-resonance). However it was enough for only two modes to ensure the convergence of our results in the area off-resonance.

Fluctuations observed in the result given by HFSS (Figure 19(a)) is basically caused by the resonance of the box (we even noticed this anomaly as shown in Figure 19(b)).

In fact to justify this we perform the following operation: We took a metal box that contains only a planar source (without the microstrip line and the via-hole).

The different results obtained by simulation, of the input impedance seen by the planar source at the input of the microstrip line (Z_e) show the persistence of the same resonance in the absence of the microstrip line (Figure 20), confirming the presence of a resonance of the box in the structure.

Furthermore, the minimal difference observed between our results and those of HFSS (for the resonant frequency of the box or line) (Figure 19(a) and Figure 19(b)) is mainly due to our initial hypothesis that is to neglect the thickness of the metal strip of the line study, contrary to HFSS which requires a minimum thickness.

5. Conclusion

In this article we have presented an original extension of the iterative method “FWCIP” for the characterization of a planar circuit integrating a via-hole. The inclusion of the via-hole in the circuit has been well defined by writing the new formulation of the iterative process. This formulation is made by the construction of the reflection coefficients that takes into account the presence of the electromagnetic field created by the via-hole in the structure. The results of simulations satisfied the boundary conditions and the continuity of the field throughout the circuit. These results are also in good agreement with those calculated by HFSS software from Ansoft which validates the method of analysis used.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	N’gongo, R.S. (1999) Modélisation des circuits planaires: Application à l’influence du bo?tier. Thèse de Doctorat en Electronique, I.N.P., Toulouse.
[2]	Baudrand, H. and N’gongo, R.S. (1999) Application of Wave Concept Iterative Procedure in Planar Circuits. Recent Research Developments in Microwave Theory and Techniques, 1, 187-197.
[3]	Fethi, M. (2006) Modélisation électromagnétique des structures actives Planaires par une méthode itérative avec sources auxiliaires localisées. Thèse de Doctorat, E.N.I.T., Tunis, Tunisia.
[4]	N’gongo, R.S. and Baudrand, H. (1999) A New Approach for Microstrip Active Antennas Using Modal F.F.T- Algorithm. IEEE Antennas and Propagation Society International Symposium, Orlando, 11-16 July 1999, 1700-1703. http://dx.doi.org/10.1109/aps.1999.788281
[5]	Mejri, F., Aguili, T. and Baudrand, H. (2010) New Formulation of the Iterative Method: Application to a Microwaves Attenuator. Progress in Electromagnetics Research B, 22, 321-340. http://dx.doi.org/10.2528/PIERB10031603
[6]	Garcia, R. (2001) Contribution à l’étude des circuits planaires par une méthode itérative Basée sur le concept d’onde (F.W.C.I.P.). Thèse de Doctorat, I.N.P., Toulouse.
[7]	Aubert, H. and Baudrand, H. (2004) Book “L’électromagnétisme par les schémas équivalents” Première Partie: Les modes dans les structures guidantes et dans les cavités. Cépaduès, Polytechnique France, 37-39.
[8]	Liu, X., Wang, B.-Z. and Lai, S. (2007) Element-Free Galerkin Method in Electromagnetic Scattering Field Computation. Journal of Electromagnetic Waves and Applications, 21, 1915-1923. http://dx.doi.org/10.1163/156939307783152920