On Commutative Δ-Semigroups

Venkata R. S. Kandarpa^*

Giet Engineering College, Rajahmundry, India.

DOI: 10.4236/apm.2016.65021                

Abstract

In this paper entitled on commutative Delta-Semigroups, we have obtained important results on commutative Δ-semigroups.

Keywords

Δ-Semigroup, Commutative Δ-Semigroup, S-Indecomposable Semigroup

Received 18 March 2016; accepted 28 March 2016; published 31 March 2016

Introduction

The concept of a commutative Δ-semigroup was introduced by a Tamura. T in his paper entitled “Commutative semigroup whose lattice of congruences is a chain” appeared in Bulletin de la S. M. F., tome 97 (1969), p. 369 - 380 [1] . A semigroup S is called a Δ-semigroup if and only if the lattice of all congruences on S is a chain with respect to inclusion relation, in fact if S is a Δ-semigroup, then all the ideals of S form a chain, hence all the principal ideals of S from a chain. It is observed that a Δ-semigroup is either an s-indecomposable semigroup or these tunion of two s-indecomposable semigroups. Further every homomorphic image of Δ-semigroup is a Δ- semigroup. A semilattice is a Δ-semigroup if and only if it is of order ≤2, further a Δ-semigroup S is a s-inde- composable semigroups [2] . In fact, if G is a group, then G is an abelian Δ-semigroup if and only if G is a p-quasicyclic for some prime p which is also equivalent for saying that all sub semigroups of G are from a chain [3] . Further an abelian group 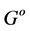with zero is a Δ-semigroup if and only if G is a p-quasicyclic group, p is arbitrary prime. It is also observed that an abelian group 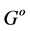with 0 is a Δ-semigroup if G is a p-quasicylicgroup, for an arbitrary prime p. Further in [4] Tamura stated that an ideal of semigroup S, every homomorphism of I onto a non-trivial group G can be extended to a homomorphism of S onto G. we proved that result in theorem 0.8. In fact in this paper, we gave an example to show that the above result need not valid if the word “ideal” is replaced by just “left ideal”. In fact, if a semigroup S contains a proper ideal I and if S is a Δ-semigroup, then neither S nor I is homomorphic onto a non-trivial group.

First, we start with the following preliminaries:

Definition 1 [1] : A semigroup S is called a Δ-semigroup if and only if the lattice of all congruences on S is a chain with respect to inclusion relation. That is, if ρ and σ are congruences on S, then exactly one of the following three holds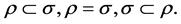

Definition 2 [5] : If I is an ideal of a semigroup S then ρ_I = (I x I) ⋃ 1S is a congruence on S. it is called the Rees-congruence modulo the ideal I.

Definition 3 [4] : A s-indecomposable semigroup is a semigroup which has no semilattice homomorphic image except trivial one (one element semigroup).

Definition 4 [3] : Let p be a prime number. If a group G is the set union of a finite or infinite ascending chain of cyclic groups 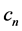of order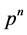, that is,

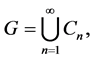
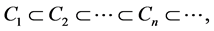
then G is called a p-quasicyclic group, or quacyclic group if it is not necessary to specify p.

Definition 5 [5] : If a semigroup S satisfies the condition the divisibility ordering is a chain, we say then S satisfies the divisibility chain condition.

First, we start with the following Theorem.

Theorem 1: If S is a Δ-semigroup, then all the ideals of S form a chain, hence all the principal ideals of S form a chain.

Proof: If S is a D-semigroup by the definition of D-semigroup; all Rees-congruences on S form a chain. Let ρ and σ be Rees-congruences modulo ideals I and J respectively. Now we show that if and only if.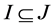

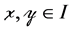Suppose and let so that 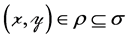and thus 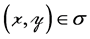and hence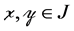. Thus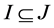. Conversely assume that, let so that both then both an thus and hence. Therefore all the ideals of S form a chain. Since the set of all Rees-congruences of a D-semigroup forma infinite chain which is in fact a complete chain. In this chain every ideal is a principal ideal. Hence all the principal ideals of S form a chain.

Proof: Let A be a D-semigroup that congruences of A form a chain. Let B be a homomorphic image of A, then also in B congruences form a chain. Let be a homomorphism which is onto. Let and be any two congruences on B, then clearly a congruence on A containing the kernel of f. Where is congruence on A. it is observed that. Let Þ and thus (is reflexive) and hence and therefore. Now we observe that is a congruence. We have is reflexive. Let so that and thus (is symmetric) and hence and therefore is symmentric. Let and so that and and thus (is transitive) and hence and therefore is transitive. Thus is an equivalence relation. Let and so that and thus and and hence and (is congruence) and therefore and . Thus is a congruence containing] and is a congruence containing. Now the congruences on A form a chain, thus either or. Suppose that . Now we claim that Let so that and thus and therefore. Thus. Conversely, let so that thus and hence . Thus Hence if and only if. Thus every homomorphic image of a D-semigroup is a D-semigroup.

Theorem 3: A semilattice is a D-semigroup if and only if it is of order £ 2.

Proof: Let L be a semilattice of order £ 2. We define, by for some i.e.

(and and thus). Let a, b be distinct

elements of L and let, , then and are ideals of L. Let and denote the Rees-congruences modulo the ideals and respectively, since,. Suppose L is a Δ-semigroup then either or. Hence either or. For the first case, namely (). There L is a chain. Suppose L is a chain containing at least three elements say Let where is an ideal of L. We defined congruences and on L as follows:

if and only either or,

if and only either or.

Clearly is the Rees-congruence modulo. Now we show that is a Rees-congruences. Clearly is reflexive. Let so that eighter or and hence. Thus is symmetric. Let and so that either or and either or

and thus or and hence then and, let so that either or. Suppose then and and suppose then and and thus Hence and. Thus and. Hence is a congruence modulo. Now but. Suppose, then either or since, so, ,. Suppose then,. Then is contradiction (in L). thus but. Also but not in. Suppose, then either or since, so . Suppose, then . this is contradiction (in L). thus but.

Therefore and. This is contradiction to our assumption. Thus L is a chain of order ≤ 2. Conversely suppose that L is a semilattice with two elements. Then and are congruences on L and clearly Thus all congruences on two elements semilattice are comparable. Thus L is a Δ-semigroup.

Theorem 4: A D-semigroup is either an S-indecomposable semigroup or the set union of two S-indecomposable semigroups.

Proof: We define a relation on S as if and only if that is if and only if if and only if for any filter containing a. Now we show that is an equivalence relation. Let so that thus is reflexive. Let so that and thus if and only if and therefore and hence. Thus is symmetric. Let and so that and and thus if and only if and if and only if and hence if and only if and therefore. Thus. So that is transitive. Thus is an equivalence relation. Now we have to show that is a congruence on S that is so that and. Suppose so that and thus and hence if and only if (since ) if and only if and therefore thus and similarly. Thus is a congruence on S. Now so that and thus if and only if and also since if and only if if only if Thus so that Thus is a semilattice congruence on S. Now we have to show that is the least semilattice congruence on S. If ρ is any semilattice congruence on S. Now we claim that. Suppose so that we have and. Now we have to show that so that. Let K be a filter in S|ρ such that we have by is the natural homomorphic is a filter of s so that. Thus we have for any filter K of S|ρ we have if and only if so that and thus. Thus. Thus is a least semilattice congruence on S. we have is onto homomorphism. Here

We have to show that

Let be the family of completely prime ideals of S such that so for any either or where wherever either or. Here. Suppose then. Now Ι is a completely prime ideal such that and that is is a filter and We have to show that is a filter. Let so that and and thus and hence if then otherwise either or we have so that or so that. This is contradiction, so that. Thus. Hence is a filter. Thus each is a s-indecomposable semigroup.

Now let be a family of completely prime ideals of S. Define by for any we have either or. Let so that either a, or so σ is a reflexive. Let so that either or so that and hence σ is a symmetric. Let and so that either or and either or.

Case (i): Let and, so.

Case (ii): Let and, so and thus or and hence.

Case (iii): Let and so that and thus or and hence a thus.

Thus σ is an equivalence relation on S.

Now we have we have to show that that is or. For any since, so or. Now we take and. So that either or and thus and hence (since). Thus and similarly. Thus σ is a congruence on S. Also clearly (since, so). Now we claim that that is both either or. Now take and so that either or and thus and hence. Thus. Thus σ is a semilattice congruence on S.

Conversely given any semilattice congruence ρ we have to show that we have where s|ρ is a semilattice so that if and only if. Let J be an ideal of s|ρ so that is completely prime ideal. Let so and so that and. Now

So.

Let be the set of all completely prime ideals of the form where J is an ideal of S|ρ. Let σ be the induced semilattice congruence on S. Now if and only if for any completely prime ideals where J is an ideal of S|ρ so that or and thus or and hence. Thus. Now we claim. Let so that. Suppose so that and thus. Then there is an ideal J of S|ρ such that and. Then and. This is contradiction since. Thus and. Then. Hence. Thus. Hence.

Since S is a D-semigroup and every homomorphic image of a D-semigroup is a D-semigroup, So is a D-semigroup, which is also a semilattice D-semigroup if and only if is of order less than 2, so. thus or. If we are through. If then we have where and and

Theorem 5: If G is a group then the following statements are equivalent:

(1) G is an abelian group which is a D-semigroup;

(2) G is a group in which all subgroups from a chain;

(3) For any two elements a and b of a group G, either or for some positive integer n;

(4) G is a p-quasicyclic group for some prime p;

(5) G is a group in which all subsemigroups from a chain.

Proof: (1) Þ (2) Let G be an abelian group such that G is a D-semigroup. Since G be an abelian, so G is a group such that G is a D-semigroup. Let H be any subgroup of G then we have the congruence on H is defined by if and only if. This relation is an equivalence relation. Clearly reflexive, since a is always congruent to a.

It is also symmetric. Since a is congruent to b, so b is also congruent to a. Let and then and. Now we show that if and only if. Now. Now we so that so that . Thus similarly. Thus the relation is congruence. Let then. Hence the set of all subgroups of a group G from a chain.

(2)⟹ (3) Let G be a group satisfying the condition that subgroups from a chain. Then G is periodic and all cyclic subgroups from a chain. i.e. or. If then for some positive integer n, or if. Then for some positive integer n.

(3)⟹ (4) By the periodicity of G it follows that all cyclic subgroups of G form a chain with respect to inclusion. According the order of every element, hence of every cyclic subgroup is a power of a same prime number p. let denote the cyclic subgroup generated by x. Let be the set of all elements of order in G. We have a finite or infinite sequence and

(1)

Let by (3), we have either or for some Assume that so since, so we have similarly, we have Conversely, suppose we have. since so that for some p and for some q and thus (since). Thus and

similarly so that. Thus if and only if are in a same. Choose one element in. then we have a finite or infinite sequence → (2) where and by (1).

If the sequence (2) is finite for some n. that is G cyclic subgroup of order. Thus we have G is a p-quasicyclic group of some prime p.

(4) ⟹ (5) Let G be a p-quasicyclic group, that is G is where is cyclic group of order p. Let H be a subsemigroup of G and let where is the set of all elements of order in G, also. Here

Let by the definition of, If the set is infinite, then. If the set is finite, and if its maximum,. Consequently G has no proper subsemigroup, hence no proper subgroup except in (2). Thus. Thus we have all subsemigroups of G form a chain.

(4) ⇒ (1) Since cyclic groups are abelian, so G is abelian which is a D-semigroup.

(5) ⇒ (1) It follows that G is periodic, therefore every subsemigroup is a subgroup. Hence all subgroups form a chain.

Theorem 6: A group G⁰ with zero is a D-semigroup if and only if the group G is a D-semigroup.

Proof: Let G be a group and G⁰ be the group G with zero element adjoined. Let ρ be any congruence on G. A congruence ρ⁰ on G⁰ is associated with as follows:

if and only if either or,. Clearly ρ⁰ is reflexive, since and ρ is reflexive. Let so that either or and thus or (is symmetric). Thus and hence ρ is symmetric. Let and so that either or and either or and thus or (is transtive). Thus and hence ρ⁰ is transtive. Hence ρ⁰ is an equivalence relation. Let and so that either or an also or (is congruence). Thus and similarly. Thus ρ⁰ is a congruence on G⁰. Clearly the mapping is a one to one. Now we have to show that if and only if. Assume that and let so that either or, and thus either or () and hence. Thus. Conversely suppose that let and thus () and hence () so that. Hence if and only if. Let and denote the universal relation on G and G⁰ respectively. Now we will prove that every congruence on G⁰ is either or ρ⁰, acongruence associated with ρ on G. let be a congruence on G⁰ so that for some and multiflying the both sides by, we have, for all Therefore. Thus every congruence on G⁰ is either or ρ⁰ for some congruence ρ on G, and also clearly. Hence a group G⁰ with zero is a D-semigroup if and only if the group G is a D-semigroup.

Theorem 7: An abelian group G⁰ with zero is a D-semigroup if and only if G is a p-quasicycli group, p is arbitrary prime.

Proof: From theorem 6 we have G is a p-quasicycli group for some prime p if and only if G is an abelian group which is a D-semigroup. From theorem 6 we have a group G⁰ with zero is a D-semigroup if and only if the group Gis a D-semigroup. Since G is an abelian group which is a D-semigroup. So G⁰ is an abelian group with zero is a D-semigroup.

Theorem 8: Let I be an ideal of a semigroup S. If f is a homomorphism of I onto a non-trivial group G, then there is a homomorphism g of S onto G such that f is the restriction of g to I.

Proof: Let is an onto homomorphism defined by if, , If (choose) Now we show that g is a homomorphism.

Case(i): If both,. Thus g is a homomorphism.

Case(ii): If,.

We have and Now since and since and and Thus and hence g is homomorphism.

Case(iii):If,.

We have and. Now we have to show that. Put is onto) so that and thus Then to show that.Now we claim that Put (is onto) so that and hence Then we prove that Now and now we show that i.e. put so that and thus then and hence and therefore Now we have and thus and hence and therefore put Thus Hence g is a homomorphism.

Case(iv):If,.

We have by definition and Now we show that we have and hence and therfore thus Now we show that

We have and thus and hence Thus g is a homomorphism. Since is onto, so that. Now by If then for some. Thus g is onto. Thus is an onto-homomorphism.

Example 1: Let.

Let.

Now.

Where because and since and are positive and also matrix multiplication is associative. Thus S is a semigroup.

Now write.

We verify I is left ideals of S.

Let Thus I is a left ideal.

Now and.

Thus I is not a right ideal.

Now we have () is a group.

Define by.

Now let.

And let.

Thus f is a homomorphism which is also onto.

Now we claim that f can’t be extended to homomorphism such that.

We have is an idempotent.

Since g is a homomorphism, so

Let.

Consider.

An let.

And hence → (1).

Put in (1)

Then.

And hence.

Since, we have.

And therefore.

From (1),.

This is contradiction.

Consider.

So,.

And.

Here. Thus g is not homomorphism.

Theorem 9: If a semigroup S contains a proper ideal I and I and if S is a D-semigroup, then neither S nor I is homomorphic onto a nono-trivial group.

Proof: Suppose there is a homomorphism f of S onto G, so that,. Since G, contains no ideal except G, so Hence. Let ρ be the congruence on S induced by f. For each, there is an element b in I such that. Let σ be the Rees-congruence on S modulo I. Then but then both. Now since but, for some. Since so that both. But if then. Thus and. Which is contradiction to assumption, since S is a D-semigroup. Therefore a S is not homomorphic onto a group G,. Suppose that I is homorphic onto G,. Then by the above theorem there is a homomorphic of onto G. This leads to the same contradiction above. Therefore I is not homomorphic onto G.

NOTES

^*AMS subject classification number 20M10 together with 20M18.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Tamura, T. (1969) Communicative Semigroups Whose Lattices of Congruences Is a Chain. Bulletin de la Société Mathématique de France, 97, 369-380.
[2]	Tamura, T. (1964) Another Proof of a Theorem Concerning the Greatest Semilattice Decomposition of a Semigroup. Proceedings of the Japan Academy, 40, 777-780. http://dx.doi.org/10.3792/pja/1195522562
[3]	Tamura, T. (1956) The Theory of Construction of Finite Semigroups. Osaka Journal of Mathematics, 8, 243-261.
[4]	Tamura, T. (1967) Decomposability of Extension and Its Application to Finite Semigroups. Proceedings of the Japan Academy, 43, 93-97. http://dx.doi.org/10.3792/pja/1195521688
[5]	Howie, J.M. (1969) Fundamentals of Semigroup Theory. Oxford University Press Inc., New York.