Unconditionally Explicit Stable Difference Schemes for Solving Some Linear and Non-Linear Parabolic Differential Equation ()
1. Introduction
A number of difference schemes for solving partial difference equations have been proposed by using the idea of
methods of lines [2] [3] . The scheme is required the condition of step size ratio 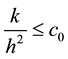 for some constant
for some constant ,
,
where k and h are step sizes for space and time respectively. We [1] [4] -[6] have proposed some explicit scheme and overcome this problem. The problem considered in this paper is linear and nonlinear parabolic problem
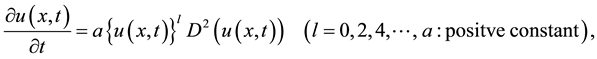 (1.1)
(1.1)
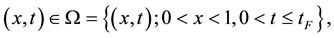
with the initial Dirichlet boundary condition
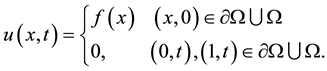 (1.2)
(1.2)
where we set
 (1.3)
(1.3)
We propose the difference approximation to (1.1) where the step size ratio is defined by
 (
( c is any positive constant) (1.4)
c is any positive constant) (1.4)
The outline of this paper is as follows. In §2, by using idea of methods of lines, we present the explicit difference approximation to (1.1). In §3 we study the truncation errors of our scheme. In §4 we study the convergence of the scheme with the condition (1.4) and we will show that our scheme converges to the true solution of (1.1). In §5 we study stability of the scheme, and we will show that our scheme is stable for any step size k and h with the condition (1.4). In §6 we show some numerical examples to justify our methods.
2. Difference Scheme
In the same way as in [1] , we will approximate (1.1) by replacing the derivative for space and time in the difference operator
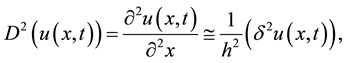
 (2.1)
(2.1)
where  is the central difference operator,
is the central difference operator, 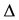 forward difference operator. We denote the approximation to (1.1) at the mesh point
forward difference operator. We denote the approximation to (1.1) at the mesh point 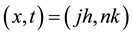
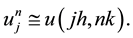
We set
 (2.2)
(2.2)
We define the difference approximation to (1.1) by the following scheme.
If![]() .
.
Then we set
![]() (2.3)
(2.3)
If![]() .
.
Then we set
![]() (2.4)
(2.4)
where
![]() (2.5)
(2.5)
The step size ![]() in (2.3), (2.4) is defined by
in (2.3), (2.4) is defined by
![]() (2.6)
(2.6)
If we set
![]() (2.7)
(2.7)
Then, from (2.3), (2.4), we have
![]() (2.8)
(2.8)
3. Truncation Error
We define the truncation error ![]() of (2.8)
of (2.8)
![]() (3.1)
(3.1)
where, from the definition of (2.7), we have
![]() (3.2)
(3.2)
By Taylor series expansions of the solution ![]() of (1.1), we have
of (1.1), we have
![]() (3.3)
(3.3)
From (3.3), we have
![]() (3.4)
(3.4)
If we set
![]() (3.5)
(3.5)
and
![]() (3.6)
(3.6)
Then, from (3.4), we have the following result.
Theorem 1. The truncation error of the difference approximation (2.8) to (1.1) is given by
![]() (3.7)
(3.7)
where
![]() (3.8)
(3.8)
where ![]() and
and ![]() are defined by (3.5) and (3.6) respectively.
are defined by (3.5) and (3.6) respectively.
4. Convergence
In this section, we study the convergence of the scheme (2.8). We set the approximation error by
![]() (4.1)
(4.1)
We use the abbreviation's
![]()
![]()
![]()
From (2.8), (3.7), (4.1), we have
![]() (4.2)
(4.2)
with
![]() (4.3)
(4.3)
From (2.5), we have
![]() (4.4)
(4.4)
![]() (4.5)
(4.5)
We set the initial conditions of (4.2)
![]() (4.6)
(4.6)
Form (4.2), (4.4), (4.5), (4.6), we have
![]() (4.7)
(4.7)
From (4.7), we have
![]() (4.8)
(4.8)
with
![]() (4.9)
(4.9)
![]() (4.10)
(4.10)
We study the coefficients of (4.8) to![]() .
.
Firstly we consider the case
![]() (4.11)
(4.11)
We set
![]() (4.12)
(4.12)
Then from (4.3), (4.12), we have
![]() (4.13)
(4.13)
![]() (4.14)
(4.14)
We have the equation
![]() (4.15)
(4.15)
![]() (4.16)
(4.16)
From (4.13), (4.14), (4.15), (4.16), we have
![]() (4.17)
(4.17)
If we assume
![]() (4.18)
(4.18)
Then we have
![]() (4.19)
(4.19)
From (3.7), we have
![]() (4.20)
(4.20)
with
![]() (4.21)
(4.21)
From (4.20), we have
![]() (4.22)
(4.22)
where ![]() is defined by (4.21).
is defined by (4.21).
We have from the condition (1.1)
![]() (4.23)
(4.23)
From (4.17), (4.20), (4.23), we have
![]() (4.24)
(4.24)
where ![]() is defined by (4.21) .
is defined by (4.21) .
In the same way to (4.16), from (4.10), we have
![]() (4.25)
(4.25)
From (3.8), we have
![]() (4.26)
(4.26)
After some complicate computation, we have
![]() (4.27)
(4.27)
with
![]()
![]()
![]()
From (4.27), we have
![]() (4.28)
(4.28)
with
![]() (4.29)
(4.29)
From (4.26), we have
![]() (4.30)
(4.30)
with
![]()
![]()
![]()
![]()
From (4.30)
![]() (4.31)
(4.31)
with
![]() (4.32)
(4.32)
From (4.26), (4.28), (4.31), we have
![]() (4.33)
(4.33)
From (4.25), we have
![]() (4.34)
(4.34)
From (4.25), (4.33), (4.34), we have
![]() (4.35)
(4.35)
where ![]() and
and ![]() are defined by (4.29) and (4.32) respectively.
are defined by (4.29) and (4.32) respectively.
From (4.20), we have
![]() (4.36)
(4.36)
where ![]() is defined by (4.21).
is defined by (4.21).
From (4.8), (4.20) (4.24), (4.35), (4.36), we have
![]() (4.37)
(4.37)
where ![]() and
and ![]() are defined by (4.21), (4.29) and (4.32) respectively.
are defined by (4.21), (4.29) and (4.32) respectively.
We set the maximum norm of the function ![]()
![]() (4.38)
(4.38)
Then, from (4.37), we have
![]() (4.39)
(4.39)
From (4.39), we have
![]() (4.40)
(4.40)
Finally we assume
![]() (4.41)
(4.41)
Then, from (4.3), we have
![]() (4.42)
(4.42)
From (4.9), (4.42), we have
![]() (4.43)
(4.43)
In the same way to (4.14), we have
![]() (4.44)
(4.44)
From (3.8), we have after some computation,
![]() (4.45)
(4.45)
with
![]() (4.46)
(4.46)
From (4.8), (4.20), (4.43), (4.44), (4.45), we have
![]() (4.47)
(4.47)
where ![]() and
and ![]() are defined by (4.21) and (4.46) respectively.
are defined by (4.21) and (4.46) respectively.
Then, in the same way to (4.40), from (4.47), we have
![]() (4.48)
(4.48)
We study l = 0. In the almost same way to (4.47), we have
![]() (4.49)
(4.49)
where C1 and C4 are defined by (4.21) and (4.46) with l = 0 respectively.
From (4.49), we have
![]() (4.50)
(4.50)
From (4.40), (4.48), (4.50), we have
Theorem 2. Suppose that for ![]() and
and![]() , there exists positive numbers
, there exists positive numbers ![]() and
and ![]() such that
such that
![]()
If the solution ![]() of (1.1) satisfies conditions (4.18). Then, the approximation
of (1.1) satisfies conditions (4.18). Then, the approximation ![]() generated by the scheme (2.8) converges to the solution
generated by the scheme (2.8) converges to the solution ![]() of the differential Equation (1.1).
of the differential Equation (1.1).
5. Stability
In this section, we study the stability of the numerical process (2.8) and define as follows.
Definition: The numerical processes ![]() is stable if there exists a positive constant
is stable if there exists a positive constant ![]() such that
such that
![]()
where ![]() denotes some norm and the constant
denotes some norm and the constant ![]() is depends on initial value.
is depends on initial value.
We prove that the scheme (2.8) are stable in mean of the von Neumann.
We set
![]()
Then, from (4.7), we have
![]() (5.1)
(5.1)
From (5.1), we have
![]() (5.2)
(5.2)
where ![]() and
and ![]() are defined by (4.9), (4.10) and (3.8) respectively.
are defined by (4.9), (4.10) and (3.8) respectively.
If we assume (4.18) on the solution ![]() of (1.1), Then,in the same way to (4.31), (4.33), (4.45), we have
of (1.1), Then,in the same way to (4.31), (4.33), (4.45), we have
![]() (5.3)
(5.3)
for some constant![]() .
.
From (5.2), (5.3), we have the following result.
Lemma 1. If we assume the solution ![]() of (1.1) satisfies (4.18), Then there exists the constant
of (1.1) satisfies (4.18), Then there exists the constant ![]() such that
such that
![]() (5.4)
(5.4)
with ![]() (5.5)
(5.5)
where ![]() is defined by (5.3). From (2.8), we have
is defined by (5.3). From (2.8), we have
![]() (5.6)
(5.6)
We set the maximum norm of the function ![]()
![]() (5.7)
(5.7)
We have the inequality
![]() (5.8)
(5.8)
From (1.1), we have
![]()
From (5.8), we have
![]() (5.9)
(5.9)
From (2.8), we have
![]() (5.10)
(5.10)
and
![]() (5.11)
(5.11)
From (5.10), (5.11), we have
![]() (5.12)
(5.12)
Firstly we consider
![]()
Then from (5.9) and (5.12), we have
![]() (5.13)
(5.13)
with
![]() (5.14)
(5.14)
where K, ![]() are defined by (4.19) and (5.5) respectively.
are defined by (4.19) and (5.5) respectively.
From (5.14), we have
![]() (5.15)
(5.15)
Lastly, we consider
![]()
From (5.12), we have
![]()
![]() (5.16)
(5.16)
Firstly, we consider the case![]() .
.
Then from (5.16), we have
![]() (5.17)
(5.17)
We have
![]() (5.18)
(5.18)
From (5.10). (5.17), (5.18), we have
![]() (5.19)
(5.19)
with
![]() (5.20)
(5.20)
where K and ![]() are defined by (4.19) and (5.5) respectively.
are defined by (4.19) and (5.5) respectively.
If![]() , Then we set
, Then we set
![]() (5.21)
(5.21)
From (5.21), we have
![]() (5.22)
(5.22)
If![]() , Then we set
, Then we set
![]() (5.23)
(5.23)
From (5.23), we have
![]() (5.24)
(5.24)
From (5.22), (5.24), we set
![]() (5.25)
(5.25)
where ![]() and
and ![]() are satisfy (5.21) and (5.23) respectively.
are satisfy (5.21) and (5.23) respectively.
From (5.6), (5.19) and (5.25), we have
![]()
and we have the following result
![]() (5.26)
(5.26)
From (5.26), we have
![]() (5.27)
(5.27)
where ![]() is defined by (5.25).
is defined by (5.25).
Secondly, in the case![]() , from (5.12), we have
, from (5.12), we have
![]() (5.28)
(5.28)
From (5.28), we have
![]() (5.29)
(5.29)
with
![]() (5.30)
(5.30)
where K and ![]() are defined by (4.19)and (5.5) respectively.
are defined by (4.19)and (5.5) respectively.
In the same way to (5.26), we have
![]() (5.31)
(5.31)
where ![]() is defined by (5.30).
is defined by (5.30).
From (5.15), (5.27), (5.31), we have
Theorem 3.
If the solution ![]() of (1.1) is analytic on the region
of (1.1) is analytic on the region ![]() then the difference approximation (2.8) to (1.1) are stable.
then the difference approximation (2.8) to (1.1) are stable.
6. Numerical Example
Lastly, we study the numerical test in the following non-linear Equation .
![]() (6.1)
(6.1)
and the initial and boundary problem given by,
![]() (6.2)
(6.2)
Applying the difference Equation (2.8) to (6.1) with (6.2), we have the the numerical results in Table 1 and Figure 1, Figure 2.
Table 1. (x = 0/100, 2/100, 20/100, 50/100, 70/100, 98/100), (t = 0, 2/100, 10/100, 20/100, 50/100).
![]()
![]()
Figure 1. Initial data (0 ≤ x ≤ 1, t = 0).
![]()
Figure 2. The numerical solution for 0 ≤ x ≤ 1, t = 50.
As we see in Figure 1, Figure 2, the initial data diffuses slowly. Here the interval [0,1] is divided into
![]() with
with![]() .
.