1. Introduction
While Spirulina was usually consumed naturally, it is now dried and processed in powder, pallets and tablets for nutritional and therapeutic use [1] - [5] . Several strains from different areas are known: platensis, lonar, paracas, maxima pacifica. All these species are distinguished by their morphology (more or less constricted turns, wavy, straight etc...) and develop over a clayey basis and a black sludge resulting from anaerobic fermentation of dead algae [6] . World production of Spirulina is continuously growing while several semi-industrial and industrial Spirulina farms are developing. According to [7] , the production of dry Spirulina was about 5000 tons in 2012. To have a rational resources management and a regular production, drying processes must be accurately controlled. The drying stage aims to reduce its mass and volume, ensure equilibrium moisture content, avoid the development of micro-organisms, and increase its mechanical strength to support the shocks of handling operation. The convective drying is one of the most used technologies to preserve Spirulina. Whatever the production level, the drying is a crucial step which directly influences the quality of the final product. Nevertheless, drying is usually considered as being the stage that exposes the product to secondary risks, which can be classified into two groups:
physical phenomena: heterogeneous distribution of moisture, watertight barrier when “crust” appears in surface, cracks and deformation, degradation of texture, reduction of density and rehydration capacity, change in gustative characteristics, migration or retention of volatile constituents, degradation of colour, nutrients and flavour [1] [3] [8] ;
biochemical reactions: oxidation of vitamins and fat, denaturation of proteins, enzymatic reactions [9] .
The transition from traditional to industrial processes calls for optimization approaches based on laboratory experimental investigation and numerical modelling development.
Regarding the modelling of drying processes of Spirulina, little work has been done so far. Pioneered experimental analysis carried out by [10] - [12] allowed the identification of some drying phases and the influence of operating conditions such as air velocity, temperature and humidity. The sorption behaviour has been characterized by using different methods (Dynamic Vapor Soption, gravimetric method). By taking into account the solid phase shrinkage, Hernandez [13] led to the identification of a drying phase at constant velocity. The evolutions of porosity and density during drying experiments were determined by kinetic analysis [8] [14] . In the literature, the water transport coefficients of some food products such as the papaya [15] , beef meat [16] , coffee [17] [18] and Okra [19] were determined by analytical models [20] [21] . Crank (1975) [22] focused on very simplifying assumptions which mask the contribution of certain parameters at water transport, particularly the shrinkage of the solid structure and the heterogeneity of the water content. In addition, this model is commonly used for low water contents. The diffusion coefficient of Spirulina was estimated by [23] for water contents of less than w = 2 kgw/kgdm by applying the Crank’s approach and considering two areas where the water content is not necessarily homogeneous.
This study aims at optimizing the conservation of the product and characterizing the water transport mechanisms during isothermal drying of Spirulina. The main issues to be addressed are:
establishing the desorption isotherm at two temperatures,
analysing the internal mechanism of water transport,
assessment of water transport coefficient as a function of water content.
With these objectives, a specific experimental method and the associated identification procedure have been developed to take into account the shrinkage of the solid matrix observed during drying.
2. Materials and Method
The Spirulina samples used in this study are platens is type and come from two farms located in two different areas:
“Loumbila” farm situated at 15 km in the north of Ouagadougou, Burkina Faso. This material sample will be named B-sample,
“La Fon del Cardaire” farm situated at Gignac in the south of France. This material will be named F-sample.
Their production mode is no different from one farm to another, from one country to another. Microscopic observation shows that Spirulina platensis is in spiral form with much tighter turns than those of other kind [24] . In both farms, harvested Spirulina is drained and rinsed through a 20 µm filter. Using standard methods, apparent and real densities of water and solid phases have been measured and the main characteristics are summarized in Table 1.
![]()
Table 1. Characteristics of fresh material (initial conditions).
2.1. Sample Preparation
For the experimental study, the fresh pulp is moulded into cylindrical samples. To avoid variability and ensure identical initial conditions between samples, the following design process has been adopted:
The fresh biomass is moulded in a cylindrical device of 20 mm diameter and 40 mm length composed of a tube and a piston made in Teflon;
The cylindrical surface of samples is wrapped with plastic film to prevent adhesion between samples. Both end faces are free to ensure a one-dimensional water transport along sample axis;
A sample is kept if its initial mass is
.
From the initial mass and dry mass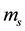
, the initial water content of each sample was determined by the following Equation (1). Even if the initial water contents of materials are different (2.73 for B-sample and 3.12 for F-sample), one can note that the apparent density 
is nearly identical for both.
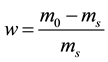(1)
2.2. Desorption Isotherm
Desorption isotherm of Spirulina platensis was determined by the gravimetric method. Its principle consists in arranging samples above saturated salt solutions which regulate the relative humidity of the surrounding atmosphere at constant temperature. The experimental device relies on 9 glass desiccators containing different saturated salt solutions to cover the whole range of relative humidity [25] : KOH, LiCl, KCH3CO2, MgCl2, K2CO3, Mg(NO3)2, NaNO2, NaCl, KCl. The desiccators are placed in a thermo-regulated chamber (Memmert UFP 600). At given times, weighings are performed using a high precision scale 10−4 g, until the variation of mass between two successive measurements becomes negligible. At equilibrium, samples are dehydrated in an oven at 70˚C for 48 hours to determine their dry mass. The equilibrium mass water content of the product is calculated by:
(2)
To describe the complete desorption isotherm curve, the GAB model [26] if written:
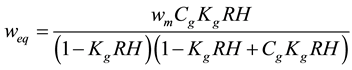(3)
where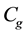 
is the constant of Guggenheim, 
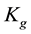the correction factor of the model and wm is the monolayer water content. This description has shown to be suitable for various agro-products of the same kind [27] - [30] .
2.3. Drying Kinetics
A cylindrical sample is hanged from a force sensor (LSB200 “Andilog”, 0.1% accuracy) inside a closed desiccator where the relative humidity is regulated at RH = 6% by a potassium hydroxide KOH solution. The desiccator is placed in a thermo-regulated chamber (Memmert UFP600) where the temperature is maintained at 50˚C. The mass of sample is recorded continuously during the drying process allowing to draw the drying kinetics.
2.4. Characterization of Transport Coefficient
The water transport phenomenon is considered to be governed by the first Fick’s law, which relates the water mass flux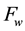 
to the gradient of apparent density 
through a phenomenological transport coefficient 
[31] . It is written [32] - [34] :
(4)
The transport coefficient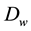 
depends on the fluid and the material through which the transport process develops. The various steps required to experimentally characterize this coefficient are described below.
2.4.1. Experimental Device and Procedure
The experimental setup is constituted of a desiccator where the relative humidity is regulated at RH = 6% by a potassium hydroxide KOH solution (Figure 1). The cylindrical samples (Figure 1(a)) are put above the solution (Figure 1(b)) while the desiccator is placed in a thermo-regulated chamber (Memmert UFP 600) where the temperature is maintained at 50˚C.
At specific time steps of the drying process, one of the samples is removed from the desiccator and immediately introduced in a cutting device to obtain slices of 2 mm thickness (Figure 1(c)) perpendicular to the axis ox. The mass water content of each slice 
is determined by differential weighing after 48 hours drying at 70˚C for complete dehydration. Since samples and boundary conditions are symmetrical, the averaged water content of symmetrical points is considered. This methodology allows accessing to water content profiles ![]()
at different stages during the drying process (Figure 1(d)). As it aims to characterize the water transport phenomena in a unique sample from measurements obtained on various samples, it is essential to have the same initial conditions in all samples. Indeed, even if a particular attention is paid to the preparation of samples, this methodology can introduce some discrepancies. Eventually, experimental water content profiles are approximated by simple polynomial Equations (5) introducing 3 parameters a, b and c at each time step:
![]()
(5)
This expression ensures to have a symmetrical evolution with a no flux condition at the symmetry plane. Experiments are carried out at 50˚C during 120 hours. It appears that for longer time period, the material starts to denature and the development of micro-organisms are observed. This would modify water transport processes and must be avoided. For lower temperature, the drying process is too slow to reach low water content values and the range of water content investigated is too narrow.
![]()
Figure 1. Principe of the experimental setup for the characterization of water transport coefficient in Spirulina samples.
2.4.2. Theoretical Modelling
Simplifying assumptions are considered to develop the descriptive equations of water transport:
the material is assumed to remain diphasic along the experiment,
the initial water content in the product is homogeneous,
both solid and liquid phases are incompressible,
water transport is one-dimensional along the cylindrical sample axis x.
The real mass densities are determined over intrinsic volume of water and solid phases:
![]()
(6)
While the apparent mass densities are defined over the sample volume V:
![]()
(7)
The material being biphasic, the apparent densities can be expressed [35] as:
![]()
(8)
![]()
(9)
where ![]()
is the ratio of real densities. Considering ![]()
and ![]()
as the water and solid phase velocities along x, mass balance equations are written [36] [37]
![]()
(10)
![]()
(11)
The relative water mass flux with respect to solid phase is written as:
![]()
(12)
From symmetry considerations,![]()
. Thus mass balance Equations (10) and (11) can be integrated to obtain:
![]()
(13)
![]()
(14)
Replacing these expressions in Equation (12) leads to:
![]()
(15)
Considering Equations (8) and (9), the relative water flux becomes:
![]()
(16)
By relying on the expression of apparent density (8), the gradient of water density introduced in Equation (4) is written:
![]()
(17)
In the case of geometry and boundary conditions used in experiments, radial water transport can be neglected so that water content is considered uniform in a cross-section at abscissa x. The main advantage provided by the fitting of water content profiles through a simple polynomial Equation (5) is that it can be inverted, derivated and integrated analytically. From Equation (4), Equation 16) and Equation (17), the transport coefficient ![]()
can be evaluated at various abscissa x and the methodology is developed in next section.
2.4.3. Assessment of Transport Coefficient
For a particular time step tj and a given water content![]()
, the fitting of the associated water content profile (Equation (5)) can be inverted to give the corresponding abscissa![]()
. Knowing this abscissa, the values of the water flux ![]()
(Equation (16)) and the gradient of water density ![]()
(Equation (17)) can be computed directly.
Actually, in Figure 1(d), the horizontal line associated with the given water content ![]()
can intersect several water content profiles providing a set of values ![]()
leading to a set of couples![]()
. This
set of couples is associated to a single value of the water content ![]()
and must correspond to a unique value of the transport coefficient![]()
. Therefore, the calculation, in this way, by scrolling over a range of water content values between of the transport coefficient from Fick’s law (Equation (4)) amounts to determine the slope of the
linear relation associated with the set of couples![]()
. In this way, by scrolling over a range of water content values between![]()
, this method allows to determine the evolution of the transport coefficient ![]()
as a function of water content.
Furthermore, the accuracy in the determination of experimental results is estimated the statistical parameters: the coefficient ![]()
and the root mean square error (RMSE). These parameters were expressed according to the following equations [38] - [40] :
![]()
(18)
![]()
(19)
3. Results and Discussion
3.1. Desorption Isotherm
Desorption isotherm curves for both samples at 25˚C and 50˚C are represented in Figure 2. Theoretical modelling based on GAB description (Equation (3)) is also drawn while fitting parameters are given Table 2. The overall shape of curves is identical to those obtained by [11] with Spirulina platensis. The variation of desorption isotherm between 25˚C and 50˚C is similar to the one underlined with various food products such as banana, apple, coffee and pasta [18] [41] - [43] . It is noteworthy that the sorption behaviour is not sensitive to the geographical origin, i.e., both samples cultivated in different areas lead to nearly identical measures.
According to industrial standards, the water content of Spirulina should not exceed 0.075 [44] . From Figure 2, this corresponds to a maximum relative humidity in storage atmosphere of RH = 28% at 25˚C and RH = 52% at 50˚C.
3.2. Water Content Profiles
The destructive method presented above allowed us to obtain a representative evolution of the distribution of water inside Spirulina platensis samples (Figure 3 and Figure 4). These profiles are accurately approximated by a simple polynomial Equations (5). Water content profiles evidence that drying process starts from free ends and penetrates slowly inside samples. Distribution of water being heterogeneous (Figure 3 and Figure 4), water loss by evaporation at the exchange surface are not completely compensated by internal transport. A significant shrinkage of the solid matrix is observed as the length of samples decreases from 20 mm to 16.4 mm. This
![]()
Figure 2. Desorption isotherm curves of Spirulina platensis at 25˚C and 50˚C.
![]()
Figure 3. Water content profiles in B-sample at 50˚C.
![]()
Figure 4. Water content profiles in F-sample at 50˚C.
![]()
Table 2. Isotherm modeling parameter values.
shrinkage causes strong concentration gradients in external parts. Similar trends have already been highlighted for highly deformable materials such as rubber [45] or Agar gel [46] .
The fact that, during experiments, water content profiles remain almost at in the central part of samples means that transport coefficient is lower in both ends than in central part. The shrinkage of the solid matrix causes a significant decrease of water transport that can lead in some cases to a “croutage” of external surfaces.
3.3. Kinetics
The drying kinetic obtained from continuous measurement is presented in Figure 5. The average water content values calculated from water content profiles have been added for comparison. The good agreement observed between both drying kinetics highlights that the destructive cutting method doesn’t cause perturbation of the profiles and that the influence of external conditions is negligible. So, we can consider that the water content profiles (Figure 3 and Figure 4) determined from different samples are representative of the evolution of a single sample.
3.4. Water Transport Coefficient
From the water content profiles presented above, the range of water content that can be fairly investigated is![]()
, i.e., an horizontal line intersects at least two water content profiles. In this range of water content, the water flux ![]()
and the gradient of water density ![]()
can be determined by applying the computational procedure described in previous section. Both quantities are represented in Figure 6 and Figure 7 for regularly distributed values of water content. For each water content value, a fairly linear correlation is observed between water flux and density gradient. Therefore, the water transport coefficient is determined from the slope of each linear approximation.
For both Spirulina materials (B and F), the dependences of water transport coefficients with respect to the water content are shown in Figure 8. As already noticed with desorption isotherm curves, experimental results are similar whatever the geographical origin of Spirulina material, Burkina-Faso or France. Therefore, it is considered that both experiments are representative of a single water transport coefficient evolution. Experimental points are accurately described by the following exponential expression:
![]()
(20)
Non-linear regression procedure yielded a good correlation between experimental and theoretical data with a correlation coefficient ![]()
and a standard deviation![]()
. This figure evidences the monotonic dependence of water transport coefficient with regard to the water content with an exponential variation. One can note a sharp increase of the transport coefficient above a water content of w = 2. This tendency has already been observed with rubber [45] , Agar gel [47] , clay [48] , coffee [18] and wood [31] . This variation is attributed to the contraction of the porous microstructure and the reduction of pore size distribution that lead to a decrease of water permeability. In the case of Spirulina, the [5] has shown that the critical water content beyond which the shrinkage slow down water transport mechanism was of the order of w = 1.82.
Furthermore, previous results [45] [47] highlighted an increase of water transport coefficient for low values of water content. This would result from the stiffening of the porous skeleton and the development of wider pores. This matrix stiffening is generally concomitant with the penetration of the gas phase inside material. At this stage, drying phenomena shift from biphasic to triphasic regime and water transport mechanisms recall more elaborated modelling. This issue is beyond the scope of this paper. The transport coefficients measured in previous works are compared to those of the present study in Table 3.
![]()
Figure 5. Comparison of drying kinetics at 50˚C.
![]()
Figure 6. Water mass flux ![]()
as a function of the gradient of water apparent density ![]()
in B-sample at 50˚C.
![]()
Figure 7. Water mass flux ![]()
as a function of the gradient of water apparent density ![]()
in F-sample at 50˚C.
![]()
Figure 8. Water transport coefficient ![]()
as a function of water content at 50˚C.
![]()
Table 3. Comparison of values of the transport coefficient studied than those obtained by other authors.
We find that for water contents of the order of w = 3, the values obtained by the Crank method [12] with a velocity of the imposed air are lower than those given by cutting approach. The high values of the present study may be due to the taking into account of the solid shrinkage which contributes to push the water whereas in the case of the method Crank, it is assumed constant. The results are in agreement for low water contents where the shrinkage becomes negligible ( [23] , present study). This study allows us to understand the shrinkage contribution to the variation of the transport coefficient of Spirulina platensis on a large range of water content.
4. Conclusions
Fresh material of Spirulina platensis has been experimentally characterized including desorption isotherm curves at 25˚C and 50˚C, drying kinetics and water transport phenomena. Concerning water transport, a methodology is proposed to determine the water content profiles inside a Spirulina sample during the drying process. Theses profiles are then introduced in a theoretical modelling accounting for matrix shrinkage and relative water flux leading to identifying the dependence of water transport coefficient with respect to water content. Compared to standard methods based on Crank diffusion equation that give an overall and constant value, this approach allows a more precise analysis of water transport mechanism and a local measure of transport coefficient.
While two different fresh materials have been characterized, one cultivated in Burkina-Faso and another one in France, the results highlighted that sorption behaviour and water transport properties are almost identical whatever the geographical origin. Water transport coefficient evidences an exponential dependence on water content which is in agreement with previous works carried out on various food products. Ongoing works will allow defining the transition between biphasic and triphasic drying regimes and investigating the influence of gas phase on water transport. This work would help to improve numerical simulation of water transport inside fresh material in order to optimize industrial drying processes.
Acknowledgements
The authors are grateful to:
Institut International d’Ingénierie de l’Eau et de l’Environnement and PIMASO for financial support which allowed the realization of this work,
Fédération Française des Spiruliniers for the supply of Spirulina fresh product.
Nomenclature
NOTES
*Corresponding author.