A Game-Theoretic Model for Bystanders’ Behaviour in Classes with Bullying ()
1. Introduction
According to a survey on problematic behaviours by the Ministry of Education, Culture, Sports, Science and Technology (MEXT) in Japan, the number of recognized incidents of bullying at all grade levels nationwide in 2012 was 198,108, 2.82 times than that of the previous year. This represents the largest number of recorded incidents since the survey began [1]. Additionally, there were 196 student suicides in 2012, of which 3.1% were understood to have resulted from bullying; this made the issue of bullying a serious social problem that must be solved.
Morita [2] emphasised the importance of bystanders’ behaviour. Shibata et al. [3] conducted an economic analysis on the behaviour of bystanders. Glass and Smith [4] established that a reduced class size can be expected to produce academic achievement. Additionally, Smith and Glass [5] have shown that small class size is effective in improving student attitudes and behaviour.
This paper comprises several sections in which different aspects of bullying analyses are discussed. Section 2 explains our model in detail. Section 3 analyses the Nash equilibrium within the model. Section 4 discusses numerical experiments with changes to class size and the impact of these changes on behaviour. Section 5 summarizes our results.
2. A Game-Theoretic Model for Bullying
There are three kinds of people in this situation: the bully, the bullied child and bystanders. In this paper we only focus on bystanders’ behaviour in a class where there is bullying. Suppose that there are  bystanders in the class each bystander can take behaviour R, where a student reports bullying to a teacher, or behaviour S, where a student does not report the bullying. Bullying is resolved when more than
bystanders in the class each bystander can take behaviour R, where a student reports bullying to a teacher, or behaviour S, where a student does not report the bullying. Bullying is resolved when more than 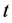 students report the bullying. All players are initially granted a utility level
students report the bullying. All players are initially granted a utility level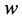 . When bullying occurs, players incur a negative externality (disutility)
. When bullying occurs, players incur a negative externality (disutility)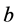 . Cost
. Cost 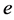 is constantly incurred for student who selects behaviour R, regardless of whether bullying is stopped or not.
is constantly incurred for student who selects behaviour R, regardless of whether bullying is stopped or not.
Then, a non-cooperative n-person game model [6] [7] is formulated, shown in Table 1 . Each value shows the player’s gain in each case, where X denotes the number of reporters other than himself of herself.
3. Nash Equilibrium in the Bullying Model
Each bystander play this game according to Table 1 . Suppose each bystander has the same probability of reporting, q. When players other than oneself select behaviour R with a probability q, the probability of case 1, 2 and 3 are 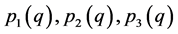 respectively as shown below:
respectively as shown below:
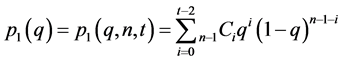 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
The Expected utility of 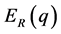 when a player selecting behaviour R, and the Expected utility of
when a player selecting behaviour R, and the Expected utility of 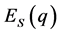 when a player selecting behaviour S are expressed with the following equations.
when a player selecting behaviour S are expressed with the following equations.
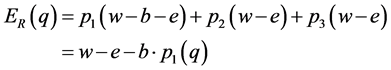 (5)
(5)
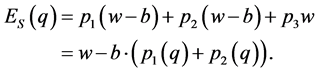 (6)
(6)
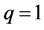 is the state when all players select behaviour R and
is the state when all players select behaviour R and  is the state when all players select behaviour S. When
is the state when all players select behaviour S. When , the result is as
, the result is as![]() .
.
From Equation (2), we have![]() ,
, ![]() and
and
![]() (7)
(7)
It follows that
![]() (8)
(8)
where![]() .
.
Figure 1 shows that there are two values of which hold ![]() when
when![]() . Let them denote
. Let them denote![]() ,
,![]() .
.
Figure 2 shows the relationship between Expected utilities ![]() and
and ![]() and for player behaviours R and S where
and for player behaviours R and S where![]() .
.
As we saw in Figure 2, ![]() and
and ![]() have two intersections for the range
have two intersections for the range![]() ,
, ![]() occurs. This indicates that a free rider phenomenon occurs where many other players report bullying, but the player in question decides it is better not to report. Based on the above, we can make the following proposition.
occurs. This indicates that a free rider phenomenon occurs where many other players report bullying, but the player in question decides it is better not to report. Based on the above, we can make the following proposition.
![]()
Table 1. Changes to player gain by the number of reporters when selecting either behaviour R or S.
![]()
Figure 2. Expected utility when there are two intersections of ![]() and
and![]() .
.
Proposition 1
1) A pure strategy Nash equilibrium always exists in which no player reports bullying. Only when ![]() is true, two mixed strategies Nash equilibrium exists.
is true, two mixed strategies Nash equilibrium exists.
2) When![]() , segment
, segment ![]() exists for q where
exists for q where![]() . Conversely, when
. Conversely, when
![]() it is always true.
it is always true.
When examining Figure 1, we see that we can expand the range ![]() of
of ![]() by reducing
by reducing![]() , since
, since ![]() is decreased and
is decreased and ![]() is increased. Based on the above, we can make the following propositions.
is increased. Based on the above, we can make the following propositions.
Proposition 2
An increase in b or a decrease in ![]() due to a decrease in e causes a decrease in
due to a decrease in e causes a decrease in ![]() and an increase in
and an increase in![]() .
.
By differentiating both sides of ![]() results in
results in![]() . Because
. Because ![]() satisfies
satisfies
![]() and
and ![]() satisfies
satisfies![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() are solved in similar fa-
are solved in similar fa-
shion.
4. Behavior Resulting from Changing the Number of Bystanders in the Class
Let us examine changes in ![]() and
and ![]() that occur at the two intersections with
that occur at the two intersections with ![]() and
and ![]() when changing only
when changing only![]() , the number of bystanders in the class, while the ratio of threshold to the number of bystanders is kept constant at
, the number of bystanders in the class, while the ratio of threshold to the number of bystanders is kept constant at![]() . Figure 3 is a graph of
. Figure 3 is a graph of ![]() where the number of
where the number of ![]() is changing. As the value of
is changing. As the value of ![]() becomes smaller,
becomes smaller, ![]() becomes smaller and
becomes smaller and ![]() becomes larger. Thus, the range
becomes larger. Thus, the range ![]() of
of ![]() expands.
expands.
Figure 4 is a graph that shows the value of ![]() and
and ![]() for four cases, (n, t) = (20, 10), (40, 20)…, where the ratio of
for four cases, (n, t) = (20, 10), (40, 20)…, where the ratio of ![]() keeps a constant
keeps a constant![]() . As
. As ![]() becomes smaller,
becomes smaller, ![]() becomes smaller and
becomes smaller and ![]() becomes larger. Again, the range
becomes larger. Again, the range ![]() of
of ![]() expands. On the other hand, as class size
expands. On the other hand, as class size ![]() becomes larger,
becomes larger, ![]() becomes larger and
becomes larger and ![]() becomes smaller. The values of the upper limit
becomes smaller. The values of the upper limit ![]() decrease, and the lower limit
decrease, and the lower limit ![]() increase, and the range
increase, and the range ![]() of
of ![]() shrinks.
shrinks.
Proposition 3.
1) For![]() , the following relations hold.
, the following relations hold.
![]() (9)
(9)
2) For i such as ![]() we have the following in equations.
we have the following in equations.
![]() ,
,
![]() . (10)
. (10)
![]()
Figure 3. A graph of ![]() when increasing n and t while maintaining
when increasing n and t while maintaining![]() .
.
Since
![]() (11)
(11)
where ![]() (12)
(12)
using the relation ![]() (13)
(13)
it is left for us to prove ![]() (14)
(14)
![]() can be written as
can be written as
![]() (15)
(15)
From relations
![]() (16)
(16)
we obtain![]() , then the proof is completed.
, then the proof is completed.
Proposition 3 (2) shows that adopting smaller class sizes is effective for reducing bullying. It gives the effectiveness of small-group education.
5. Conclusion
In this paper we modelled the behaviour of bystanders of students in a non-cooperative n-player game. We showed by making![]() , the ratio of a threshold number of reporters to the number of bystanders, constant and decreasing
, the ratio of a threshold number of reporters to the number of bystanders, constant and decreasing ![]() becomes possible to decrease the lower limit
becomes possible to decrease the lower limit ![]() and to increase the upper limit
and to increase the upper limit ![]() of the probability of reporting bullying. If class sizes are smaller, the number of bystanders should be fewer. This shows the possibility of eliminating bullying by using the smaller number of bystanders. Note that the reason we insist that smaller classes are better, not because it is easier for a teacher to manage smaller classes. More intuitively, Proposition 3 shows that bystanders can report bullying more easily if they are in a smaller class.
of the probability of reporting bullying. If class sizes are smaller, the number of bystanders should be fewer. This shows the possibility of eliminating bullying by using the smaller number of bystanders. Note that the reason we insist that smaller classes are better, not because it is easier for a teacher to manage smaller classes. More intuitively, Proposition 3 shows that bystanders can report bullying more easily if they are in a smaller class.
Furthermore, to expand the range ![]() of
of![]() , it is useful to raise the disutility
, it is useful to raise the disutility ![]() associated with continued bullying and to reduce the cost e of reporting on bullies.
associated with continued bullying and to reduce the cost e of reporting on bullies.
Finally, this study has demonstrated the existence of the “free riding” phenomenon: if the majority of other people report, it is advantageous for any given person not to do so.
Acknowledgements
This work was supported by JSPS KAKENHI Grant Numbers 25350468.