1. Introduction
Circulant matrix plays an important role in the matrix theory, its special structure and properties have been widely used in applied mathematics, physics, modern engineering, and so on [1] -[6] . There have been many new circulant matrices come fordward [7] -[12] . In this paper we will firstly put forward the concept of the FLDcircr matrix and the basic FLDcircr matrix. The sum, the difference, the product, the inverse and the adjoint matrix of this type of matrices are still FLDcircr matrices. Then, we will give five discriminance for FLDcircr matrix by constructing the basic FLDcircr matrix. At last, we will discuss the fast algorithm of the inverse and generalized inverse of the FLDcircr matrix and give the numerical example. In this paper, we just study the square matrices in complex field.
2. Definition of the FLDcircr Matrix
Definition 2.1 For a square matrix A of order n, if its form is
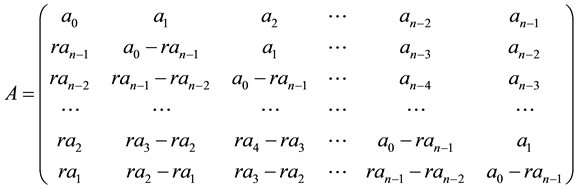 ,
,
We call it the FLDcircr matrix, and denote shortly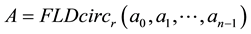 .
.
Definition 2.2 Let D is the basic FLDcircr matrix of order n, that is
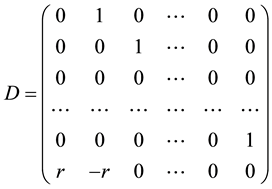 .
.
We obtain 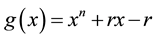 is the characteristic polynomial of D,
is the characteristic polynomial of D, 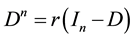 , we specify
, we specify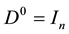 .
.
From the definition of FLDcircr matrix, we can prove the following proposition.
Proposition 2.3 If A and B are FLDcircr matrices, then A + B, A − B and kA are both FLDcircr matrices, for any k belongs to the complex field.
Definition 2.4 Let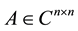 ,the index of A is the least nonnegative integer k such that
,the index of A is the least nonnegative integer k such that , we note it as
, we note it as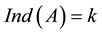 . If A is nonsingular, then
. If A is nonsingular, then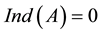 ; if A is singular, then
; if A is singular, then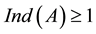 .
.
Definition 2.5 Let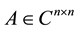 , if there is
, if there is 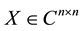 which satisfies
which satisfies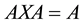 ,
, 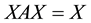 at the same time, we named X as the reflexive generalize inverse of A, we note it as
at the same time, we named X as the reflexive generalize inverse of A, we note it as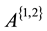 .
.
Definition 2.6 Let![]() ,
, ![]() , if
, if ![]() satisfies
satisfies
![]()
Then we denote X as the Drazin inverse of A, note it as![]() .
.
Lemma 2.7 If polynomial matrix ![]() can transformed into
can transformed into ![]() after elemen-
after elemen-
tary row transformation, then we have![]() , and
, and![]() .
.
3. The Discriminance of the FLDcircr Matrix
Theorem 3.1 A is an FLDcircr matrix if and only if A is of the following form
![]() (1)
(1)
For some polynomial![]() .
.
Proof. By the Definition 2.1 and Definition 2.2, we get this result.
Theorem 3.2 A is an FLDcircr matrix if and only if AD = DA, D is the basic FLDcircr matrix.
Proof. ![]() For A is an FLDcircr matrix, from the definition of A and D, we obtain
For A is an FLDcircr matrix, from the definition of A and D, we obtain ![]()
![]() By the method of undetermined coefficients, let
By the method of undetermined coefficients, let
![]() .
.
Due to
![]()
It follows that
![]()
We obtain
![]() ,
,
So A is an FLDcircr matrix.
Corollary 3.3 If A and B are both FLDcircr matrices, then AB and BA are FLDcircr matrices. Furthermore, we get AB = BA.
Proof. Since A and B are FLDcircr matrices, by the Theorem 3.2, we get
![]()
Hence
![]()
Then, AB and BA are both FLDcircr matrices.
From Theorem 3.1, we have
![]()
4. The Diagonalization of the FLDcircr Matrix
First, we consider the diagonalization of the basic FLDcircr matrix D.
For the characteristic polynomial ![]() of D has n different roots. So, D has n different eigenvalues:
of D has n different roots. So, D has n different eigenvalues:
![]() .
.
Let
![]() ,
,
Obviously, ![]() is a nonsingular Vandermonde matrix about
is a nonsingular Vandermonde matrix about![]() , and
, and
![]() . (2)
. (2)
Next, we study the diagonalization of general FLDcircr matrix A.
From Theorem 3.1 and Equation (2), we obtain
![]()
The eigenvalues of A are
![]() .
.
Theorem 4.1 A is an FLDcircr matrix if and only if ![]() is a diagonal matrix.
is a diagonal matrix.
Proof. ![]() If A is an FLDcircr matrix, from the above discussion, we have
If A is an FLDcircr matrix, from the above discussion, we have
![]() .
.
![]() Let
Let![]() ,
, ![]() is a diagonal matrix, then
is a diagonal matrix, then
![]() .
.
Let![]() , from Equation (2) we have
, from Equation (2) we have
![]() ,
,
Thus
![]()
For ![]() and
and ![]() are both diagonal matrix, so
are both diagonal matrix, so
![]()
hence, A is an FLDcircr matrix.
Theorem 4.2 A is a nonsingular FLDcircr matrix if and only if the eigenvalues![]() , where
, where ![]() are eigenvalues of the basic FLDcircr matrix.
are eigenvalues of the basic FLDcircr matrix.
Proof. ![]() For A is a nonsingular FLDcircr matrix, from the above discussion, we have
For A is a nonsingular FLDcircr matrix, from the above discussion, we have
![]() ,
,
where ![]() are eigenvalues of A.
are eigenvalues of A.
So
![]() .
.
Hence, if A is a nonsingular FLDcircr matrix, we have![]() .
.
![]() Due to,
Due to,
Then
![]() ,
,
So A is nonsingular.
5. The Fast Algorithm of the Inverse and Generalized Inverse of the FLDcircr Matrix
Theorem 5.1 If A is a nonsingular matrix, then A is an FLDcircr matrix if and only if ![]() is an FLDcircr matrix.
is an FLDcircr matrix.
Proof. ![]() From A is nonsingular and Theorem 3.2, we obtain
From A is nonsingular and Theorem 3.2, we obtain
![]()
Hence
![]()
That is to say ![]() is an FLDcircr matrix.
is an FLDcircr matrix.
![]() Clearly, the nonsingular matrix A is an FLDcircr matrix.
Clearly, the nonsingular matrix A is an FLDcircr matrix.
Corollary 5.2 If A is a nonsingular FLDcircr matrix, then ![]() is a nonsingular FLDcircr matrix.
is a nonsingular FLDcircr matrix.
Proof. For A is an FLDcircr matrix, we have![]() , so
, so
![]() .
.
Due to
![]() ,
,
Thus
![]() ,
,
Hence
![]()
Then ![]() is an FLDcircr matrix.
is an FLDcircr matrix.
Theorem 5.3 If A is an FLDcircr matrix, then A is nonsingular if and only if![]() .
.
Proof. If A is a nonsingular FLDcircr matrix, from Theorem 4.2, we have![]() , so
, so ![]() and
and ![]() don’t have the same solutions, thus
don’t have the same solutions, thus![]() .
.
Otherwise, if![]() , there exist
, there exist![]() ,
, ![]() such that
such that![]() ,
, ![]() . For
. For![]() ,
, ![]() , we have
, we have![]() . So, A is nonsingular and
. So, A is nonsingular and![]() . From Theorem 3.1, we have
. From Theorem 3.1, we have ![]() is an FLDcircr matrix.
is an FLDcircr matrix.
Corollary 5.4 If A is a nonsingular FLDcircr matrix, there exits![]() .
.
Corollary 5.5 A is a singular FLDcircr matrix, there exists an FLDcircr matrix H that satisfies ![]() .
.
Proof. For A is singular, we get![]() . Suppose
. Suppose![]() ,
, ![]() ,
,
![]() , then
, then![]() . Furthermore,
. Furthermore, ![]() doesn’t have repeated root, thus,
doesn’t have repeated root, thus,
![]() , ,. So,.
, ,. So,.
Hence, there exist![]() ,
, ![]() such that
such that
![]() . (3)
. (3)
Equation (3) both sides multiplied by![]() , then
, then
![]() .
.
For![]() ,
, ![]() , we have
, we have
![]() (4)
(4)
Equation (3) both sides multiplied by![]() . Similarly, we get
. Similarly, we get
![]() . (5)
. (5)
If![]() , then H is the polynomial of D, from Theorem 3.1, we get H is an FLDcircr matrix, and from Equation (4), Equation (5) we have
, then H is the polynomial of D, from Theorem 3.1, we get H is an FLDcircr matrix, and from Equation (4), Equation (5) we have![]() .
.
Due to
![]()
![]()
Hence![]() .
.
From Lemma 2.7 and the proof of Theorem 5.3, Corollary 5.5, we can get the fast algorithm of the inverse and generalized inverse of the FLDcircr matrix. The general steps are as follows:
Step 1 get the greatest common factor ![]() of
of![]() ,
,![]() ;
;
Step 2 If![]() , the polynomial matrix
, the polynomial matrix ![]() can transformed into
can transformed into ![]() after elementary
after elementary
row transformation, then![]() ;
;
Step 3 If![]() , divide
, divide ![]() by
by![]() , get
, get![]() , then the polynomial matrix
, then the polynomial matrix ![]() can transformed into
can transformed into ![]() after elementary row transformation, hence
after elementary row transformation, hence![]() .
.
Example 5.1 If the 3 order matrix![]() , then whether A is a nonsingular matrix? If A is non-
, then whether A is a nonsingular matrix? If A is non-
singular, solving![]() .
.
From Definition 2.1 we get![]() ,
, ![]() ,
, ![]() ,
,![]() . Because of
. Because of![]() , so A is nonsingular.
, so A is nonsingular.
After a series of elementary row transformation of the following polynomial matrix, we obtain
![]()
So
![]() .
.
Therefore
![]() ,
,
That is
![]() .
.
Example 5.2 If the 3 order matrix![]() , solving
, solving![]() .
.
From Definition 2.1 we have![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Then![]() , so, A is singular and
, so, A is singular and![]() .
.
From Step 3, we get
![]()
Then
![]()
So
![]() ,
,
That is
![]() .
.
Acknowledgements
The authors are grateful to the anonymous referees for their review comments and suggestions that help to improve the original manuscript.