Construction of Three Quadrature Formulas of Eighth Order and Their Application for Approximating Series ()
1. Introduction
We consider the three-parameters families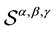 ,
, 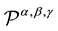 ,
, 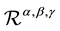 of quadrature formulas for the integral
of quadrature formulas for the integral
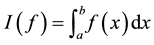 . These quadratures are linear combinations of the quadrature investigated in papers [1] - [3]
. These quadratures are linear combinations of the quadrature investigated in papers [1] - [3]
respectively. The error estimates are calculated in dependence of the parameters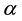 ,
, 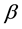 ,
, 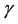 and then in some natural restrictions on them these are investigated the quadrature formulas of the 8th order. The desired con- clusions are made by means of properties of Peano kernels using substantially well-known error formulas. We construct the only one quadrature formula of the eight order which belongs to the family
and then in some natural restrictions on them these are investigated the quadrature formulas of the 8th order. The desired con- clusions are made by means of properties of Peano kernels using substantially well-known error formulas. We construct the only one quadrature formula of the eight order which belongs to the family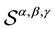 , the only one quadrature formula of the eight order too, which belongs to the family
, the only one quadrature formula of the eight order too, which belongs to the family 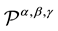 and the only one quadrature for- mula of the eight order too, which belongs to the family
and the only one quadrature for- mula of the eight order too, which belongs to the family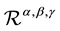 . Because of the Peano kernels for these qua- dratures have different signs, for functions whose 8th derivative is either always positive or always negative we use these quadrature formulas to get good bounds on
. Because of the Peano kernels for these qua- dratures have different signs, for functions whose 8th derivative is either always positive or always negative we use these quadrature formulas to get good bounds on . So, by suitable choice of parameters one can increase quadrature order from two or four respectively to eight.
. So, by suitable choice of parameters one can increase quadrature order from two or four respectively to eight.
2. The Three-Parameters Family of Quadrature Formulas 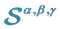
We consider family of quadrature formulas ![]() given by
given by
![]() (1)
(1)
for integral![]() . This family generalizes the family
. This family generalizes the family ![]() discussed in [1] , here it is enough to put
discussed in [1] , here it is enough to put![]() ,
, ![]() ,
,![]() .
.
For arbitrary![]() ,
, ![]() ,
, ![]() the quadrature formula
the quadrature formula ![]() is of the second order. The error
is of the second order. The error
![]() for the polynomials
for the polynomials ![]() is equal
is equal
![]()
![]()
![]()
If a triple ![]() is a root of the polynomial
is a root of the polynomial ![]() the range of quadrature
the range of quadrature
formula increases. These triples we can write in the form ![]() with
with
![]()
where![]() . Then every
. Then every ![]() is of the fourth order, and moreover
is of the fourth order, and moreover
![]()
![]()
![]()
If the pair ![]() is a root of the polynomial
is a root of the polynomial ![]() then the range of
then the range of
quadrature increases as before. We can write these pairs in the form ![]() where
where
![]()
for![]() .
.
Every quadrature ![]() is of the six order but we must restrict the interval for
is of the six order but we must restrict the interval for![]() . The quadrature
. The quadrature
nodes belongs to interval ![]() only for
only for![]() . Graphs of the functions
. Graphs of the functions
![]()
and ![]() are presented on the Figure 1.
are presented on the Figure 1.
In this case we have
![]()
![]()
![]()
The six order Peano kernel ![]() where
where![]() . This
. This
kernel is a periodic function with period h and on every interval ![]() is symmetrical respect to
is symmetrical respect to
its midpoint. So, it is enough to define it on the interval![]() :
:
![]() (2)
(2)
The kernel ![]() is negative for
is negative for ![]() and positive for
and positive for![]() . After numerical calculation we conclude that
. After numerical calculation we conclude that![]() ,
, ![]() (see Figure 2).
(see Figure 2).
The integral of the six order Peano kernel takes form
![]()
(see Figure 3).
From Peano theorem (see [5] ) the error
![]() (3)
(3)
for any function ![]() and
and![]() , where
, where![]() . Moreover, using Peano theorem we can prove the following:
. Moreover, using Peano theorem we can prove the following:
Theorem 1. If![]() ,
, ![]() , function
, function![]() , and
, and ![]() has constant sign on interval
has constant sign on interval
![]() , then
, then
![]() (4)
(4)
if ![]() is non-negative on interval
is non-negative on interval![]() , and
, and
![]() (5)
(5)
if ![]() is non-positive on interval
is non-positive on interval![]() .
.
Proof. Assume that![]() . From the formula (3), because of
. From the formula (3), because of ![]() and
and![]() , we have
, we have
![]()
Similarly
![]()
because of ![]() and
and![]() . □
. □
The function ![]() has one root
has one root
![]() . Lets put
. Lets put
![]() ,
,![]() . The quadrature
. The quadrature
formula ![]() is of the eight order and
is of the eight order and
![]()
![]()
The eight order Peano kernel ![]() where
where![]() . This kernel
. This kernel
is a periodic function with period h and on every interval ![]() symmetrical with respect to its
symmetrical with respect to its
midpoint. So us for![]() , it is enough to define it on the interval
, it is enough to define it on the interval![]() :
:
![]() (6)
(6)
(see Figure 4).
This kernel ![]() is non-negative, moreover
is non-negative, moreover
![]()
From the Peano theorem (see [5] ) we obtain for any function ![]() the expression on the error
the expression on the error
![]() (7)
(7)
where![]() .
.
3. The Three-Parameter Family of Quadrature Formulas ![]()
We consider the family of quadrature formulas of the form
![]() (8)
(8)
where
![]()
![]() ,
, ![]() ,
, ![]() is the trapezoidal rule, and
is the trapezoidal rule, and![]() ,
, ![]() ,
, ![]() are para-
are para-
meters. Particular cases ![]() and
and ![]() are investigated in the paper [2] and
are investigated in the paper [2] and![]() ,
, ![]() . We are proved that
. We are proved that ![]() and
and ![]() with
with
![]()
![]()
where ![]() and
and ![]() (see Figure 5) are of the six order. If we define the error
(see Figure 5) are of the six order. If we define the error
![]() we can compute for the polynomials
we can compute for the polynomials ![]()
![]()
![]()
![]()
where
![]()
![]()
![]()
So, for every ![]() the quadrature
the quadrature ![]() is of the six order. Let
is of the six order. Let
![]()
With ![]() the range of quadrature formula increases. The quadrature
the range of quadrature formula increases. The quadrature ![]() is of the eight order but the expression
is of the eight order but the expression ![]() takes a very complicated form.
takes a very complicated form.
The eight order Peano kernel ![]() where
where![]() . This kernel
. This kernel
is a symmetrical function respect to the point![]() , so it is enough to define it on the interval
, so it is enough to define it on the interval![]() :
:
![]() (9)
(9)
where
![]()
![]()
![]()
![]()
and![]() . On the Figure 6 we have graphs of the kernels
. On the Figure 6 we have graphs of the kernels ![]() for
for![]() . For any n the kernel
. For any n the kernel
![]() is non-positive, moreover the integral
is non-positive, moreover the integral
![]()
in the case ![]() and
and
![]()
Figure 6. Graphs of the kernels ![]() for n = 4, 5, 6.
for n = 4, 5, 6.
![]()
if![]() . From the Peano theorem (see [5] ) we obtain for any function
. From the Peano theorem (see [5] ) we obtain for any function ![]() the expression on the error
the expression on the error
![]() (10)
(10)
where ![]() and
and ![]() for all n.
for all n.
A Complex Quadrature Formula ![]()
Let![]() , the step
, the step ![]() and the nodes
and the nodes ![]()
![]() . The integral
. The integral ![]() can be written in the form
can be written in the form![]() , where
, where![]() . To each integral
. To each integral ![]() we apply the quadrature (8):
we apply the quadrature (8):
![]() (11)
(11)
where now![]() ,
,
![]() ,
, ![]() ,
,![]() . Next we define
. Next we define
![]() (12)
(12)
Obviously![]() . For every
. For every![]() , the quadrature formula
, the quadrature formula ![]() is of the six order and
is of the six order and ![]() is of the eight order. The Peano kernel for the quadrature formula
is of the eight order. The Peano kernel for the quadrature formula ![]() is a periodic function with period k and on every interval
is a periodic function with period k and on every interval ![]() is symmetrical with respect to its midpoint. The quadrature formula (12) has
is symmetrical with respect to its midpoint. The quadrature formula (12) has ![]() nodes.
nodes.
Because of Peano kernels for quadrature formulas![]() ,
, ![]()
![]() have different signs, we have the following theorem.
have different signs, we have the following theorem.
Theorem 2. If function![]() , and the derivative
, and the derivative ![]() has constant sign on interval
has constant sign on interval![]() , then
, then
![]() (13)
(13)
if ![]() is non-negative on the interval
is non-negative on the interval![]() , and
, and
![]() (14)
(14)
if ![]() is non-positive on the interval
is non-positive on the interval![]() .
.
Proof. Assume that![]() . From the formula (7) we have
. From the formula (7) we have
![]()
because of ![]() and
and![]() . Similarly from the formula (10):
. Similarly from the formula (10):
![]()
because of ![]() and
and![]() . □
. □
4. The Three-Parameter Family of Quadrature Formulas ![]()
We consider the family of quadrature formulas of the form
![]() (15)
(15)
where
![]()
![]() ,
, ![]() ,
, ![]() is the midpoint rule, and
is the midpoint rule, and![]() ,
, ![]() ,
, ![]() are parameters. Parti-
are parameters. Parti-
cular cases ![]() and
and ![]() are investigated in the paper [3] and
are investigated in the paper [3] and![]() ,
,
![]() . We are proved that
. We are proved that ![]() and
and ![]() with
with
![]()
![]()
where
![]()
are of the six order. If we define the error ![]() we can compute for the polynomials
we can compute for the polynomials ![]()
![]()
![]()
where
![]()
![]()
![]()
So, for every ![]() the quadrature
the quadrature ![]() is of the six order. Let
is of the six order. Let
![]()
(see Figure 7).
With ![]() the range of quadrature formula increases. The quadrature
the range of quadrature formula increases. The quadrature ![]() is of the eight order but the expression
is of the eight order but the expression ![]() takes a very complicated form.
takes a very complicated form.
The eight order Peano kernel ![]() where
where![]() . This kernel is a symmetrical function respect to the point
. This kernel is a symmetrical function respect to the point![]() , so it is enough to define it on the interval
, so it is enough to define it on the interval![]() :
:
![]() (16)
(16)
where
![]()
![]()
![]()
![]()
and![]() . On the Figure 8 we have graphs of the kernels
. On the Figure 8 we have graphs of the kernels ![]() for
for![]() . For any n the kernel
. For any n the kernel
![]() is non-negative, moreover the integral
is non-negative, moreover the integral
![]() (17)
(17)
where
![]()
Figure 8. Graphs of the kernels ![]() for n = 4, 5, 6.
for n = 4, 5, 6.
![]()
![]()
![]()
![]()
![]()
![]()
and
![]()
![]()
![]()
![]()
![]()
From the Peano theorem (see [5] ) we obtain for any function ![]() the expression on the error
the expression on the error
![]() (18)
(18)
where ![]() and
and ![]() for all n.
for all n.
Theorem 3. If function![]() , and the derivative
, and the derivative ![]() has constant sign on interval
has constant sign on interval![]() , then
, then
![]() (19)
(19)
if ![]() is non-negative on the interval
is non-negative on the interval![]() , and
, and
![]() (20)
(20)
if ![]() is non-positive on the interval
is non-positive on the interval![]() .
.
Proof. Assume that![]() . From the formulas (10) and (18):
. From the formulas (10) and (18):
![]()
because of ![]() and
and ![]() and
and
![]()
because of ![]() and
and![]() . □
. □
5. Series Estimation
The sum of a series
![]() (21)
(21)
can be approximated by a finite sum![]() . The error of this estimation can be represented as the sum of the series
. The error of this estimation can be represented as the sum of the series ![]()
Therefore, if we have a method of estimating the sum of an infinite series, then this method will enable us to estimate the error of the N-term approximation. One way to estimate the sum of the series is to take into conside- ration the fact that a series can be viewed as an integral over an infinite domain
![]() (22)
(22)
for some function ![]() for which
for which ![]() for all n. Therefore, if for a given series, we know
for all n. Therefore, if for a given series, we know
an explicitly integrable function ![]() with this property, then we can take the value
with this property, then we can take the value ![]() of the integral as an estimate for s.
of the integral as an estimate for s.
Theorem 4. We assume that the function f is such that
1) f is either positive and decreasing, or negative and increasing.
2) ![]() is convergent.
is convergent.
3)![]() .
.
4) ![]() is either positive or negative on
is either positive or negative on![]() .
.
5)![]() .
.
6)![]() .
.
Under this assumptions, if ![]() then
then
![]() (23)
(23)
where
![]()
![]()
If![]() , then we get a similar inequality, but with the right-hand side instead of the left-hand side, and vice versa.
, then we get a similar inequality, but with the right-hand side instead of the left-hand side, and vice versa.
Proof. First, from the inequalities (19) we have:
![]()
We can rewrite this inequality in an equivalent form:
![]() (24)
(24)
In this inequality we put:![]() ,
, ![]() ,
, ![]() ,
, ![]() so
so
![]()
![]()
Because of
![]()
than passing with n to ![]() in the inequality (24) we obtain
in the inequality (24) we obtain
![]()
We complete the first part of the proof by adding the term ![]() to the both sides of this inequality.
to the both sides of this inequality.
Let![]() . From the inequalities (19) we have:
. From the inequalities (19) we have:
![]()
We rewrite this inequality in an equivalent form:
![]()
and put:![]() ,
, ![]() ,
, ![]() ,
,![]() . Passing with
. Passing with ![]() to
to ![]() we obtain
we obtain
![]() (25)
(25)
because of
![]()
We complete the proof by adding the term ![]() to the both sides of the inequality (25). □
to the both sides of the inequality (25). □
Acknowledgements
We thank the editor and the referee for their comments.