1. Introduction
Besides the study of the isomorphism classes and in order to complete the study of the crystal families of space E5, five families are studied in this paper:
1) The crystal families N˚XXIII (monoclinic di iso squares)-al, N˚XXIV decadic-al and N˚XXV (monoclinic di iso hexagons)-al. The suffix “al” means that the family cell in space E5 is a right hyper prism based on a cell of space E4. The WPV holohedry symbols are ([8] 2 2)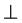 m, group of order 32 for the family N˚XXIII, ([10] 2 2)
m, group of order 32 for the family N˚XXIII, ([10] 2 2)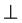 m, group of order 40 for the family N˚XXIV and ([12] 2 2)
m, group of order 40 for the family N˚XXIV and ([12] 2 2) m, and group of order 48 for the family N˚XXV. These families have 7, 12, and 7 crystallographic (cr) point groups respectively. We remark that the WPV symbol of the holohedry of these families contains double rotations of order 8, 10 and 12 (Paragraphs 2, 3 and 4).
m, and group of order 48 for the family N˚XXV. These families have 7, 12, and 7 crystallographic (cr) point groups respectively. We remark that the WPV symbol of the holohedry of these families contains double rotations of order 8, 10 and 12 (Paragraphs 2, 3 and 4).
2) The crystal families N˚XXX (rhombotopic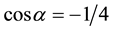 )-al and N˚XXXII rhombotopic
)-al and N˚XXXII rhombotopic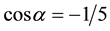 . The meaning of these names will be given in Paragraphs 5 and 6. The family N˚XXX splits in two sub-families:
. The meaning of these names will be given in Paragraphs 5 and 6. The family N˚XXX splits in two sub-families:
the centred family N˚XXXa with group 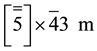 of order 240 for holohedry and 8 cr point groups; the
of order 240 for holohedry and 8 cr point groups; the
primitive family N˚XXX with group 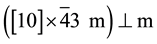 of order 480 for holohedry and 15 cr point groups.
of order 480 for holohedry and 15 cr point groups.
The WPV holohedry symbol of family N˚XXXII is  of order 1440 and this family has 10
of order 1440 and this family has 10
cr point groups. Some cr point groups of the family N˚XXX are obtained from those of the rhombotopic  family of space E4 while all the 10 cr point groups of the family N˚XXXII belong to space E5. Moreover, this family is one of the irreducible families of space E5 [1] .
family of space E4 while all the 10 cr point groups of the family N˚XXXII belong to space E5. Moreover, this family is one of the irreducible families of space E5 [1] .
The mark “×” means direct product.
To end the study of the crystal families of space E5, the crystal families (hypercube 4 dim.)-al (N˚XXVIII), (di iso hexagons)-al (N˚XXIX) and hypercube 5 dim. N˚XXXI will be described in the next paper.
The results about the cr point groups are obtained from our Scientific Software SS E5 (explanations are given paper N˚1).
2. (Monoclinic di iso Squares)-al Crystal Family. Point Groups. Isomorphism Classes
2.1. Recall
Let be denoted 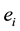
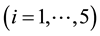 , the 5 vectors of a basis of space E5. The metric tensor of the quadratic form defining a cell is a symmetric tensor with the scalar products
, the 5 vectors of a basis of space E5. The metric tensor of the quadratic form defining a cell is a symmetric tensor with the scalar products .
.  as elements
as elements .
.
2.2. Cell of the (Monoclinic di iso Squares)-al Crystal Family (N˚ XXIII)
The cell of the “(monoclinic di iso squares)-al” family is a right hyper prism, generalization of the right prism of space E3. The word “al” is the abbreviation of the adjective orthogonal”.
The metric tensor of the quadratic form defining the cell of this family is as follows (matrix N˚1):
Matrix N˚1 associated with the cell of the (monoclinic di iso squares)-al family
![]()
Caption ![]()
As the name suggests, this cell is a right hyper prism which basis is built from two equal squares in space E4. These two squares are built in the planes defined by the axes ![]() for the first one and by the axes
for the first one and by the axes ![]() for the second one; these two planes are not orthogonal but the angles between them depend on one angular parameter b. It is the reason why the word “monoclinic” appears in the family name. One of the two length parameters is the length
for the second one; these two planes are not orthogonal but the angles between them depend on one angular parameter b. It is the reason why the word “monoclinic” appears in the family name. One of the two length parameters is the length ![]() of the two square sides, the other one is the length
of the two square sides, the other one is the length ![]() of the edge of the hyper prism (see the caption of the matrix N˚1).
of the edge of the hyper prism (see the caption of the matrix N˚1).
The angles between the axes ![]() and
and ![]() on one hand, between the axes
on one hand, between the axes ![]() and
and ![]() on the other hand have equal values while the axis
on the other hand have equal values while the axis ![]() is orthogonal to the space defined by the axes
is orthogonal to the space defined by the axes![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
2.3. Crystallographic Point Groups of the (Monoclinic di iso Squares)-al Family
The WPV symbols of all cr (cr for crystallographic) point groups of the family (monoclinic di iso squares)-al
contain groups ![]() or
or ![]() either alone or as product with one or two binary groups such as m, 2,
either alone or as product with one or two binary groups such as m, 2,![]() . It is a
. It is a
characteristic property of the cr point groups of this family. We recall that [8] is the WPV symbol of the cyclic group generated by the double rotation through angles ![]() and
and ![]() denoted 8183, these two rotations 81 and 83 take place into the planes
denoted 8183, these two rotations 81 and 83 take place into the planes ![]() and
and![]() . The elements of the cyclic group [8], isomorphic to group C8, are 8183, 4143, 8381,
. The elements of the cyclic group [8], isomorphic to group C8, are 8183, 4143, 8381, ![]() , 8587, 4341, 8785, 1.
, 8587, 4341, 8785, 1.
In the same way, ![]() is the WPV symbol of a cyclic group of order 8 generated by the symmetry operation
is the WPV symbol of a cyclic group of order 8 generated by the symmetry operation![]() ,
, ![]() being the total homothetie of space E5. The group
being the total homothetie of space E5. The group ![]() has for elements 8183mu, 4143, 8381mu,
has for elements 8183mu, 4143, 8381mu, ![]() ,
,
8587mu, 4341, 8785mu, 1, where u is the unit vector of the axis e5 orthogonal to space E4.
Group ![]() cannot be confused with the following two groups of order 16,
cannot be confused with the following two groups of order 16, ![]() and
and![]() , the last
, the last
one acts into a space of dimension 9 = 4 + 5 and belongs to the crystal family “(monoclinic di iso squares) decaclinic”.
Table 1 lists the seven cr point groups of family XXIII which belong to four isomorphism classes, C8, D8, C8 × C2, D8 × C2, D8 is the dihedral group of order 16 (see Annex, paper N˚I).
Remark
WPV symbols![]() ,
, ![]() , and
, and ![]() of the groups of the isomorphism class D8 are very similar
of the groups of the isomorphism class D8 are very similar
to Hermann-Mauguin symbols 4 mm, 422, ![]() (groups of the isomorphism class D4).
(groups of the isomorphism class D4).
3. (Monoclinic di iso Hexagons)-al Crystal Family. Point Groups. Isomorphism Classes
3.1. Cell of the (Monoclinic di iso Hexagons)-al Crystal Family (N˚XXV)
Family N˚XXV, (monoclinic di iso hexagons)-al, presents great similarities with family N˚XXIII (monoclinic di iso squares)-al. The metric tensor of the quadratic form defining the cell of this family is as follows (matrix N˚2):
Matrix N˚2 associated with the cell of the (monoclinic di iso hexagons)-al family in space E5
![]()
Caption: ![]()
The cell of this family is a righthyper prism which basis in space E4 is built from two equal hexagons into the planes defined by the axes ![]() for the first one and by the axes
for the first one and by the axes ![]() for the second one; these planes are not orthogonal and the angles between these two planes depend on one angular parameter b. It is the reason
for the second one; these planes are not orthogonal and the angles between these two planes depend on one angular parameter b. It is the reason
![]()
Table 1. Crystallographic point groups of (monoclinic di iso squares)-al family of space E5.
Table caption: First column: Symbols of the isomorphism classes. Second column: Order classes. Third column: WPV symbol of the point groups of the (monoclinic di iso squares)-al family in space E4. Fourth column: WPV symbol of the point groups of the (monoclinic di iso squares)-al family in space E5. Fifth column: Lists of the elements of the isomorphism classes denoted arrangement. SS E5 gives this information.
why the word “monoclinic” appears in the family name. One of the two length parameters is the length ![]() of the two hexagon sides, the other one is the length
of the two hexagon sides, the other one is the length ![]() of the edge of the hyper prism, b is the angular parameter (see caption of matrix N˚2).
of the edge of the hyper prism, b is the angular parameter (see caption of matrix N˚2).
3.2. Crystallographic Point Groups of the (Monoclinic di iso Hexagons)-al Crystal Family
All WPV point group symbols of this family contain the group [12] or ![]() either alone or as product with
either alone or as product with
one or two binary groups such as m, 2,![]() . It is a characteristic property of the cr point groups of this family.
. It is a characteristic property of the cr point groups of this family.
We recall that [12] is the WPV symbol of the cyclic group of order 12, isomorphic to group C12. It is generated by the double rotation 121125 through angles 2π/12 and 5 × 2π/12, each of these rotations 121 and 125 takes place into the planes ![]() and
and![]() . The group [12] elements are the following ones 121125, 6165, 4141,
. The group [12] elements are the following ones 121125, 6165, 4141,
3132, 125121, ![]() , 1271211, 3231, 4343, 6561, 1211127, 1. In the same way, the group denoted
, 1271211, 3231, 4343, 6561, 1211127, 1. In the same way, the group denoted ![]() is the WPV
is the WPV
symbol of the cyclic group of order 12 generated by the symmetry operation ![]() or 1271211mu. The ele-
or 1271211mu. The ele-
ments of the group ![]() are 1271211mu, 6165, 4343mu, 3132, 1211127mu,
are 1271211mu, 6165, 4343mu, 3132, 1211127mu, ![]() , 121125mu, 3231, 4141mu, 6561,
, 121125mu, 3231, 4141mu, 6561,
125121mu, 1.
Group ![]() cannot be confused with the following two groups of order 24,
cannot be confused with the following two groups of order 24, ![]() and
and![]() , the last group acting into a space of dimension 9 = 4 + 5.
, the last group acting into a space of dimension 9 = 4 + 5.
Table 2 lists the seven cr point groups of family N˚XXV, these groups belong to four isomorphism classes C12, D12, C12 × C2, D12 × C2 (D12 is the dihedral group of order 24).
Remark
WPV symbols![]() ,
, ![]() and
and ![]() of the groups of the isomorphism class D12 are very
of the groups of the isomorphism class D12 are very
similar to Hermann-Mauguin symbols 4 mm, 422, ![]() (groups of the isomorphism class D4).
(groups of the isomorphism class D4).
4. Decadic-al Crystal Family. Point Groups. Isomorphism Classes 6
4.1. Cell of the Decadic-al Crystal Family (N˚ XXIV)
The word “decadic” means that double rotations of order 10 belong to several cr point groups of this family.
The cell of the decadic-al family is a right hyper prism, the basis of which is a particular parallelotope of space E4. The faces of this cell are equal lozenges in planes ![]() and
and![]() , so are the faces in planes
, so are the faces in planes ![]() and
and ![]() but these lozenges are different from the previous ones. The metric tensor of the quadratic form of the decadic-al family is as follows:
but these lozenges are different from the previous ones. The metric tensor of the quadratic form of the decadic-al family is as follows:
![]()
Table 2. Crystallographic point groups of (monoclinic di iso hexagons)-al family.
Table caption: First column: Symbols of the isomorphism classes. Second column: Order of these classes. Third column: WPV symbol of the point groups of the (monoclinic di iso hexagons)-al family in space E4. Fourth column: WPV symbol of the point groups of the (monoclinic di iso hexagons)-al family in space E5. Fifth column: Lists of the elements of the isomorphism classes. SS E5 gives this information.
Matrix N˚3 associated with the cell of the (monoclinic di iso hexagons)-al family
![]()
Caption: ![]()
This metric tensor depends on three parameters of length a, b and c; the parameter ![]() is the length of the side of the first lozenge,
is the length of the side of the first lozenge, ![]() the one of the second lozenge and
the one of the second lozenge and ![]() the hyperprism side. The angles between the axes depend on the two parameters a and b.
the hyperprism side. The angles between the axes depend on the two parameters a and b.
Family N˚XXIV splits in two sub-families, the centred sub-family N˚XXIVa and the primitive sub-family N˚XXIV.
4.2. Crystallographic Point Groups of the Two Decadic-al Crystal Sub-Families
All the WPV point group symbols of these two families contain groups ![]() or
or ![]() (family N˚XXIVa) and
(family N˚XXIVa) and
group [10] (family N˚XXIV) either alone or as product with a binary group such as 2, ![]() , m, ・・・ It is a charac-
, m, ・・・ It is a charac-
teristic property of the cr point groups of these families. Symbols![]() ,
, ![]() ,
, ![]() have the same meaning as
have the same meaning as
[8] and ![]() or
or ![]() and
and ![]() (see Paragraphs 2-3 and 3-2).
(see Paragraphs 2-3 and 3-2).
The five cr point groups of the sub-family N˚XXIVa belong to four isomorphism classes C5, D5, C10 = C5 × C2, D10 = D5 × C2 and the seven cr point groups of the sub-family N˚XXIV belong to four isomorphism classes C10, D10, C10 × C2, D10 × C2. Groups D5 and D10 are dihedral groups of orders 10 and 20. Table 3 gives the list of the point groups of the decadic-al sub-families. Only groups of centred sub-family XXIVa are pointed out.
Remarks
・ One group of class C10 belongs to the centred sub-family and two to the primitive sub-family.
・ ![]() . This group is a cyclic group of order 10, generated by the symmetry 101103mu operation. Its
. This group is a cyclic group of order 10, generated by the symmetry 101103mu operation. Its
elements are 101103mu, 5153, 103109mu, 5251, ![]() , 535 4, 107101mu, 5452, 109107mu, 1. We explain how the planes of the double rotation 101103 can be defined. Indeed,thanks to the symmetry operation list, it is easy to find the generators of the different cr point groups. With respect to the general basis
, 535 4, 107101mu, 5452, 109107mu, 1. We explain how the planes of the double rotation 101103 can be defined. Indeed,thanks to the symmetry operation list, it is easy to find the generators of the different cr point groups. With respect to the general basis![]() , e2, e3, e4, e5 or x, y, z, t, u, the double rotation [10] is generated by the symmetry operation described by the following matrix A:
, e2, e3, e4, e5 or x, y, z, t, u, the double rotation [10] is generated by the symmetry operation described by the following matrix A:
![]()
Table 3. Crystallographic point groups of the two decadic-al sub-families.
Table caption: First column: Symbol of the isomorphism classes. Second column: Order of these classes. Third column: WPV symbols of the point groups of the decadic-al family in space E4. Fourth column: WPV symbols of the point groups of the decadic-al family in space E5. Fifth column: Lists of the symmetry elements with their number of every isomorphism class.
Matrix N˚4 associated with the double rotation 101103
![]()
It is possible to calculate the roots of the characteristic polynomial of the matrix ![]() and the eigen subspaces associated to the different eigen values. As the double rotation [10] takes place in a four-dimensional space, the eigenvalue 1 appears. The other eigen values of the matrix
and the eigen subspaces associated to the different eigen values. As the double rotation [10] takes place in a four-dimensional space, the eigenvalue 1 appears. The other eigen values of the matrix ![]() are
are ![]() and
and![]() . This double rotation 101103 takes place in the two planes defined by the axes:
. This double rotation 101103 takes place in the two planes defined by the axes:
![]() and
and ![]() for the rotation 101
for the rotation 101
![]() ,
, ![]() for the rotation 103.
for the rotation 103.
The coefficients which define the planes are
![]()
![]()
For all the symmetry operations of the group, we repeat the same process. For instance, the double rotation [5] is generated by the element 5153 which is described by the matrix![]() :
:
Matrix N˚5 associated with the double rotation 5153
![]()
The eigenvalues are numbers ![]() and
and ![]() and 1. The same process leads to the same eigen subspaces for double rotation [5] as for double rotation [10].
and 1. The same process leads to the same eigen subspaces for double rotation [5] as for double rotation [10].
5. (Rhombotopic![]() )-al Crystal Family. Point Groups. Isomorphism Classes
)-al Crystal Family. Point Groups. Isomorphism Classes
The crystal family N˚XXX splits into two sub-families, one primitive sub-family N˚XXX, one centred sub-family N˚XXXa. This family is a particular case of the (rhombotopic![]() )-al family. The cell of this family is a right hyper prism which basis is a regular rhombotope. We remind some properties of these types of cells.
)-al family. The cell of this family is a right hyper prism which basis is a regular rhombotope. We remind some properties of these types of cells.
5.1. Generalities about the (Rhombotopic![]() )-al Family
)-al Family
The cell of the (rhombotopic![]() )-al family is a right hyperprism of the
)-al family is a right hyperprism of the ![]() -dimensional space. The base of this cell is a regular rhombotope of the n-dimensional space. The metric tensor associated to the basis in space En + 1 is the matrix N˚6. The n vectors of the lattice basis of the space En have the same norm
-dimensional space. The base of this cell is a regular rhombotope of the n-dimensional space. The metric tensor associated to the basis in space En + 1 is the matrix N˚6. The n vectors of the lattice basis of the space En have the same norm ![]() and the cosine of the angle between two of them is
and the cosine of the angle between two of them is![]() . The norm of the
. The norm of the ![]() vector is
vector is ![]() and this vector is orthogonal to space En.
and this vector is orthogonal to space En.
Matrix N˚6 associated with the cell of the (rhombotopic![]() )-al crystal family
)-al crystal family
![]()
Caption: ![]()
5.1.1. Description of Some Simplexes
A simplex is the generalization of a triangle. Any set of ![]() points which do not lie in one
points which do not lie in one ![]() -di- mensional space are the vertices of an n-dimensional simplex. A regular simplex has all edges equal, all faces equal and so on. For instance, regular simplexes are the equilateral triangle (space E2), the regular tetrahedron (space E3), the regular pentatope (space E4) in [2] [3] .
-di- mensional space are the vertices of an n-dimensional simplex. A regular simplex has all edges equal, all faces equal and so on. For instance, regular simplexes are the equilateral triangle (space E2), the regular tetrahedron (space E3), the regular pentatope (space E4) in [2] [3] .
A regular simplex is not a crystal cell in (E3). To obtain a crystal cell, we must add a second regular simplex symmetrical to the previous one at the centre of the initial cell and so the lattice of the crystal (rhombotopic![]() ) family is obtained.
) family is obtained.
Some additional properties are given in the Annex.
5.1.2. Point Groups of the Simplexes and of the (Rhombotopic![]() ) Family
) Family
Now, it is easy to find the WPV point groups of some regular simplexes and the holohedries of the associated crystallographic family together with its order. Table 4 gives point groups of some simplexes and of some rhombotopic crystal families.
[7] is the abridged WPV symbol of a cyclic group of order 7 generated by the triple rotation of space E6,![]() .
.
5.2. Primitive (Rhombotopic![]() )-al Sub-Family
)-al Sub-Family
The cell of the primitive (rhombotopic![]() )-al sub-family is a right hyper prism which basis is the regular rhombotope of space E4. Hence, the previous results are applicable. This family can be considered as a particular case of the decadic-al family if the parameter b is equal to
)-al sub-family is a right hyper prism which basis is the regular rhombotope of space E4. Hence, the previous results are applicable. This family can be considered as a particular case of the decadic-al family if the parameter b is equal to![]() .
.
The metric tensor of the quadratic form of the primitive family N˚XXX is as follows (matrix N˚7):
Matrix N˚7 associated with the cell of the (rhombotopic![]() )-al family
)-al family
![]()
Caption: ![]()
This metric tensor depends on two parameters of length a and c.
![]()
Table 4. Crystallographic point groups of some regular simplexes and of the (rhombotopic![]() ) family holohedries.
) family holohedries.
Table caption: First column: WPV point group symbols of simplexes. Second column: Order of these point groups. Third column: Space of these simplexes. Fourth column: WPV symbol holohedries of the (rhombotopic![]() ) families. Fifth column: Order of these point groups.
) families. Fifth column: Order of these point groups.
5.3. Isomorphism Classes of the Two Sub-Families (Rhombotopic![]() )-al of Space E5
)-al of Space E5
The isomorphism classes have point groups belonging to the two sub-families N˚XXXa and N˚XXX so that it is useful to gather them, only groups of sub-family N˚XXXa are pointed out. To sum up, the eight cr point groupsof sub-family N˚XXXa and the five teen cr point groups of sub-family N˚XXX belong to nine isomorphism classes. Table 5 gives all this results.
Remarks
・ In the isomorphism class S5 × C2, only one group, [10] × (42 3 2), is a positive point group, two groups are of the type g4![]() m with group g4 acting in space E4.
m with group g4 acting in space E4.
・ The list of symmetry operations of all cr point groups of space E5 established by Veysseyre [4] gives ten mirrors to the group![]() . The symmetry group of the regular tetrahedron
. The symmetry group of the regular tetrahedron ![]() has six mirrors. The(rhombotopic
has six mirrors. The(rhombotopic![]() )-al cell is bounded by five regular tetrahedrons, therefore, we can expect to find 6 × 5 = 30 mirrors, but each mirror of this cell belongs to three adjacent tetrahedrons, then, it remains 30/3 = 10 different mirrors. In the same way, the list of the symmetry operations gives ten symmetry operations
)-al cell is bounded by five regular tetrahedrons, therefore, we can expect to find 6 × 5 = 30 mirrors, but each mirror of this cell belongs to three adjacent tetrahedrons, then, it remains 30/3 = 10 different mirrors. In the same way, the list of the symmetry operations gives ten symmetry operations ![]() to the group
to the group![]() . To each mirror m, we can associate a total homothetie
. To each mirror m, we can associate a total homothetie ![]() of space E4 orthogonal to the mirror. It is the reason why we find the same number of mirrors and of total homotheties.
of space E4 orthogonal to the mirror. It is the reason why we find the same number of mirrors and of total homotheties.
・ Groups (42 3 2) and ![]() are two iso cubic groups isomorphic to cr cubic point group
are two iso cubic groups isomorphic to cr cubic point group![]() . Iso cubic point groups have been defined and studied in [5] .
. Iso cubic point groups have been defined and studied in [5] .
![]()
Table 5. Crystallographic point groups of the two (rhombotopic![]() )-al sub-families.
)-al sub-families.
Table caption: First column: Symbols of the isomorphism classes and these orders. Second column: Lists of the symmetry elements with their number of every isomorphism class. Third column WPV symbols of the point groups of the (rhombotopic![]() )-al family in space E4. Fourth column: WPV symbols of the point groups of the (rhombotopic
)-al family in space E4. Fourth column: WPV symbols of the point groups of the (rhombotopic![]() )-al family in space E5.
)-al family in space E5.
6. Rhombotopic ![]() Crystal Family. Point Groups. Isomorphism Classes
Crystal Family. Point Groups. Isomorphism Classes
This family (N˚XXXII) is a particular case of the families studied Paragraph 5-1. The metric tensor of the quadratic form of family XXXII is as follows (Matrix N˚8):
Matrix N˚8 associated with the cell of the rhombotopic ![]() family
family
![]()
Caption: ![]()
The ten point groups of the irreductible family N˚XXXII are listed Table 6, they act in five-dimensional space and they belong to eight isomorphism classes.
7. Conclusions
Thanks to the geometric approach, thanks to the study of the isomorphism classes of cr point groups in spaces E2, E3, E4 and E5 and thanks to the Hermann-Mauguin or WPV symbols, we prove that substitutions groups, cr point groups, molecular or polytope symmetry groups are strongly correlated. Cayley’s theorem anticipates this property. Let us verify these properties through Table 7 and Table 8.
Table 7 lists some cr point groups isomorphic to mathematic groups Cn and Dn, from ![]() to
to![]() . The numbers of the families 60 and 61 are given in [6] .
. The numbers of the families 60 and 61 are given in [6] .
・ [7] is the symbol of a cyclic group of order 7, in space E6. It is generated by the triple rotation 717273 through angles 2π/7, 2 × 2π/7 and 3 × 2π/7; each of these rotations 71, 72 and 73 takes place into the planes![]() ,
, ![]() and
and![]() . The elements of group [7] are the following ones: 717273, 727476, 737672, 747175, 757371, 767574, and 1. All these elements, except for 1, are of order 7.
. The elements of group [7] are the following ones: 717273, 727476, 737672, 747175, 757371, 767574, and 1. All these elements, except for 1, are of order 7.
・ [9] is the symbol of a cyclic group of order 9, in space E6. It is generated by the triple rotation 919294 through angles 2π/9, 2 × 2π/9 and 4 × 2π/9; each of these rotations 91, 92 and 94 takes place into the planes![]() ,
, ![]() and
and ![]() of space E6. The elements of group [9] are the following ones: 919294, 929498, 313231, 949897, 959192, 323132, 979591, 989795, and 1; two elements of this group are of order 3, and the other ones are of order 9, except for 1.
of space E6. The elements of group [9] are the following ones: 919294, 929498, 313231, 949897, 959192, 323132, 979591, 989795, and 1; two elements of this group are of order 3, and the other ones are of order 9, except for 1.
![]()
Table 6. Crystallographic point groups of the rhombotopic ![]() crystal family.
crystal family.
Table caption: First column: Symbols of the isomorphism classes. Second column: Orders of these classes. Third column: WPV symbols of the cr point groups of the rhombotopic ![]() family in space E5. Fourth column: Lists of the symmetry elements with their number of every isomorphism class.
family in space E5. Fourth column: Lists of the symmetry elements with their number of every isomorphism class.
![]()
Table 7. Examples of crystallographic point groups isomorphic to mathematic groups Cn and Dn![]() .
.
Table caption: First column and fourth column: Symbols of the isomorphism classes. Second column and fifth column: WPV symbols of the point groups. Third column: Generators of the point groups. Sixth column: Family names.
![]()
Table 8. Crystallographic point groups isomorphicto mathematic groups D4, D8, D5 and D10 of spaces E4 and E5.
Table caption: First column: Symbols of the isomorphism classes. Second column: Lists of the symmetry elements with their number of every isomorphism class. Third column: WPV symbols of the dihedralpoint groups in space E4. Fourth column: WPV symbols of the dihedral cr point groups in space E5. Fifth column: Names of the crystal families.
・ [11] is the symbol of a cyclic group of order 11, in space E8. It is generated by a «quadruple» rotation 111112113114 through angles 2π/11, 2 × 2π/11, 3 × 2π/11 and 4 × 2π/11; each of these rotations 111, 112, 113 and 114 takes place into the planes![]() ,
, ![]() ,
, ![]() and
and ![]() of space E8. The elements of group [11] are the following ones: 111112113114, 112114116118, 1131161191112, 114118111115, 1151110114119, 116111117112, 1171131110116, 1181151121110, 1191171110115, 1110119118117, and 1; all the elements of this group are of order 11, except for 1.
of space E8. The elements of group [11] are the following ones: 111112113114, 112114116118, 1131161191112, 114118111115, 1151110114119, 116111117112, 1171131110116, 1181151121110, 1191171110115, 1110119118117, and 1; all the elements of this group are of order 11, except for 1.
In the same way, [13] is the symbol of a cyclic group of order 13, in space E8. It is generated by a «quadruple» rotation 131132133134 through angles 2π/13, 2 × 2π/13, 3 × 2π/13 and 4 × 2π/13. The elements of this group are obtained as previously.
Table 8 gives the list of the cr point groups of the isomorphism classes D8, D12, D5 and D10 of the spaces E4 and E5.
If you like mathematic crystallography, it is easy to prove and to generalize these results to space En whatever the dimension of space is.
Annex
Some Additional Results about the Symmetry of the Polyhedrons, Molecules, Holohedries of the Crystal Families in Spaces E2, E3, E4, E5, ・・・
The definition of the simplexes with their properties has been given Paragraph 5-1.
Crystal family segment in space E1: the holohedry m is a realization of mathematic group S2 or D2 with the list of element 1(2), in the set of the two cr point groups in E1 (1, m). This symbol means that the segment is bounded by two points. The mirror, a point, is the middle of the segment.
Crystal family hexagon in space E2: the hemihedry 3 m is a realization of the mathematic group D3 of order 6 with the list of elements 2(3) 3(2), in the set of the ten cr point groups of space E2. This symbol means that the equilateral triangle is bounded by three equal segments. As an example, we can cite the chemisorbed (in a mono molecular layer) molecule BF3.
The holohedry 3 m × 2 = 6 mm of order 12 is a realization of the mathematic group D3 × C2, with the list of elements 2(6) 2(3) 7(2). This symbol means that the regular hexagon in space E2 is bounded by six equal segments. As example, we can cite the chemisorbed benzene molecule C6H6.
Crystal family cubic in space E3: the hemihedry ![]() is a realization of the mathematic group S4 of order 24, with the list of elements 6(4) 8(3) 9(2), in the set of the thirty-two cr point groups of space E3. This symbol means that the regular tetrahedron in space E3 is bounded by four equilateral triangles. Group
is a realization of the mathematic group S4 of order 24, with the list of elements 6(4) 8(3) 9(2), in the set of the thirty-two cr point groups of space E3. This symbol means that the regular tetrahedron in space E3 is bounded by four equilateral triangles. Group ![]() is the symbol of the cr point group of the molecule SiH4 (or Td Schöenflies symbol) and the one of the crystal ZnO (blende) which has F
is the symbol of the cr point group of the molecule SiH4 (or Td Schöenflies symbol) and the one of the crystal ZnO (blende) which has F ![]() as space group (International Tables of Crystallography) or
as space group (International Tables of Crystallography) or ![]() Schöenflies symbol).
Schöenflies symbol).
The holohedry ![]() is a realization of the mathematic group S4 × C2 of order 48 with the list of elements 8(6) 12(4) 8(3) 19(2), in same set of the point groups of space E3. This symbol means that the cube in space E3 is bounded by six equal squares. This symbol is the symmetry group of the regular octahedron, Oh or of the molecule Co(OH)6.
is a realization of the mathematic group S4 × C2 of order 48 with the list of elements 8(6) 12(4) 8(3) 19(2), in same set of the point groups of space E3. This symbol means that the cube in space E3 is bounded by six equal squares. This symbol is the symmetry group of the regular octahedron, Oh or of the molecule Co(OH)6.
Crystal family rhombotopic ![]() in space E4: the hemihedry
in space E4: the hemihedry ![]() is a realization of the mathematic group S5 of order 120 with the list of elements 24(5) 20(6) 30(4) 20(3) 25(2) in the set of the 227 cr
is a realization of the mathematic group S5 of order 120 with the list of elements 24(5) 20(6) 30(4) 20(3) 25(2) in the set of the 227 cr
point groups of space E4. The holohedry WPV symbol ![]() is a realization of the
is a realization of the
mathematic group S5 × C2 of order 240, with the list of elements 24(10) 24(5) 60(6) 60(4) 20(3) 51(2) in the set of the 227 cr point groups of space E4. This symbol means that the cell of this family, in space E4, is bounded by ten regular tetrahedrons.
Crystal family rhombotopic ![]() in space E5: the hemihedry
in space E5: the hemihedry ![]() is a realization of the mathematic group S6 of order 720 with the list of elements 144(5) 240(6) 180(4) 80(3) 75(2) in the set of the
is a realization of the mathematic group S6 of order 720 with the list of elements 144(5) 240(6) 180(4) 80(3) 75(2) in the set of the
955 cr point groups of space E5. The holohedry ![]() is a realization of the
is a realization of the
mathematic group S6 × C2 of order 1440, with the list of elements 144(10) 144(5) 560(6) 360(4) 80(3) 151(2) among the set of the point groups of space E5. The holohedry symbol means that the cell of this family is bounded by twelve regular rhombotopes of space E4.
NOTES
*Corresponding author.