Determination of Shearing Properties for Tubular Pinewood under Torsion ()
1. Introduction
Wood is modeled as a fiber composite material of transversely isotropic type. The elastic material constants of fiber composites vary along fiber directions. It is known that; the wood material behaves like a nonlinearly elastic composite structure under torsion loading. However, in addition to this phenomenon, it also exhibits visco- elastic properties. Transversely isotropic structure of wood is related to the natural growth of a tree. Annual rings of the wood form fairly regular concentric circles in nature, giving the wood cylindrically symmetric structure. Wood material enters the lightweight materials group with its composite structure. Therefore, the use of wood materials will take place between other light composite materials considered in aircraft engineering.
Coordinate dependent material elastic constants which were represented with mathematical equations, were studied analytically by scientists [1] -[4] . An extensive body of experimental data according to the variation of in-plane shear modulus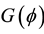 , and the variation of Young’s modulus
, and the variation of Young’s modulus 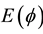 of plywood panels were gathered and analyzed, in this sense. The mathematical relations between elastic properties of fiber and matrix structure and the wood polymer elastic constants in micromechanical level were studied [5] . In the literature we have found out that, the simulation of wood nonlinearity was formulated as equivalent stresses and equivalent plastic strain relationships by using power functions [6] - [9] .
of plywood panels were gathered and analyzed, in this sense. The mathematical relations between elastic properties of fiber and matrix structure and the wood polymer elastic constants in micromechanical level were studied [5] . In the literature we have found out that, the simulation of wood nonlinearity was formulated as equivalent stresses and equivalent plastic strain relationships by using power functions [6] - [9] .
Fundamental works on wood compression were represented as continuous functions [10] [11] . Beside these, these researchers have used bilinear or tri-linear functions for the wood nonlinear modeling [12] - [17] . Generally, 2D analyses with plane-stress or plane-strain assumption were employed by most FE models for wood or wood composites and they were generally unable to completely describe the 3D stress fields.
Few attempts were found in the literature concerning with the 3D analysis of wood and associated constitutive models. In the literature survey, we haven’t found an accepted nonlinear constitutive model for wood that describes the change of elastic constants in 3D as the stiffness becomes nonlinear [7] [16] .
It is noteworthy that, “Japanese Iosipescu Shear Testing Method” standardized for fiber-reinforced plastics (FRP) was given in the American Society for Testing Material (ASTM) D5379. In this survey, radial and/or longitudinal plane shear behavior was mentioned.
The above mentioned test method was used in measuring the shearing properties of wood type materials [18] . The nonlinear material model presents the power functions which represent the stiffness change based on initial stiffness or stiffness of previous recurrences. Interestingly, typical nonlinearity of wood was observed under the compression loading and along with the shearing directions.
According to another study, in the modeling of the lateral buckling strength of large cross-section beam-co- lumns, the values of the shear modulii GLT and GLR should be known. Thereafter, their variation under creep can be easily defined. In the above mentioned study, power law and exponential law were adopted for creep testing on the wood-species and a linear-parabolic model was adopted for the short term behavior. Power and exponential laws have been chosen as creep functions due to their ease of handling properly in the numerical computation of the creep strain rates [19] .
In the literature, it is possible to find specific studies on the simulation of wood nonlinearity under shear and compression. The objective of one of these studies was developing a “3D finite element modeling” that corresponds to the wood material behavior [20] .
In the literature survey, researchers have focused on both theoretical and experimental studies that based on genetic optimization and optical metrology in order to obtain whole displacement fields of wood-based panels under bending loading. Tests were named as “Non-statically determined tests” because of the absence of unique analytical relations. In these studies, the developing complex stress fields were found as not only depending on boundary conditions, but also on constitutive equations [21] .
In order to obtain the balanced modulii in torsion (GJ) of wood-based composite materials, two finite element method (FEM) Fortran approaches (in displacement and stress) were proposed under the Saint Venant assumption. In this study, finite element analysis results were compared with the experimental values which were obtained from the torsion tests on specimens [22] .
The Norway spruce was analyzed numerically using the bilinear material law, and the experimental data are available in the literature. According to this study; as the rolling shear of RT plane has shown mostly nonlinearity, it is seldom observed on the LT plane. The results of analyses with modified bilinear parameters reflected good correspondence with the experimental findings. The parameters were found to be nearly equal to the Weibull statistical distributions [23] .
In the another study, the test which was named as “Arcan shear test” was used to investigate orthotropic shear modulus values of softwood Norway spruce. Video extensometer method was used in measuring the strain on the critical specimen section, and the determined moduli were evaluated by means of FEM calculations. In this study it was stated that, the 3-parameter Weibull distribution was the most appropriate method for the probabilistic description of the three orthotropic shear modulii of wood [24] .
In another similar publication; in which the Norway spruce was investigated again by means of the Arcan shear test, the data were obtained until failure occurs in each of the three orthotropic shear planes. In this latter study, the stress-strain curves were adapted to the linear, bilinear and Voce models [25] .
A new relationship to calculate the shear modulus ![]() in terms of off-axis modulus of elasticity
in terms of off-axis modulus of elasticity ![]() of orthotropic specimens such as wood-based panels was proposed. The verification of shear modulus transformation rules to obtain basic engineering constants that agrees with reliable test data and the anisotropic elasticity theory was performed [26] . The shear stress versus shear strain expressions of transversely isotropic cylindrical bar under torsion, having a finite length, was described in terms of partial differential equations [27] [28] . In the current study, two coordinate systems were used to define the coordinate dependent strain variations of pinewood specimens under torque, applied in z direction. The results which were obtained by performing pointwise incremental measurements, were illustrated as curves of point-wise shear stress
of orthotropic specimens such as wood-based panels was proposed. The verification of shear modulus transformation rules to obtain basic engineering constants that agrees with reliable test data and the anisotropic elasticity theory was performed [26] . The shear stress versus shear strain expressions of transversely isotropic cylindrical bar under torsion, having a finite length, was described in terms of partial differential equations [27] [28] . In the current study, two coordinate systems were used to define the coordinate dependent strain variations of pinewood specimens under torque, applied in z direction. The results which were obtained by performing pointwise incremental measurements, were illustrated as curves of point-wise shear stress ![]() vs. shear strain
vs. shear strain![]() , along the principal directions at the gauge locations. The torque loading was applied to the specimen in the
, along the principal directions at the gauge locations. The torque loading was applied to the specimen in the ![]() plane at one end, while the other end was fixed. The related data which was gathered from all these points was
plane at one end, while the other end was fixed. The related data which was gathered from all these points was
shown as separate curves for each test case. The purpose was to show the variations of the ![]() as func-
as func-
tions of ![]() [29] [30] . Consequently, these curves were formulated as empirical mathematical equations. In each test case, the coordinate dependent variations of the shear modulus functions
[29] [30] . Consequently, these curves were formulated as empirical mathematical equations. In each test case, the coordinate dependent variations of the shear modulus functions![]() ,
, ![]() and
and ![]() along the
along the![]() ,
, ![]() and
and ![]() directions, respectively, were generated on the circumferential surface of the tubular specimen.
directions, respectively, were generated on the circumferential surface of the tubular specimen.
2. Experiment and Method
Tubular pinewood specimens were used in this study (Figures 1(a)-(c)). The average moisture content of the material was measured and tabulated around 6% - 7% levels. Meanwhile, the geometry of the specimens were formed by taking fillet depths equal to the radius of the outer portion of the wood shaft (see Figure 1(c)). Thus, it became possible to minimize stress concentrations around specimen headings. The torsion load in Equation (1) was applied on the transverse plane (![]() plane, Figure 1(b)) which had a unit normal vector
plane, Figure 1(b)) which had a unit normal vector ![]() along the
along the ![]() direction.
direction.
![]() (1)
(1)
The measured coordinate dependent point-wise shear strain data ![]() generated by the applied torque
generated by the applied torque![]() .
.
All experiments were performed in room temperature by making use of uni-axial and tri-axial rosette gauges. These gauges were bonded onto the specimens at definite locations (Figure 1(a)). In order to minimize the deviations in the test results; these specimens were manufactured from a single tree trunk. The forming procedure was performed on the wood specimens in such a way that their fibers lay longitudinally parallel to the trunk. However, there were intrinsic structural differences stemming from the number and radii of annual rings in the part of the trunk from which the specimen was taken out. The experimental set-up was displayed as a schematic diagram in Figure 2. The torsion loading was applied by using TQSM-21 torsion testing machine [31] . Data was collected by employing a specialized units [32] - [34] . The set-up included torsion test machine and two different data acquisition systems. In this study, the data was simultaneously stored in terms of output voltage difference![]() . As a first step, the normal strain values were obtained by reading the voltage differences from the display of the unit, and as a second step, these normal strains were converted into shear strains by using Mohr’s circle [35] .
. As a first step, the normal strain values were obtained by reading the voltage differences from the display of the unit, and as a second step, these normal strains were converted into shear strains by using Mohr’s circle [35] .
3. Measurements
In the consideration of the resultant curves![]() , different failure stresses were established at the for-
, different failure stresses were established at the for-
ward and backward rotation directions. Directions of forward and backward torque loadings, ![]() or
or![]() , indicated the fiber angles [36] . Only the forward loading case was considered in the empirical formulation of this study. Results of the experimental studies were analyzed mainly in two steps. Firstly, specific locations
, indicated the fiber angles [36] . Only the forward loading case was considered in the empirical formulation of this study. Results of the experimental studies were analyzed mainly in two steps. Firstly, specific locations
were defined along the![]() ,
, ![]() ,
, ![]() directions on the specimens and shear stress versus strain
directions on the specimens and shear stress versus strain ![]() curves were obtained for each location.
curves were obtained for each location.
![]()
Figure 2. Schematic diagram of the experimental torsion test set-up with data acquisition systems, cables, tubular specimen with gauges on it. Additionally, sequence of the experimental operations were also shown.
Secondly, the variations of point-wise shear modulus values of each specimen were shown as shear modulii![]() ,
, ![]() ,
, ![]() versus
versus ![]() directions [28] . Subscripts of shear modulus,
directions [28] . Subscripts of shear modulus, ![]() represent the transverse surface; on which the torque was applied, On the other hand, circumferential surface is represented by using subscripts
represent the transverse surface; on which the torque was applied, On the other hand, circumferential surface is represented by using subscripts![]() . Strain gauges, on which measurements were taken, were installed along the z-axis (Fig- ure 1(a)). At the following step of the experiment; exponential and quadratic equations of the variations were tabulated. Measurements were performed by considering two reference coordinate systems in order to explain the wood specimen behavior: global cylindrical coordinate system
. Strain gauges, on which measurements were taken, were installed along the z-axis (Fig- ure 1(a)). At the following step of the experiment; exponential and quadratic equations of the variations were tabulated. Measurements were performed by considering two reference coordinate systems in order to explain the wood specimen behavior: global cylindrical coordinate system ![]() and local coordinate system (wood fiber arrangement based on principal material directions; 1, 2, 3) (Figure 1(a)). The local and global coordinate systems were used together for the definition of MA (measurement axis). MA served as a variable of wood fiber direction
and local coordinate system (wood fiber arrangement based on principal material directions; 1, 2, 3) (Figure 1(a)). The local and global coordinate systems were used together for the definition of MA (measurement axis). MA served as a variable of wood fiber direction![]() . The angular positions of the strain gauges on the circumferential surface relative to
. The angular positions of the strain gauges on the circumferential surface relative to ![]() -axis, were aligned with respect to maximum shear stress. The maximum shear stress was the stress formed around MA. These angular positions were denoted as MAA (Measurement Axis Angle) and they were taken as Equation (2).
-axis, were aligned with respect to maximum shear stress. The maximum shear stress was the stress formed around MA. These angular positions were denoted as MAA (Measurement Axis Angle) and they were taken as Equation (2).
![]() (2)
(2)
(Each MA lies on the 1-3 principal plane which corresponds to ![]() plane (Figure 1(b)). Measurement Axis Angle MAA is relatively different from the geometrical central axis angle
plane (Figure 1(b)). Measurement Axis Angle MAA is relatively different from the geometrical central axis angle![]() . MAA was defined on the 1-3 principal material plane which was attached on the surface of the cylinder. The first strain gauge was attached with
. MAA was defined on the 1-3 principal material plane which was attached on the surface of the cylinder. The first strain gauge was attached with ![]() angle in the principal material axis-1. All other gauges were also located along this direction (Fig- ure 1(a)). Application of gauges in
angle in the principal material axis-1. All other gauges were also located along this direction (Fig- ure 1(a)). Application of gauges in![]() ,
, ![]() ,
, ![]() ,
, ![]() locations were repeated in similar way. In the rest of the study, z-axis was rotated to be
locations were repeated in similar way. In the rest of the study, z-axis was rotated to be ![]() such that it coincided with MA.
such that it coincided with MA.
Invariants ![]() remain constant with respect to coordinate transformations. Stress and strain components were uncoupled along the principal directions for
remain constant with respect to coordinate transformations. Stress and strain components were uncoupled along the principal directions for ![]() and
and ![]() (Figure 1(b)). Only along the principal directions, principal stress and strain values of the isotropic materials coincided with the principal values of fiber composite materials on the Mohr’s circle [30] [37] [38] . Thus, it became easier to understand the behavior of the wood material under torsion and to compare it with that of the isotropic material. Accordingly, the shear modulus functions were derived along the MA directions for the corresponding principal stresses and strains. In literature, the shear modulus, shear strength, and principal strain angle were measured from the shear stress/ shear strain relation obtained by Iosipescu shear tests. Tests were conducted, and the validity of the in-plane shear tests was examined for the thin strips of western hemlock (Tsuga Heterophylla Sarg.) [39] . In this work, the torque value
(Figure 1(b)). Only along the principal directions, principal stress and strain values of the isotropic materials coincided with the principal values of fiber composite materials on the Mohr’s circle [30] [37] [38] . Thus, it became easier to understand the behavior of the wood material under torsion and to compare it with that of the isotropic material. Accordingly, the shear modulus functions were derived along the MA directions for the corresponding principal stresses and strains. In literature, the shear modulus, shear strength, and principal strain angle were measured from the shear stress/ shear strain relation obtained by Iosipescu shear tests. Tests were conducted, and the validity of the in-plane shear tests was examined for the thin strips of western hemlock (Tsuga Heterophylla Sarg.) [39] . In this work, the torque value ![]() as measured incrementally from the torsion testing machine. Variation of
as measured incrementally from the torsion testing machine. Variation of ![]() were plotted by using the inner or outer shear stresses
were plotted by using the inner or outer shear stresses ![]() and their corresponding principal shear strains. Consequently, shear modulus functions for the principal shear strains and corresponding shear stresses were expressed in terms of
and their corresponding principal shear strains. Consequently, shear modulus functions for the principal shear strains and corresponding shear stresses were expressed in terms of ![]() as in Equation (3):
as in Equation (3):
![]() (3)
(3)
Experimental results were discussed in the following section in detail.
4. Results and Discussion
Distributions of shear modulus functions and related empirical formulas were determined for pinewood. Beside this, average and equivalent mechanical properties of shear modulus values ![]() corresponding to the average shear stresses
corresponding to the average shear stresses ![]() for different types of wood (pine, oak, chestnut, hornbeam) were measured and results were listed in Table 1. These measurements were performed without using strain gauges and the related data was obtained from the second form of the nonlinear exact tri-linear curve
for different types of wood (pine, oak, chestnut, hornbeam) were measured and results were listed in Table 1. These measurements were performed without using strain gauges and the related data was obtained from the second form of the nonlinear exact tri-linear curve![]() .
.
In the application direction of torsion loading; since the resultant curves ![]() were affected, different failure values were formed. Applied loading directions
were affected, different failure values were formed. Applied loading directions ![]() or
or![]() , represent the backward and forward loadings of torque, respectively. Forward loading applications yield higher failure values than the backward ones. The empirical equations of
, represent the backward and forward loadings of torque, respectively. Forward loading applications yield higher failure values than the backward ones. The empirical equations of![]() ,
, ![]() and
and ![]() were expressed in terms of various functions and were listed in the Table 2. The descriptions of the results were explained according to the relative differences of slopes in shear stress-strain
were expressed in terms of various functions and were listed in the Table 2. The descriptions of the results were explained according to the relative differences of slopes in shear stress-strain ![]() and their corresponding
and their corresponding![]() ,
, ![]() ,
, ![]() versus
versus ![]() curves for forward loading applications. Figure 3 presents
curves for forward loading applications. Figure 3 presents ![]() (GPa) versus
(GPa) versus ![]() (degree) distribution of data obtained from six gauges at
(degree) distribution of data obtained from six gauges at ![]() for the tubular specimen. This distribution is obtained through the specified coordinates of MAA at the outer and/or inner surfaces of specimens (see Figures 1(a)-(c)).
for the tubular specimen. This distribution is obtained through the specified coordinates of MAA at the outer and/or inner surfaces of specimens (see Figures 1(a)-(c)).
In Figure 3, the outer and inner surface ![]() reactions due to the shear stress-strain distributions were formed in reverse orders at the measurement point where
reactions due to the shear stress-strain distributions were formed in reverse orders at the measurement point where ![]() is equal to
is equal to![]() . Through the circumferential direction,
. Through the circumferential direction, ![]() forms a convex curve at the inner surface and
forms a convex curve at the inner surface and ![]() forms a concave curve at the outer surface. Figure 4 presents
forms a concave curve at the outer surface. Figure 4 presents ![]() (GPa) versus
(GPa) versus ![]() (mm) distribution from four gauges at
(mm) distribution from four gauges at ![]() for the tubular specimen. Variation of function
for the tubular specimen. Variation of function ![]() shows parabolic distribution. It is concluded that
shows parabolic distribution. It is concluded that ![]() at the loaded end is bigger than
at the loaded end is bigger than ![]() at the fixed end. Figure 5 presents
at the fixed end. Figure 5 presents ![]() (GPa) versus
(GPa) versus ![]() (mm) distribution at
(mm) distribution at ![]() for the data obtained from six gauges at
for the data obtained from six gauges at![]() . It demonstrates dependency of
. It demonstrates dependency of ![]() (GPa) versus
(GPa) versus ![]() (mm) on the MA angles
(mm) on the MA angles![]() . In these
. In these
![]()
Table 1. Average shear modulus values of typical wood types obtained without using strain gauges![]() .
.
![]()
Table 2. Experimentally determined linear and nonlinear shear modulus functions of pinewood.
tests, gauges were located on both inner and outer surfaces with ![]() (see Figure 6). At these locations of
(see Figure 6). At these locations of![]() , the variations of
, the variations of ![]() from inner to outer surface decrease. Hence, it is concluded that:
from inner to outer surface decrease. Hence, it is concluded that:
1) ![]() (GPa) versus
(GPa) versus ![]() (mm) varies linearly along the circumferential surface. This is a consequence of
(mm) varies linearly along the circumferential surface. This is a consequence of ![]() values on the inner surface are being bigger than
values on the inner surface are being bigger than ![]() values on the outer surface.
values on the outer surface.
2) Shear stresses formed on the outer surface are smaller than the shear stresses formed on the inner surface because shear stresses on the inner surface accumulate densely and shear stresses on the outer surface do not accumulate that densely.
![]()
Figure 4. Two plots of ![]() (GPa) versus
(GPa) versus ![]() (mm) at z = 65, 157, 177, 200 mm.
(mm) at z = 65, 157, 177, 200 mm.
Empirical expressions of![]() ,
, ![]() and
and ![]() were obtained for tubular specimens by statistically evaluating the coefficients
were obtained for tubular specimens by statistically evaluating the coefficients ![]() from the related experimental data. These coefficients were tabulated in Table 3 in five groups (GPa) with their standard deviation (SY), coefficient of deviation (c.v.) and mean values (GPa) as follows:
from the related experimental data. These coefficients were tabulated in Table 3 in five groups (GPa) with their standard deviation (SY), coefficient of deviation (c.v.) and mean values (GPa) as follows:
1) First group coefficients of the linear and exponential ![]() functions were
functions were![]() ,
, ![]() and
and![]() ,
, ![]() respectively. 2) Second group coefficients of the parabolic and exponential
respectively. 2) Second group coefficients of the parabolic and exponential ![]() functions were obtained as
functions were obtained as![]() ,
, ![]() ,
, ![]() and
and![]() ,
, ![]() respectively. 3) Third group coefficients of the parabolic functions
respectively. 3) Third group coefficients of the parabolic functions ![]() on the inner surface of the tubular specimens were
on the inner surface of the tubular specimens were![]() ,
, ![]() ,
,![]() . Corresponding coefficients for the exponential function were calculated as
. Corresponding coefficients for the exponential function were calculated as![]() ,
,![]() . 4) Fourth group coefficients of the parabolic functions
. 4) Fourth group coefficients of the parabolic functions ![]() on the outer surface were
on the outer surface were![]() ,
, ![]() ,
,![]() . Coefficients for the exponential function were obtained as
. Coefficients for the exponential function were obtained as![]() ,
, ![]() , accordingly. 5) Fifth group coefficients of the parabolic functions
, accordingly. 5) Fifth group coefficients of the parabolic functions ![]() on the outer surface were obtained as
on the outer surface were obtained as![]() ,
, ![]() and
and![]() . Corresponding coefficients for the exponential function were determined as
. Corresponding coefficients for the exponential function were determined as![]() ,
, ![]() (Table 2).
(Table 2).
5. Conclusions
In this research study, variations of the shear modulus of transversely isotropic pinewood specimens under torsion were examined. The set of equations of shear modulus in ![]() and
and ![]() planes along the principal directions were formulated. All measurements were performed in terms of local coordinate system. As a continuation of this study for the future an extended experimental study is planned. In this future study it is suggested to calculate additional shear modulus functions and related coefficients by using different loading types on different wood species. As is known, the elastic constants’ matrix
planes along the principal directions were formulated. All measurements were performed in terms of local coordinate system. As a continuation of this study for the future an extended experimental study is planned. In this future study it is suggested to calculate additional shear modulus functions and related coefficients by using different loading types on different wood species. As is known, the elastic constants’ matrix ![]() appearing in the Hooke’s general law is used to define the elastic constants of materials. In this matrix, it is possible to identify these constants in the form of linear and nonlinear functions by replacing
appearing in the Hooke’s general law is used to define the elastic constants of materials. In this matrix, it is possible to identify these constants in the form of linear and nonlinear functions by replacing![]() ,
, ![]() and
and ![]() with
with![]() ,
, ![]() and
and ![]() for the pinewood (Pinus sylvestris L.) material.
for the pinewood (Pinus sylvestris L.) material.
Results were summarized below as follows:
1) In our study, we have shown that ![]() and
and ![]() can be written as
can be written as ![]() and
and ![]() and these functional values can be calculated by substituting the values of the normal strain components
and these functional values can be calculated by substituting the values of the normal strain components ![]() and the shear strain terms
and the shear strain terms ![]() into the Hooke’s general law (Equation (4)). The equations obtained by replacing linear and nonlinear shear modulus functions with unknown elastic constants, can be used in theoretical and numerical researches [28] .
into the Hooke’s general law (Equation (4)). The equations obtained by replacing linear and nonlinear shear modulus functions with unknown elastic constants, can be used in theoretical and numerical researches [28] .
![]() (4)
(4)
2) According to our study it is concluded that, ![]() values at
values at ![]() is equal to 200 mm are greater than the
is equal to 200 mm are greater than the ![]() values at
values at ![]() is equal to 70 mm. Similarly,
is equal to 70 mm. Similarly, ![]() values are smaller than the
values are smaller than the ![]() values, and,
values, and, ![]() values at
values at ![]() is equal to 200 mm are larger than
is equal to 200 mm are larger than ![]() values at
values at ![]() is equal to 70 mm.
is equal to 70 mm.
3) In our study it is also defined that, obtained shear modulus values along the 0˚ fibers are larger than the other two 45˚ and ![]() directed measurements performed with tri-axial rosette gauges. Results obtained from
directed measurements performed with tri-axial rosette gauges. Results obtained from
![]()
Table 3. Shear modulus linear/nonlinear functions including the statistical values of the coefficients (GPa).
measurements along the 0˚ oriented wood fibers, yield very small positive or negative shear strain values in general. Additionally, forward or backward loadings cause extension or contraction along the fibers and in turn, this generates positive or negative shear strains respectively.
4) The negative shear strains which develop at the measurement points as a consequence of forward loading applying can be explained by contraction of the material along the fibers. Thus, behavior of the shear strains are dependent both upon arrangement of the wood fibers and the load applying direction (Table 3).
5) According to the results of measurements along the MA directions using tri-axial rosette gauges, we have concluded that, the relative shear strain changes between 0˚ - 45˚ and 45˚ - 90˚ angles are not equal to each other. The difference of shear strains between the 0˚ - 45˚ directions is smaller than the directions between 45˚ - 90˚.
We recommend further additional experiments, in order to enhance the understanding of complex wood behavior under torsion loading. The stress accumulation phenomenon at the critical points along the wood fibers should be supported by further experimental studies in future and in our opinion this is especially important for the aircraft engineering area.
Acknowledgements
The authors would like to thank the Gazi University for financial support (BAP) (Grant Ref No: 6/2003-21).
NOTES
*Corresponding author.