1. Introduction
Consider the switched system
 (1)
(1)
where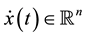 ,
,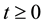 . In Equation (1), the matrix
. In Equation (1), the matrix 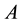 switches among
switches among 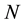 matrices
matrices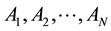 .
.
Switching signal 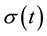 is piecewise continuous from the right function
is piecewise continuous from the right function 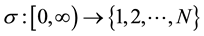 and the switching times are arbitrary. For the switched system (1) with initial condition
and the switching times are arbitrary. For the switched system (1) with initial condition 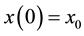 and with switching signal
and with switching signal  denotes the solution by
denotes the solution by .
.
Definition 1. The origin is uniformly asymptotically stable (UAS) for the system (1) if for every  there exists
there exists 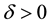 such that for every signal
such that for every signal 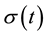 and initial state
and initial state 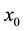 with
with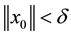 , the inequality
, the inequality ![]() is satisfied for all
is satisfied for all ![]() and uniformly on
and uniformly on ![]()
![]()
If all systems in (1) share a common quadratic Lyapunov function (CQLF) ![]() then the switched
then the switched
system is UAS (T denotes the transpose).
In this case there exists a common ![]() such that
such that
![]() (2)
(2)
and ![]() is called a common solution to the set of Lyapunov matrix inequalities (2).
is called a common solution to the set of Lyapunov matrix inequalities (2).
The problem of existence of common positive definite solution ![]() of (2) has been studied in a lot of works (see [1] -[9] and references therein). Numerical solution for common
of (2) has been studied in a lot of works (see [1] -[9] and references therein). Numerical solution for common ![]() via nondifferentiable convex optimization has been discussed in [10] .
via nondifferentiable convex optimization has been discussed in [10] .
In the first part of the paper, the problem of existence of CQLF is investigated by Kelley’s method. This method is applied when CQLF problem is treated as a convex optimization problem.
Second part of the paper is devoted to the following question:
Let ![]() be a compact, for
be a compact, for ![]() the matrix
the matrix ![]() is a real
is a real ![]() matrix. Is there a Hurwitz stable member (all eigenvalues lie in the open left half plane) in the family
matrix. Is there a Hurwitz stable member (all eigenvalues lie in the open left half plane) in the family
![]()
or equivalently is there ![]() such that
such that ![]() is stable? This problem is one of the hard and important problems in control theory (see [11] ). Numerical solution of this problem is considered in [12] . In this paper we reduce this problem to a non-convex optimization problem.
is stable? This problem is one of the hard and important problems in control theory (see [11] ). Numerical solution of this problem is considered in [12] . In this paper we reduce this problem to a non-convex optimization problem.
2. Common Quadratic Lyapunov Function
For the switched system
![]()
consider the problem of determination of CQLF ![]() where
where![]() . We are going to investigate it by Kelley’s cutting-plane method. This method gives new sufficient condition (Theorem 2) and new algorithm (Algorithm 1) which is more effective in comparison with the algorithm from [10] .
. We are going to investigate it by Kelley’s cutting-plane method. This method gives new sufficient condition (Theorem 2) and new algorithm (Algorithm 1) which is more effective in comparison with the algorithm from [10] .
Consider the problem of existence of a common ![]() such that
such that
![]() . (3)
. (3)
Let ![]() be
be ![]() and
and ![]() be an
be an ![]() symmetric matrix defined as
symmetric matrix defined as
![]()
Define
![]() (4)
(4)
If there exists ![]() such that
such that ![]() and
and ![]() then the matrix
then the matrix ![]() is required solution. This problem can be reduced to the minimization of a convex function under convex constraints.
is required solution. This problem can be reduced to the minimization of a convex function under convex constraints.
Consider the following convex minimization problem
![]() (5)
(5)
Let ![]() be a convex set and
be a convex set and ![]() be convex function. The vector
be convex function. The vector ![]() is said to be a subgradient of
is said to be a subgradient of ![]() at
at ![]() if for all
if for all ![]()
![]() .
.
The set of all subgradients of ![]() at
at ![]() is denoted by
is denoted by![]() . If
. If ![]() is an interior point of
is an interior point of ![]() then the set
then the set ![]() is nonempty and convex. The following proposition follows from nondifferentiable optimization theory.
is nonempty and convex. The following proposition follows from nondifferentiable optimization theory.
Proposition 1. Let ![]() be defined as
be defined as
![]() (6)
(6)
where ![]() is compact,
is compact, ![]() is continuous and differentiable in
is continuous and differentiable in![]() . Then
. Then
![]()
where ![]() is the set of all maximizing elements
is the set of all maximizing elements ![]() in (6), i.e.
in (6), i.e.
![]() .
.
If for a given ![]() the maximizing element is unique, i.e.
the maximizing element is unique, i.e. ![]() then
then ![]() is differentiable at
is differentiable at ![]() and its gradient is
and its gradient is
![]()
In the case of the Function (4)
![]()
If for the given ![]() the maximizing
the maximizing ![]() is unique and
is unique and ![]() is a simple eigenvalues, the differentiability of
is a simple eigenvalues, the differentiability of ![]() at the point
at the point ![]() is guaranteed [13] .
is guaranteed [13] .
We investigate problem (5) by Kelley’s cutting-plane method.
This method converts the problem (5) to the problem
![]() (7)
(7)
where![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Let ![]() be a starting point and
be a starting point and ![]() be
be ![]() distinct points.
distinct points.
At the ![]() th iteration, the cutting-plane algorithm solves the following LP problem
th iteration, the cutting-plane algorithm solves the following LP problem
![]() (8)
(8)
where ![]() denotes a subgradient of
denotes a subgradient of ![]() at
at![]() .
.
Let ![]() be the minimizer of the problem (8).
be the minimizer of the problem (8).
If ![]() satisfies the inequality
satisfies the inequality![]() , where
, where ![]() is a tolerance then
is a tolerance then ![]() is an approx-
is an approx-
imate solution of the problem (7).
Otherwise define ![]() as the index for the most negative
as the index for the most negative![]() , update the constraints in (8) by including the linear constraint
, update the constraints in (8) by including the linear constraint
![]()
and repeat the procedure.
Recall that our aim is to find ![]() such that
such that ![]() and
and![]() , but not the solution of the minimization problem (5), (7).
, but not the solution of the minimization problem (5), (7).
Theorem 2. If there exists ![]() such that
such that
![]()
where ![]() is the minimizer of the problem (8), then the matrix
is the minimizer of the problem (8), then the matrix ![]() is a common solution to (3).
is a common solution to (3).
Proof:
![]()
![]()
and by (5), ![]() is a common solution to (3).
is a common solution to (3).
For the problem (5), (7) Kelley’s method gives the following
Algorithm 1.
Step 1. Take an initial point![]() . Compute
. Compute ![]() and
and![]() . If
. If ![]() and
and ![]() stop; otherwise continue.
stop; otherwise continue.
Step 2. Determine ![]() by solving LP problem in (8). If
by solving LP problem in (8). If ![]() and
and ![]() then stop; otherwise continue. Set
then stop; otherwise continue. Set![]() , update the constraints in (8) and repeat the procedure.
, update the constraints in (8) and repeat the procedure.
Example 1. Consider the switched system
![]()
where
![]()
are Hurwitz stable matrices.
Choose the initial point![]() , then
, then
![]()
![]() ,
,![]() and
and![]()
We obtain ![]() by solving LP problem in (8). Calculations give the following Table 1, and
by solving LP problem in (8). Calculations give the following Table 1, and
![]()
Since ![]() and
and![]() ,
,
![]()
Table 1. Kelley’s algorithm for Example 1.
![]()
is a common positive definite solution for
![]()
3. Stable Member in a Polytope
This part is devoted to the following question: Given a matrix family ![]() where
where ![]() is a compact, is there a stable matrix in this family?
is a compact, is there a stable matrix in this family?
In [12] , a numerical algorithm has been proposed for a stable member in the affine matrix family![]() . In this algorithm the uncertainty vector
. In this algorithm the uncertainty vector ![]() varies in the whole space
varies in the whole space![]() . On the other hand we consider the case where
. On the other hand we consider the case where ![]() varies in a box
varies in a box ![]() and use the gradient algorithm for minimization of the nonconvex maximum eigenvalue function. By choosing appropriate step-size, we obtain the convergence.
and use the gradient algorithm for minimization of the nonconvex maximum eigenvalue function. By choosing appropriate step-size, we obtain the convergence.
Let ![]() be a basis for the subspace of
be a basis for the subspace of ![]() symmetric matrices and
symmetric matrices and
![]()
![]()
where![]() ,
,![]() .
.
Consider the problem
![]()
Theorem 3. There is a stable matrix in the family ![]() if and only if
if and only if ![]()
Proof:
![]()
![]()
![]()
By Lyapunov theorem, the matrix ![]() is stable.
is stable.
Example 2. Consider the family of matrices
![]()
where
![]()
For![]() ,
, ![]() is unstable. We apply the gradient algorithm to find a stable member in the family.
is unstable. We apply the gradient algorithm to find a stable member in the family.
Let ![]() and
and![]() . So
. So
![]()
Then
![]()
Maximum eigenvalue of this matrix and its corresponding unit eigenvector are
![]()
respectively. Gradient of the function ![]() at
at ![]() is
is
![]()
The first tencomponent of the vector ![]() should be on the ten dimensional unit sphere. Therefore
should be on the ten dimensional unit sphere. Therefore ![]() and
and
![]()
After 4 steps, we get
![]()
and![]() . Therefore
. Therefore ![]() is stable.
is stable.
4. Conclusion
Two important problems from control theory are considered: the existence of common quadratic Lyapunov functions for switched linear systems and the existence of a stable member in a matrix polytope. We obtain new conditions which give new effective computational algorithms.
NOTES
*Corresponding author.